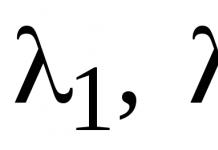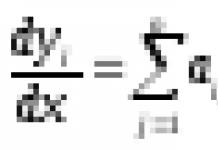Математическая статистика - Наука о том, как систематизировать и использовать статистические данные для научных и прикладных целей.

Математическая статистика в психологии

В психологии как науке математическая статистика применяется очень широко. С помощью тех или иных способов, например тестирования, разным особенностям поведения человека сопоставляются числа (шкалируются), и с этими числами уже работают методами математической статистики. После применения этих методов получаются новые данные, которые следует осмыслить.

Без применения математической статистики психология была бы довольно плоской и малоинформативной наукой, основанной на домыслах и спекуляциях (как это, например, имеет место быть в психоанализе). Разумеется, использование математической статистики не является "противоядием" против домыслов и спекуляций, однако предмет рассуждений становится значительно богаче.

Рассмотрим типичный и простой случай использования математической статистики. Допустим, кто-то провел исследование группы школьников. В числе прочих были найдены такие параметры, как экстраверсия-интроверсия и уровень интеллекта. Психолога-исследователя заинтересовало, а как связаны эти параметры между собой. Правда ли, что интроверты в среднем умнее экстравертов? Для этого группу испытуемых (выборку) можно поделить на две подгруппы: экстравертов и интровертов. Далее по каждой подгруппе находится среднее арифметическое по уровню интеллекта. Если, скажем, у интровертов в среднем IQ выше, значит, они умнее экстравертов. Это один подход. Другой может состоять в том, чтобы разделить испытуемых на подгруппу с высоким IQ (более 100) и низким (менее 100), а потом посчитать среднее по экстраверсии-интроверсии в каждой группе. Третий подход может состоять в том, чтобы вместо деления на подгруппы и высчитывания в них средних задействовать более сложный метод – корреляционный анализ. Все эти три методы по-разному, но покажут одну и ту же связь.

Математическая статистика позволяет делать интересные, иногда удивительные открытия. Продолжим наш гипотетический пример. Предположим, что психолог нашел парадоксальный результат, который противоречит с его прошлым опытом, знаниями. Скажем, он установил, что в одной школе экстраверты умнее интровертов, хотя во всех других школах было наоборот. Почему так? Дотошный психолог может начать свое расследование и установит, что, к примеру, это связано с тем, что в этой школе экстраверты ходят на факультатив по физике (потому что там «заводной учитель») и развивают свой интеллект, а интроверты ходят на факультатив по литературе (потому что там «душевный учитель»), где развивают другие качества своей души. Может ли, например, психоаналитик дойти до такого открытия? Крайне маловероятно.

В психологических исследованиях в расчет берутся не только такие чисто психологические параметры, как, скажем, интеллект, экстравертированность или тревожность. Могут использоваться и такие данные, как возраст, пол, уровень образования, рост, вес, физическая сила, политические взгляды, стаж работы и многое другое. Часто бывает, что именно без таких непсихологических показателей исследования оказываются неполными, малоинформативными. Также часто бывает, что представители других наук (например, социологии или биологии) тоже используют психологические параметры в своих исследованиях.

Математическая статистика позволяет много вещей:

Практические психологи в своей работе обычно ограничиваются нахождением средней арифметической, с разделением на подгруппы (как в примере выше). Ученые-психологи используют самый разнообразный арсенал методов математической статистики. Рассмотрим основные.

Нахождение средней арифметической

Самый банальный и простой метод. Показатели (например, рост испытуемых) складываются, затем делятся на число испытуемых. Несмотря на простоту, метод, конечно, очень информативный и наглядный. Наглядность – важное качество метода для практического психолога. Когда он представляет результаты своих исследований заказчику (например, директору школы), тот далеко не всегда способен понять сущность корреляционного или дисперсионного анализа. Разделение испытуемых на подгруппы по произвольному основанию усиливает потенциал средней арифметической, позволяя закрыть большинство потребностей исследователя.

Нахождение моды и медианы

Предположим, мы обследовали 1000 студентов – измеряли их рост с точностью до сантиметра. Эти данные заносили в таблицу. Если в таблице чаще всего встречается значение, скажем, 172 сантиметра, это и есть мода нашей выборки. Аналогичным, кстати, образом слово "мода" используется и в быту: если в этом сезоне чаще всего можно встретить шапочки красного цвета, значит это мода, хотя на долю этих шапочек может приходиться всего лишь 20 или 30 процентов.

В психологических исследованиях обычно мода находится где-то рядом со средней арифметической. Если мода 172 см, то и средняя будет около того. Чем больше выборка, тем ближе мода и среднее арифметическое.

Далее. Предположим, мы поделили своих студентов на две равные группы: в первой группе 500 низких студентов, во второй группе 500 высоких студентов. Значение роста, которое приходится на 500-го или 501-го студента и есть медиана . Медиана обычно тоже находится рядом со средней арифметической.

Выявление рассеяния значений

Как известно, средняя температура по больнице не так уж важна. И в хорошей больнице, где лечат хорошо, средняя температура может быть 36,6°C; и в плохой может быть такая же: просто у кого-то жар в 40 °C, а кто-то уже умер, и у него 18°C.

Самый простой способ оценить рассеяние выборки – найти ее размах (иначе – разброс). Если в нашей выборке самый низкий студент имеет рост 148 см, а самый высокий 205 см, значит размах выборки составит 205-148=57 см. Это величина важна в первую очередь для того, чтобы оценить, в каких рамках вообще меняется данный параметр.

Далее. Предположим такую ситуацию. Лет через двадцать по прихоти какого-нибудь богатого человека у него появятся дети-клоны. Ещё через двадцать лет они поступят в университет. И будет в университете выборка студентов объемом 1000 человек, из которых 998 имеют рост 177 см, один – 148 см, один – 205 см. По основным параметрам – средней арифметической, моде, медиане, размаху – эта выборка может не отличаться от другой выборки студентов (там будут такие же значения). Но при этом во второй (нормальной) выборке будет какое-то количество студентов с ростом 150-160 см, какое-то с ростом 180-190 см и т.д. Так что же, получается, что с точки зрения математической статистики эти группы одинаковые?

Одного взгляда на этот рисунок достаточно, чтобы понять, что группы различаются по рассеянию значений. Поэтому в статистике есть более точный инструмент для оценки рассеивания – дисперсия . Дисперсию исчисляют так: находят среднее арифметическое, потом для каждого случая находят отклонение от среднего, возводят это значение в квадрат, в конце делят на общее количество случаев. Из значения дисперсии легко получить стандартное отклонение : оно есть квадратный корень из дисперсии. Стандартное отклонение обозначает, что понятно, стандартное отклонение: то есть мера того, насколько в среднем значения вообще отклоняются.

Стандартное отклонение измеряется в тех же самых единицах, что и сам параметр. В первой нашей гипотетической группе, где почти все студенты одинаковы, стандартное отклонение будет крайне малым (менее 1 см). Во второй группе будет значительно больше – сантиметров 10-15. Если нам скажут, что средний рост студентов составляет 175 см при стандартном отклонении 12 см, мы будем знать, что большинство студентов (примерно 2/3) находится в диапазоне от 163 до 187 см.

t-критерий Стьюдента

Предположим, мы решили провести эксперимент такого рода. Мы взяли группу испытуемых. Перед началом эксперимента протестировали их, скажем, на уровень креативности. Далее они целый месяц занимались по часу в день рисованием. В конце эксперимента мы опять проверили их на уровень креативности. Был замечен результат, но довольно малый, и скептики стали нам заявлять, что уровень креативности не повысился, небольшое повышение средней арифметической это всего лишь случайность.

Для таких ситуаций придумали разные критерии. Один из них – наиболее популярный – это t-критерий Стьюдента. В числителе у него разница средних арифметических. В знаменателе – корень из суммы квадратов дисперсий (имеется в виду первый и второй случай тестирования). Чем больше разница между средними арифметическими, тем лучше (наш труд не остался напрасным), и чем меньше разброс значений в обоих случаях диагностики, тем тоже лучше: когда разброс значений больше, тогда и случайные колебания тоже больше.

Для применения данного критерия есть существенное ограничение – распределение показателей должно быть близко к так называемому нормальному (колоколообразному).

Существуют специальные критерии для определения степени нормальности распределения.

Корреляция

В психологии, как наверное ни в одной другой науке, любят находить коэффициенты корреляции. Существует несколько разных подходов, в том числе и для нормального, и для не нормального распределения. Все они показывают степень зависимости одного параметра от другого. Если один параметр (например, вес человека) сильно зависит от другого параметра (например, рост человека), тогда коэффициент корреляции будет близок к +1. Если зависимость обратная (например, чем человек выше, тем менее ловок он), тогда коэффициент корреляции будет стремиться к -1. Если зависимости нет (скажем, удачливость при игре в карты не зависит от роста человека), тогда коэффициент корреляции будет около 0.

Если взять группу испытуемых, зафиксировать их рост и вес, а потом результаты перенести на двухмерный график, то получится примерно следующая картина, которая свидетельствует о том, что корреляция положительная, примерно на уровне +0.5.

Факторный анализ

Наиболее, пожалуй, таинственный анализ. Некоторая загадочность его объясняется тем, что сам он предназначен для того, чтобы найти новый параметр, который многое объясняет, но при этом непосредственно в ходе эксперимента не исследовался. Как правило, в ходе факторного анализа находятся наиболее влиятельные параметры, от которых зависят более мелкие, частные.

Допустим, мы проводили исследование со школьниками. В числе прочих фиксировались следующие параметры: общая успеваемость, успеваемость по точным предметам, успеваемость по гуманитарным предметам, объем кратковременной памяти, объем и распределение внимания, активность мышления, пространственное воображение, общая осведомленность, общительность, тревожность. Если применить корреляционный анализ и составить так называемую матрицу корреляций (где отражена связь каждого параметра с каждым), то можно увидеть, что большинство этих параметров между собой хорошо коррелирует. Исключение составляет последние два, которые с другими связаны слабо. Уже глядя на эту матрицу можно предположить, что за большинством параметров стоит некий один общий (сверх-параметр), который на них на всех влияет. Мы проводим процедуру факторного анализа, и после этого в нашей матрице появляется еще один столбец – столбец без названия. Этот загадочный параметр очень хорошо коррелирует со всеми (кроме общительности и тревожности). После некоторого творческого раздумья психолог приходит к единственно возможной здесь интерпретации – загадочный параметр это есть интеллект. Он и влияет на все остальное, влияние его сильное, хотя и не стопроцентное.

Существуют методы факторного анализа, которые помогают выявить не один, а несколько факторов, которые влияют на другие параметры. Часто так бывает, конечно, что загадочный параметр оказывается не таким уж и загадочным, а полностью совпадает с одним из тех параметров, которые фиксировались. Но иногда бывает и так, что придется долго поломать голову прежде, чем удастся интерпретировать этот секретный фактор.

Факторный анализ применяется в основном учеными для глубокого понимания предмета исследования. При этом следует учитывать, что для точности результата необходимо довольно большое количество испытуемых: желательно, чтобы количество испытуемых в разы превышало количество параметров.

С помощью факторного анализа можно изучать качество психологических тестов. Если взять, например, какой-нибудь личностный опросник с несколькими параметрами, подвергнуть эти параметры факторному анализу, то может всплыть некий странный общий фактор, влияющий на все параметры. Значимого психологического смысла он может не иметь – это просто тенденция испытуемого отвечать так или иначе по формальному признаку (кто-то отвечает вдумчиво, кто-то склонен выбирать первые пункты из вариантов, кто-то последние). Большое влияние этого общего фактора может говорить о недостаточно качественной проработке заданий.

Литература

Ермолаев О. Ю. Математическая статистика для психологов: Учебник. - 2-е изд. испр. - М.: МПСИ, Флинта, 2003. - 336 с.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ.

Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретные и случайные непрерывные величины.

Дискретной называют величину, если она принимает счетное множество значений. (Пример: число пациентов на приеме у врача, число букв на странице, число молекул в заданном объеме).

Непрерывной называют величину, которая может принимать значения внутри некоторого интервала. (Пример: температура воздуха, масса тела, рост человека и т.д.)

Законом распределения случайной величины называется совокупность возможных значений этой величины и, соответствующих этим значениям, вероятностей (или частот встречаемости).

П р и м е р:

x	x 1	x 2	x 3	x 4	...	x n
p	р 1	р 2	р 3	р 4	...	p n

x	x 1	x 2	x 3	x 4	...	x n
m	m 1	m 2	m 3	m 4	...	m n

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.

Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины . Наиболее употребительные из них:

1 .Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:

2 .Дисперсия случайной величины:

3 .Среднее квадратичное отклонение :

Правило “ТРЕХ СИГМ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратичного отклонения

ЗАОН ГАУССА – НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Часто встречаются величины, распределенные по нормальному закону (закон Гаусса). Главная особенность : он является предельным законом, к которому приближаются другие законы распределения.

Случайная величина распределена по нормальному закону, если ее плотность вероятности имеет вид:

M(X) - математическое ожидание случайной величины;

s - среднее квадратичное отклонение.

Плотность вероятности (функция распределения) показывает, как меняется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой величины:

ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математическая статистика - раздел прикладной математики, непосредственно примыкающий к теории вероятностей. Основное отличие математической статистики от теории вероятностей состоит в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и числовых характеристик по результатам экспериментов.

Основными понятиями математической статистики являются:

1. Генеральная совокупность;

2. выборка;

3. вариационный ряд;

4. мода;

5. медиана;

6. процентиль,

7. полигон частот,

8. гистограмма.

Генеральная совокупность - большая статистическая совокупность, из которой отбирается часть объектов для исследования

(Пример: все население области, студенты вузов данного города и т.д.)

Выборка (выборочная совокупность) - множество объектов, отобранных из генеральной совокупности.

Вариационный ряд - статистическое распределение, состоящее из вариант (значений случайной величины) и соответствующих им частот.

Пример:

X,кг

m

x - значение случайной величины (масса девочек в возрасте 10 лет);

m - частота встречаемости.

Мода – значение случайной величины, которому соответствует наибольшая частота встречаемости. (В приведенном выше примере моде соответствует значение 24 кг, оно встречается чаще других: m = 20).

Медиана – значение случайной величины, которое делит распределение пополам: половина значений расположена правее медианы, половина (не больше) – левее.

Пример:

1, 1, 1, 1, 1. 1, 2, 2, 2, 3 , 3, 4, 4, 5, 5, 5, 5, 6, 6, 7 , 7, 7, 7, 7, 7, 8, 8, 8, 8, 8 , 8, 9, 9, 9, 10, 10, 10, 10, 10, 10

В примере мы наблюдаем 40 значений случайной величины. Все значения расположены в порядке возрастания с учетом частоты их встречаемости. Видно, что справа от выделенного значения 7 расположены 20 (половина) из 40 значений. Стало быть, 7 – это медиана.

Для характеристики разброса найдем значения, не выше которых оказалось 25 и 75% результатов измерения. Эти величины называются 25-м и 75-м процентилями . Если медиана делит распределение пополам, то 25-й и 75-й процентили отсекают от него по четвертушке. (Саму медиану, кстати, можно считать 50-м процентилем.) Как видно из примера, 25-й и 75-й процентили равны соответственно 3 и 8.

Используют дискретное (точечное) статистическое распределение инепрерывное (интервальное) статистическое распределение.

Для наглядности статистические распределения изображают графически в виде полигона частот или - гистограммы .

Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами (x 1 ,m 1 ), (x 2 ,m 2 ), ..., или для полигона относительных частот – с координатами (x 1 ,р * 1 ), (x 2 ,р * 2 ), ...(Рис.1).

m m i /n f(x)

Рис.1 Рис.2

Гистограмма частот - совокупность смежных прямоугольников, построенных на одной прямой линии (Рис.2), основания прямоугольников одинаковы и равны dx , а высоты равны отношению частоты к dx , или р * к dx (плотность вероятности).

Пример:

х, кг	2,7	2,8	2,9	3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2	4,3	4,4
m

Полигон частот

Отношение относительной частоты к ширине интервала носит название плотности вероятности f(x)=m i / n dx = p* i / dx

Пример построения гистограммы .

Воспользуемся данными предыдущего примера.

1. Расчет количества классовых интервалов

гдеn - число наблюдений. В нашем случае n = 100 . Следовательно:

2. Расчет ширины интервала dх :

,

3. Составление интервального ряда:

dх	2.7-2.9	2.9-3.1	3.1-3.3	3.3-3.5	3.5-3.7	3.7-3.9	3.9-4.1	4.1-4.3	4.3-4.5
m
f(x)	0.3	0.75	1.25	0.85	0.55	0.6	0.4	0.25	0.05

Гистограмма

Методы математической статистики

1. Введение

Математической статистикой называется наука, занимающаяся разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений.

В математической статистике можно выделить два направления: описательную статистику и индуктивную статистику (статистический вывод). Описательная статистика занимается накоплением, систематизацией и представлением опытных данных в удобной форме. Индуктивная статистика на основе этих данных позволяет сделать определенные выводы относительно объектов, о которых собраны данные, или оценки их параметров.

Типичными направлениями математической статистики являются:

1) теория выборок;

2) теория оценок;

3) проверка статистических гипотез;

4) регрессионный анализ;

5) дисперсионный анализ.

В основе математической статистики лежит ряд исходных понятий без которых невозможно изучение современных методов обработки опытных данных. В ряд первых из них можно поставить понятие генеральной совокупности и выборки.

При массовом промышленном производстве часто нужно без проверки каждого выпускаемого изделия установить, соответствует ли качество продукции стандартам. Так как количество выпускаемой продукции очень велико или проверка продукции связана с приведением ее в негодность, то проверяется небольшое количество изделий. На основе этой проверки нужно дать заключение о всей серии изделий. Конечно нельзя утверждать, что все транзисторы из партии в 1 млн. штук годны или негодны, проверив один из них. С другой стороны, поскольку процесс отбора образцов для испытаний и сами испытания могут оказаться длительными по времени и привести к большим затратам, то объем проверки изделий должен быть таким, чтобы он смог дать достоверное представление о всей партии изделий, будучи минимальных размеров. С этой целью введем ряд понятий.

Вся совокупность изучаемых объектов или экспериментальных данных называется генеральной совокупностью. Будем обозначать через N число объектов или количество данных, составляющих генеральную совокупность. Величину N называют объемом генеральной совокупности. Если N>>1, то есть N очень велико, то обычно считают N = ¥.

Случайной выборкой или просто выборкой называют часть генеральной совокупности, наугад отобранную из нее. Слово "наугад" означает, что вероятности выбора любого объекта из генеральной совокупности одинакова. Это важное предположение, однако, часто трудно это проверить на практике.

Объемом выборки называют число объектов или количество данных, составляющих выборку, и обозначают n . В дальнейшем будем считать, что элементам выборки можно приписать соответственно числовые значения х 1 , х 2 , ... х n . Например, в процессе контроля качества производимых биполярных транзисторов это могут быть измерения их коэффициента усиления по постоянному току.

2. Числовые характеристики выборки

2.1 Выборочное среднее

Для конкретной выборки объема n ее выборочное среднее

определяется соотношением

где х i – значение элементов выборки. Обычно требуется описать статистические свойства произвольных случайных выборок, а не одной из них. Это значит, что рассматривается математическая модель, которая предполагает достаточно большое количество выборок объема n. В этом случае элементы выборки рассматриваются как случайные величины Х i , принимающие значения х i с плотностью вероятностей f(x), являющейся плотностью вероятностей генеральной совокупности. Тогда выборочное среднее также является случайной величиной

равной

Как и ранее будем обозначать случайные величины прописными буквами, а значения случайных величин – строчными.

Среднее значение генеральной совокупности, из которой производится выборка, будем называть генеральным средним и обозначать m x . Можно ожидать, что если объем выборки значителен, то выборочное среднее не будет заметно отличаться от генерального среднего. Поскольку выборочное среднее является случайной величиной, для нее можно найти математическое ожидание:

Таким образом, математическое ожидание выборочного среднего равно генеральному среднему. В этом случае говорят, что выборочное среднее является несмещенной оценкой генерального среднего. В дальнейшем мы вернемся к этому термину. Так как выборочное среднее является случайной величиной, флуктуирующей вокруг генерального среднего, то желательно оценить эту флуктуацию с помощью дисперсии выборочного среднего. Рассмотрим выборку, объем которой n значительно меньше объема генеральной совокупности N (n << N). Предположим, что при формировании выборки характеристики генеральной совокупности не меняются, что эквивалентно предположению N = ¥. Тогда

Случайные величины Х i и X j (i¹j) можно считать независимыми, следовательно,

Подставим полученный результат в формулу для дисперсии:

где s 2 – дисперсия генеральной совокупности.

Из этой формулы следует, что с увеличением объема выборки флуктуации среднего выборочного около среднего генерального уменьшаются как s 2 /n. Проиллюстрируем сказанное примером. Пусть имеется случайный сигнал с математическим ожиданием и дисперсией соответственно равными m x = 10, s 2 = 9.

Отсчеты сигнала берутся в равноотстоящие моменты времени t 1 , t 2 , ... ,

X(t)
X 1

t 1 t 2 . . . t n t

Так как отсчеты являются случайными величинами, то будем их обозначать X(t 1), X(t 2), . . . , X(t n).

Определим количество отсчетов, чтобы среднее квадратическое отклонение оценки математического ожидания сигнала не превысило 1% его математического ожидания. Поскольку m x = 10, то нужно, чтобы

С другой стороны поэтому или Отсюда получаем, что n ³ 900 отсчетов.

2.2 Выборочная дисперсия

По выборочным данным важно знать не только выборочное среднее, но и разброс выборочных значений около выборочного среднего. Если выборочное среднее является оценкой генерального среднего, то выборочная дисперсия должна быть оценкой генеральной дисперсии. Выборочная дисперсия

для выборки, состоящей из случайных величин определяется следующим образом

Используя это представление выборочной дисперсии, найдем ее математическое ожидание

Математическая статистика является одним из основных разделов такой науки, как математика, и представляет собой отрасль, изучающую методы и правила обработки определенных данных. Иными словами, она исследует способы раскрытия закономерностей, которые свойственны большим совокупностям одинаковых объектов, основываясь на их выборочном обследовании.

Задача данного раздела состоит в построении методов оценки вероятности или принятии определенного решения о характере развивающихся событий, опираясь на полученные результаты. Для описания данных используются таблицы, диаграммы, а также корреляционные поля. применяются редко.

Математическая статистика используются в различных областях науки. К примеру, для экономики важно обрабатывать сведения об однородных совокупностях явлений и объектов. Ими могут являться изделия, выпускаемые промышленностью, персонал, данные о прибыли и т. д. В зависимости от математической природы результатов наблюдений, можно выделить статистику чисел, анализ функций и объектов нечисловой природы, многомерный анализ. Помимо этого, рассматривают общие и частные (связанные с восстановлением зависимостей, использованием классификаций, выборочными исследованиями) задачи.

Авторы некоторых учебников считают, что теория математической статистики является лишь разделом теории вероятности, другие - что это самостоятельная наука, имеющая собственные цели, задачи и методы. Однако в любом случае ее использование очень обширно.

Так, наиболее ярко математическая статистика применима в психологии. Ее использование позволит специалисту правильно обосновать найти зависимость между данными, обобщить их, избежать многих логических ошибок и многое другое. Нужно отметить, что измерить тот или иной психологический феномен или свойство личности без вычислительных процедур часто просто невозможно. Это говорит о том, что азы данной науки необходимы. Иными словами, ее можно назвать источником и базой теории вероятностей.

Метод исследования, который опирается на рассмотрение статистических данных, используется и в других областях. Однако сразу необходимо отметить, что его черты в применении к объектам, имеющим различную природу происхождения, всегда своеобразны. Поэтому объединять в одну науку физическую или не имеет смысла. Общие же черты данного метода сводятся к подсчету определенного числа объектов, которые входят в ту или иную группу, а также изучению распределения количественных признаков и применению теории вероятностей для получения тех или иных выводов.

Элементы математической статистики используются в таких областях, как физика, астрономия и т. д. Здесь могут рассматриваться значения характеристик и параметров, гипотезы о совпадении каких-либо характеристик в двух выборках, о симметрии распределения и многое другое.

Большую роль математическая статистика играет в проведении Их целью чаще всего является построение адекватных методов оценивания и проверка гипотез. В настоящее время огромное значение в данной науке имеют компьютерные технологии. Они позволяют не только значительно упростить процесс расчета, но и создать для размножения выборок или при изучении пригодности полученных результатов на практике.

В общем случае методы математической статистики помогают сделать два вывода: или принять искомое суждение о характере или свойствах изучаемых данных и их взаимосвязей, или доказать, что полученных результатов недостаточно для того, чтобы делать выводы.

Данным, полученным в результате эксперимента, свойственна изменчивость, которая может быть вызвана случайной ошибкой: погрешностью измерительного прибора, неоднородностью образцов и т.д. После проведения большого количества однородных данных экспериментатору необходимо их обработать для извлечения как можно более точной информации о рассматриваемой величине. Для обработки больших массивов данных измерений, наблюдений и т.п., которые могут быть получены при проведении эксперимента, удобно применять методы математической статистики .

Математическая статистика неразрывно связана с теорией вероятностей, но между этими науками есть существенное различие. Теория вероятностей использует уже известные распределения случайных величин , на основе которых рассчитываются вероятности событий, математическое ожидание т.д. Задача математической статистики – получить как можно более достоверную информацию о распределении случайной величины на основе экспериментальных данных.

Типичные направления математической статистики:

• теория выборок;
• теория оценок;
• проверка статистических гипотез;
• регрессионный анализ;
• дисперсионный анализ.

Методы математической статистики

Методы оценки и проверки гипотез основываются на вероятностных и гиперслучайных моделях происхождения данных.

Математическая статистика оценивает параметры и функции от них, которые представляют важные характеристики распределений (медиану, математическое ожидание, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используются точечные и интервальные оценки.

Современная математическая статистика содержит большой раздел – статистический последовательный анализ , в котором допускается формирование массива наблюдений по одному массиву.

Математическая статистика также содержит общую теорию проверки гипотез и большое количество методов для проверки конкретных гипотез (например, о симметрии распределения, о значениях параметров и характеристик, о согласии эмпирической функции распределения с заданной функцией распределения, гипотеза проверки однородности (совпадение характеристик или функций распределения в двух выборках) и др.).

Проведением выборочных обследований , связанных с построением адекватных методов оценки и проверки гипотез, со свойствами разных схем организации выборок, занимается раздел математической статистики, имеющий большое значение. Методы математической статистики непосредственно использует следующие основные понятия.

Выборка

Определение 1

Выборкой называются данные, которые получены при проведении эксперимента.

Например, результаты дальности полета пули при выстреле одного и того же или группы однотипных орудий.

Эмпирическая функция распределения

Замечание 1

Функция распределения дает возможность выразить все важнейшие характеристики случайной величины.

В математической стаитистике существует понятие теоретической (заранее не известной) и эмпирической функции распределения.

Эмпирическая функция определяется по данным опыта (эмпирические данные), т.е. по выборке.

Гистограмма

Гистограммы используются для наглядного, но довольно приближенного, представления о неизвестном распределении.

Гистограмма представляет собой графическое изображение распределения данных.

Для получения качественной гистограммы придерживаются следующих правил :

• Количество элементов выборки должно быть существенно меньше объема выборки.
• Интервалы разбиения должны содержать достаточное число элементов выборки.

Если выборка очень большая зачастую интервал элементов выборки разбивают на одинаковые части.

Выборочное среднее и выборочная дисперсия

С помощью данных понятий можно получить оценку необходимых числовых характеристик неизвестного распределения, не прибегая к построению функции распределения, гистограммы и т.п.