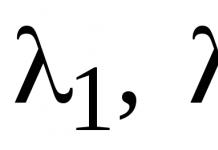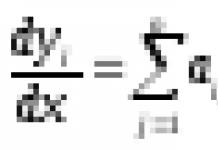Преобразование декартовых прямоугольных систем координат. Преобразование декартовой прямоугольной системы координат на плоскости

Пусть на плоскости заданы две произвольные декартовы прямоугольные системы координат. Первая определяется началом О и базисными векторамиi j , вторая – центром О’ и базисными векторами i ’ j ’ .

Поставим цель выразить координаты x y некоторой точки М относительно первой системы координат через x ’ и y ’ – координаты той же точки относительно второй системы.

Заметим, что

Обозначим координаты точки О’ относительно первой системы через a и b:

Разложим векторы i ’ и j ’ по базису i j :

(*)

Кроме того, имеем:
. Введем сюда разложения векторов по базисуi ’ j ’ :

отсюда

Можно сделать вывод: каковы бы ни были две произвольных декартовы системы на плоскости, координаты любой точки плоскости относительно первой системы являются линейными функциями координат той же точки относительно второй системы.

Умножим скалярно уравнения (*) сначала на i , затем на j :

Обозначим через угол между векторами i и i ’ . Система координат i j может быть совмещена с системой i ’ j ’ путем параллельного переноса и последующего поворота на угол . Но здесь возможен и дугой вариант: угол между базисными векторами i i ’ также , а угол между базисными векторами j ’ j ’ равен  - . Эти системы нельзя совместить параллельным переносом и поворотом. Необходимо еще и изменить направление оси у на противоположное.

Из формулы (**) получаем в первом случае:

Во втором случае

Формулы преобразования имеют вид:

Второй случай мы рассматривать не будем. Условимся считать обе системы правыми.

Т.е. вывод: каковы бы ни были две правые системы координат, первая из них может быть совмещена со второй путем параллельного переноса и последующего поворота вокруг начала на некоторый угол .

Формулы параллельного переноса:

Формулы поворота осей:

Обратные преобразования:

Преобразование декартовых прямоугольных координат в пространстве.

В пространстве, рассуждая аналогичным образом, можно записать:

(***)

И для координат получить:

(****)

Итак, каковы бы ни были две произвольные системы координат в пространстве, координаты x y z некоторой точки относительно первой системы являются линейными функциями координат x ’ y ’ z ’ этой же точки относительно второй системы координат.

Умножая каждое из равенств (***) скалярно на i ’ j ’ k ’ получаем:

Выясним геометрический смысл формул преобразования (****). Для этого предположим, что обе системы имеют общее начало:a = b = c = 0 .

Введем в рассмотрение три угла, полностью характеризующих расположение осей второй системы относительно первой.

Первый угол – образован осью х и осью u, являющейся пересечением плоскостей xOy и x’Oy’. Направление угла – кратчайший поворот от оси x к y. Обозначим угол через . Второй угол  – это не превосходящий  угол между осями Oz и Oz’. Наконец, третий угол  – это угол между осью u и Ox’, отсчитываемый от оси u в направлении кратчайшего поворота от Ox’ к Oy’. Эти углы называются углами Эйлера.

Преобразование первой системы во вторую можно представить в виде последовательного проведения трех поворотов: на угол  относительно оси Oz; на угол  относительно оси Ox’; и на угол  относительно оси Oz’.

Числа  ij можно выразить через углы Эйлера. Эти формулы мы записывать не будем из-за громоздкости.

Само преобразование представляет собой суперпозицию параллельного переноса и трех проводимых последовательных поворотов на углы Эйлера.

Все эти рассуждения можно провести и для случая, когда обе системы левые, или разной ориентации.

Если имеем две произвольные системы, то, вообще говоря, можно их совместить путем параллельного переноса и одного поворота в пространстве вокруг некоторой оси. Искать ее не будем.

Глава 1. Дополнение. Преобразование декартовых прямоугольных координат на плоскости и в пространстве. Специальные системы координат на плоскости и в пространстве.

Правила построения систем координат на плоскости и в пространстве рассмотрены в основной части Главы 1. Были отмечены удобства применения прямоугольных систем координат. При практическом использовании средств аналитической геометрии часто возникает необходимость преобразовать принятую систему координат. Обычно это диктуется соображениями удобства: упрощаются геометрические образы, нагляднее становятся аналитические модели и используемые при вычислениях алгебраические выражения.

Построение и использование специальных систем координат: полярных, цилиндрических и сферических диктуется геометрическим смыслом решаемой задачи. Моделирование при помощи специальных систем координат часто облегчают разработку и использование аналитических моделей при решении практических задач.

Результаты, полученные в Дополнении Главы 1, будут использоваться в линейной алгебре, большая часть – в математическом анализе и в физике.

Преобразование декартовых прямоугольных координат на плоскости и в пространстве.

При рассмотрении задачи построения системы координат на плоскости и в пространстве отмечалось, что систему координат образуют пересекающиеся в одной точке числовые оси: на плоскости требуются две оси, в пространстве – три. В связи с построением аналитических моделей векторов, введением операции скалярного произведения векторов и решением задач геометрического содержания было показано, что применение прямоугольных систем координат наиболее предпочтительно.

Если рассматривать задачу преобразования конкретной системы координат абстрактно, то в общем случае можно было бы допускать произвольное перемещение в заданном пространстве осей координат с правом произвольного переименования осей.

Мы будем исходить из первичного понятия системы отсчета , принятого в физике. Наблюдая движение тел, было обнаружено, что движение изолированного тела не может быть определено само по себе. Нужно иметь ещё хотя бы одно тело, относительно которого наблюдается движение, то есть изменение его относительного положения. Для получения аналитических моделей, законов, движения с этим вторым телом, как с системой отсчёта, связали систему координат, причём так, что система координат представляла собой твёрдое тело !

Так как произвольное перемещение твёрдого тела из одной точки пространства в другую может быть представлено двумя независимыми движениями: поступательное и вращательное, то варианты преобразования системы координат ограничили двумя движениями:

1). Параллельный перенос: следим только за одной точкой – точкой .

2). Вращение осей системы координат относительно точки : как твёрдого тела.

Преобразование декартовых прямоугольных координат на плоскости .

Пусть имеем на плоскости системы координат: , и . Система координат получается параллельным переносом системы . Система координат получается вращением системы на угол , причём за положительное направление вращение принято вращение оси против часовой стрелки.

Определим для принятых систем координат базисные векторы. Так как система получена параллельным переносом системы , то для обеих этих систем примем базисные векторы: , причём единичные и совпадающие по направлению с осями координат , , соответственно. Для системы в качестве базисных векторов примем единичные векторы , совпадающие по направлению с осями , .

Пусть задана система координат и в ней определена точка = . Будем считать, что перед преобразованием имеем совпадающие системы координат и . Применим к системе координат параллельный перенос, определяемый вектором . Требуется определить преобразование координат точки . Воспользуемся векторным равенством: = + , или:

Проиллюстрируем преобразование параллельного переноса известным в элементарной алгебре примером.

Пример Д –1 : Задано уравнение параболы: = = . Привести уравнение этой параболы к простейшей форме.

Решение :

1). Воспользуемся приёмом выделения полного квадрата : = , которое легко представить в виде: –3 = .

2). Применим преобразование координат – параллельный перенос : = . После этого уравнение параболы принимает вид: . Это преобразование в алгебре определяют так: парабола = получена смещением простейшей параболы вправо на 2, и вверх на 3 единицы.

Ответ: простейшая форма параболы: .

Пусть задана система координат и в ней определена точка = . Будем считать, что перед преобразованием имеем совпадающие системы координат и . Применим к системе координат преобразование вращения так, что относительно исходного своего положения, то есть относительно системы оказывается повёрнутой на угол . Требуется определить преобразование координат точки = . Запишем вектор в системах координат и : = . (2) =1. Из теории линий второго порядка следует, что получено простейшее (каноническое!) уравнение эллипса.

Ответ: простейшая форма заданной линии: =1 – каноническое уравнение эллипса.

1) Переход от одной декартовой прямоугольной системы координат на плоскости к другой декартовой прямоугольной системе с той же ориентацией и с тем же началом координат.

Предположим, что на плоскости введены две декартовы прямоугольные системы координат хОу и с общим началом координат О , имеющие одинаковую ориентацию (рис. 145). Обозначим единичные векторы осей Ох и Оу соответственно через и , а единичные векторы осей и через и . Наконец пусть - угол от оси Ох до оси . Пусть х и у – координаты произвольной точки М в системе хОу , а и - координаты той же точки М в системе .

Так как угол от оси Ох до вектора равен , то координаты вектора

Угол от оси Ох до вектора равен ; поэтому координаты вектора равны .

Формулы (3) § 97 принимают вид

Матрица перехода от одной декартовой хОу прямоугольной системы координат к другой прямоугольной системе с той же ориентацией имеет вид

Матрица называется ортогональной, если сумма квадратов элементов, расположенных в каждом столбце, равна 1, а сумма произведений соответствующих элементов разных столбцов равна нулю, т.е. если

Таким образом, матрица (2) перехода от одной прямоугольной системы координат к другой прямоугольной системе с той же ориентацией ортогональная. Отметим ещё, что определитель этой матрицы равен +1:

Обратно, если задана ортогональная матрица (3) с определителем, равным +1, и на плоскости введена декартова прямоугольная система координат хОу , то в силу соотношений (4) векторы и единичные и взаимно перпендикулярные, следовательно, координаты вектора в системе хОу равны и , где - угол от вектора до вектора , а так как вектор единичный и получим из вектора поворотом на , то либо , либо .

Вторая возможность исключается, так как если бы мы имели , то а нам дано, что .

Значит, , и матрица А имеет вид

т.е. является матрицей перехода от одной прямоугольной системы координат хОу к другой прямоугольной системе , имеющей ту же ориентацию, причем угол .

2. Переход от одной декартовой прямоугольной системы координат на плоскости к другой декартовой прямоугольной системе с противоположной ориентацией и с тем же началом координат.

Пусть на плоскости введены две декартовы прямоугольные системы координат хОу и с общим начало координат О , но имеющие противоположную ориентацию обозначим угол от оси Ох до оси через (ориентацию плоскости зададим системой хОу ).

Так как угол от оси Ох до вектора равен , то координаты вектора равны:

Теперь угол от вектора до вектора равен (рис. 146), поэтому угол от оси Ох до вектора равен (по теореме Шаля для углов) и поэтому координаты вектора равны:

И формулы (3) § 97 принимают вид

Матрица перехода

ортогональная, но ее определитель равен –1 . (7)

Обратно, любая ортогональная матрица с определителем, равным –1, задает преобразование одной прямоугольной системы координат на плоскости в другую прямоугольную систему с тем же началом, но противоположной ориентации. Итак, если две декартовы прямоугольные системы координат хОу и имеют общее начало, то

где х , у – координаты любой точки в системе хОу ; и - координаты той же точки в системе , а

ортогональная матрица.

Обратно, если

произвольная ортогональная матрица, то соотношениями

выражается преобразование декартовой прямоугольной системы координат в декартовую прямоугольную систему с тем же началом координат; - координаты в системе хОу единичного вектора , дающего положительное направление оси ; - координаты в системе хОу единичного вектора , дающего положительное направление оси .

системы координат хОу и имеют одинаковую ориентацию, а в случае - противоположную.

3. Общее преобразование одной декартовой прямоугольной системы координат на плоскости в другую прямоугольную систему.

На основании пунктов 1) и 2) этого параграфа, а также на основании § 96 заключаем, что если на плоскости введены прямоугольные системы координат хОу и , то координаты х и у произвольной точки М плоскости в системе хОу с координатами и той же точки М в системе связаны соотношениями- координаты начала системы координат в системе хОу .

Заметим, что старые и новые координаты х , у и , вектора при общем преобразовании декартовой прямоугольной системы координат связаны соотношениями

в случае, если системы хОу и имеют одинаковую ориентацию и соотношениями

в случае, если эти системы имеют противоположную ориентацию, или же в виде

ортогональная матрица. Преобразования (10) и (11) называются ортогональными.