Решение систем линейных алгебраических уравнений (СЛАУ), несомненно, является важнейшей темой курса линейной алгебры. Огромное количество задач из всех разделов математики сводится к решению систем линейных уравнений. Этими факторами объясняется причина создания данной статьи. Материал статьи подобран и структурирован так, что с его помощью Вы сможете
- подобрать оптимальный метод решения Вашей системы линейных алгебраических уравнений,
- изучить теорию выбранного метода,
- решить Вашу систему линейных уравнений, рассмотрев подробно разобранные решения характерных примеров и задач.
Краткое описание материала статьи.
Сначала дадим все необходимые определения, понятия и введем обозначения.
Далее рассмотрим методы решения систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных переменных и которые имеют единственное решение. Во-первых, остановимся на методе Крамера, во-вторых, покажем матричный метод решения таких систем уравнений, в-третьих, разберем метод Гаусса (метод последовательного исключения неизвестных переменных). Для закрепления теории обязательно решим несколько СЛАУ различными способами.
После этого перейдем к решению систем линейных алгебраических уравнений общего вида, в которых число уравнений не совпадает с числом неизвестных переменных или основная матрица системы является вырожденной. Сформулируем теорему Кронекера - Капелли, которая позволяет установить совместность СЛАУ. Разберем решение систем (в случае их совместности) с помощью понятия базисного минора матрицы. Также рассмотрим метод Гаусса и подробно опишем решения примеров.
Обязательно остановимся на структуре общего решения однородных и неоднородных систем линейных алгебраических уравнений. Дадим понятие фундаментальной системы решений и покажем, как записывается общее решение СЛАУ с помощью векторов фундаментальной системы решений. Для лучшего понимания разберем несколько примеров.
В заключении рассмотрим системы уравнений, сводящиеся к линейным, а также различные задачи, при решении которых возникают СЛАУ.
Навигация по странице.
Определения, понятия, обозначения.
Будем рассматривать системы из p
линейных алгебраических уравнений с n
неизвестными переменными (p
может быть равно n
) вида
Неизвестные переменные, - коэффициенты (некоторые действительные или комплексные числа), - свободные члены (также действительные или комплексные числа).
Такую форму записи СЛАУ называют координатной .
В матричной форме
записи эта система уравнений имеет вид ,
где 
- основная матрица системы, - матрица-столбец неизвестных переменных, - матрица-столбец свободных членов.
Если к матрице А
добавить в качестве (n+1)-ого
столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу
системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т
, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,
Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных , обращающий все уравнения системы в тождества. Матричное уравнение при данных значениях неизвестных переменных также обращается в тождество .
Если система уравнений имеет хотя бы одно решение, то она называется совместной .
Если система уравнений решений не имеет, то она называется несовместной .
Если СЛАУ имеет единственное решение, то ее называют определенной ; если решений больше одного, то – неопределенной .
Если свободные члены всех уравнений системы равны нулю 
, то система называется однородной
, в противном случае – неоднородной
.
Решение элементарных систем линейных алгебраических уравнений.
Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю, то такие СЛАУ будем называть элементарными . Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.
Такие СЛАУ мы начинали изучать в средней школе. При их решении мы брали какое-нибудь одно уравнение, выражали одну неизвестную переменную через другие и подставляли ее в оставшиеся уравнения, следом брали следующее уравнение, выражали следующую неизвестную переменную и подставляли в другие уравнения и так далее. Или пользовались методом сложения, то есть, складывали два или более уравнений, чтобы исключить некоторые неизвестные переменные. Не будем подробно останавливаться на этих методах, так как они по сути являются модификациями метода Гаусса.
Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса. Разберем их.
Решение систем линейных уравнений методом Крамера.
Пусть нам требуется решить систему линейных алгебраических уравнений
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .
Пусть - определитель основной матрицы системы, а 
- определители матриц, которые получаются из А
заменой 1-ого, 2-ого, …, n-ого
столбца соответственно на столбец свободных членов:
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как 
. Так находится решение системы линейных алгебраических уравнений методом Крамера.
Пример.
Методом Крамера 
.
Решение.
Основная матрица системы имеет вид 
. Вычислим ее определитель (при необходимости смотрите статью ):
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Составим и вычислим необходимые определители 
(определитель получаем, заменив в матрице А
первый столбец на столбец свободных членов , определитель - заменив второй столбец на столбец свободных членов, - заменив третий столбец матрицы А
на столбец свободных членов):
Находим неизвестные переменные по формулам 
:
Ответ:
Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрица A имеет размерность n на n и ее определитель отличен от нуля.
Так как , то матрица А – обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных . Так мы получили решение системы линейных алгебраических уравнений матричным методом.
Пример.
Решите систему линейных уравнений матричным методом.
Решение.
Перепишем систему уравнений в матричной форме:
Так как
то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как 
.
Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы А
(при необходимости смотрите статью ):
Осталось вычислить - матрицу неизвестных переменных, умножив обратную матрицу 
на матрицу-столбец свободных членов (при необходимости смотрите статью ):
Ответ:
или в другой записи x 1 = 4, x 2 = 0, x 3 = -1
.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из n
линейных уравнений с n
неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находится x n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1
из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому
уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а 
.
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому
уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а 
. Таким образом, переменная x 2
исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3
, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.
Пример.
Решите систему линейных уравнений методом Гаусса.
Решение.
Исключим неизвестную переменную x 1
из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на и на соответственно:
Теперь из третьего уравнения исключим x 2
, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x 3
:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
X 1 = 4, x 2 = 0, x 3 = -1 .
Решение систем линейных алгебраических уравнений общего вида.
В общем случае число уравнений системы p
не совпадает с числом неизвестных переменных n
:
Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.
Теорема Кронекера – Капелли.
Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли
:
для того, чтобы система из p
уравнений с n
неизвестными (p
может быть равно n
) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть, Rank(A)=Rank(T)
.
Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.
Пример.
Выясните, имеет ли система линейных уравнений 
решения.
Решение.
. Воспользуемся методом окаймляющих миноров. Минор второго порядка 
отличен от нуля. Переберем окаймляющие его миноры третьего порядка:
Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.
В свою очередь ранг расширенной матрицы 
равен трем, так как минор третьего порядка
отличен от нуля.
Таким образом, Rang(A) , следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.
Ответ:
Система решений не имеет.
Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.
А как же находить решение СЛАУ, если установлена ее совместность?
Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.
Минор наивысшего порядка матрицы А , отличный от нуля, называется базисным .
Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы А базисных миноров может быть несколько, один базисный минор есть всегда.
Для примера рассмотрим матрицу 
.
Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.
Базисными являются следующие миноры второго порядка, так как они отличны от нуля
Миноры 
базисными не являются, так как равны нулю.
Теорема о ранге матрицы.
Если ранг матрицы порядка p на n равен r , то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.
Что нам дает теорема о ранге матрицы?
Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r ), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).
В итоге, после отбрасывания излишних уравнений системы, возможны два случая.
Если число уравнений r в полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.
Пример.
.
Решение.
Ранг основной матрицы системы 
равен двум, так как минор второго порядка 
отличен от нуля. Ранг расширенной матрицы 
также равен двум, так как единственный минор третьего порядка равен нулю
а рассмотренный выше минор второго порядка отличен от нуля. На основании теоремы Кронекера – Капелли можно утверждать совместность исходной системы линейных уравнений, так как Rank(A)=Rank(T)=2
.
В качестве базисного минора возьмем . Его образуют коэффициенты первого и второго уравнений:
Третье уравнение системы не участвует в образовании базисного минора, поэтому исключим его из системы на основании теоремы о ранге матрицы:
Так мы получили элементарную систему линейных алгебраических уравнений. Решим ее методом Крамера:
Ответ:
x 1 = 1, x 2 = 2 .
Если число уравнений r в полученной СЛАУ меньше числа неизвестных переменных n , то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.
Неизвестные переменные (их r штук), оставшиеся в левых частях уравнений, называются основными .
Неизвестные переменные (их n - r штук), которые оказались в правых частях, называются свободными .
Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом r основных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.
Разберем на примере.
Пример.
Решите систему линейных алгебраических уравнений 
.
Решение.
Найдем ранг основной матрицы системы 
методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем a 1 1 = 1
. Начнем поиск ненулевого минора второго порядка, окаймляющего данный минор:
Так мы нашли ненулевой минор второго порядка. Начнем поиск ненулевого окаймляющего минора третьего порядка:
Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.
Найденный ненулевой минор третьего порядка возьмем в качестве базисного.
Для наглядности покажем элементы, образующие базисный минор:
Оставляем в левой части уравнений системы слагаемые, участвующие в базисном миноре, остальные переносим с противоположными знаками в правые части:
Придадим свободным неизвестным переменным x 2
и x 5
произвольные значения, то есть, примем 
, где - произвольные числа. При этом СЛАУ примет вид
Полученную элементарную систему линейных алгебраических уравнений решим методом Крамера:
Следовательно, .
В ответе не забываем указать свободные неизвестные переменные.
Ответ:
Где - произвольные числа.
Подведем итог.
Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.
Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.
Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.
Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.
Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
Методом Гаусса можно решать системы линейных алгебраических уравнений любого вида без предварительного их исследования на совместность. Процесс последовательного исключения неизвестных переменных позволяет сделать вывод как о совместности, так и о несовместности СЛАУ, а в случае существования решения дает возможность отыскать его.
С точки зрения вычислительной работы метод Гаусса является предпочтительным.
Смотрите его подробное описание и разобранные примеры в статье метод Гаусса для решения систем линейных алгебраических уравнений общего вида .
Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
В этом разделе речь пойдет о совместных однородных и неоднородных системах линейных алгебраических уравнений, имеющих бесконечное множество решений.
Разберемся сначала с однородными системами.
Фундаментальной системой решений однородной системы из p линейных алгебраических уравнений с n неизвестными переменными называют совокупность (n – r) линейно независимых решений этой системы, где r – порядок базисного минора основной матрицы системы.
Если обозначить линейно независимые решения однородной СЛАУ как X (1) , X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) – это матрицы столбцы размерности n на 1 ), то общее решение этой однородной системы представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами С 1 , С 2 , …, С (n-r) , то есть, .
Что обозначает термин общее решение однородной системы линейных алгебраических уравнений (орослау)?
Смысл прост: формула задает все возможные решения исходной СЛАУ, другими словами, взяв любой набор значений произвольных постоянных С 1 , С 2 , …, С (n-r) , по формуле мы получим одно из решений исходной однородной СЛАУ.
Таким образом, если мы найдем фундаментальную систему решений, то мы сможем задать все решения этой однородной СЛАУ как .
Покажем процесс построения фундаментальной системы решений однородной СЛАУ.
Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения 1,0,0,…,0 и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, например, методом Крамера. Так будет получено X (1) - первое решение фундаментальной системы. Если придать свободным неизвестным значения 0,1,0,0,…,0 и вычислить при этом основные неизвестные, то получим X (2) . И так далее. Если свободным неизвестным переменным придадим значения 0,0,…,0,1 и вычислим основные неизвестные, то получим X (n-r) . Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде .
Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде , где - общее решение соответствующей однородной системы, а - частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0,0,…,0 и вычислив значения основных неизвестных.
Разберем на примерах.
Пример.
Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений 
.
Решение.
Ранг основной матрицы однородных систем линейных уравнений всегда равен рангу расширенной матрицы. Найдем ранг основной матрицы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем элемент a 1 1 = 9
основной матрицы системы. Найдем окаймляющий ненулевой минор второго порядка:
Минор второго порядка, отличный от нуля, найден. Переберем окаймляющие его миноры третьего порядка в поисках ненулевого:
Все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг основной и расширенной матрицы равен двум.
Базисным минором возьмем . Отметим для наглядности элементы системы, которые его образуют:
Третье уравнение исходной СЛАУ не участвует в образовании базисного минора, поэтому, может быть исключено:
Оставляем в правых частях уравнений слагаемые, содержащие основные неизвестные, а в правые части переносим слагаемые со свободными неизвестными:
Построим фундаментальную систему решений исходной однородной системы линейных уравнений. Фундаментальная система решений данной СЛАУ состоит из двух решений, так как исходная СЛАУ содержит четыре неизвестных переменных, а порядок ее базисного минора равен двум. Для нахождения X (1)
придадим свободным неизвестным переменным значения x 2 = 1, x 4 = 0
, тогда основные неизвестные найдем из системы уравнений
.
Теория общего равновесия Вальраса, являющаяся идеологической основой централизованной экономики, обладает рядом несомненных достоинств, а именно: целостностью и определенностью выводов, делающих ее весьма привлекательной для экономического анализа.
Однако в рамках этой теории невозможно адекватно описать децентрализованную экономику. Речь идет о механизме координации, о временном аспекте экономических процессов, о природе потоков и агентов.
Практика «нащупывания» равновесия в теории Вальраса, по существу, подразумевает, что никто из участников рынка не может влиять на цены, что каждый агент обладает совершенным знанием спроса и предложения, что процесс «нащупывания» происходит мгновенно, и, наконец, что осуществление сделок абсолютно недопустимо до тех пор, пока путем «нащупывания» не установлены «истинные цены», т. е. централизованный контроль над всеми потоками. Таким образом, эта модель, предполагающая весьма существенные ограничения, очень напоминает идеальный образ советской экономики .
Как утверждал польский экономист Ланге, «нет ничего важнее, чем понимание закономерностей децентрализованной экономики. Прежде всего, потому, что она – единственная реальность, с которой мы имеем дело».
Французский экономист Жан-Поль Фитусси (Jean Paul Fitoussi) утверждает, что между государством и рынком существует нечто промежуточное , и под этим промежуточным он понимает многообразие форм координации их отношений и связей. Эти двусторонние связи не сводятся ни к передаче приказа, ни к непосредственному контакту участников обмена в рамках определенного контракта. Приказ имеет значение только в той степени, в какой он исполняется. Это создает некоторую асимметрию между положениями начальника и подчиненного в пользу последнего. Именно во власти подчиненного находится исполнение приказа. Конечно, начальник может проверять исполнение приказов и, как это в свое время делал Сталин, наказать исполнителя. Но проверка – это тоже приказ, который воспроизводит изначальную асимметрию. За каждой проверкой следует проверка проверки. Таким образом, уже в самой основе централизованной экономики заложены истоки децентрализации – операциональной и информационной асимметрии – неоднородности.
По мнению Жака Сапира, можно выделить пять таких форм неоднородности.
1. Неоднородность продуктов, связанная с неодинаковыми возможностями их замещения. Это определяется не только природой продукта, но и конкретным способом его включения в тот или иной технологический или экономический процесс.
2. Неоднородность экономических агентов, которая не сводится только к различиям между наемным работником, предпринимателем и капиталистом. Господство означает ситуацию, в которой вокруг некоторых типов поведения или вокруг некоторых агентов происходит спонтанная организация других типов поведения или агентов, т. е. формирование коллектива. Переход от индивидуального к коллективному уровню осуществляется путем кооперации внутри коллектива организаций, которые выступают в роли экономических агентов. Они, в свою очередь, предполагают неоднородность методов взаимодействия и координации.
3. Неоднородность времени. Она может иметь две различные и взаимодополняющие формы. Одна из них связана с тем, что акты потребления, сбережения или производства у различных агентов имеют различную временную длительность – континиум. Это проблема неоднородности «времени действия». Возникновение другой формы неоднородности времени связано с тем, что мы называем временными рамками, в пределах которых решение каждого агента сохраняет свою силу. В этом случае можно говорить о «временных интервалах».
4. Неоднородность предприятий как локальных систем производства. Даже при условии идентичности выпускаемых продуктов поведение небольшого предприятия существенно отличается от поведения предприятия с большой численностью занятых. Кроме того, есть разница между производством простого и производством сложного продукта и т.д.
5. Неоднородность пространств, в которых разворачиваются экономические действия. Неодинаковая обеспеченность различных регионов факторами производства, как материальными, так и человеческими, естественно, воздействует на относительную цену этих факторов.
Типологизация неоднородностей Ж.Сапира была бы неполной без еще двух неоднородностей:
6. Неоднородность информационного пространства, обусловленная географическими и историко-культурными особенностями экономического пространства.
7. Политическая неоднородность регионов и стран, обеспечивающая защищенность инвестиций и доступность к информационным источникам, и существенно влияющая на их инвестиционную привлекательность. Пример экономического развития Китая весьма наглядно иллюстрирует это положение.
| Предыдущая |
Термин «система» употребляется в различных науках. Соответственно, разных ситуациях применяются различные определения системы: от философских до формальных. Для целей курса лучше всего подходит следующее определение: система – совокупность элементов, объединённых связями и функционирующих совместно для достижения цели.
Системы характеризуются рядом свойств, основные из которых делятся на три группы: статические, динамические и синтетические.
1.1 Статические свойства систем
Статическими свойствами называются особенности некоторого состояния системы. Это то чем обладает система в любой фиксированный момент времени.Целостность. Всякая система выступает как нечто единое, целое, обособленное, отличающееся от всего остального. Это свойство называется целостностью системы. Оно позволяет разделить весь мир на две части: систему и окружающую среду.
Открытость. Выделяемая, отличаемая от всего остального система не изолирована от окружающей среды. Наоборот, они связаны и обмениваются различными видами ресурсов (веществом, энергией, информацией и т.д.). Эта особенность обозначается термином «открытость».
Связи системы со средой носят направленный характер: по одним среда влияет на систему (входы системы), по другим система оказывает влияние на среду, что-то делает в среде, что-то выдаёт в среду (выходы системы). Описание входов и выходов системы называется моделью чёрного ящика. В такой модели отсутствует информация о внутренних особенностях системы. Несмотря на кажущуюся простоту, такой модели зачастую вполне достаточно для работы с системой.
Во многих случаях при управлении техникой или людьми информация только о входах и выходах системы позволяет успешно достигать цели. Однако для этого модель должна отвечать определённым требованиям. Например, пользователь может испытывать затруднения, если не будет знать, что в некоторых моделях телевизоров кнопку включения нужно не нажимать, а вытягивать. Поэтому для успешного управления модель должна содержать всю информацию, необходимую для достижения цели. При попытке удовлетворить это требование может возникнуть четыре типа ошибок, которые проистекают из того, что модель всегда содержит конечное число связей, тогда как у реальной системы количество связей неограниченно.
Ошибка первого рода возникает в том случае, когда субъект ошибочно рассматривает связь как существенную и принимает решение о её включении в модель. Это приводит к появлению в модели лишних, ненужных элементов. Ошибка второго рода, напротив, совершается тогда, когда принимается решение об исключении из модели якобы несущественной связи, без которой, на самом деле, достижение цели затруднено или вообще невозможно.
Ответ на вопрос о том, какая из ошибок хуже, зависит от контекста, в котором он задаётся. Понятно, что использование модели, содержащей ошибку, неизбежно ведёт к потерям. Потери могут быть небольшими, приемлемыми, нетерпимыми и недопустимыми. Урон, наносимый ошибкой первого рода связан с тем , что информация, внесённая ею, лишняя. При работе с такой моделью придётся тратить ресурсы на фиксацию и обработку лишней информации, например, тратить на неё память ЭВМ и время обработки. На качестве решения это, возможно, и не скажется, а на стоимости и своевременности скажется обязательно. Потери от ошибки второго рода – урон от того, что информации для полного достижения цели не хватит, цель не может быть достигнута в полной мере.
Теперь ясно, что хуже та ошибка, потери от которой больше, а это зависит от конкретных обстоятельств. Например, если время является критическим фактором, то ошибка первого рода становится гораздо более опасной, чем ошибка второго рода: вовремя принятое, пусть не наилучшее, решение предпочтительнее оптимального, но запоздавшего.
Ошибкой третьего рода принято считать последствия незнания. Для того, чтобы оценивать существенность некоторой связи, нужно знать, что она вообще есть. Если это не известно, то вопрос о включении связи в модель вообще не стоит. В том случае, если такая связь несущественна, то на практике её наличие в реальности и отсутствие в модели будет незаметно. Если же связь существенна, то возникнут трудности, аналогичные трудностям при ошибке второго рода. Разница состоит в том, что ошибку третьего рода сложнее исправить: для этого необходимо добывать новые знания.
Ошибка четвёртого рода возникает при ошибочном отнесении известной существенной связи к числу входов или выходов системы. Например, точно установлено, что в Англии 19-го века здоровье мужчин, носящих цилиндры, значительно превосходило здоровье мужчин, носящих кепки. Навряд ли из этого следует, что вид головного убора можно рассматривать как вход для системы прогнозирования состояния здоровья.
Внутренняя неоднородность систем, раличимость частей. Если заглянуть внутрь «чёрного ящика», то выяснится, что система неоднородна, не монолитна. Можно обнаружить , что различные качества в разных частях системы отличаются. Описание внутренней неоднородности системы сводится к обособлению относительно однородных участков, проведению границ между ними. Так появляется понятие о частях системы. При более детальном рассмотрении оказывается, что выделенные крупные части тоже неоднородны, что требует выделять ещё более мелкие части. В результате получается иерархическое описание частей системы, которое называется моделью состава.
Информация о составе системы может использоваться для работы с системой. Цели взаимодействия с системой могут быть различными, в связи с чем могут различаться и модели состава одной и той же системы. На первый взгляд различить части системы нетрудно, они «бросаются в глаза». В некоторых системах части возникают произвольно, в процессе естественного роста и развития (организмы, социумы и т.д.). Искусственные системы заведомо собираются из заранее известных частей (механизмы, здания и т.д.). Есть и смешанные типы систем, такие как заповедники, сельскохозяйственные системы. С другой стороны, с точки зрения ректора, студента, бухгалтера и хозяйственника университет состоит из разных частей. Самолёт состоит из разных частей с точки зрения пилота, стюардессы, пассажира. Трудности создания модели состава можно представить тремя положениями.
Во-первых, целое можно делить на часть по-разному. При этом способ деления определяется поставленной целью. Например, состав автомобиля по разному представляют начинающим автолюбителям, будущим профессиональным водителям, слесарям, готовящимся к работе в автосервисе, продавцам в автомагазинах. Естественно задать вопрос о том, существуют ли части системы «на самом деле»? Ответ содержится в формулировке рассматриваемого свойства: речь идёт о различимости, а не о разделимости частей. Можно различать нужные для достижения цели части системы, но нельзя разделять их.
Во-вторых, количество частей в модели состава зависит и от того, на каком уровне остановить дробление системы. Части на конечных ветвях получающегося иерархического дерева называются элементами. В различных обстоятельствах прекращение декомпозиции производится на разных уровнях. Например, при описании предстоящих работ приходится давать опытному работнику и новичку инструкции разной степени подробности. Таким образом, модель состава зависит от того, что считать элементарным. Встречаются случаи, когда элемент имеет природный, абсолютный характер (клетка, индивид, фонема, электрон).
В-третьих, любая система является частью большей системы, а иногда и нескольких систем сразу. Такую метасистему также можно делить на подсистемы по-разному. Это означает, что внешняя граница системы имеет относительный , условный характер. Определение границ системы производится с учётом целей субъекта, который будет использовать модель системы.
Структурированность. Свойство структурированности заключается в том, что части системы не изолированы, не независимы друг от друга; они связаны между собой, взаимодействуют друг с другом. При этом свойства системы существенно зависят от того, как именно взаимодействуют её части. Поэтому так частот важна информация о связях элементов системы. Перечень существенных связей между элементами системы называется моделью структуры системы. Наделённость любой системы определённой структурой и называется структурированностью.
Понятие структурированности дальше углубляет представление о целостности системы: связи как бы скрепляют части, удерживают их как целое. Целотность, отмеченная ранее как внешнее свойство, получает подкрепляющее объяснение изнутри системы – через структуру.
При построении модели структуры также встречаются определённые трудности. Первая из них связана с тем, что модель структуры определяется после того, как выбирается модель состава, и зависит от того, каков именно состав системы. Но даже при фиксированном составе модель структуры вариабельно. Связано это с возможностью по-разному определить существенность связей. Например, современному менеджеру рекомендуется наряду с формальной структурой его организации учитывать существование неформальных отношений между работниками, которые тоже влияют на функционирование организации. Вторая трудность проистекает из того, что каждый элемент системы, в свою очередь, представляет собой «маленький чёрный ящичек». Так что все четыре типа ошибок возможны при определении входов и выходов каждого элемента, включаемого в модель структуры.
1.2 ДИНАМИЧЕСКИЕ СВОЙСТВА СИСТЕМ
Если рассмотреть состояние системы в новый момент времени, то вновь можно обнаружить все четыре статических свойства. Но если наложить «фотографии» системы в разные моменты времени друг на друга, то обнаружится, что они отличаются в деталях: за время между двумя моментами наблюдения произошли какие-то изменения в системе и её окружении. Такие изменения могут быть важными при работе с системой, и, следовательно, должны быть отображены в описаниях системы и учтены при работе с нею. Особенности изменений со временем внутри системы и вне её и называются динамическими свойствами системы. Обычно различаются четыре динамических свойства системы.Функциональность. Процессы Y (t ), происходящие на выходах системы, рассматриваются как её функции. Функции системы – это её поведение во внешней среде, результаты её деятельности, продукция, производимая системой.
Из множественности выходов вытекает множественность функций, каждая из которых может быть кем-то и для чего-то использована. Поэтому одна и та же система может служить для разных целей. Субъект, использующий систему в своих целях , будет, естественно, оценивать её функции и упорядочивать их по отношению к своим потребностям. Так появляются понятия главной, второстепенной, нейтральной, нежелательной, лишней функции и т.д.
Стимулируемость. На входах системы также происходят определённые процессы X (t ), воздействующие на систему и превращающиеся после ряда преобразований в системе в Y (t ). Воздействия X (t ) называются стимулами, а сама подверженность любой системы воздействием извне и изменение её поведения под этими воздействиями – стимулируемостью.
Изменчивость системы со временем. В любой системе происходят изменения, которые необходимо учитывать. В терминах модели системы можно сказать, что изменяться могут значения внутренних переменных (параметров) Z (t ), состав и структура системы и любые их комбинации. Характер этих изменений тоже может быть различным. Поэтому могут рассматриваться дальнейшие классификации изменений.
Самая очевидная классификация – по скорости изменений (медленные, быстрые. Скорость изменений измеряется относительно какой-либо скорости, взятой за стандарт. Возможно введение большого количества градаций скоростей. Возможна также классификация тенденций перемен в системе, касающихся её структуры и состава.
Можно говорить о таких изменениях, которые не затрагивают структуры системы: одни элементы заменяются другим, эквивалентными; параметры Z (t ) могут меняться без изменения структуры. Такой тип динамики системы называют её функционированием. Изменения могут носить количественный характер: происходит наращивание состава системы, и хотя при этом автоматически меняется и её структура, это до некоторого момента не сказывается на свойствах системы (например, расширение мусорной свалки). Такие изменения называются ростом системы. При качественных изменениях системы происходит изменение её существенных свойств. Если такие изменения идут в позитивном направлении, они называются развитием. С теми же ресурсами развитая система добивается более высоких результатов, могут появиться новые позитивные качества (функции). Это связано с повышением уровня системности, организованности системы.
Рост происходит в основном за счёт потребления материальных ресурсов, развитие – за счёт усвоения и использования информации. Рост и развитие могут идти одновременно, но не обязательно они связаны между собой. Рост всегда ограничен (в силу ограниченности материальных ресурсов), а развитие извне не ограничено, поскольку информация о внешней среде неисчерпаема. Развитие есть результат обучения, однако обучение нельзя осуществить вместо обучаемого. Поэтому существует внутреннее ограничение на развитие. Если система «не желает» обучаться, она не сможет и не будет развиваться.
Кроме процессов роста и развития в системе могут происходить и обратные процессы. Обратные росту изменения называют спадом, сокращением, уменьшением. Обратное развитию изменение называют деградацией, утратой или ослаблением полезных свойств.
Рассмотренные изменения являются монотонными, то есть они направлены «в одну сторону». Очевидно, что монотонные изменения не могут длиться вечно. В истории любой системы можно выделить периоды спада и подъёма, стабильности и неустойчивости, последовательность которых образует индивидуальный жизненный цикл системы.
Можно использовать и другие классификации процессов , происходящих в системе: по предсказуемости процессы делятся на случайные и детерминированные; по типу зависимости от времени процессы делятся на монотонные, периодические, гармонические, импульсные и т.д.
Существование в изменяющейся среде. Изменяется не только данная система, но и все остальные. Для рассматриваемой системы это выглядит как непрерывное изменение окружающей среды. Это обстоятельство имеет множество последствий для самой системы, которая должна приспосабливаться к новым условиям для того, чтобы не погибнуть. При рассмотрении конкретной системы обычно уделяют внимание особенностям той или иной реакции системы, например, скорости реакции. Если рассматривать системы, хранящие информацию (книги, магнитные носители), то скорость реакции на изменения внешней среды должна быть минимальной для обеспечения сохранения информации. С другой стороны, скорость реакции системы управления должна во много раз превосходить скорость изменения окружающей среды, так как система должна выбрать управляющее воздействие ещё до того, как состояние окружающей среды необратимо изменится.
1.3 СИНТЕТИЧЕСКИЕ СВОЙСТВА СИСТЕМ
К синтетическим свойствам относятся обобщающие, интегральные, собирательные свойства, описывающие взаимодействия системы со средой и учитывающие целостность в самом общем понимании.Эмерджентность.
Объединение элементов в систему приводит к появлению качественно новых свойств, не выводящихся из свойств частей, присущих только самой системе и существующих только до тех пор, пока система составляет одно целое. Подобные качества системы называются
эмерджентными (от англ. «возникать»).
Примеры эмерджентных свойств можно найти в различных областях. Например, ни одна из частей самолёта летать не может, а самолёт, тем не менее, летает. Свойства воды, многие из которых до конца не изучены, не вытекают из свойств водорода и кислорода.
Пусть имеются два чёрных ящика, каждый из которых обладает одним входом, одним выходом и производит одну операцию - к числу на входе прибавляет единицу. При соединении таких элементов по схеме, приведённой на рисунке, получим систему без входов, но с двумя выходами. На каждом такте работы система будет выдавать большее число, при этом на одном входе будут появляться только чётные, а на другом – только нечётные числа.
 |
|
| а | б |
| Рис.1.1. Соединение элементов системы: а) система с двумя выходами; б) параллельное соединение элементов |
|
Эмерджентные свойства системы определяются её структурой. Это значит, что при различных соединениях элементов будут возникать различные эмерджентные свойства. Например, если соединить элементы параллельно, то функционально новая система не будет отличаться от одного элемента. Эмерджентность проявится в повышении надёжности системы за счёт параллельного соединения двух одинаковых элементов – то есть за счёт избыточности.
Следует отметить важный случай, когда элементы системы обладают всеми её свойствами. Такая ситуация характерна для фрактального построения системы. При этом принципы структурирования частей те же, что и у системы в целом. Примером фрактальной системы может служить организация, в которой управление построено тождественно на всех уровнях иерархии.
Неразделимость на части. Это свойство является, фактически, следствием эмерджентности. Оно подчёркивается особо из-за того, что его практическая важность велика, а недооценка встречается очень часто.
При изъятии из системы части происходит два важных события. Во-первых, при этом изменяется состав системы, а значит и её структура. Это будет уже другая система с отличающимися свойствами. Во-вторых, элемент, изъятый из системы, будет вести себя по другому в силу того, что изменится его окружение. Всё это говорит о том, при рассмотрении элемента отдельно от остальной системы следует соблюдать осторожность.
Ингерентность. Систем тем более ингерентна (от англ. inherent – «являющийся частью чего-либо»), чем лучше она согласована, приспособлена к окружающей среде, совместима с нею. Степень ингерентности бывает разной и может изменяться. Целесообразность рассмотрения ингерентности как одного из свойств системы связана с тем, что от неё зависят степень и качество осуществления системой избранной функции. В естественных системах ингерентность повышается путём естественного отбора. В искусственных системах ингерентность должна быть особой заботой конструктора.
В ряде случаев ингерентность обеспечивается с помощью промежуточных, посреднических систем. В качестве примеров можно привести адаптеры для использования зарубежных электроприборов совместно с розетками советского образца; промежуточное программное обеспечение (например, служба COM в Windows), позволяющая двум программам разных производителей обмениваться данными между собой.
Целесообразность. В создаваемых человеком системах подчинённость и структуры, и состава достижению поставленной цели настолько очевидна, что может быть признана фундаментальным свойством любой искусственной системы. Это свойство называется целесообразностью. Цель, ради которой создаётся система, определяет, какое эмерджентное свойство будет обеспечивать достижение цели, а это, в свою очередь, диктует выбор структуры и состава системы. Для того, чтобы распространить понятие целесообразности и на естественные системы, необходимо уточнить понятие цели. Уточнение проводится на примере искусственной системы.
История любой искусственной системы начинается в некоторый момент времени 0, когда существующее значение вектора состояния Y 0 оказывается неудовлетворительным, то есть возникает проблемная ситуация. Субъект недоволен этим состоянием и хотел бы его изменить. Пусть его удовлетворило бы значения вектора состояния Y*. Это есть первое определение цели. Далее обнаруживается, что Y* не существует сейчас и не может в силу ряда причин быть достигнутым в ближайшем будущем. Второй шаг в определении цели состоит в признании её желательным будущим состоянием. Тут же выясняется, что будущее не ограничено. Третий шаг в уточнении понятия цели состоит в оценке времени T*, когда желаемое состояние Y* может быть достигнуто в заданных условиях. Теперь цель становится двумерной, это точка (T*, Y*) на графике. Задача состоит в том, чтобы перейти из точки (0, Y 0) в точку (T*, Y*). Но оказывается, что пройти этот путь можно по разным траекториям , а реализована может быть только одна из них. Пусть выбор выпал на траекторию Y*(t
). Таким образом, под целью теперь понимается не только конечное состояние (T*, Y*), но и вся траектория Y*(t
) («промежуточные цели», «план»). Итак, цель есть желаемые будущие состояния Y*(t
).
По прошествии времени T* состояние Y* становится реальным. Поэтому появляется возможность определить цель как будущее реальное состояние. Это даёт возможность сказать, что свойством целесообразности обладают и естественные системы, что позволяет с единых позиций подходить к описанию систем любой природы. Основное же различие между естественными и искусственными системами состоит в том, что естественные системы, подчиняясь законам природы, реализуют объективные цели, а искусственные системы создаются для реализации субъективных целей.
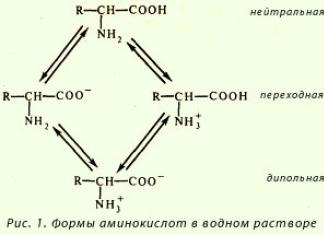
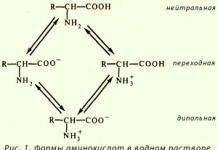
Наиболее общий признак любой неоднородной системы - наличие двух (или более) фаз, которые отделены друг от друга выраженной поверхностью раздела. Этим признаком неоднородные системы отличаются от растворов, которые также состоят из нескольких компонентов, образующих однородную смесь. Одну изфаз, сплошную, будем называть дисперсионной, а другую, мелкораздробленную ираспределенную в первой, - дисперсной фазой. В зависимости от вида дисперсионной среды различают неоднородные смеси, жидкие игазовые. В табл. 5.1приведена классификация неоднородных систем по виду дисперсной и дисперсионных фаз.
Таблица 5.1
Классификация неоднородных систем
Классификация и характеристика неоднородных систем
Неоднородной системой считается система, которая состоит из двух или нескольких фаз. Каждая фаза имеет свою поверхность раздела и ее можно механически отделить от другой.
Неоднородная система состоит из внутренней (дисперсной) фазы и внешней фазы (дисперсионной среды), в которой находятся частицы дисперсной фазы. Системы, в которых внешней фазой являются жидкости, называются неоднородными жидкими системами, а если газы - неоднородными газовыми системами. Неоднородные системы называют гетерогенными, а однородные - гомогенными. Под однородной жидкостной системой понимают чистую жидкость или раствор в ней каких-либо веществ. Неоднородной, или гетерогенной, жидкостной системой называют жидкость, в которой находятся какие-либо нерастворенные вещества в виде мельчайших частиц. Гетерогенные системы часто называют дисперсными.
Различают следующие виды неоднородных систем: суспензии, эмульсии, пены, пыли, дымы, туманы.
Суспензия - это система, состоящая из сплошной жидкой фазы, в которой взвешены твердые частицы. Например, соусы с мукой, крахмальное молоко, патока с кристаллами сахара.
Суспензии в зависимости от размеров частиц делятся на грубые (размер частиц более 100 мкм), тонкие (0,1-100 мкм) и коллоидные растворы, содержащие твердые частицы размером 0,1 мкм и меньше.
Эмульсия - это система, состоящая из жидкости и распределенных в ней капель другой жидкости, не растворившейся в первой. Это, например, молоко, смесь растительного масла и воды. Имеются газовые эмульсии, в которых дисперсионная среда - жидкость, а дисперсная фаза - газ.
Пена - это система, состоящая из жидкости и распределенных в ней пузырьков газа. Например, кремы и другие взбитые продукты. Пены по своим свойствам близки к эмульсиям.
Для эмульсий и пен характерна возможность перехода дисперсной фазы в дисперсионную среду и наоборот. Этот переход, возможный при определенном массовом соотношении фаз, называют инверсией фаз или просто инверсией.
Аэрозолями называют дисперсную систему с газообразной дисперсионной средой и твердой или жидкой дисперсной фазой, которая состоит из частиц от квазимолекулярного до микроскопического размера, обладающих свойством находиться во взвешенном состоянии более или менее продолжительное время. Это понятие объединяет пыли, дымы, туманы. Например, мучная пыль, образуемая при измельчении зерна, просеивании, транспортировке муки; сахарная пыль, образуемая при сушке сахара, и др. Дым образуется при сжигании твердого топлива, туман -при конденсации пара.
В аэрозолях дисперсионной средой является газ или воздух, а дисперсной фазой в пыли и дыме - твердые вещества, в туманах - жидкость.
Пыль и дым - системы, состоящие из газа и распределенных в них твердых частиц размерами 5-50 мкм и 0,3-5 мкм соответственно. Туман - это система, состоящая из газа и распределенных в нем капель жидкости размером 0,3-3 мкм, образовавшихся в результате конденсации.
Качественным показателем, характеризующим однородность частиц аэрозоля по размеру, является степень дисперсности. Аэрозоль называют монодисперсным, когда составляющие его частицы имеют одинаковый размер, и полидисперсным - при содержании в нем частиц разного размера. Монодисперсных аэрозолей в природе практически не существует. Имеются лишь некоторые аэрозоли, которые по размерам частиц лишь приближаются к монодисперсным системам (гифы грибов, специально получаемые туманы и др.).
Дисперсные или гетерогенные системы в зависимости от количества дисперсных фаз могут быть одно- и многокомпонентными. Например, многокомпонентной системой является молоко (имеет две дисперсные фазы: жир и белок); соусы (дисперсными фазами являются мука, жир и др.).
Методы разделения гетерогенных систем классифицируются в зависимости от размеров взвешенных частиц дисперсной фазы, разности плотностей дисперсной и сплошной фаз, а также вязкости сплошной фазы. Применяют следующие основные методы разделения: осаждение, фильтрование, центрифугирование, мокрое разделение, электроочистка.
Осаждение представляет собой процесс разделения, при котором взвешенные в жидкости или газе твердые или жидкие частицы дисперсной фазы отделяются от сплошной фазы под действием сил тяжести, центробежной или электростатической. Осаждение под действием силы тяжести называется отстаиванием.
Фильтрование - процесс разделения с помощью пористой перегородки, способной пропускать жидкость или газ и задерживать взвешенные в среде твердые частицы. Фильтрование осуществляется под действием сил давления и применяется для более тонкого, чем при осаждении, разделения суспензий и пылей.
Центрифугирование - процесс разделения суспензий и эмульсий под действием центробежной силы.
Мокрое разделение - процесс улавливания взвешенных в газе частиц с помощью какой-либо жидкости.
Электроочистка - очистка газов под воздействием электрических сил.
Методы разделения жидких и неоднородных газовых систем основаны на одинаковых принципах, но используемое оборудование имеет ряд особенностей.
§6. Неоднородная система линейных уравнений
Если в системе линейных уравнений (7.1) хотя бы один из свободных членов в i отличен от нуля, то такая система называется неоднородной.
Пусть задана неоднородная система линейных уравнений, которую в векторной форме можно представить в виде
, i = 1,2,.. .,к , (7.13)
Рассмотрим соответствующую однородную систему
i
=
1,2,...
,к
.
(7.14)
Пусть
вектор
является решением неоднородной системы
(7.13), а вектор
является решением однородной системы
(7.14). Тогда, легко видеть, что вектор
также является решением неоднородной
системы (7.13). Действительно
Теперь, используя формулу (7.12) общего решения однородного уравнения, имеем
где
любые числа изR
,
а
– фундаментальные решения однородной
системы.
Таким образом, решение неоднородной системы есть совокупность ее частного решения и общего решения соответствующей однородной системы.
Решение (7.15) называется общим решением неоднородной системы линейных уравнений. Из (7.15) следует, что совместная неоднородная система линейных уравнений имеет единственное решение, если ранг r (A ) основной матрицы А совпадает с числом n неизвестных системы (система Крамера), если же r (A ) n , то система имеет бесчисленное множество решений и эта совокупность решений эквивалентна подпространству решений соответствующей однородной системы уравнений размерности n – r .
Примеры.
1. Пусть дана неоднородная система уравнений, в которой число уравнений к = 3, а число неизвестных n = 4.
х 1 – х 2 + х 3 –2х 4 = 1,
х 1 – х 2 + 2х 3 – х 4 = 2,
5х 1 – 5х 2 + 8х 3 – 7х 4 = 3.
Определим ранги основной матрицы А и расширенной А * данной системы. Поскольку А и А * не нулевые матрицы и к = 3 n , поэтому 1 r (A ), r * (А * ) 3. Рассмотрим миноры второго порядка матриц А и А * :
Таким образом, среди миноров второго порядка матриц А и А * есть минор отличный от нуля, поэтому 2 r (A ), r * (A * ) 3. Теперь рассмотрим миноры третьего порядка
,
так как первый и второй столбец
пропорциональны. Аналогично и для минора
.
И так все миноры третьего порядка основной матрицы А равны нулю, следовательно, r (A ) = 2. Для расширенной матрицы А * еще имеются миноры третьего порядка
Следовательно, среди миноров третьего порядка расширенной матрицы А * есть минор отличный от нуля, поэтому r * (A * ) = 3. Это означает, что r (A ) r * (A * ) и тогда, на основании теоремы Корнекера – Капелли, делаем вывод, что данная система несовместна.
2. Решить систему уравнений
3х 1 + 2х 2 + х 3 + х 4 = 1,
3х 1 + 2х 2 – х 3 – 2х 4 = 2.
Для
данной системы
и поэтому 1
r
(A
),
r
*
(A
*
)
2. Рассмотрим для матриц A
и A
*
миноры второго порядка
Таким образом, r (A ) = r * (A * ) = 2, и, следовательно, система совместна. В качестве базовых выберем любые две переменные, для которых минор второго порядка, составленный из коэффициентов у этих переменных не равен нулю. Такими переменными могут быть, например,
х
3
и х
4 ,
так как
Тогда имеем
х 3 + х 4 = 1 – 3х 1 – 2х 2 ,
– х 3 – 2х 4 = 2 – 3х 1 – 2х 2 .
Определим
частное решение
неоднородной системы. Для этого положимх
1
= х
2
= 0.
х 3 + х 4 = 1,
– х 3 – 2х 4 = 2.
Решение
этой системы: х
3
= 4, х
4
= – 3, следовательно,
=
(0,0,4, –3).
Теперь определим общее решение соответствующего однородного уравнения
х 3 + х 4 = – 3х 1 – 2х 2 ,
–х 3 – 2х 4 = – 3х 1 – 2х 2 .
Положим: х 1 = 1, х 2 = 0
х 3 + х 4 = –3,
–х 3 – 2х 4 = –3.
Решение этой системы х 3 = –9, х 4 = 6.
Таким
образом
Теперь положим х 1 = 0, х 2 = 1
х 3 + х 4 = –2,
–х 3 – 2х 4 = –2.
Решение:
х
3
= – 6, х
4
= 4, и тогда
После
того как определены частное решение
,
неоднородного уравнения и фундаментальные
решения
и
соответствующего однородного уравнения,
записываем общее решение неоднородного
уравнения.
где
любые числа изR
.
