1°

1°. Уравнения на допирателната равнина и нормалата за случая на явно дефиниране на повърхнината.

Нека разгледаме едно от геометричните приложения на частни производни на функция на две променливи. Нека функцията z = е (x ;y)диференцируеми в точката (х 0; y 0)някаква област гÎ R 2. Нека изрежем повърхността S,представляващи функцията z,самолети x = x 0И y = y 0(фиг. 11).

Самолет X = х 0пресича повърхността Спо някаква линия z 0 (y),чието уравнение се получава чрез заместване в израза на първоначалната функция z ==е (x ;y)вместо Xчисла x 0 .Точка M 0 (x 0;y 0,е (x 0;y 0))принадлежи на кривата z 0 (y).Поради диференцируемата функция zв точката М 0функция z 0 (y)също е диференцируем в точката y =y 0 .Следователно в тази точка на равнината x = x 0към кривата z 0 (y)може да се начертае допирателна l 1.

Провеждане на подобни разсъждения за раздела при = y 0,нека изградим допирателна l 2към кривата z 0 (x)в точката X = x 0 -Директен 1 1 И 1 2 определят равнина, наречена допирателна равнинана повърхността Св точката М 0.

Нека създадем неговото уравнение. Тъй като равнината минава през точката Мо(x 0;y 0 ;z 0),тогава неговото уравнение може да бъде написано като

A(x - xo) + B(y - yo) + C (z - zo) = 0,

което може да се пренапише така:

z -z 0 = A 1 (x – x 0) + B 1 (y – y 0) (1)

(разделяйки уравнението на -C и обозначавайки ).

Ще намерим A 1и Б 1.

Допирателни уравнения 1 1 И 1 2 изглеждат като

съответно.

Допирателна l 1лежи в равнина a , следователно координатите на всички точки l 1отговарят на уравнение (1). Този факт може да се запише под формата на система

Разрешавайки тази система по отношение на B 1, получаваме това, извършвайки подобни разсъждения за допирателната l 3, лесно е да се установи, че .

Подмяна на стойностите A 1и B 1 в уравнение (1), получаваме желаното уравнение на допирателната равнина:

Права, минаваща през точка М 0и перпендикулярна на допирателната равнина, построена в тази точка на повърхността, се нарича нейна нормално.

Използвайки условието за перпендикулярност на права и равнина, лесно се получава канонични уравнениянормални:

Коментирайте.Формулите за допирателната равнина и нормалата към повърхността са получени за обикновени, т.е. неспециални точки от повърхността. Точка М 0повърхност се нарича специален,ако в този момент всички частни производни са равни на нула или поне една от тях не съществува. Ние не разглеждаме такива точки.

Пример. Напишете уравнения за допирателната равнина и нормалата към повърхността в нейната точка М(2; -1; 1).

Решение. Нека намерим частните производни на тази функция и техните стойности в точка M

От тук, прилагайки формули (2) и (3), ще имаме: z-1=2(x-2)+2(y+1)или 2х+2у-z-1=0- уравнение на допирателната равнина и - нормални уравнения.

2°. Уравнения на допирателната равнина и нормалата за случай на неявна дефиниция на повърхнината.

Ако повърхността Сдадено от уравнението F (x ; y;з)= 0, след това уравнения (2) и (3), като се вземе предвид факта, че частните производни могат да бъдат намерени като производни на неявна функция.

Определение 1 : Допирателната равнина към повърхността в дадена точка P (x 0, y 0, z 0) е равнина, минаваща през точка P и съдържаща всички допирателни, построени в точка P към всички възможни криви на тази повърхност, минаващи през точка P.

Нека повърхността s е дадена от уравнението Е (X, при, z) = 0 и точка П (х 0 , г 0 , z 0) принадлежи на тази повърхност. Нека изберем някаква крива на повърхността Л, минаваща през точката Р.

Нека X = X(t), при = при(t), z = z(t) - параметрични уравнениялинии Л.

Да приемем, че: 1) функция Е(X, при, z) е диференцируема в точката Ри не всички негови частни производни в тази точка са равни на нула; 2) функции X(t), при(t), z(t) също са диференцируеми.

Тъй като кривата принадлежи на повърхността s, координатите на всяка точка от тази крива, заместени в уравнението на повърхността, ще я превърнат в идентичност. Следователно е вярно идентичното равенство: Е [х(t), при(t), z (t)]= 0.

Разграничаване на тази идентичност по отношение на променливата t, използвайки верижното правило, получаваме ново идентично равенство, валидно във всички точки на кривата, включително в точката П (х 0 , г 0 , z 0):

Нека точка P съответства на стойността на параметъра t 0, т.е х 0 = х (t 0), г 0 = г (t 0), z 0 = z (t 0). След това последното отношение, изчислено в точката Р, ще приеме формата

Тази формула е скаларно произведение на два вектора. Първият е постоянен вектор

независимо от избора на крива на повърхността.

Вторият вектор е допирателен в точката Ркъм линията Л, което означава, че зависи от избора на линия на повърхността, тоест това е променлив вектор.

С въведените означения равенството е:

нека пренапишем как.

Значението му е следното: скаларното произведение е равно на нула, следователно векторите са перпендикулярни. Избиране на всички възможни криви, минаващи през точка Рвърху повърхност s, ще имаме различни допирателни вектори, конструирани в точката Ркъм тези редове; векторът не зависи от този избор и ще бъде перпендикулярен на всеки от тях, т.е. всички допирателни вектори са разположени в една и съща равнина, която по дефиниция е допирателна към повърхността s и точката Рв този случай тя се нарича допирателна точка. Векторът е векторът на посоката, нормален към повърхността.

Определение 2: Нормалата към повърхността s в точка P е права линия, минаваща през точка P и перпендикулярна на допирателната равнина, построена в тази точка.

Доказахме съществуването на допирателна равнина и, следователно, нормала към повърхността. Нека запишем техните уравнения:

Уравнение на допирателната равнина, построена в точка P (x0, y0, z0) към повърхността s, дадено от уравнението F(x, y, z) = 0;

Уравнение на нормалата, построена в точка Ркъм повърхността s.

Пример:Намерете уравнението на повърхността, образувана от въртенето на параболата:

z 2 = 2p (г +2)

около оста y, изчислете при условие, че точката M(3, 1, - 3)принадлежи на повърхността. Намерете уравненията на нормалната и допирателната равнина към повърхността в точка M.

Решение.Използвайки правилото за записване на ротационна повърхност, получаваме:

z 2 + х 2 = 2p (г +2) .

Замествайки координатите на точка M в това уравнение, изчисляваме стойността на параметъра p: 9 + 9 = 2р(1 + 2) . Записваме окончателния изглед на повърхността на въртене, преминаваща през точката М:

z 2 + х 2 = 6(y +2).

Сега ще намерим уравненията на нормалната и допирателната равнина, като използваме формулите, за които първо изчисляваме частните производни на функцията:

F(x, y) = z 2 + х 2- 6 (г +2):

Тогава уравнението на допирателната равнина приема формата 6(x - 3) - 6(y - 1) - 6(z + 3) = 0 или x - y - z - 5 = 0;

Нека разгледаме геометричните приложения на производната на функция на няколко променливи. Нека функция от две променливи е зададена имплицитно: . Тази функция в своята област на дефиниране е представена от определена повърхност (раздел 5.1). Нека вземем произволна точка на тази повърхност , в която и трите частни производни , , съществуват и са непрекъснати, като поне една от тях не е равна на нула.

Точка с такива характеристики се нарича обикновени повърхностна точка. Ако поне едно от горните изисквания не е изпълнено, точката се извиква специален повърхностна точка.

През точка, избрана на повърхността, могат да бъдат начертани много криви, всяка от които може да има допирателна.

Определение 5.8.1 . Равнината, в която са разположени всички допирателни към правите на повърхността, преминаващи през определена точка, се нарича допирателна равнина към тази повърхност в точката .

Да харчат дадена равнинадостатъчно е да има две допирателни, тоест две криви на повърхността. Това могат да бъдат криви, получени в резултат на разрязване на дадена повърхност с равнини, (фиг. 5.8.1).

Нека напишем уравнението на допирателна към крива, лежаща в пресечната точка на повърхността и равнината. Тъй като тази крива лежи в координатната система, уравнението на допирателната към нея в точката, в съответствие с параграф 2.7, има формата:

. (5.8.1)

Съответно уравнението на допирателната към кривата, лежаща в пресечната точка на повърхността и равнината в координатната система в една и съща точка, има формата:

. (5.8.2)

Нека използваме израза за производната на имплицитно определена функция (раздел 5.7). Тогава, а. Замествайки тези производни в (5.8.1) и (5.8.2), получаваме съответно:

; (5.8.3)

. (5.8.4)

Тъй като получените изрази не са нищо повече от уравнения на прави линии в канонична форма(т. 15), тогава от (5.8.3) получаваме вектора на посоката , и от (5.8.4) – . Векторни произведения на изкуствотоще даде нормален вектор към дадените допирателни линии и, следователно, към допирателната равнина:

От това следва, че уравнението на допирателната равнина към повърхността в точката има формата (точка 14):

Определение 5.8.2 . Права линия, прекарана през точка повърхност, перпендикулярна на допирателната равнина в тази точка, се нарича нормала към повърхността.

Тъй като насочващият вектор на нормалата към повърхността съвпада с нормалата към допирателната равнина, нормалното уравнение има формата:

.

Скаларно поле

Нека в пространството е определен регион, заемащ част или цялото пространство. Нека всяка точка от тази област според някакъв закон е свързана с определена скаларна величина (число).

Определение 5.9.1 . Област в пространството, всяка точка от която е свързана, съгласно добре известен закон, с определена скаларна величина, се нарича скаларно поле.

Ако някаква координатна система е свързана с района, например правоъгълна декартова система, тогава всяка точка придобива свои собствени координати. В този случай скаларната величина става функция на координатите: в равнината – , в тримерното пространство – . Самата функция, която описва това поле, често се нарича скаларно поле. В зависимост от размерността на пространството скаларното поле може да бъде плоско, триизмерно и др.

Трябва да се подчертае, че големината на скаларното поле зависи само от позицията на точката в региона, но не зависи от избора на координатна система.

Определение 5.9.2 . Скаларно поле, което зависи само от позицията на точка в региона, но не зависи от времето, се нарича стационарно.

Нестационарните скаларни полета, тоест зависещи от времето, няма да бъдат разглеждани в този раздел.

Примери за скаларни полета включват температурното поле, полето на налягането в атмосферата и полето на височината над нивото на океана.

Геометрично, скаларните полета често се представят с помощта на така наречените линии или нивелирани повърхности.

Определение 5.9.3 . Множеството от всички точки в пространството, в които скаларното поле има същото значение и се нарича равна повърхност или еквипотенциална повърхност. В плоския случай за скаларно поле това множество се нарича линия на ниво или еквипотенциална линия.

Очевидно уравнението на повърхността на нивото има формата , линии на ниво – . Като дадем константата в тези уравнения различни значения, получаваме семейство от повърхности или линии на ниво. например, (сфери, вложени една в друга с различни радиуси) или (семейство от елипси).

Примери за линии на ниво от физиката включват изотерми (линии на еднакви температури), изобари (линии на еднакво налягане); от геодезия - линии с еднаква височина и др.

А именно за това, което виждате в заглавието. По същество това е „пространствен аналог“ проблеми с намирането на допирателнаИ нормалникъм графиката на функция на една променлива и следователно не трябва да възникват трудности.

Нека започнем с основните въпроси: КАКВО Е допирателна равнина и КАКВО Е нормал? Много хора разбират тези понятия на ниво интуиция. Най-простият модел, който идва на ум, е топка, върху която лежи тънко плоско парче картон. Картонът е разположен възможно най-близо до сферата и я докосва в една точка. Освен това в точката на контакт се закрепва с игла, стърчаща право нагоре.

На теория има доста гениално определение на допирателната равнина. Представете си безплатно повърхности точката, която му принадлежи. Очевидно много минава през точката пространствени линии, които принадлежат на тази повърхност. Кой какви асоциации има? =) ...лично аз си представях октопод. Да приемем, че всяка такава линия има пространствена допирателнав точка .

Определение 1: допирателна равнинана повърхността в точка - това е самолет, съдържаща допирателни към всички криви, които принадлежат на дадена повърхност и минават през точката.

Определение 2: нормалнона повърхността в точка - това е прав, преминавайки през тази точкаперпендикулярна на допирателната равнина.

Просто и елегантно. Между другото, за да не умрете от скука от простотата на материала, малко по-късно ще споделя с вас една елегантна тайна, която ви позволява да забравите за тъпченето с различни определения ВЕДНЪЖ ЗАВИНАГИ.

Нека се запознаем с работещите формули и алгоритъма за решение, използвайки конкретен пример. В по-голямата част от проблемите е необходимо да се конструират както уравнението на допирателната равнина, така и нормалното уравнение:

Пример 1

Решение: ако повърхността е дадена от уравнението (т.е. имплицитно), тогава уравнението на допирателната равнина към дадена повърхност в точка може да се намери с помощта на следната формула:

Обръщам специално внимание на необичайни частични производни - техните не трябва да се бъркас частични производни на неявно определена функция (въпреки че повърхността е посочена имплицитно). При намирането на тези производни трябва да се ръководи от правила за диференциране на функция на три променливи, тоест при диференциране по отношение на която и да е променлива, другите две букви се считат за константи:

Без да излизаме от касата, намираме частичната производна в точката:

По същия начин:

Това беше най-неприятният момент от решението, в който грешка, ако не се допуска, то постоянно се появява. Има обаче ефективна техникапроверете за какво говорих в клас Производна по посока и градиент.

Всички „съставки“ са намерени и сега е въпрос на внимателно заместване с допълнителни опростявания:

– общо уравнениежеланата допирателна равнина.

Силно препоръчвам да проверите и този етап от решението. Първо трябва да се уверите, че координатите на допирателната точка наистина отговарят на намереното уравнение:

- истинско равенство.

Сега "премахваме" коефициентите общо уравнениеравнини и ги проверете за съвпадение или пропорционалност със съответните стойности. В този случай те са пропорционални. Както си спомняте от курс по аналитична геометрия, - Това нормален вектордопирателна равнина, и той също е водещ векторнормална права линия. Да композираме канонични уравнениянормали по вектор на точка и посока:

По принцип знаменателите могат да се намалят с две, но няма особена нужда от това

отговор:

Не е забранено уравненията да се обозначават с някакви букви, но пак защо? Тук вече е пределно ясно какво е какво.

Следващите два примера са за независимо решение. Малко „математически език“:

Пример 2

Намерете уравненията на допирателната равнина и нормалата към повърхността в точката.

И една интересна от техническа гледна точка задача:

Пример 3

Напишете уравнения за допирателната равнина и нормалата към повърхността в точка

В точката.

Има всички шансове не само да се объркате, но и да срещнете трудности при записа канонични уравнения на правата. И нормалните уравнения, както вероятно разбирате, обикновено се записват в тази форма. Въпреки че поради забрава или непознаване на някои нюанси, параметричната форма е повече от приемлива.

Приблизителни примери за окончателното изпълнение на решенията в края на урока.

Има ли допирателна равнина в някоя точка на повърхността? Като цяло, разбира се, че не. Класическият пример е конична повърхност и точка - допирателните в тази точка директно образуват конична повърхност и, разбира се, не лежат в една и съща равнина. Лесно е да се провери, че нещо не е наред аналитично: .

Друг източник на проблеми е фактът несъществуваневсяка частична производна в точка. Това обаче не означава, че в дадена точка няма единична допирателна равнина.

Но това беше по-скоро популярна наука, отколкото практически значима информация, и се връщаме към неотложни въпроси:

Как да напиша уравнения за допирателната равнина и нормалата в точка,
ако повърхността е зададена от изрична функция?

Нека го пренапишем имплицитно:

И използвайки същите принципи намираме частични производни:

Така формулата за допирателната равнина се трансформира в следното уравнение:

И съответно каноничните нормални уравнения:

както може би се досещате, - те вече са "истински" частни производни на функция на две променливив точката, която обозначавахме с буквата “z” и бяха открити 100500 пъти.

Моля, имайте предвид, че в тази статия е достатъчно да запомните първата формула, от която, ако е необходимо, е лесно да извлечете всичко останало (разбира се, с основно ниво на обучение). Това е точно подходът, който трябва да се използва при изучаването на точните науки, т.е. от минимум информация трябва да се стремим да „извлечем“ максимум изводи и последствия. „Разглеждането“ и съществуващите знания ще помогнат! Този принцип е полезен и защото най-вероятно ще ви спаси в критична ситуация, когато знаете много малко.

Нека разработим „модифицираните“ формули с няколко примера:

Пример 4

Напишете уравнения за допирателната равнина и нормалата към повърхността в точка .

Тук има леко наслагване с обозначенията - сега буквата обозначава точка от равнината, но какво да се прави - такава популярна буква...

Решение: нека съставим уравнението на желаната допирателна равнина по формулата:

Нека изчислим стойността на функцията в точката:

Нека изчислим Частични производни от 1-ви редв този момент:

Така:

внимателно, не бързайте:

Нека запишем каноничните уравнения на нормалата в точката:

отговор:

И последен пример за вашето собствено решение:

Пример 5

Запишете уравнения за допирателната равнина и нормалата към повърхността в точката.

Окончателно - защото съм обяснил практически всички технически моменти и няма какво специално да добавя. Дори самите функции, предложени в тази задача, са скучни и монотонни - на практика почти гарантирано ще попаднете на "полином" и в този смисъл пример № 2 с експонента изглежда като "черна овца". Между другото, много по-вероятно е да срещнете повърхност дадено от уравнениетои това е още една причина функцията да бъде включена в статията като номер две.

И накрая, обещаната тайна: как да избегнем тъпченето с дефиниции? (Разбира се, нямам предвид ситуацията, когато студентът трескаво тъпче нещо преди изпит)

Дефиницията на всяко понятие/явление/обект, на първо място, дава отговор на следния въпрос: КАКВО Е ТОВА? (кои/такива/такива/са). СъзнателноКогато отговаряте на този въпрос, трябва да се опитате да помислите значителнознаци, определеноидентифициране на конкретно понятие/явление/обект. Да, отначало се оказва някак езиковито, неточно и излишно (учителят ще ви коригира =)), но с времето се развива доста прилична научна реч.

Практикувайте върху най-абстрактните обекти, например отговорете на въпроса: кой е Чебурашка? Не е толкова просто ;-) Това е " приказен геройс големи уши, очи и кафява козина"? Далеч и много далеч от определението - никога не знаеш, че има герои с такива характеристики... Но това е много по-близо до определението: „Чебурашка е герой, измислен от писателя Едуард Успенски през 1966 г., който ... (списък на основните отличителни черти)» . Забележете колко добре започна

Изтеглете от Depositfiles

4. ТЕОРИЯ НА ПОВЪРХНОСТИТЕ.

4.1 ПОВЪРХНОСТНИ УРАВНЕНИЯ.

Повърхност в триизмерно пространствоможе да се даде:

1) имплицитно: Е ( х , г , z ) =0 (4.1)

2) изрично: z = f ( х , г ) (4.2)

3) параметрично: (4.3)

или:
(4.3’)

къде са скаларните аргументи
понякога наричани криволинейни координати. Например сферата
удобен за поставяне сферични координати:
.

4.2 ДОПИРАТЕЛНА РАВНИНА И НОРМАЛА КЪМ ПОВЪРХНОСТТА.

Ако правата лежи на повърхността (4.1), тогава координатите на нейните точки удовлетворяват уравнението на повърхността:

Разграничавайки тази идентичност, получаваме:

(4.4)

или
(4.4 ’ )

във всяка точка от кривата на повърхността. По този начин векторът на градиента в неособени точки на повърхността (в която функция (4.5) е диференцируема и
) е перпендикулярен на допирателните вектори към всякакви линии на повърхността, т.е. може да се използва като нормален вектор за съставяне на уравнението на допирателната равнина в точка M 0 (х 0 , г 0 , z 0 ) повърхност

(4.6)

и като вектор на посоката в нормалното уравнение:

(4.7)

В случай на изрично (4.2) спецификация на повърхността, уравненията съответно на допирателната равнина и нормалата приемат формата:

(4.8)

И
(4.9)

С параметричното представяне на повърхността (4.3), векторите
лежат в допирателната равнина и уравнението на допирателната равнина може да бъде написано като:

(4.10)

и тяхното векторно произведение може да се приеме като нормален вектор на посоката:

и нормалното уравнение може да се запише като:

(4.11)

Къде
— стойности на параметрите, съответстващи на точка М 0 .

По-нататък ще се ограничим до разглеждането само на такива повърхностни точки, където векторите

не е равно на нула и не е успоредно.

Пример 4.1 Създайте уравнения за допирателната равнина и нормалата в точка M 0 (1,1,2) към повърхността на параболоид на въртене
.

Решение: Тъй като параболоидното уравнение е дадено изрично, тогава съгласно (4.8) и (4.9) трябва да намерим
в точка М 0 :

, а в точка M 0
. Тогава уравнението на допирателната равнина в точка M 0 ще изглежда така:

2(х -1)+2(г -1)-(z-2)=0 или 2 х +2 г – з - 2=0 и нормалното уравнение
.

Пример 4.2 Съставете уравнения за допирателната равнина и нормалата в произволна точка на хеликоида
, .

Решение. тук,

Уравнение на допирателната равнина:

или

Нормални уравнения:

.

4.3 ПЪРВА КВАДРАТИЧНА ФОРМА НА ПОВЪРХНОСТТА.

Ако повърхността е дадена от уравнението

след това кривата
може да се даде от уравнението
(4.12)

Радиус-вектор диференциал
по кривата, съответстваща на преместването от точка М 0 до най-близката точка M, е равно на

(4.13)

защото
е диференциалът на дъгата на кривата, съответстваща на същото изместване), тогава

(4.14)

Къде .

Изразът от дясната страна на (4.14) се нарича първа квадратна форма на повърхността и играе огромна роля в теорията на повърхностите.

Интегрирам диференциалаdsвариращи от t 0 (съответства на точка М 0 ) до t (съответства на точка M), получаваме дължината на съответния сегмент от кривата

(4.15)

Познавайки първата квадратна форма на повърхността, можете да намерите не само дължините, но и ъглите между кривите.

Ако ду , дв са диференциали на криволинейни координати, съответстващи на безкрайно малко преместване по една крива, и
- от друга страна, след това като се вземе предвид (4.13):

(4.16)

Използване на формула

(4.17)

първата квадратна форма дава възможност да се изчисли площта на региона
повърхности.

Пример 4.3 На хеликоид намерете дължината на спиралата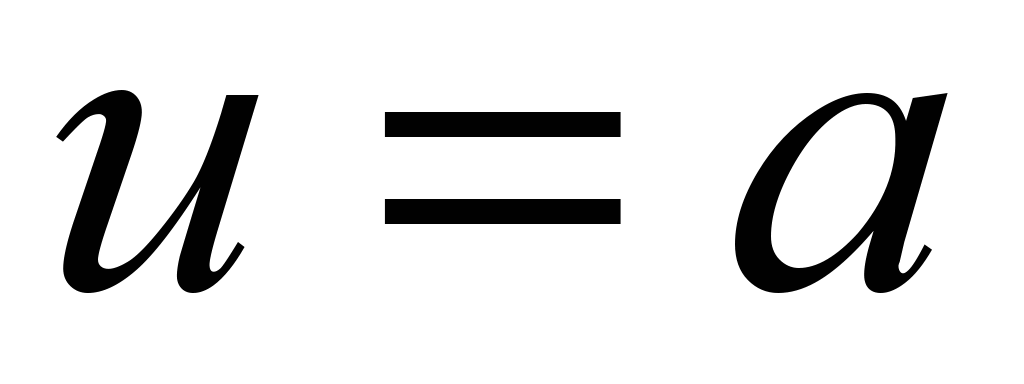
между две точки.

Решение. Тъй като на спиралата
, това . Да намерим в точката
първа квадратна форма. След като определи иv = t , получаваме уравнението на тази спираловидна линия във формата . Квадратна форма:

= - първа квадратна форма.

Тук. Във формула (4.15) в този случай
и дължина на дъгата:

=

4.4 ВТОРА КВАДРАТИЧНА ФОРМА НА ПОВЪРХНОСТТА.

Нека обозначим
- единичен вектор нормален към повърхността
:

(4.18) . (4.23)

Линия върху повърхност се нарича линия на кривина, ако нейната посока във всяка точка е основната посока.

4.6 КОНЦЕПЦИЯ ЗА ГЕОДЕЗИЧЕСКИ ЛИНИИ ВЪРХУ ПОВЪРХНОСТ.

Определение 4.1 . Крива върху повърхност се нарича геодезична, ако нейната главна нормала във всяка точка, където кривината е различна от нула, тя съвпада с нормалното на повърхността.

През всяка точка от повърхността във всяка посока минава само една геодезическа линия. На една сфера, например, големите кръгове са геодезически.

Параметризацията на повърхността се нарича полугеодезична, ако едно семейство координатни линии се състои от геодезични, а второто е ортогонално на него. Например, върху една сфера има меридиани (геодезични) и паралели.

Геодезическа линия на достатъчно малък сегмент е най-късата сред всички близки до нея криви, които свързват едни и същи точки.