যদিও জটিল সংখ্যার যোগ এবং বিয়োগ বীজগণিত আকারে করা আরও সুবিধাজনক, জটিল সংখ্যার ত্রিকোণমিতিক ফর্ম ব্যবহার করে গুণ এবং ভাগ করা সহজ।
ত্রিকোণমিতিক আকারে দেওয়া দুটি নির্বিচারে জটিল সংখ্যা নেওয়া যাক:
এই সংখ্যাগুলিকে গুণ করলে আমরা পাই:

কিন্তু ত্রিকোণমিতির সূত্র অনুযায়ী

![]()
এইভাবে, জটিল সংখ্যাগুলিকে গুণ করার সময়, তাদের মডুলি গুণিত হয়, এবং আর্গুমেন্টগুলি

ভাঁজ আপ যেহেতু এই ক্ষেত্রে মডিউলগুলি আলাদাভাবে রূপান্তরিত হয়, এবং আর্গুমেন্টগুলি - আলাদাভাবে, ত্রিকোণমিতিক আকারে গুণন সম্পাদন করা বীজগণিত আকারের চেয়ে সহজ।
সমতা থেকে (1) নিম্নলিখিত সম্পর্কগুলি অনুসরণ করে:

যেহেতু ভাগ হচ্ছে গুণের বিপরীত ক্রিয়া, তাই আমরা তা পাই

অন্য কথায়, ভাগফলের মডুলাস লভ্যাংশ এবং ভাজকের মডিউলির অনুপাতের সমান এবং ভাগফলের যুক্তি হল লভ্যাংশ এবং ভাজকের আর্গুমেন্টের মধ্যে পার্থক্য।
আমাদের এখন বসবাস করা যাক জ্যামিতিক ইন্দ্রিয়জটিল সংখ্যা গুণ করা। সূত্র (1) - (3) দেখায় যে পণ্যটি খুঁজে পেতে, আপনাকে প্রথমে তার যুক্তি পরিবর্তন না করেই সংখ্যার মডুলাস বাড়াতে হবে, এবং তারপর তার মডুলাস পরিবর্তন না করে ফলাফলের সংখ্যার যুক্তি বাড়াতে হবে। এই ক্রিয়াকলাপের প্রথমটি জ্যামিতিকভাবে বোঝায় একটি সহগ সহ O বিন্দুর সাপেক্ষে সমতুল্যতা, এবং দ্বিতীয়টির অর্থ হল O বিন্দুর সাপেক্ষে একটি ঘূর্ণন সমান একটি কোণ দ্বারা এখানে একটি ফ্যাক্টর ধ্রুবক এবং অন্যটি পরিবর্তনশীল, আমরা ফলাফলটি প্রণয়ন করতে পারি নিম্নরূপ: সূত্র
যদিও জটিল সংখ্যার যোগ এবং বিয়োগ বীজগণিত আকারে করা আরও সুবিধাজনক, জটিল সংখ্যার ত্রিকোণমিতিক ফর্ম ব্যবহার করে গুণ এবং ভাগ করা সহজ।
ত্রিকোণমিতিক আকারে দেওয়া দুটি নির্বিচারে জটিল সংখ্যা নেওয়া যাক:
এই সংখ্যাগুলিকে গুণ করলে আমরা পাই:

কিন্তু ত্রিকোণমিতির সূত্র অনুযায়ী

![]()
এইভাবে, জটিল সংখ্যাগুলিকে গুণ করার সময়, তাদের মডুলি গুণিত হয়, এবং আর্গুমেন্টগুলি

ভাঁজ আপ যেহেতু এই ক্ষেত্রে মডিউলগুলি আলাদাভাবে রূপান্তরিত হয়, এবং আর্গুমেন্টগুলি - আলাদাভাবে, ত্রিকোণমিতিক আকারে গুণন সম্পাদন করা বীজগণিত আকারের চেয়ে সহজ।
সমতা থেকে (1) নিম্নলিখিত সম্পর্কগুলি অনুসরণ করে:

যেহেতু ভাগ হচ্ছে গুণের বিপরীত ক্রিয়া, তাই আমরা তা পাই

অন্য কথায়, ভাগফলের মডুলাস লভ্যাংশ এবং ভাজকের মডিউলির অনুপাতের সমান এবং ভাগফলের যুক্তি হল লভ্যাংশ এবং ভাজকের আর্গুমেন্টের মধ্যে পার্থক্য।
আসুন এখন জটিল সংখ্যার গুণের জ্যামিতিক অর্থ নিয়ে আলোচনা করা যাক। সূত্র (1) - (3) দেখায় যে পণ্যটি খুঁজে পেতে, আপনাকে প্রথমে তার যুক্তি পরিবর্তন না করেই সংখ্যার মডুলাস বাড়াতে হবে, এবং তারপর তার মডুলাস পরিবর্তন না করে ফলাফলের সংখ্যার যুক্তি বাড়াতে হবে। এই ক্রিয়াকলাপের প্রথমটি জ্যামিতিকভাবে বোঝায় একটি সহগ সহ O বিন্দুর সাপেক্ষে সমতুল্যতা, এবং দ্বিতীয়টির অর্থ হল O বিন্দুর সাপেক্ষে একটি ঘূর্ণন সমান একটি কোণ দ্বারা এখানে একটি ফ্যাক্টর ধ্রুবক এবং অন্যটি পরিবর্তনশীল, আমরা ফলাফলটি প্রণয়ন করতে পারি নিম্নরূপ: সূত্র
জটিল সংখ্যা- এটি আমাদের পরিচিত অনেকের একটি ন্যূনতম বিস্তার বাস্তব সংখ্যা. তাদের মৌলিক পার্থক্য হল যে একটি উপাদান উপস্থিত হয় যা বর্গ করার সময় -1 দেয়, যেমন আমি, বা।
যেকোনো জটিল সংখ্যা দুটি অংশ নিয়ে গঠিত: বাস্তব এবং কাল্পনিক:
সুতরাং, এটা স্পষ্ট যে বাস্তব সংখ্যার সেটটি একটি শূন্য কাল্পনিক অংশ সহ জটিল সংখ্যার সেটের সাথে মিলে যায়।
জটিল সংখ্যার সেটের জন্য সবচেয়ে জনপ্রিয় মডেল হল সাধারণ সমতল। প্রতিটি বিন্দুর প্রথম স্থানাঙ্ক হবে তার বাস্তব অংশ, এবং দ্বিতীয়টি হবে তার কাল্পনিক অংশ। তারপর জটিল সংখ্যার ভূমিকা হবে বিন্দুতে (0,0) শুরু সহ ভেক্টর।
জটিল সংখ্যার উপর অপারেশন।
প্রকৃতপক্ষে, আমরা যদি জটিল সংখ্যার সেটের মডেলটি বিবেচনা করি, তবে এটি স্বজ্ঞাতভাবে স্পষ্ট যে দুটি জটিল সংখ্যার যোগ (বিয়োগ) এবং গুণ ভেক্টরের অনুরূপ ক্রিয়াকলাপগুলির মতোই সঞ্চালিত হয়। এবং এই মানে ভেক্টর পণ্যভেক্টর, কারণ এই অপারেশনের ফলাফল আবার একটি ভেক্টর।
1.1 সংযোজন।
(যেমন আপনি দেখতে পাচ্ছেন, এই অপারেশনটি ঠিক এর সাথে মিলে যায়)
1.2 বিয়োগ, একইভাবে, নিম্নলিখিত নিয়ম অনুযায়ী উত্পাদিত হয়:
2. গুণ।
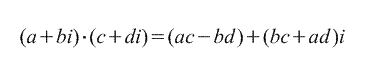
3. বিভাগ।
গুণনের বিপরীত অপারেশন হিসাবে সহজভাবে সংজ্ঞায়িত।

একটি জটিল সংখ্যা z এর মডুলাস হল নিম্নোক্ত পরিমাণ:
 ,
,
স্পষ্টতই, এটি আবার, ভেক্টর (a,b) এর মডুলাস (দৈর্ঘ্য)।
প্রায়শই, একটি জটিল সংখ্যার মডুলাস হিসাবে চিহ্নিত করা হয় ρ.
এটা যে সক্রিয় আউট
z = ρ(cosφ+isinφ).

জটিল সংখ্যা লেখার ত্রিকোণমিতিক ফর্ম থেকে নিম্নলিখিতগুলি সরাসরি অনুসরণ করে: সূত্র :

শেষ সূত্র বলা হয় Moivre এর সূত্র. সূত্রটি সরাসরি এটি থেকে উদ্ভূত হয় একটি জটিল সংখ্যার nম মূল:

এইভাবে, জটিল সংখ্যা z এর n তম মূল রয়েছে।
একটি জটিল সংখ্যা হল ফর্মের একটি সংখ্যা, যেখানে এবং বাস্তব সংখ্যা, তথাকথিত কাল্পনিক একক. নম্বরে কল করা হয় বাস্তব অংশ() জটিল সংখ্যা, সংখ্যা বলা হয় কাল্পনিক অংশ () জটিল সংখ্যা।
জটিল সংখ্যা দ্বারা প্রতিনিধিত্ব করা হয় জটিল সমতল:

উপরে উল্লিখিত হিসাবে, একটি অক্ষর সাধারণত বাস্তব সংখ্যার সেট বোঝায়। অনেকএকই জটিল সংখ্যাসাধারণত একটি "গাঢ়" বা ঘন অক্ষর দ্বারা চিহ্নিত করা হয়। অতএব, চিঠিটি অঙ্কনের উপর স্থাপন করা উচিত, এটি নির্দেশ করে যে আমাদের একটি জটিল সমতল রয়েছে।
একটি জটিল সংখ্যার বীজগণিতীয় রূপ। জটিল সংখ্যার যোগ, বিয়োগ, গুণ ও ভাগ
জটিল সংখ্যার সংযোজন
দুটি জটিল সংখ্যা যোগ করার জন্য, আপনাকে তাদের বাস্তব এবং কাল্পনিক অংশ যোগ করতে হবে:
z 1 + z 2 = (a 1 + a 2) + i*(b 1 + b 2)।
জটিল সংখ্যার জন্য, প্রথম শ্রেণীর নিয়মটি বৈধ: z 1 + z 2 = z 2 + z 1 – পদগুলিকে পুনর্বিন্যাস করলে যোগফল পরিবর্তিত হয় না।
জটিল সংখ্যা বিয়োগ করা
ক্রিয়াটি যোগের অনুরূপ, একমাত্র বিশেষত্ব হল সাবট্রাহেন্ডটি বন্ধনীতে স্থাপন করা প্রয়োজন, এবং তারপর বন্ধনীগুলিকে চিহ্নের পরিবর্তনের সাথে আদর্শ উপায়ে খোলা উচিত:
z 1 + z 2 = (a 1 – a 2) + i*(b 1 – b 2)
জটিল সংখ্যা গুণ করা
জটিল সংখ্যার মৌলিক সমতা:
জটিল সংখ্যার গুণফল:
z 1 * z 2 = (a 1 + i*b 1)*(a 2 + i*b 2) = a 1 *a 2 + a 1 *i*b 2 + a 2 *i*b 1 + i 2 *b 1 *b 2 = a 1 *a 2 - b 1 *b 2 +i*(a 1 *b 2 +a 2 *b 1)।
যোগফলের মতো, জটিল সংখ্যার গুণফল পরিবর্তনযোগ্য, অর্থাৎ, সমতা সত্য: .
জটিল সংখ্যার বিভাজন
সংখ্যার বিভাজন করা হয় হর এবং লবকে হর এর সংযোজিত রাশি দ্বারা গুণ করে.
2 প্রশ্ন। জটিল সমতল। জটিল সংখ্যার মডুলাস এবং আর্গুমেন্ট
প্রতিটি জটিল সংখ্যা z = a + i*b স্থানাঙ্ক (a;b) সহ একটি বিন্দুর সাথে যুক্ত হতে পারে এবং বিপরীতভাবে, স্থানাঙ্ক (c;d) সহ প্রতিটি বিন্দু একটি জটিল সংখ্যা w = c + i* এর সাথে যুক্ত হতে পারে d এইভাবে, সমতলের বিন্দু এবং জটিল সংখ্যার সেটের মধ্যে একটি এক থেকে এক চিঠিপত্র প্রতিষ্ঠিত হয়। অতএব, জটিল সংখ্যাগুলিকে সমতলে বিন্দু হিসাবে উপস্থাপন করা যেতে পারে। যে সমতলে জটিল সংখ্যাগুলি চিত্রিত করা হয় তাকে সাধারণত বলা হয় জটিল সমতল.

যাইহোক, প্রায়শই জটিল সংখ্যাগুলিকে O বিন্দুতে শুরু করে ভেক্টর হিসাবে চিত্রিত করা হয়, যথা, জটিল সংখ্যা z = a + i*b স্থানাঙ্ক (a;b) সহ একটি বিন্দুর ব্যাসার্ধ ভেক্টর হিসাবে চিত্রিত হয়। এই ক্ষেত্রে, পূর্ববর্তী উদাহরণ থেকে জটিল সংখ্যার চিত্রটি এরকম হবে: 
দুটি জটিল সংখ্যার যোগফলের চিত্রটি একটি ভেক্টর যা সংখ্যা এবং . অন্য কথায়, যখন জটিল সংখ্যা যোগ করা হয়, তখন তাদের প্রতিনিধিত্বকারী ভেক্টরগুলিও যোগ করা হয়।

জটিল সংখ্যা z = a + i*b একটি ব্যাসার্ধ ভেক্টর দ্বারা উপস্থাপন করা যাক। তারপর এই ভেক্টরের দৈর্ঘ্য বলা হয় মডিউলসংখ্যা z এবং |z| দ্বারা চিহ্নিত করা হয় .
|
|

অক্ষ সহ একটি সংখ্যার ব্যাসার্ধ ভেক্টর দ্বারা গঠিত কোণ বলা হয় যুক্তিসংখ্যা এবং arg z দ্বারা চিহ্নিত করা হয়। সংখ্যার যুক্তিটি স্বতন্ত্রভাবে নির্ধারিত হয় না, তবে একটি গুণিতকের মধ্যে। যাইহোক, সাধারণত আর্গুমেন্টটি 0 থেকে রেঞ্জে বা - থেকে থেকে রেঞ্জে নির্দিষ্ট করা হয়। উপরন্তু, সংখ্যা একটি অনির্ধারিত যুক্তি আছে.
এই সম্পর্ক ব্যবহার করে, আপনি একটি জটিল সংখ্যার যুক্তি খুঁজে পেতে পারেন:
তাছাড়া, প্রথম সূত্রটি বৈধ যদি সংখ্যাটির চিত্রটি প্রথম বা চতুর্থ ত্রৈমাসিক হয় এবং দ্বিতীয়টি যদি দ্বিতীয় বা তৃতীয় হয়। যদি , তাহলে জটিল সংখ্যাটি Oy অক্ষের একটি ভেক্টর দ্বারা উপস্থাপিত হয় এবং এর আর্গুমেন্ট /2 বা 3*/2 এর সমান।
আসুন আরেকটি দরকারী সূত্র পান। ধরুন z = a + i*b। তারপর,


























