Expanding polynomials to obtain a product can sometimes seem confusing. But it's not that difficult if you understand the process step by step. The article describes in detail how to factor a quadratic trinomial.

Many people do not understand how to factor a square trinomial, and why this is done. At first it may seem like a futile exercise. But in mathematics nothing is done for nothing. The transformation is necessary to simplify the expression and ease of calculation.

A polynomial of the form – ax²+bx+c, called a quadratic trinomial. The term "a" must be negative or positive. In practice, this expression is called a quadratic equation. Therefore, sometimes they say it differently: how to decompose quadratic equation.

Interesting! A polynomial is called a square because of its largest degree, the square. And a trinomial - because of the 3 components.

Some other types of polynomials:

• linear binomial (6x+8);
• cubic quadrinomial (x³+4x²-2x+9).

Factoring a quadratic trinomial

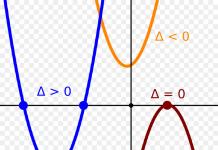
First, the expression is equal to zero, then you need to find the values ​​of the roots x1 and x2. There may be no roots, there may be one or two roots. The presence of roots is determined by the discriminant. You need to know its formula by heart: D=b²-4ac.

If the result D is negative, there are no roots. If positive, there are two roots. If the result is zero, the root is one. The roots are also calculated using the formula.

If, when calculating the discriminant, the result is zero, you can use any of the formulas. In practice, the formula is simply shortened: -b / 2a.

Formulas for different meanings discriminants differ.

If D is positive:

If D is zero:

Online calculators

On the Internet there is online calculator. It can be used to perform factorization. Some resources provide the opportunity to view the solution step by step. Such services help to better understand the topic, but you need to try to understand it well.

Useful video: Factoring a quadratic trinomial

Examples

We invite you to view simple examples, how to factor a quadratic equation.

Example 1

This clearly shows that the result is two x's because D is positive. They need to be substituted into the formula. If the roots turn out to be negative, the sign in the formula changes to the opposite.

We know the formula for factoring a quadratic trinomial: a(x-x1)(x-x2). We put the values ​​in brackets: (x+3)(x+2/3). There is no number before a term in a power. This means that there is one there, it goes down.

Example 2

This example clearly shows how to solve an equation that has one root.

We substitute the resulting value:

Example 3

Given: 5x²+3x+7

First, let's calculate the discriminant, as in previous cases.

D=9-4*5*7=9-140= -131.

The discriminant is negative, which means there are no roots.

After receiving the result, you should open the brackets and check the result. The original trinomial should appear.

Alternative solution

Some people were never able to make friends with the discriminator. There is another way to factorize a quadratic trinomial. For convenience, the method is shown with an example.

Given: x²+3x-10

We know that we should get 2 brackets: (_)(_). When the expression looks like this: x²+bx+c, at the beginning of each bracket we put x: (x_)(x_). The remaining two numbers are the product that gives “c”, i.e. in this case -10. The only way to find out what numbers these are is by selection. The substituted numbers must correspond to the remaining term.

For example, multiplying the following numbers gives -10:

• -1, 10;
• -10, 1;
• -5, 2;
• -2, 5.

1. (x-1)(x+10) = x2+10x-x-10 = x2+9x-10. No.
2. (x-10)(x+1) = x2+x-10x-10 = x2-9x-10. No.
3. (x-5)(x+2) = x2+2x-5x-10 = x2-3x-10. No.
4. (x-2)(x+5) = x2+5x-2x-10 = x2+3x-10. Fits.

This means that the transformation of the expression x2+3x-10 looks like this: (x-2)(x+5).

Important! You should be careful not to confuse the signs.

Expansion of a complex trinomial

If “a” is greater than one, difficulties begin. But everything is not as difficult as it seems.

To factorize, you first need to see if anything can be factored out.

For example, given the expression: 3x²+9x-30. Here the number 3 is taken out of brackets:

3(x²+3x-10). The result is the already well-known trinomial. The answer looks like this: 3(x-2)(x+5)

How to decompose if the term that is in the square is negative? In this case, the number -1 is taken out of brackets. For example: -x²-10x-8. The expression will then look like this:

The scheme differs little from the previous one. There are just a few new things. Let's say the expression is given: 2x²+7x+3. The answer is also written in 2 brackets that need to be filled in (_)(_). In the 2nd bracket is written x, and in the 1st what is left. It looks like this: (2x_)(x_). Otherwise, the previous scheme is repeated.

The number 3 is given by the numbers:

• -1, -3;
• -3, -1;
• 3, 1;
• 1, 3.

We solve equations by substituting these numbers. The last option is suitable. This means that the transformation of the expression 2x²+7x+3 looks like this: (2x+1)(x+3).

Other cases

It is not always possible to convert an expression. With the second method, solving the equation is not required. But the possibility of transforming terms into a product is checked only through the discriminant.

It is worth practicing solving quadratic equations so that when using the formulas there are no difficulties.

Useful video: factoring a trinomial

Conclusion

You can use it in any way. But it’s better to practice both until they become automatic. Also, learning how to solve quadratic equations well and factor polynomials is necessary for those who are planning to connect their lives with mathematics. All the following mathematical topics are built on this.

8 examples of factorization of polynomials are given. They include examples with solving quadratic and biquadratic equations, examples with recurrent polynomials and examples with finding integer roots of polynomials of the third and fourth degree.

Content

See also: Methods for factoring polynomials
Roots of a quadratic equation
Solving cubic equations

1. Examples with solving a quadratic equation

Example 1.1

x 4 + x 3 - 6 x 2.

We take out x 2 outside of brackets:
.
2 + x - 6 = 0:
.
Roots of the equation:
, .

.

Example 1.2

Factor the third degree polynomial:
x 3 + 6 x 2 + 9 x.

Let's take x out of brackets:
.
Solving the quadratic equation x 2 + 6 x + 9 = 0:
Its discriminant: .
Since the discriminant is zero, the roots of the equation are multiples: ;
.

From here we obtain the factorization of the polynomial:
.

Example 1.3

Factor the fifth degree polynomial:
x 5 - 2 x 4 + 10 x 3.

We take out x 3 outside of brackets:
.
Solving the quadratic equation x 2 - 2 x + 10 = 0.
Its discriminant: .
Since the discriminant is less than zero, the roots of the equation are complex: ;
, .

The factorization of the polynomial has the form:
.

If we are interested in factorization with real coefficients, then:
.

Examples of factoring polynomials using formulas

Examples with biquadratic polynomials

Example 2.1

Factor the biquadratic polynomial:
x 4 + x 2 - 20.

Let's apply the formulas:
a 2 + 2 ab + b 2 = (a + b) 2;
a 2 - b 2 = (a - b)(a + b).

;
.

Example 2.2

Factor the polynomial that reduces to a biquadratic one:
x 8 + x 4 + 1.

Let's apply the formulas:
a 2 + 2 ab + b 2 = (a + b) 2;
a 2 - b 2 = (a - b)(a + b):

;

;
.

Example 2.3 with recurrent polynomial

Factor the reciprocal polynomial:
.

A reciprocal polynomial has odd degree. Therefore it has root x = - 1 . Divide the polynomial by x - (-1) = x + 1. As a result we get:
.
Let's make a substitution:
, ;
;


;
.

Examples of factoring polynomials with integer roots

Example 3.1

Factor the polynomial:
.

Let's assume that the equation

6
-6, -3, -2, -1, 1, 2, 3, 6 .
(-6) 3 - 6·(-6) 2 + 11·(-6) - 6 = -504;
(-3) 3 - 6·(-3) 2 + 11·(-3) - 6 = -120;
(-2) 3 - 6·(-2) 2 + 11·(-2) - 6 = -60;
(-1) 3 - 6·(-1) 2 + 11·(-1) - 6 = -24;
1 3 - 6 1 2 + 11 1 - 6 = 0;
2 3 - 6 2 2 + 11 2 - 6 = 0;
3 3 - 6 3 2 + 11 3 - 6 = 0;
6 3 - 6 6 2 + 11 6 - 6 = 60.

So, we found three roots:
x 1 = 1 , x 2 = 2 , x 3 = 3 .
Since the original polynomial is of the third degree, it has no more than three roots. Since we found three roots, they are simple. Then
.

Example 3.2

Factor the polynomial:
.

Let's assume that the equation

has at least one whole root. Then it is a divisor of the number 2 (member without x). That is, the whole root can be one of the numbers:
-2, -1, 1, 2 .
We substitute these values ​​one by one:
(-2) 4 + 2·(-2) 3 + 3·(-2) 3 + 4·(-2) + 2 = 6 ;
(-1) 4 + 2·(-1) 3 + 3·(-1) 3 + 4·(-1) + 2 = 0 ;
1 4 + 2 1 3 + 3 1 3 + 4 1 + 2 = 12;
2 4 + 2 2 3 + 3 2 3 + 4 2 + 2 = 54.

So, we found one root:
x 1 = -1 .
Divide the polynomial by x - x 1 = x - (-1) = x + 1:


Then,
.

Now we need to solve the third degree equation:
.
If we assume that this equation has an integer root, then it is a divisor of the number 2 (member without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2 .
Let's substitute x = -1 :
.

So, we have found another root x 2 = -1 . It would be possible, as in the previous case, to divide the polynomial by , but we will group the terms:
.

In order to factorize, it is necessary to simplify the expressions. This is necessary so that it can be further reduced. The expansion of a polynomial makes sense when its degree is not lower than two. A polynomial with the first degree is called linear.

The article will cover all the concepts of decomposition, theoretical foundations and methods of factoring a polynomial.

Theory

Theorem 1

When any polynomial with degree n, having the form P n x = a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0, are represented as a product with a constant factor with the highest degree a n and n linear factors (x - x i), i = 1, 2, ..., n, then P n (x) = a n (x - x n) (x - x n - 1) · . . . · (x - x 1) , where x i, i = 1, 2, …, n are the roots of the polynomial.

The theorem is intended for roots of complex type x i, i = 1, 2, …, n and for complex coefficients a k, k = 0, 1, 2, …, n. This is the basis of any decomposition.

When coefficients of the form a k, k = 0, 1, 2, …, n are real numbers, Then complex roots, which will occur in conjugate pairs. For example, roots x 1 and x 2 related to a polynomial of the form P n x = a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 are considered complex conjugate, then the other roots are real, from which we obtain that the polynomial takes the form P n (x) = a n (x - x n) (x - x n - 1) · . . . · (x - x 3) x 2 + p x + q, where x 2 + p x + q = (x - x 1) (x - x 2) .

Comment

The roots of a polynomial can be repeated. Let's consider the proof of the algebra theorem, a consequence of Bezout's theorem.

Fundamental theorem of algebra

Theorem 2

Any polynomial with degree n has at least one root.

Bezout's theorem

After dividing a polynomial of the form P n x = a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 on (x - s), then we get the remainder, which is equal to the polynomial at point s, then we get

P n x = a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = (x - s) · Q n - 1 (x) + P n (s) , where Q n - 1 (x) is a polynomial with degree n - 1.

Corollary to Bezout's theorem

When the root of the polynomial P n (x) is considered to be s, then P n x = a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = (x - s) · Q n - 1 (x) . This corollary is sufficient when used to describe the solution.

Factoring a quadratic trinomial

A square trinomial of the form a x 2 + b x + c can be factorized into linear factors. then we get that a x 2 + b x + c = a (x - x 1) (x - x 2) , where x 1 and x 2 are roots (complex or real).

This shows that the expansion itself reduces to solving the quadratic equation subsequently.

Example 1

Factor the quadratic trinomial.

Solution

It is necessary to find the roots of the equation 4 x 2 - 5 x + 1 = 0. To do this, you need to find the value of the discriminant using the formula, then we get D = (- 5) 2 - 4 · 4 · 1 = 9. From here we have that

x 1 = 5 - 9 2 4 = 1 4 x 2 = 5 + 9 2 4 = 1

From this we get that 4 x 2 - 5 x + 1 = 4 x - 1 4 x - 1.

To perform the check, you need to open the parentheses. Then we get an expression of the form:

4 x - 1 4 x - 1 = 4 x 2 - x - 1 4 x + 1 4 = 4 x 2 - 5 x + 1

After checking, we arrive at the original expression. That is, we can conclude that the decomposition was performed correctly.

Example 2

Factor the quadratic trinomial of the form 3 x 2 - 7 x - 11 .

Solution

We find that it is necessary to calculate the resulting quadratic equation of the form 3 x 2 - 7 x - 11 = 0.

To find the roots, you need to determine the value of the discriminant. We get that

3 x 2 - 7 x - 11 = 0 D = (- 7) 2 - 4 3 (- 11) = 181 x 1 = 7 + D 2 3 = 7 + 181 6 x 2 = 7 - D 2 3 = 7 - 181 6

From this we get that 3 x 2 - 7 x - 11 = 3 x - 7 + 181 6 x - 7 - 181 6.

Example 3

Factor the polynomial 2 x 2 + 1.

Solution

Now we need to solve the quadratic equation 2 x 2 + 1 = 0 and find its roots. We get that

2 x 2 + 1 = 0 x 2 = - 1 2 x 1 = - 1 2 = 1 2 i x 2 = - 1 2 = - 1 2 i

These roots are called complex conjugate, which means the expansion itself can be depicted as 2 x 2 + 1 = 2 x - 1 2 · i x + 1 2 · i.

Example 4

Decompose the quadratic trinomial x 2 + 1 3 x + 1 .

Solution

First you need to solve a quadratic equation of the form x 2 + 1 3 x + 1 = 0 and find its roots.

x 2 + 1 3 x + 1 = 0 D = 1 3 2 - 4 1 1 = - 35 9 x 1 = - 1 3 + D 2 1 = - 1 3 + 35 3 i 2 = - 1 + 35 · i 6 = - 1 6 + 35 6 · i x 2 = - 1 3 - D 2 · 1 = - 1 3 - 35 3 · i 2 = - 1 - 35 · i 6 = - 1 6 - 35 6 · i

Having obtained the roots, we write

x 2 + 1 3 x + 1 = x - - 1 6 + 35 6 i x - - 1 6 - 35 6 i = = x + 1 6 - 35 6 i x + 1 6 + 35 6 i

Comment

If the discriminant value is negative, then the polynomials will remain second-order polynomials. It follows from this that we will not expand them into linear factors.

Methods for factoring a polynomial of degree higher than two

When decomposing, a universal method is assumed. Most of all cases are based on a corollary of Bezout's theorem. To do this, you need to select the value of the root x 1 and reduce its degree by dividing by a polynomial by 1 by dividing by (x - x 1). The resulting polynomial needs to find the root x 2, and the search process is cyclical until we obtain a complete expansion.

If the root is not found, then other methods of factorization are used: grouping, additional terms. This topic posits a solution to the equations with higher degrees and integer coefficients.

Taking the common factor out of brackets

Consider the case when the free term is equal to zero, then the form of the polynomial becomes P n (x) = a n x n + a n - 1 x n - 1 + . . . + a 1 x .

It can be seen that the root of such a polynomial will be equal to x 1 = 0, then the polynomial can be represented as the expression P n (x) = a n x n + a n - 1 x n - 1 +. . . + a 1 x = = x (a n x n - 1 + a n - 1 x n - 2 + . . . + a 1)

This method is considered to be taking the common factor out of brackets.

Example 5

Factor the third degree polynomial 4 x 3 + 8 x 2 - x.

Solution

We see that x 1 = 0 is the root of the given polynomial, then we can remove x from the brackets of the entire expression. We get:

4 x 3 + 8 x 2 - x = x (4 x 2 + 8 x - 1)

Let's move on to finding the roots of the square trinomial 4 x 2 + 8 x - 1. Let's find the discriminant and roots:

D = 8 2 - 4 4 (- 1) = 80 x 1 = - 8 + D 2 4 = - 1 + 5 2 x 2 = - 8 - D 2 4 = - 1 - 5 2

Then it follows that

4 x 3 + 8 x 2 - x = x 4 x 2 + 8 x - 1 = = 4 x x - - 1 + 5 2 x - - 1 - 5 2 = = 4 x x + 1 - 5 2 x + 1 + 5 2

To begin with, let us take into consideration a decomposition method containing integer coefficients of the form P n (x) = x n + a n - 1 x n - 1 + . . . + a 1 x + a 0, where the coefficient of the highest degree is 1.

When a polynomial has integer roots, then they are considered divisors of the free term.

Example 6

Expand the expression f (x) = x 4 + 3 x 3 - x 2 - 9 x - 18.

Solution

Let's consider whether there are complete roots. It is necessary to write down the divisors of the number - 18. We get that ±1, ±2, ±3, ±6, ±9, ±18. It follows that this polynomial has integer roots. You can check using Horner's scheme. It is very convenient and allows you to quickly obtain the expansion coefficients of a polynomial:

It follows that x = 2 and x = - 3 are the roots of the original polynomial, which can be represented as a product of the form:

f (x) = x 4 + 3 x 3 - x 2 - 9 x - 18 = (x - 2) (x 3 + 5 x 2 + 9 x + 9) = = (x - 2) (x + 3) (x 2 + 2 x + 3)

We proceed to the expansion of a quadratic trinomial of the form x 2 + 2 x + 3.

Since the discriminant is negative, it means there are no real roots.

Answer: f (x) = x 4 + 3 x 3 - x 2 - 9 x - 18 = (x - 2) (x + 3) (x 2 + 2 x + 3)

Comment

It is allowed to use root selection and division of a polynomial by a polynomial instead of Horner's scheme. Let's move on to considering the expansion of a polynomial containing integer coefficients of the form P n (x) = x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 , the highest of which is equal to one.

This case occurs for rational fractions.

Example 7

Factorize f (x) = 2 x 3 + 19 x 2 + 41 x + 15 .

Solution

It is necessary to replace the variable y = 2 x, you should move on to a polynomial with coefficients equal to 1 at the highest degree. You need to start by multiplying the expression by 4. We get that

4 f (x) = 2 3 x 3 + 19 2 2 x 2 + 82 2 x + 60 = = y 3 + 19 y 2 + 82 y + 60 = g (y)

When the resulting function of the form g (y) = y 3 + 19 y 2 + 82 y + 60 has integer roots, then their location is among the divisors of the free term. The entry will look like:

±1, ±2, ±3, ±4, ±5, ±6, ±10, ±12, ±15, ±20, ±30, ±60

Let's move on to calculating the function g (y) at these points in order to get zero as a result. We get that

g (1) = 1 3 + 19 1 2 + 82 1 + 60 = 162 g (- 1) = (- 1) 3 + 19 (- 1) 2 + 82 (- 1) + 60 = - 4 g (2) = 2 3 + 19 2 2 + 82 2 + 60 = 308 g (- 2) = (- 2) 3 + 19 (- 2) 2 + 82 (- 2) + 60 = - 36 g (3) = 3 3 + 19 3 2 + 82 3 + 60 = 504 g (- 3) = (- 3) 3 + 19 (- 3) 2 + 82 (- 3) + 60 = - 42 g (4) = 4 3 + 19 · 4 2 + 82 · 4 + 60 = 756 g (- 4) = (- 4) 3 + 19 · (- 4) 2 + 82 · (- 4) + 60 = - 28 g (5) = 5 3 + 19 5 2 + 82 5 + 60 = 1070 g (- 5) = (- 5) 3 + 19 (- 5) 2 + 82 (- 5) + 60

We find that y = - 5 is the root of an equation of the form y 3 + 19 y 2 + 82 y + 60, which means x = y 2 = - 5 2 is the root of the original function.

Example 8

It is necessary to divide with a column 2 x 3 + 19 x 2 + 41 x + 15 by x + 5 2.

Solution

Let's write it down and get:

2 x 3 + 19 x 2 + 41 x + 15 = x + 5 2 (2 x 2 + 14 x + 6) = = 2 x + 5 2 (x 2 + 7 x + 3)

Checking the divisors will take a lot of time, so it is more profitable to factorize the resulting quadratic trinomial of the form x 2 + 7 x + 3. By equating to zero we find the discriminant.

x 2 + 7 x + 3 = 0 D = 7 2 - 4 1 3 = 37 x 1 = - 7 + 37 2 x 2 = - 7 - 37 2 ⇒ x 2 + 7 x + 3 = x + 7 2 - 37 2 x + 7 2 + 37 2

It follows that

2 x 3 + 19 x 2 + 41 x + 15 = 2 x + 5 2 x 2 + 7 x + 3 = = 2 x + 5 2 x + 7 2 - 37 2 x + 7 2 + 37 2

Artificial techniques for factoring a polynomial

Rational roots are not inherent in all polynomials. To do this, you need to use special methods to find factors. But not all polynomials can be expanded or represented as a product.

Grouping method

There are cases when you can group the terms of a polynomial to find a common factor and put it out of brackets.

Example 9

Factor the polynomial x 4 + 4 x 3 - x 2 - 8 x - 2.

Solution

Because the coefficients are integers, then the roots can presumably also be integers. To check, take the values ​​1, - 1, 2 and - 2 in order to calculate the value of the polynomial at these points. We get that

1 4 + 4 1 3 - 1 2 - 8 1 - 2 = - 6 ≠ 0 (- 1) 4 + 4 (- 1) 3 - (- 1) 2 - 8 (- 1) - 2 = 2 ≠ 0 2 4 + 4 2 3 - 2 2 - 8 2 - 2 = 26 ≠ 0 (- 2) 4 + 4 (- 2) 3 - (- 2) 2 - 8 (- 2) - 2 = - 6 ≠ 0

This shows that there are no roots; it is necessary to use another method of expansion and solution.

It is necessary to group:

x 4 + 4 x 3 - x 2 - 8 x - 2 = x 4 + 4 x 3 - 2 x 2 + x 2 - 8 x - 2 = = (x 4 - 2 x 2) + (4 x 3 - 8 x) + x 2 - 2 = = x 2 (x 2 - 2) + 4 x (x 2 - 2) + x 2 - 2 = = (x 2 - 2) (x 2 + 4 x + 1)

After grouping the original polynomial, you need to represent it as the product of two square trinomials. To do this we need to factorize. we get that

x 2 - 2 = 0 x 2 = 2 x 1 = 2 x 2 = - 2 ⇒ x 2 - 2 = x - 2 x + 2 x 2 + 4 x + 1 = 0 D = 4 2 - 4 1 1 = 12 x 1 = - 4 - D 2 1 = - 2 - 3 x 2 = - 4 - D 2 1 = - 2 - 3 ⇒ x 2 + 4 x + 1 = x + 2 - 3 x + 2 + 3

x 4 + 4 x 3 - x 2 - 8 x - 2 = x 2 - 2 x 2 + 4 x + 1 = = x - 2 x + 2 x + 2 - 3 x + 2 + 3

Comment

The simplicity of grouping does not mean that choosing terms is easy enough. There is no specific solution method, so it is necessary to use special theorems and rules.

Example 10

Factor the polynomial x 4 + 3 x 3 - x 2 - 4 x + 2 .

Solution

The given polynomial has no integer roots. The terms should be grouped. We get that

x 4 + 3 x 3 - x 2 - 4 x + 2 = = (x 4 + x 3) + (2 x 3 + 2 x 2) + (- 2 x 2 - 2 x) - x 2 - 2 x + 2 = = x 2 (x 2 + x) + 2 x (x 2 + x) - 2 (x 2 + x) - (x 2 + 2 x - 2) = = (x 2 + x) (x 2 + 2 x - 2) - (x 2 + 2 x - 2) = (x 2 + x - 1) (x 2 + 2 x - 2)

After factorization we get that

x 4 + 3 x 3 - x 2 - 4 x + 2 = x 2 + x - 1 x 2 + 2 x - 2 = = x + 1 + 3 x + 1 - 3 x + 1 2 + 5 2 x + 1 2 - 5 2

Using abbreviated multiplication formulas and Newton's binomial to factor a polynomial

Appearance often does not always make it clear which method should be used during decomposition. After the transformations have been made, you can build a line consisting of Pascal’s triangle, otherwise they are called Newton’s binomial.

Example 11

Factor the polynomial x 4 + 4 x 3 + 6 x 2 + 4 x - 2.

Solution

It is necessary to convert the expression to the form

x 4 + 4 x 3 + 6 x 2 + 4 x - 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 - 3

The sequence of coefficients of the sum in parentheses is indicated by the expression x + 1 4 .

This means we have x 4 + 4 x 3 + 6 x 2 + 4 x - 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 - 3 = x + 1 4 - 3.

After applying the difference of squares, we get

x 4 + 4 x 3 + 6 x 2 + 4 x - 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 - 3 = x + 1 4 - 3 = = x + 1 4 - 3 = x + 1 2 - 3 x + 1 2 + 3

Consider the expression that is in the second bracket. It is clear that there are no knights there, so we should apply the difference of squares formula again. We get an expression of the form

x 4 + 4 x 3 + 6 x 2 + 4 x - 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 - 3 = x + 1 4 - 3 = = x + 1 4 - 3 = x + 1 2 - 3 x + 1 2 + 3 = = x + 1 - 3 4 x + 1 + 3 4 x 2 + 2 x + 1 + 3

Example 12

Factorize x 3 + 6 x 2 + 12 x + 6 .

Solution

Let's start transforming the expression. We get that

x 3 + 6 x 2 + 12 x + 6 = x 3 + 3 2 x 2 + 3 2 2 x + 2 3 - 2 = (x + 2) 3 - 2

It is necessary to apply the formula for abbreviated multiplication of the difference of cubes. We get:

x 3 + 6 x 2 + 12 x + 6 = = (x + 2) 3 - 2 = = x + 2 - 2 3 x + 2 2 + 2 3 x + 2 + 4 3 = = x + 2 - 2 3 x 2 + x 2 + 2 3 + 4 + 2 2 3 + 4 3

A method for replacing a variable when factoring a polynomial

When replacing a variable, the degree is reduced and the polynomial is factored.

Example 13

Factor the polynomial of the form x 6 + 5 x 3 + 6 .

Solution

According to the condition, it is clear that it is necessary to make the replacement y = x 3. We get:

x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6

The roots of the resulting quadratic equation are y = - 2 and y = - 3, then

x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3

It is necessary to apply the formula for abbreviated multiplication of the sum of cubes. We get expressions of the form:

x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3 = = x + 2 3 x 2 - 2 3 x + 4 3 x + 3 3 x 2 - 3 3 x + 9 3

That is, we obtained the desired decomposition.

The cases discussed above will help in considering and factoring a polynomial in different ways.

If you notice an error in the text, please highlight it and press Ctrl+Enter

Plan - lesson notes (MBOU "Chernomorskaya high school No. 2"

Teacher's name

Ponomarenko Vladislav Vadimovich

Item

Algebra

Lesson date

19.09.2018

№ lesson

Class

9B

Lesson topic

(in accordance with KTP)

"Decomposition quadratic trinomial by multipliers"

Goal setting

- educational: teach students how to factor a square trinomial, teach how to use the algorithm for factoring a square trinomial when solving examples, consider tasks in the GIA database that use the algorithm for factoring a square trinomial

-developing: develop in schoolchildren the ability to formulate problems, propose ways to solve them, and promote the development in schoolchildren of the ability to highlight the main thing in a cognitive object.

-educational: to help students realize the value of joint activities, to promote the development in children of the ability to exercise self-control, self-esteem and self-correction of educational activities.

Lesson type

studying and primary consolidation of new knowledge.

Equipment:

multimedia projector, screen, computer, didactic material, textbooks, notebooks, presentationfor the lesson

Lesson progress

1. Organizational moment: The teacher greets the students and checks their readiness for the lesson.

Motivates students:

Today in our lesson, in a joint activity, we will confirm the words of Polya (Slide 1). (“The problem you solve may be very modest, but if it challenges your curiosity, and if you solve it on your own, then you can experience the leading to open the tension of the mind and enjoy the joy of victory."

Message about Poya (Slide 2)

I want to challenge your curiosity. Let's consider the task from the State Inspectorate. Graph the Function .

Can we enjoy the joy of victory and complete this task? (problematic situation).

How to solve this problem?

- Outline an action plan to solve this problem.

Corrects the lesson plan, comments on the principle of independent work.

Independent work(distribute leaflets with the text of independent work to the class) (Appendix 1)

Independent work

Factor it out:

x 2 – 3x;

x 2 – 9;

x 2 – 8x + 16;

2a 2 – 2b 2 –a + b;

2x 2 – 7x – 4.

Reduce a fraction:

SlideWith answers for self-test.

Question for the class:

What methods of factoring a polynomial have you used?

Were you able to factor all the polynomials?

Were you able to reduce all the fractions?

Problem2:Slide

How to factor a polynomial

2 x 2 – 7 x – 4?

How to reduce a fraction?

Frontal survey:

What are polynomials

2 x 2 – 7 x– 4 andx 2 – 5 x +6?

Give the definition of a quadratic trinomial.

What do we know about the quadratic trinomial?

How to find its roots?

What determines the number of roots?

Compare this knowledge with what we need to learn and formulate the topic of the lesson. (After this, the topic of the lesson appears on the screen)Slide

Let's set the goal of the lessonSlide

Let's outline the final resultSlide

Question to the class:How to solve this problem?

The class works in groups.

Group assignment:

Use the table of contents to find the page you need, read paragraph 4 with a pencil in your hands, highlight the main idea, create an algorithm by which any square trinomial can be factorized.

Checking the completion of the task by the class (front work):

What is main idea point 4?Slide(on the screen is the formula for factoring a quadratic trinomial).

Algorithm on the screen.Slide

1. Equate the quadratic trinomial to zero.

2. Find the discriminant.

3. Find the roots of the quadratic trinomial.

4.Substitute the found roots into the formula.

5.If necessary, enter the leading coefficient in brackets.

One moresmall problem : if D=0, then is it possible to factorize a quadratic trinomial, and if so, how?

(Research work in groups).

Slide(on screen:

If D = 0, then
.

If a quadratic trinomial has no roots,

then it cannot be factorized.)

Let's return to the task in independent work. Can we now factor quadratic trinomials?2 x 2 – 7 x– 4 andx 2 – 5 x +6?

The class works independently, factorizes, I work individually with weak students.

Slide(with solution)Peer review

Can we reduce the fraction?

To reduce the fraction, I call a strong student to the board.

Let's get back to the taskfrom GIA. Can we now graph the function?

What is the graph of this function?

Draw a graph of the function in your notebook.

Test (Withindependent work)Appendix 2

Self-test and self-assessmentStudents were given sheets of paper (Appendix 3) on which to write down their answers. They provide evaluation criteria.

Evaluation criteria:

3 tasks - assessment"4"

4 tasks – score “5”

Reflection:(slide)

1.Today in class I learned...

2.Today in class I repeated...

3.I secured...

4.I liked it...

5. I gave myself a grade for my activities in class...

6.What types of work caused difficulties and require repetition...

7. Have we achieved the intended result?

Slide: Thanks for the lesson!

Appendix 1

Independent work

Factor it out:

x 2 – 3x;

x 2 – 9;

x 2 – 8x + 16;

x 2 + x - 2;

2a 2 – 2b 2 –a + b;

2 x 2 – 7 x – 4.

Reduce a fraction:

Appendix 2

Test

1 option

multiply?

x 2 – 8x+ 7;

x 2 – 8x+ 16 ;

x 2 – 8x+ 9;

x 2 – 8x+ 1 7.

2 x 2 – 9 x – 5 = 2( x – 5)(…)?

Answer:_________ .

Reduce the fraction:

x – 3;

x + 3;

x – 4;

another answer.

Test

Option 2

Which quadratic trinomial cannot be pmultiply?

5 x 2 + x+ 1;

⅓ x 2 –8x+ 2;

0,1 x 2 + 3 x - 5;

x 2 + 4 x+ 5.

What polynomial should be substituted for the ellipsis to create equality:2 x 2 + 5 x – 3 = 2( x + 3)(…)?

Answer:_________ .

Reduce the fraction:

3 x 2 – 6 x – 15;

0,25(3 x - 1);

0,25( x - 1);

another answer.

Appendix 3

Write down your answers.

Evaluation criteria:

Completed correctly: task 2 – score “3”

3 tasks - assessment"4"

4 tasks – score “5”

Task No. 1

Task No. 2

Task No. 3

1 option

Option 2

Factoring quadratic trinomials refers to school assignments that everyone faces sooner or later. How to do it? What is the formula for factoring a quadratic trinomial? Let's figure it out step by step using examples.

General formula

Quadratic trinomials are factorized by solving a quadratic equation. This is a simple problem that can be solved by several methods - by finding the discriminant using Vieta's theorem, there is also a graphical solution. The first two methods are studied in high school.

The general formula looks like this:lx 2 +kx+n=l(x-x 1)(x-x 2) (1)

Algorithm for completing the task

In order to factor quadratic trinomials, you need to know Vita's theorem, have a solution program at hand, be able to find a solution graphically, or look for the roots of a second-degree equation using the discriminant formula. If a quadratic trinomial is given and it needs to be factorized, the algorithm is as follows:

1) Equate the original expression to zero to obtain an equation.

2) Give similar terms (if necessary).

3) Find the roots using any known method. The graphical method is best used if it is known in advance that the roots are integers and small numbers. It must be remembered that the number of roots is equal to the maximum degree of the equation, that is, the quadratic equation has two roots.

4) Substitute the value X into expression (1).

5) Write down the factorization of quadratic trinomials.

Examples

Practice allows you to finally understand how this task is performed. The following examples illustrate the factorization of a quadratic trinomial:

it is necessary to expand the expression:

Let's resort to our algorithm:

1) x 2 -17x+32=0

2) similar terms are reduced

3) using Vieta’s formula, it is difficult to find roots for this example, so it is better to use the expression for the discriminant:

D=289-128=161=(12.69) 2

4) Let’s substitute the roots we found into the basic formula for decomposition:

(x-2.155) * (x-14.845)

5) Then the answer will be like this:

x 2 -17x+32=(x-2.155)(x-14.845)

Let's check whether the solutions found by the discriminant correspond to the Vieta formulas:

14,845 . 2,155=32

For these roots, Vieta’s theorem is applied, they were found correctly, which means the factorization we obtained is also correct.

Let us similarly expand 12x 2 + 7x-6.

x 1 =-7+(337) 1/2

x 2 =-7-(337)1/2

In the previous case, the solutions were non-integer, but real numbers, which are easy to find if you have a calculator in front of you. Now let's look at more complex example, in which the roots will be complex: factor x 2 + 4x + 9. Using Vieta's formula, the roots cannot be found, and the discriminant is negative. The roots will be on the complex plane.

D=-20

Based on this, we obtain the roots that interest us -4+2i*5 1/2 and -4-2i * 5 1/2 since (-20) 1/2 = 2i*5 1/2 .

We obtain the desired decomposition by substituting the roots into the general formula.

Another example: you need to factor the expression 23x 2 -14x+7.

We have the equation 23x 2 -14x+7 =0

D=-448

This means the roots are 14+21.166i and 14-21.166i. The answer will be:

23x 2 -14x+7 =23(x- 14-21,166i )*(X- 14+21,166i ).

Let us give an example that can be solved without the help of a discriminant.

Let's say we need to expand the quadratic equation x 2 -32x+255. Obviously, it can also be solved using a discriminant, but in this case it is faster to find the roots.

x 1 =15

x 2 =17

Means x 2 -32x+255 =(x-15)(x-17).