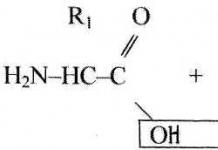
1. Van der Waalsova chemical bond characteristic of electrically neutral atoms that do not have an electric dipole moment.

The force of attraction is called the dispersion force.

For polar systems with a constant dipole moment, the van der Waals orientational mechanism of chemical bonding predominates.

Molecules with high polarization are characterized by an induced electric moment when the molecules approach each other by enough close quarters. In the general case, all three types of the Van der Waals chemical bond mechanism can occur, which is weaker than all other types of chemical bond by two to three orders of magnitude.

The total energy of interaction of molecules with a chemical bond Van - der - Waals, is equal to the sum of the energies of dispersion, orientation and induced interactions.

2. Ionic (heteropolar) chemical bond occurs when one atom is able to transfer one or more electrons to another atom.

As a result, positively and negatively charged ions appear, between which a dynamic equilibrium is established. Such a bond is characteristic of halides and alkali metals. The dependence W p (r) for molecules with an ionic bond is shown in Fig. . 8.1. The distance r 0 corresponds to the minimum potential energy.

3. Covalent (homeopolar) chemical bond or atomic bond occurs when atoms with similar properties interact.

When interacting, states with increased density appear electron cloud and the emergence of exchange energy.

Quantum theory shows that the exchange energy is a consequence of the identity of closely spaced particles.

characteristic feature atomic bond is its saturation, i.e., each atom is able to form a limited number of bonds.

4. In a metallic chemical bond all atoms of the crystal participate, and the socialized electrons move freely within the entire lattice of the crystal.

Hydrogen molecule

The hydrogen molecule is bound by forces that lead to this bond; they are exchange forces, i.e., a quantum approach is required for consideration.

Using the theory of perturbations Geytler and F. London in 1927 solved in an approximate variant.

AT quantum mechanics the problem of a hydrogen molecule is reduced to solving the Schrödinger equation for a stationary state.

Using the adiabatic approximation, i.e., consider the wave function as a function of only the coordinates of electrons, and not of atomic nuclei.

The total wave function depends not only on the spatial coordinates of the electrons, but also on their spins and is antisymmetric.

If we take into account only the wave function of the electron, the problem can be solved if we take into account 2 cases:

1. The spin wave function is antisymmetric, and the spatial wave function is symmetric, and the total spin of two electrons is equal to zero (singlet state).

2. The spin wave function is symmetric, and the spatial wave function is antisymmetric, and the total spin of two electrons is equal to unity and can be oriented by three different ways(triplet state).

In the symmetric state, when the spin wave function is antisymmetric and in the zeroth approximation, a symmetric spatial wave function with separable variables is obtained.

In the triplet state, when the spin wave function is symmetric, an antisymmetric spatial wave function is obtained.

Due to the identity of the electrons, an exchange interaction arises, which manifests itself in calculations due to the use of symmetric and antisymmetric spatial wave functions.

When atoms in the singlet spin state approach each other (the spins are antiparallel), the interaction energy first decreases and then rapidly increases. In the triplet spin state (the spins are parallel), the energy minimum does not occur.

The equilibrium position of the atom exists only in the singlet spin state, when the energy is reduced to a minimum. It is only in this state that the formation of a hydrogen atom is possible.

Molecular spectra

Molecular spectra arise as a result of quantum transitions between the energy levels W* and W** of molecules according to the relation

hn = W * - W ** , (1)

where hn is the energy of the emitted or absorbed quantum of frequency n.

Molecular spectra are more complex than atomic spectra, which is determined by the internal motion in molecules.

Since, in addition to the movement of electrons relative to two or more nuclei in a molecule, there are oscillatory the motion of the nuclei (together with the inner electrons surrounding them) about the positions of equilibrium and rotational molecular movements.

Three types of energy levels correspond to the electronic, vibrational and rotational motions of molecules:

W e , W count and W vr,

and three types of molecular spectra.

According to quantum mechanics, the energies of all types of molecular motions can only take on certain values ​​(except for the energy of translational motion).

The energy of the molecule W, the change of which determines the molecular spectrum, can be represented as the sum of the quantum values ​​of the energies:

W \u003d W e + W count + W vr, (2)

and in order of magnitude:

W e: W count: W vr \u003d 1:.

Consequently,

W e >> W count >> W temp.

DW = DW * - DW ** = DW e + DW count + DW temp. (3)

The electron energy W e is of the order of several electron volts:

W count » 10 - 2 - 10 - 1 eV, W vr » 10 - 5 - 10 - 3 eV.

The system of energy levels of molecules is characterized by a set of electronic energy levels far apart from each other.

Vibrational levels are much closer to each other, and the rotational energy levels are even closer to each other.

Typical molecular spectra-sets of narrow bands (consisting of a large number individual lines) of various widths in the UV, visible and IR regions of the spectrum, clear from one edge and blurry from the other.

Energy levels a and b correspond to equilibrium configurations of 2 molecules (Fig. 2).

Each electronic state corresponds to a certain energy value W e - smallest value, the ground electronic state (the main electronic energy level of the molecule).

The set of electronic states of a molecule is determined by the properties of its electron shell.

Vibrational energy levels

Vibrational energy levels can be found by quantizing the oscillatory motion, which is approximately considered harmonic.

A diatomic molecule (one vibrational degree of freedom corresponding to a change in the internuclear distance r) can be considered as a harmonic oscillator whose quantization gives equidistant energy levels:

, (4)

where n is the fundamental frequency of harmonic vibrations of the molecule;

v count = 0, 1, 2, ... - vibrational quantum number.

Rotational energy levels

Rotational energy levels can be found by quantizing rotary motion molecules, considering it as solid with a certain moment of inertia I.

In the case of a diatomic or linear triatomic molecule, its rotational energy

where I is the moment of inertia of the molecule about the axis perpendicular to the axis of the molecule; L is the angular momentum.

According to the quantization rules

, (6)

where J = 0, 1, 2, 3, ... is the rotational quantum number.

For rotational energy we get

, (7)

The rotational constant determines the scale of the distance between energy levels.

The variety of molecular spectra is due to the difference in the types of transitions between the energy levels of molecules.

The main task of theories chemical kinetics- propose a method for calculating the rate constant of an elementary reaction and its dependence on temperature, using different ideas about the structure of the reagents and the reaction path. We will consider two simplest theories of kinetics - the theory of active collisions (TAC) and the theory activated complex(SO).

Theory of active collisions is based on counting the number of collisions between reacting particles, which are represented as hard spheres. It is assumed that the collision will lead to a reaction if two conditions are met: 1) the translational energy of the particles exceeds the activation energy E A; 2) the particles are correctly oriented in space relative to each other. The first condition introduces the factor exp(- E A/RT), which is equal to percentage of active collisions in the total number of collisions. The second condition gives the so-called steric factor P- a constant characteristic of this reaction.

The TAS has obtained two basic expressions for the rate constant of a bimolecular reaction. For a reaction between different molecules(A + B products) the rate constant is

Here N A is the Avogadro constant, r are the radii of the molecules, M- molar masses of substances. The multiplier in large parentheses is the average speed relative motion particles A and B.

The rate constant of a bimolecular reaction between identical molecules (2A products) is:

(9.2)

From (9.1) and (9.2) it follows that the temperature dependence of the rate constant has the form:

.

According to TAS, the pre-exponential factor depends only slightly on temperature. Experienced activation energy E op, determined by equation (4.4), is related to the Arrhenius, or true activation energy E A ratio:

E op = E A - RT/2.

Monomolecular reactions within TAS are described using the Lindemann scheme (see Problem 6.4), in which the activation rate constant k 1 is calculated by formulas (9.1) and (9.2).

AT activated complex theory an elementary reaction is represented as a monomolecular decomposition of an activated complex according to the scheme:

It is assumed that there is a quasi-equilibrium between the reactants and the activated complex. The rate constant of monomolecular decomposition is calculated by the methods of statistical thermodynamics, representing the decomposition as a one-dimensional translational motion of the complex along the reaction coordinate.

The basic equation of the activated complex theory is:

, (9.3)

where k B= 1.38 . 10 -23 J/K - Boltzmann's constant, h= 6.63 . 10 -34 J. s - Planck's constant, - equilibrium constant for the formation of an activated complex, expressed in terms of molar concentrations (in mol / l). Depending on how the equilibrium constant is estimated, there are statistical and thermodynamic aspects of SO.

AT statistical approach, the equilibrium constant is expressed in terms of sums over states:

, (9.4)

where is the total sum over the states of the activated complex, Q react is the product of the total sums over the states of the reactants, is the activation energy at absolute zero, T = 0.

The total sums over states are usually decomposed into factors corresponding to certain types of molecular motion: translational, electronic, rotational and vibrational:

Q = Q fast. Q email . Q temp. . Q count

Translational sum over states for a particle of mass m is equal to:

Q post = .

This translational amount has the dimension (volume) -1, because through it the concentrations of substances are expressed.

The electronic sum over states at ordinary temperatures is, as a rule, constant and equal to the degeneracy of the ground electronic state: Q email = g 0 .

The rotational sum over states for a diatomic molecule is:

Q vr = ,

where m = m 1 m 2 / (m 1 +m 2) is the reduced mass of the molecule, r- internuclear distance, s = 1 for asymmetric molecules AB and s =2 for symmetrical molecules A 2 . For linear polyatomic molecules, the rotational sum over states is proportional to T, and for nonlinear molecules - T 3/2. At ordinary temperatures, rotational sums over states are of the order of 10 1 -10 2 .

The vibrational sum over the states of a molecule is written as a product of factors, each of which corresponds to a certain vibration:

Q count = ,

where n- number of vibrations (for a linear molecule consisting of N atoms, n = 3N-5, for non-linear molecule n = 3N-6), c= 3 . 10 10 cm/s - speed of light, n i- oscillation frequencies, expressed in cm -1 . At ordinary temperatures, the vibrational sums over states are very close to 1 and noticeably differ from it only under the condition: T>n. At very high temperatures, the vibrational sum for each vibration is directly proportional to the temperature:

Q i .

The difference between an activated complex and ordinary molecules is that it has one less vibrational degree of freedom, namely: the vibration that leads to the decomposition of the complex is not taken into account in the vibrational sum over states.

AT thermodynamic approach, the equilibrium constant is expressed in terms of the difference between the thermodynamic functions of the activated complex and the initial substances. For this, the equilibrium constant expressed in terms of concentrations is converted into a constant expressed in terms of pressures. The last constant is known to be related to the change in the Gibbs energy in the reaction of the formation of an activated complex:

.

For a monomolecular reaction in which the formation of an activated complex occurs without changing the number of particles, = and the rate constant is expressed as follows:

Entropy factor exp ( S /R) is sometimes interpreted as a steric factor P from the theory of active collisions.

For a bimolecular reaction occurring in the gas phase, a factor is added to this formula RT / P 0 (where P 0 \u003d 1 atm \u003d 101.3 kPa), which is needed to go from to:

For a bimolecular reaction in solution, the equilibrium constant is expressed in terms of the Helmholtz energy of formation of the activated complex:

Example 9-1. Bimolecular reaction rate constant

2NO2 2NO + O2

at 627 K is 1.81. 10 3 cm 3 / (mol. s). Calculate the true activation energy and the proportion of active molecules, if the diameter of the NO 2 molecule can be taken equal to 3.55 A, and the steric factor for this reaction is 0.019.

Decision. In the calculation, we will rely on the theory of active collisions (formula (9.2)):

.

This number represents the proportion of active molecules.

When calculating the rate constants using various theories of chemical kinetics, one must be very careful with the dimensions. Note that the radius of the molecule and average speed expressed in cm to give a constant in cm 3 /(mol. s). The factor 100 is used to convert m/s to cm/s.

The true activation energy can be easily calculated in terms of the fraction of active molecules:

J/mol = 166.3 kJ/mol.

Example 9-2. Using the activated complex theory, determine the temperature dependence of the rate constant of the trimolecular reaction 2NO + Cl 2 = 2NOCl at temperatures close to room temperature. Find the connection between experienced and true activation energies.

Decision. According to the statistical variant SO, the rate constant is (formula (9.4)):

.

In the sums over the states of the activated complex and reagents, we will not take into account the vibrational and electronic degrees of freedom, since at low temperatures, the vibrational sums over states are close to unity, while the electronic sums are constant.

The temperature dependences of the sums over the states, taking into account the translational and rotational motions, have the form:

The activated complex (NO) 2 Cl 2 is a nonlinear molecule, therefore its rotational sum over states is proportional to T 3/2 .

Substituting these dependencies into the expression for the rate constant, we find:

We see that trimolecular reactions are characterized by a rather unusual dependence of the rate constant on temperature. Under certain conditions, the rate constant can even decrease with increasing temperature due to the pre-exponential factor!

The experimental activation energy of this reaction is:

.

Example 9-3. Using the statistical version of the activated complex theory, obtain an expression for the rate constant of a monomolecular reaction.

Decision. For a monomolecular reaction

A AN products

the rate constant, according to (9.4), has the form:

.

An activated complex in a monomolecular reaction is an excited reactant molecule. The translational sums of the reagent A and the complex AN are the same (the mass is the same). If we assume that the reaction occurs without electronic excitation, then the electronic sums over states are the same. If we assume that the structure of the reactant molecule does not change very much upon excitation, then the rotational and vibrational sums over the states of the reactant and the complex are almost the same, with one exception: the activated complex has one less vibration than the reactant. Consequently, the vibration leading to bond cleavage is taken into account in the sum over the states of the reactant and is not taken into account in the sum over the states of the activated complex.

Carrying out the reduction of the same sums by states, we find the rate constant of a monomolecular reaction:

where n is the frequency of the oscillation that leads to the reaction. speed of light c is the multiplier that is used if the oscillation frequency is expressed in cm -1 . At low temperatures, the vibrational sum over the states is equal to 1:

.

At high temperatures the exponential in the vibrational sum over the states can be expanded into a series: exp(- x) ~ 1 - x:

.

This case corresponds to a situation where, at high temperatures, each oscillation leads to a reaction.

Example 9-4. Determine the temperature dependence of the rate constant for the reaction of molecular hydrogen with atomic oxygen:

H2+O. HO. +H. (linear activated complex)

at low and high temperatures.

Decision. According to the activated complex theory, the rate constant for this reaction is:

We assume that the electron factors do not depend on temperature. All translational sums over states are proportional T 3/2 , rotational sums over states for linear molecules are proportional to T, the vibrational sums over states at low temperatures are equal to 1, and at high temperatures they are proportional to the temperature to a degree equal to the number of vibrational degrees of freedom (3 N- 5 = 1 for H molecule 2 and 3 N- 6 = 3 for a linear activated complex). Considering all this, we find that at low temperatures

and at high temperatures

Example 9-5. The acid-base reaction in a buffer solution proceeds according to the mechanism: A - + H + P. The dependence of the rate constant on temperature is given by the expression

k = 2.05 . 10 13.e-8681/ T(l. mol -1. s -1).

Find the experimental activation energy and activation entropy at 30 o C.

Decision. Since the bimolecular reaction occurs in solution, we use expression (9.7) to calculate the thermodynamic functions. It is necessary to introduce the experimental activation energy into this expression. Since the pre-exponential factor in (9.7) depends linearly on T, then E op = + RT. Replacing in (9.7) by E oops, we get:

.

It follows that the experimental activation energy is equal to E op = 8681. R= 72140 J/mol. The activation entropy can be found from the pre-exponential factor:

,

whence = 1.49 J/(mol. K).

9-1. The diameter of the methyl radical is 3.8 A. What is the maximum rate constant (in l / (mol. s)) of the recombination of methyl radicals at 27 o C? (answer)

9-2. Calculate the value of the steric factor in the ethylene dimerization reaction

2C2H4C4H8

at 300 K, if the experimental activation energy is 146.4 kJ/mol, the effective diameter of ethylene is 0.49 nm, and the experimental rate constant at this temperature is 1.08. 10 -14 cm 3 / (mol. s).

9-7. Determine the temperature dependence of the rate constant for the reaction H . + Br 2 HBr + Br. (nonlinear activated complex) at low and high temperatures. (Answer)

9-8. For the reaction CO + O 2 = CO 2 + O, the dependence of the rate constant on temperature at low temperatures has the form:

k( T) ~ T-3/2. exp(- E 0 /RT)

(answer)

9-9. For the reaction 2NO = (NO) 2, the dependence of the rate constant on temperature at low temperatures has the form:

k( T) ~ T-1exp(- E 0/R T)

What configuration - linear or nonlinear - does the activated complex have? (Answer)

9-10. Using the active complex theory, calculate the true activation energy E 0 for reaction

CH3. + C 2 H 6 CH 4 + C 2 H 5.

at T\u003d 300 K if the experimental activation energy at this temperature is 8.3 kcal / mol. (Answer)

9-11. Derive the ratio between the experimental and true activation energies for the reaction

9-12. Determine the activation energy of a monomolecular reaction at 1000 K if the frequency of vibrations along the broken bond is n = 2.4. 10 13 s -1 , and the rate constant is k\u003d 510 min -1. (answer)

9-13. The rate constant of the reaction of the first order of decomposition of bromoethane at 500 o C is 7.3. 10 10 s -1 . Estimate the activation entropy of this reaction if the activation energy is 55 kJ/mol. (answer)

9-14. Decomposition of di-peroxide tert-butyl in the gas phase is a first order reaction whose rate constant (in s -1) depends on temperature as follows:

Using the theory of the activated complex, calculate the enthalpy and entropy of activation at a temperature of 200 o C. (answer)

9-15. The isomerization of diisopropyl ether to allylacetone in the gas phase is a first order reaction whose rate constant (in s -1) depends on temperature as follows:

Using the theory of the activated complex, calculate the enthalpy and entropy of activation at a temperature of 400 o C. (answer)

9-16. The dependence of the rate constant of decomposition of vinyl ethyl ether

C 2 H 5 -O-CH \u003d CH 2 C 2 H 4 + CH 3 CHO

temperature has the form

k = 2.7. 10 11.e -10200/ T(with -1).

Calculate the entropy of activation at 530 o C. (answer)

9-17. In the gas phase, substance A unimolecularly transforms into substance B. The rate constants of the reaction at temperatures of 120 and 140 o C are, respectively, 1.806. 10 -4 and 9.14. 10 -4 s -1 . Calculate the average entropy and heat of activation in this temperature range.

If we do not take into account the vibrational motions in the carbon dioxide molecule, then the average kinetic energy molecules is...

Decision: The average kinetic energy of a molecule is: , where is the Boltzmann constant, is the thermodynamic temperature; - the sum of the number of translational, rotational and twice the number of vibrational degrees of freedom of the molecule: . For a carbon dioxide molecule, the number of degrees of freedom of translational motion, rotational - , vibrational - , therefore, therefore, the average kinetic energy of the molecule is: .

TASK N 2 Topic: The first law of thermodynamics. Working with isoprocesses

The figure shows a diagram of the cyclic process of an ideal monatomic gas: During the cycle, the gas receives an amount of heat (in) equal to ...

Decision: The cycle consists of isochoric heating (4–1), isobaric expansion (1–2), isochoric cooling (2–3), and isobaric compression (3–4). In the first two stages of the cycle, the gas receives heat. According to the first law of thermodynamics, the amount of heat received by a gas is , where is the change in internal energy, is the work of the gas. Then . Thus, the amount of heat received by the gas per cycle is

TASK N 3 Topic: The second law of thermodynamics. Entropy

In the course of an irreversible process, when heat enters a non-isolated thermodynamic system, for the increment of entropy, the following relation will be correct: ...

Decision: The ratio in a reversible process is the total differential of the system state function, called the entropy of the system: . In isolated systems, entropy cannot decrease with any processes occurring in it: . The equal sign refers to reversible processes, and the greater than sign refers to irreversible processes. If heat enters a non-isolated system and an irreversible process occurs, then the entropy increases due not only to the received heat, but also to the irreversibility of the process: .

Task n 4 Topic: Maxwell and Boltzmann distributions

The figure shows a graph of the velocity distribution function of ideal gas molecules (Maxwell distribution), where is the fraction of molecules whose velocities are in the range of velocities from to per unit of this interval: For this function, the statements are true ...

			the position of the maximum of the curve depends not only on the temperature, but also on the nature of the gas (its molar mass)
			as the number of molecules increases, the area under the curve does not change
			with increasing gas temperature, the value of the maximum of the function increases
			for a gas with a higher molar mass (at the same temperature), the maximum of the function is located in the region of higher velocities

Decision: It follows from the definition of the Maxwell distribution function that the expression determines the proportion of molecules whose velocities are in the range of velocities from to (on the graph, this is the area of ​​the shaded strip). Then the area under the curve is and does not change with changes in temperature and the number of gas molecules. From the most probable speed formula (at which the function is maximum) it follows that is directly proportional and inversely proportional to , where and are the temperature and molar mass gas, respectively.

TASK N 5 Topic: Electrostatic field in vacuum

The figures show graphs of the field strength for various charge distributions: Dependency plot for a sphere of radius R, uniformly charged in volume, is shown in the figure ...

TASK N 6 Topic: Direct Current Laws

The figure shows the dependence of the current density j flowing in conductors 1 and 2, on the strength of the electric field E: The ratio of specific resistances r 1 / r 2 of these conductors is ...

TASK N 7 Topic: Magnetostatics

A frame with a current with a magnetic dipole moment, the direction of which is indicated in the figure, is in a uniform magnetic field: The moment of forces acting on a magnetic dipole is directed ...

			perpendicular to the plane of the picture to us
			perpendicular to the plane of the picture from us
			in the direction of the magnetic induction vector
			opposite to the magnetic induction vector

A real circuit consists of an inductor and a capacitor. A real coil cannot be considered just an inductance that stores magnetic energy. Firstly, the wire has a finite conductivity, and secondly, between the turns accumulates Electric Energy, i.e. there is an interturn capacitance. The same can be said about capacity. The real capacitance, in addition to the capacitance itself, will include lead inductances and loss resistance.

To simplify the problem, consider a model of a real oscillatory circuit with an inductor consisting of only two turns.

The equivalent circuit will have the form shown in the figure in Fig. 4. (and - inductance and resistance of one turn, - interturn capacitance).

However, as the experience of a radio engineer shows, in most cases there is no need for this complex circuit.

The equation for the electrical circuit shown in fig. 5 we obtain on the basis of Kirchhoff's law. We use the second rule: the sum of the voltage drops on the circuit elements is equal to the algebraic sum of the external EMF included in this circuit. In our case, the EMF is zero, and we get:

Divide the terms by and denote

The equation for an ideal contour will take the form:

Having models of two dynamical systems, we can already draw some conclusions.

A simple comparison of equations (B.6) and (B.9) shows that the pendulum at small deviations and the ideal circuit are described by the same equation, known as the harmonic oscillator equation, which in standard form is:

Consequently, both the pendulum and the circuit as oscillatory systems have the same properties. This is the manifestation of the unity of oscillatory systems.

Having these models, the equations that describe them, and generalizing the results obtained, we give a classification of dynamical systems according to the form differential equation. Systems are either linear or non-linear.

Linear systems are described linear equations(see (B.11) and (B.15)). Nonlinear systems are described nonlinear equations(for example, the equation of a mathematical pendulum (B.9)).

Another classification feature is number of degrees of freedom. The formal sign is the order of the differential equation describing the motion in the system. A system with one degree of freedom is described by a 2nd order equation (or two first order equations); a system with N degrees of freedom is described by an equation or a system of equations of order 2N.

Depending on how the energy of the oscillatory motion in the system changes, all systems are divided into two classes: conservative systems - those in which the energy remains unchanged, and non-conservative systems - those in which the energy changes over time. In a system with losses, the energy decreases, but there are cases when the energy increases. Such systems are called active.

A dynamic system may or may not be subject to external influences. Depending on this, four types of movement are distinguished.

1.Own, or free vibrations, systems. In this case, the system receives a finite supply of energy from an external source, and the source is turned off. The motion of the system with a finite initial supply of energy represents natural oscillations.

2.Forced vibrations. The system is under the action of an external periodic source. The source has a "force" effect, i.e. the nature of the source is the same as that of dynamic system(in mechanical system- source of power, in electrical - EMF, etc.). Oscillations caused by an external source are called forced. When disabled, they disappear.

3.Parametric vibrations are observed in systems in which some parameter changes periodically in time, for example, the capacitance in the circuit or the length of the pendulum. The nature of the external source that changes the parameter may be different from the nature of the system itself. For example, the capacitance can be changed mechanically.

It should be noted that a strict separation of forced and parametric oscillations is possible only for linear systems.

4.A special type of motion is self-oscillations. The term was first introduced by Academician Andronov. Self Oscillation- this is a periodic oscillation, the period, shape and amplitude of which depend on the internal state of the system and do not depend on the initial conditions. From the energy point of view, self-oscillatory systems are energy converters of some source into the energy of periodic oscillations.

Chapter 1. OWN OSCILLATIONS IN A LINEAR CONSERVATIVE SYSTEM WITH ONE DEGREE OF FREEDOM (HARMONIC OSCILLATOR)

The equation for such a system is:

(examples are a mathematical pendulum at small deflection angles and an ideal oscillatory circuit). We solve equation (1.1) in detail using classical method Euler. We are looking for a particular solution in the form:

where and are constants, yet unknown constants. Substitute (1.2) into equation (1.1)

We divide both parts of the equation by and we get the algebraic, so-called characteristic, equation:

The roots of this equation

where is the imaginary unit. The roots are imaginary and complex conjugate.

As is known, the general solution is the sum of the private ones, i.e.

We believe that there is a real value. For this to be true, the constants and must be complex conjugate, i.e.

Two constants and are determined from two initial conditions:

The solution in the form (1.8) is mainly used in theory; for applied problems, it is not convenient, since they are not measured. Let's move on to the form of the solution, which is most commonly used in practice. We represent the complex constants in polar form:

We substitute them into (1.8) and use the Euler formula

where is the oscillation amplitude, is the initial phase.

And are determined from the initial conditions. Note that the initial phase depends on the origin in time. Indeed, the constant can be represented as:

If the time origin coincides with , the initial phase is equal to zero. For harmonic oscillation, phase shift and time shift are equivalent.

We decompose the cosine in (1.13) into cosine and sinusoidal components. Let's get another idea:

If and are known, then it is not difficult to find the amplitude and phase of the oscillation using the following relations:

All three notations (1.8, 1.12, 1.15) are equivalent. The use of a specific form is determined by the convenience of considering a specific problem.

Analyzing the solution, one can say that the natural oscillations of a harmonic oscillator are a harmonic oscillation, the frequency of which depends on the parameters of the system and does not depend on the initial conditions; the amplitude and the initial phase depend on the initial conditions.

Independence of the frequency (period) of natural oscillations from the initial conditions is called isochoric.

Consider the energy of a harmonic oscillator using an oscillatory circuit as an example. The equation of motion in the circuit

We multiply the terms of this equation by:

After transformation, it can be represented as:

Let's find the law of change of energy in the capacitor. The current in the capacitive branch can be found using the following expression

Substituting (1.28) into the formula for finding electrical energy, we obtain the law of change in electrical energy on a capacitor

Thus, the energy in each element of the circuit oscillates at twice the frequency. The graph of these fluctuations is shown in Fig. 6.

At the initial moment of time, all the energy is concentrated in the capacitance, the magnetic energy is equal to zero. As the capacitance is discharged through the inductance, the electrical energy from the capacitance is converted into the magnetic energy of the inductor. After a quarter of the period, all the energy is concentrated in the inductance, i.e. capacity is completely discharged. This process is then repeated periodically.

Thus, an oscillation in an ideal circuit is a transition of electrical energy into magnetic energy and vice versa, periodically repeating in time.

This conclusion is valid for any electromagnetic oscillatory systems, in particular for cavity resonators, where magnetic and electrical energy are not spatially separated.

Generalizing this result, we can state that oscillatory process in a linear conservative system, it is a periodic transition of energy from one type to another. So, when a pendulum swings, kinetic energy is converted into potential energy and vice versa.