Derivative of multiplication. Derivative of a function

Solving physical problems or examples in mathematics is completely impossible without knowledge of the derivative and methods for calculating it. Derivative is one of the most important concepts mathematical analysis. We decided to devote today’s article to this fundamental topic. What is a derivative, what is its physical and geometric meaning how to calculate the derivative of a function? All these questions can be combined into one: how to understand the derivative?

Geometric and physical meaning of derivative

Let there be a function f(x) , specified in a certain interval (a, b) . Points x and x0 belong to this interval. When x changes, the function itself changes. Changing the argument - the difference in its values x-x0 . This difference is written as delta x and is called argument increment. A change or increment of a function is the difference between the values of a function at two points. Definition of derivative:

The derivative of a function at a point is the limit of the ratio of the increment of the function at a given point to the increment of the argument when the latter tends to zero.

Otherwise it can be written like this:

What's the point of finding such a limit? And here's what it is:

the derivative of a function at a point is equal to the tangent of the angle between the OX axis and the tangent to the graph of the function at a given point.

Physical meaning derivative: the derivative of the path with respect to time is equal to the speed of rectilinear motion.

Indeed, since school days everyone knows that speed is a particular path x=f(t) and time t . Average speed for a certain period of time:

To find out the speed of movement at a moment in time t0 you need to calculate the limit:

Rule one: set a constant

The constant can be taken out of the derivative sign. Moreover, this must be done. When solving examples in mathematics, take it as a rule - If you can simplify an expression, be sure to simplify it .

Example. Let's calculate the derivative:

Rule two: derivative of the sum of functions

The derivative of the sum of two functions is equal to the sum of the derivatives of these functions. The same is true for the derivative of the difference of functions.

We will not give a proof of this theorem, but rather consider a practical example.

Find the derivative of the function:

Rule three: derivative of the product of functions

The derivative of the product of two differentiable functions is calculated by the formula:

Example: find the derivative of a function:

Solution:

It is important to talk about calculating derivatives of complex functions here. The derivative of a complex function is equal to the product of the derivative of this function with respect to the intermediate argument and the derivative of the intermediate argument with respect to the independent variable.

In the above example we come across the expression:

In this case, the intermediate argument is 8x to the fifth power. In order to calculate the derivative of such an expression, we first calculate the derivative of the external function with respect to the intermediate argument, and then multiply by the derivative of the intermediate argument itself with respect to the independent variable.

Rule four: derivative of the quotient of two functions

Formula for determining the derivative of the quotient of two functions:

We tried to talk about derivatives for dummies from scratch. This topic is not as simple as it seems, so be warned: there are often pitfalls in the examples, so be careful when calculating derivatives.

With any questions on this and other topics, you can contact the student service. For short term We will help you solve the most difficult tests and solve problems, even if you have never done derivative calculations before.

Let the functions u be defined in a certain neighborhood of a point and have derivatives at the point. Then their product has a derivative at the point, which is determined by the formula:
(1) .

Proof

Let us introduce the following notation:
;
.
Here and are functions of the variables and . But for ease of notation, we will omit the designations of their arguments.

Next we notice that
;
.
By condition, the functions and have derivatives at the point, which are the following limits:
;
.
From the existence of derivatives it follows that the functions and are continuous at the point. That's why
;
.

Consider the function y of the variable x, which is the product of the functions and:
.
Let's consider the increment of this function at the point:

.
Now we find the derivative:

.

So,
.
The rule has been proven.

Instead of a variable, you can use any other variable. Let's denote it as x. Then if there are derivatives and , then the derivative of the product of two functions is determined by the formula:
.
Or in a shorter version
(1) .

Consequence

Let them be functions of the independent variable x. Then
;
;
etc...

Let's prove the first formula. First, we apply the product derivative formula (1) for the functions and , and then for the functions and :

.

Other similar formulas are proved in a similar way.

Examples

Example 1

Find the derivative
.

Solution

We apply the rule for differentiating the product of two functions
(1) .
.

From the table of derivatives we find:
;
.
Then
.

Finally we have:
.

Answer

Example 2

Find the derivative of a function from a variable x
.

Solution

We apply the formula for the derivative of the product of two functions:
(1) .
.

We apply the formula for the derivative of the sum and difference of functions:
.
.

We apply the rules for differentiating constants:
;
.
;
.

The operation of finding the derivative is called differentiation.

As a result of solving problems of finding derivatives of the simplest (and not very simple) functions by defining the derivative as the limit of the ratio of the increment to the increment of the argument, a table of derivatives and precisely defined rules of differentiation appeared. The first to work in the field of finding derivatives were Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716).

Therefore, in our time, to find the derivative of any function, you do not need to calculate the above-mentioned limit of the ratio of the increment of the function to the increment of the argument, but you only need to use the table of derivatives and the rules of differentiation. The following algorithm is suitable for finding the derivative.

To find the derivative, you need an expression under the prime sign break down simple functions into components and determine what actions (product, sum, quotient) these functions are related. Next, we find the derivatives of elementary functions in the table of derivatives, and the formulas for the derivatives of the product, sum and quotient - in the rules of differentiation. The derivative table and differentiation rules are given after the first two examples.

Example 1. Find the derivative of a function

Solution. From the rules of differentiation we find out that the derivative of a sum of functions is the sum of derivatives of functions, i.e.

From the table of derivatives we find out that the derivative of “X” is equal to one, and the derivative of sine is equal to cosine. We substitute these values into the sum of derivatives and find the derivative required by the condition of the problem:

Example 2. Find the derivative of a function

Solution. We differentiate as a derivative of a sum in which the second term has a constant factor; it can be taken out of the derivative sign:

If questions still arise about where something comes from, they are usually cleared up after familiarization with the table of derivatives and the simplest rules of differentiation. We are moving on to them right now.

Table of derivatives of simple functions

1. Derivative of a constant (number). Any number (1, 2, 5, 200...) that is in the function expression. Always equal to zero. This is very important to remember, as it is required very often
2. Derivative of the independent variable. Most often "X". Always equal to one. This is also important to remember for a long time
3. Derivative of degree. When solving problems, you need to convert non-square roots into powers.
4. Derivative of a variable to the power -1
5. Derivative square root
6. Derivative of sine
7. Derivative of cosine
8. Derivative of tangent
9. Derivative of cotangent
10. Derivative of arcsine
11. Derivative of arccosine
12. Derivative of arctangent
13. Derivative of arc cotangent
14. Derivative of the natural logarithm
15. Derivative of a logarithmic function
16. Derivative of the exponent
17. Derivative of an exponential function

Rules of differentiation

1. Derivative of a sum or difference
2. Derivative of the product
2a. Derivative of an expression multiplied by a constant factor
3. Derivative of the quotient
4. Derivative of a complex function

Rule 1.If the functions

are differentiable at some point, then the functions are differentiable at the same point

and

those. the derivative of an algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions.

Consequence. If two differentiable functions differ by a constant term, then their derivatives are equal, i.e.

Rule 2.If the functions

are differentiable at some point, then their product is differentiable at the same point

and

those. The derivative of the product of two functions is equal to the sum of the products of each of these functions and the derivative of the other.

Corollary 1. The constant factor can be taken out of the sign of the derivative:

Corollary 2. The derivative of the product of several differentiable functions is equal to the sum of the products of the derivative of each factor and all the others.

For example, for three multipliers:

Rule 3.If the functions

differentiable at some point And , then at this point their quotient is also differentiableu/v , and

those. the derivative of the quotient of two functions is equal to a fraction, the numerator of which is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator.

Where to look for things on other pages

When finding the derivative of a product and a quotient in real problems, it is always necessary to apply several differentiation rules at once, so there are more examples on these derivatives in the article"Derivative of the product and quotient of functions".

Comment. You should not confuse a constant (that is, a number) as a term in a sum and as a constant factor! In the case of a term, its derivative is equal to zero, and in the case of a constant factor, it is taken out of the sign of the derivatives. This typical mistake, which occurs on initial stage studying derivatives, but as they solve several one- and two-part examples, the average student no longer makes this mistake.

And if, when differentiating a product or quotient, you have a term u"v, in which u- a number, for example, 2 or 5, that is, a constant, then the derivative of this number will be equal to zero and, therefore, the entire term will be equal to zero (this case is discussed in example 10).

Another common mistake is mechanically solving the derivative of a complex function as the derivative of a simple function. That's why derivative of a complex function a separate article is devoted. But first we will learn to find derivatives of simple functions.

Along the way, you can’t do without transforming expressions. To do this, you may need to open the manual in new windows. Actions with powers and roots And Operations with fractions .

If you are looking for solutions to derivatives of fractions with powers and roots, that is, when the function looks like , then follow the lesson “Derivative of sums of fractions with powers and roots.”

If you have a task like , then you will take the lesson “Derivatives of simple trigonometric functions”.

Step-by-step examples - how to find the derivative

Example 3. Find the derivative of a function

Solution. We define the parts of the function expression: the entire expression represents a product, and its factors are sums, in the second of which one of the terms contains a constant factor. We apply the product differentiation rule: the derivative of the product of two functions is equal to the sum of the products of each of these functions by the derivative of the other:

Next, we apply the rule of sum differentiation: the derivative of an algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions. In our case, in each sum the second term has a minus sign. In each sum we see both an independent variable, the derivative of which is equal to one, and a constant (number), the derivative of which is equal to zero. So, “X” turns into one, and minus 5 turns into zero. In the second expression, "x" is multiplied by 2, so we multiply two by the same unit as the derivative of "x". We obtain the following values of derivatives:

We substitute the found derivatives into the sum of products and obtain the derivative of the entire function required by the condition of the problem:

Example 4. Find the derivative of a function

Solution. We are required to find the derivative of the quotient. We apply the formula for differentiating the quotient: the derivative of the quotient of two functions is equal to a fraction, the numerator of which is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the former numerator. We get:

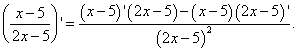
We have already found the derivative of the factors in the numerator in example 2. Let us also not forget that the product, which is the second factor in the numerator in the current example, is taken with a minus sign:

If you are looking for solutions to problems in which you need to find the derivative of a function, where there is a continuous pile of roots and powers, such as, for example, , then welcome to class "Derivative of sums of fractions with powers and roots" .

If you need to learn more about the derivatives of sines, cosines, tangents and others trigonometric functions, that is, when the function looks like , then a lesson for you "Derivatives of simple trigonometric functions" .

Example 5. Find the derivative of a function

Solution. In this function we see a product, one of the factors of which is the square root of the independent variable, the derivative of which we familiarized ourselves with in the table of derivatives. Using the rule for differentiating the product and the tabular value of the derivative of the square root, we obtain:

Example 6. Find the derivative of a function

Solution. In this function we see a quotient whose dividend is the square root of the independent variable. Using the rule of differentiation of quotients, which we repeated and applied in example 4, and the tabulated value of the derivative of the square root, we obtain:

To get rid of a fraction in the numerator, multiply the numerator and denominator by .

WITH editing materials on the topic “derivative”. Basic school level.
Theoretical information for students, teachers and tutors in mathematics. To help conduct classes.

Definition: the derivative of a function at a point is the limit of the ratio of the increment of the function to the increment of the variable, that is

Table of derivatives of basic mathematical functions:

Rules for calculating derivatives

Derivative of the sum any two expressions is equal to the sum of the derivatives of these expressions (the derivative of the sum is equal to the sum of the derivatives)

Derivative of the difference any two expressions is equal to the difference of the derivatives of these terms (the derivative of the difference is equal to the difference of the derivatives).

Derivative of the product two factors is equal to the product of the derivative of the first factor and the second plus the product of the first factor and the derivative of the second (the sum of the derivatives of the factors taken in turn).
Math tutor comment: when I in short phrases I remind the student about the rule for calculating the derivative of a product, I say this: the derivative of the first factor by the second plus exchange strokes!

Derivative of quotient two expressions is equal to the quotient of the difference between the derivatives of the factors taken in turn and the square of the denominator.

Derivative of the product of a number and a function. To find the derivative of the product of a number and a literal expression (function), you need to multiply this number by the derivative of this literal expression.

Derivative of a complex function:

To calculate the derivative of a complex function, you need to find the derivative of the outer function and multiply it by the derivative of the inner function.

Your comments and feedback on the derivatives page:
Alexander S.
I really needed a table. One of the most on the Internet. Thank you very much for the explanations and rules too. At least one more example would be great for them. Thank you very much again.

Kolpakov A.N., mathematics tutor: ok, I’ll try to update the page with examples in the near future.

Virtual mathematical reference book.
Kolpakov Alexander Nikolaevich, mathematics tutor.

If you follow the definition, then the derivative of a function at a point is the limit of the ratio of the increment of the function Δ y to the argument increment Δ x:

Everything seems to be clear. But try using this formula to calculate, say, the derivative of the function f(x) = x 2 + (2x+ 3) · e x sin x. If you do everything by definition, then after a couple of pages of calculations you will simply fall asleep. Therefore, there are simpler and more effective ways.

To begin with, we note that from the entire variety of functions we can distinguish the so-called elementary functions. It's relative simple expressions, the derivatives of which have long been calculated and listed in the table. Such functions are quite easy to remember - along with their derivatives.

Derivatives of elementary functions

Elementary functions are all those listed below. The derivatives of these functions must be known by heart. Moreover, it is not at all difficult to memorize them - that’s why they are elementary.

So, derivatives of elementary functions:

Name	Function	Derivative
Constant	f(x) = C, C ∈ R	0 (yes, zero!)
Power with rational exponent	f(x) = x n	n · x n − 1
Sinus	f(x) = sin x	cos x
Cosine	f(x) = cos x	−sin x(minus sine)
Tangent	f(x) = tg x	1/cos 2 x
Cotangent	f(x) = ctg x	− 1/sin 2 x
Natural logarithm	f(x) = log x	1/x
Arbitrary logarithm	f(x) = log a x	1/(x ln a)
Exponential function	f(x) = e x	e x(nothing has changed)

If an elementary function is multiplied by an arbitrary constant, then the derivative of the new function is also easily calculated:

(C · f)’ = C · f ’.

In general, constants can be taken out of the sign of the derivative. For example:

(2x 3)’ = 2 · ( x 3)’ = 2 3 x 2 = 6x 2 .

Obviously, elementary functions can be added to each other, multiplied, divided - and much more. This is how new functions will appear, no longer particularly elementary, but also differentiated according to certain rules. These rules are discussed below.

Derivative of sum and difference

Let the functions be given f(x) And g(x), the derivatives of which are known to us. For example, you can take the elementary functions discussed above. Then you can find the derivative of the sum and difference of these functions:

(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’

So, the derivative of the sum (difference) of two functions is equal to the sum (difference) of the derivatives. There may be more terms. For example, ( f + g + h)’ = f ’ + g ’ + h ’.

Strictly speaking, there is no concept of “subtraction” in algebra. There is a concept of “negative element”. Therefore the difference f − g can be rewritten as a sum f+ (−1) g, and then only one formula remains - the derivative of the sum.

f(x) = x 2 + sin x; g(x) = x 4 + 2x 2 − 3.

Function f(x) is the sum of two elementary functions, therefore:

f ’(x) = (x 2 + sin x)’ = (x 2)’ + (sin x)’ = 2x+ cos x;

We reason similarly for the function g(x). Only there are already three terms (from the point of view of algebra):

g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).

Answer:
f ’(x) = 2x+ cos x;
g ’(x) = 4x · ( x 2 + 1).

Derivative of the product

Mathematics is a logical science, so many people believe that if the derivative of a sum is equal to the sum of derivatives, then the derivative of the product strike">equal to the product of derivatives. But screw you! The derivative of a product is calculated using a completely different formula. Namely:

(f · g) ’ = f ’ · g + f · g ’

The formula is simple, but it is often forgotten. And not only schoolchildren, but also students. The result is incorrectly solved problems.

Task. Find derivatives of functions: f(x) = x 3 cos x; g(x) = (x 2 + 7x− 7) · e x .

Function f(x) is the product of two elementary functions, so everything is simple:

f ’(x) = (x 3 cos x)’ = (x 3)’ cos x + x 3 (cos x)’ = 3x 2 cos x + x 3 (−sin x) = x 2 (3cos x − x sin x)

Function g(x) the first factor is a little more complicated, but general scheme this doesn't change. Obviously, the first factor of the function g(x) is a polynomial and its derivative is the derivative of the sum. We have:

g ’(x) = ((x 2 + 7x− 7) · e x)’ = (x 2 + 7x− 7)’ · e x + (x 2 + 7x− 7) ( e x)’ = (2x+ 7) · e x + (x 2 + 7x− 7) · e x = e x· (2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · e x = x(x+ 9) · e x .

Answer:
f ’(x) = x 2 (3cos x − x sin x);
g ’(x) = x(x+ 9) · e x .

Please note that in the last step the derivative is factorized. Formally, this does not need to be done, but most derivatives are not calculated on their own, but to examine the function. This means that further the derivative will be equated to zero, its signs will be determined, and so on. For such a case, it is better to have an expression factorized.

If there are two functions f(x) And g(x), and g(x) ≠ 0 on the set we are interested in, we can define a new function h(x) = f(x)/g(x). For such a function you can also find the derivative:

Not weak, right? Where did the minus come from? Why g 2? And so! This is one of the most complex formulas - you can’t figure it out without a bottle. Therefore, it is better to study it with specific examples.

Task. Find derivatives of functions:

The numerator and denominator of each fraction contain elementary functions, so all we need is the formula for the derivative of the quotient:

According to tradition, let's factorize the numerator - this will greatly simplify the answer:

A complex function is not necessarily a half-kilometer-long formula. For example, it is enough to take the function f(x) = sin x and replace the variable x, say, on x 2 + ln x. It will work out f(x) = sin ( x 2 + ln x) - this is it complex function. It also has a derivative, but it will not be possible to find it using the rules discussed above.

What should I do? In such cases, replacing a variable and formula for the derivative of a complex function helps:

f ’(x) = f ’(t) · t', If x is replaced by t(x).

As a rule, the situation with understanding this formula is even more sad than with the derivative of the quotient. Therefore, it is also better to explain it using specific examples, with a detailed description of each step.

Task. Find derivatives of functions: f(x) = e 2x + 3 ; g(x) = sin ( x 2 + ln x)

Note that if in the function f(x) instead of expression 2 x+ 3 will be easy x, then it will work out elementary function f(x) = e x. Therefore, we make a replacement: let 2 x + 3 = t, f(x) = f(t) = e t. We look for the derivative of a complex function using the formula:

f ’(x) = f ’(t) · t ’ = (e t)’ · t ’ = e t · t ’

And now - attention! We perform the reverse replacement: t = 2x+ 3. We get:

f ’(x) = e t · t ’ = e 2x+ 3 (2 x + 3)’ = e 2x+ 3 2 = 2 e 2x + 3

Now let's look at the function g(x). Obviously it needs to be replaced x 2 + ln x = t. We have:

g ’(x) = g ’(t) · t’ = (sin t)’ · t’ = cos t · t ’

Reverse replacement: t = x 2 + ln x. Then:

g ’(x) = cos ( x 2 + ln x) · ( x 2 + ln x)’ = cos ( x 2 + ln x) · (2 x + 1/x).

That's it! As can be seen from the last expression, the whole problem has been reduced to calculating the derivative sum.

Answer:
f ’(x) = 2 · e 2x + 3 ;
g ’(x) = (2x + 1/x) cos ( x 2 + ln x).

Very often in my lessons, instead of the term “derivative,” I use the word “prime.” For example, the stroke of the sum is equal to the sum of the strokes. Is that clearer? Well, that's good.

Thus, calculating the derivative comes down to getting rid of these same strokes according to the rules discussed above. As a final example, let's return to the derivative power with a rational exponent:

(x n)’ = n · x n − 1

Few people know that in the role n may well be a fractional number. For example, the root is x 0.5. What if there is something fancy under the root? Again, the result will be a complex function - they like to give such constructions to tests and exams.