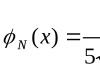Centripetal acceleration- component of the acceleration of a point, characterizing the speed of change in the direction of the velocity vector for a trajectory with curvature (the second component, tangential acceleration, characterizes the change in the velocity module). Directed towards the center of curvature of the trajectory, which is where the term comes from. The value is equal to the square of the speed divided by the radius of curvature. The term "centripetal acceleration" is equivalent to the term " normal acceleration" That component of the sum of forces that causes this acceleration is called centripetal force.

Most simple example centripetal acceleration is the acceleration vector at uniform motion circumferentially (directed towards the center of the circle).

Rapid acceleration in projection onto a plane perpendicular to the axis, it appears as centripetal.

Encyclopedic YouTube

• 1 / 5

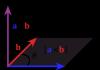
  A n = v 2 R (\displaystyle a_(n)=(\frac (v^(2))(R))\ ) a n = ω 2 R , (\displaystyle a_(n)=\omega ^(2)R\ ,)

  Where a n (\displaystyle a_(n)\ )- normal (centripetal) acceleration, v (\displaystyle v\ )- (instantaneous) linear speed of movement along the trajectory, ω (\displaystyle \omega \ )- (instantaneous) angular velocity of this movement relative to the center of curvature of the trajectory, R (\displaystyle R\ )- radius of curvature of the trajectory at a given point. (The connection between the first formula and the second is obvious, given v = ω R (\displaystyle v=\omega R\ )).

  The expressions above include absolute values. They can be easily written in vector form by multiplying by e R (\displaystyle \mathbf (e)_(R))- unit vector from the center of curvature of the trajectory to its given point:

  a n = v 2 R e R = v 2 R 2 R (\displaystyle \mathbf (a) _(n)=(\frac (v^(2))(R))\mathbf (e) _(R)= (\frac (v^(2))(R^(2)))\mathbf (R) ) a n = ω 2 R .

  (\displaystyle \mathbf (a) _(n)=\omega ^(2)\mathbf (R) .) These formulas are equally applicable to the case of motion with a constant (in absolute value) speed and to an arbitrary case. However, in the second, one must keep in mind that centripetal acceleration is not the full acceleration vector, but only its component perpendicular to the trajectory (or, what is the same, perpendicular to the instantaneous velocity vector); the full acceleration vector then also includes a tangential component () tangential acceleration a τ = d v / d t (\displaystyle a_(\tau )=dv/dt\ )

  , in direction coinciding with the tangent to the trajectory (or, what is the same, with the instantaneous speed).

  Motivation and conclusion The fact that the decomposition of the acceleration vector into components - one along the tangent to the vector trajectory (tangential acceleration) and the other orthogonal to it (normal acceleration) - can be convenient and useful is quite obvious in itself. When moving with a constant modulus speed, the tangential component becomes equal to zero, that is, in this important particular case it remains only

  normal component. In addition, as can be seen below, each of these components has clearly defined properties and structure, and normal acceleration contains quite important and non-trivial geometric content in the structure of its formula. Not to mention the important special case of circular motion.

  Formal conclusion The decomposition of acceleration into tangential and normal components (the second of which is centripetal or normal acceleration) can be found by differentiating with respect to time the velocity vector, presented in the form v = v e τ (\displaystyle \mathbf (v) =v\,\mathbf (e) _(\tau )) through the unit tangent vector:

  a = d v d t = d (v e τ) d t = d v d t e τ + v d e τ d t = d v d t e τ + v d e τ d l d l d t = d v d t e τ + v 2 R e n , (\displaystyle \mathbf (a) =(\frac (d\mathbf ( v) )(dt))=(\frac (d(v\mathbf (e) _(\tau )))(dt))=(\frac (\mathrm (d) v)(\mathrm (d) t ))\mathbf (e) _(\tau )+v(\frac (d\mathbf (e) _(\tau ))(dt))=(\frac (\mathrm (d) v)(\mathrm ( d) t))\mathbf (e) _(\tau )+v(\frac (d\mathbf (e) _(\tau ))(dl))(\frac (dl)(dt))=(\ frac (\mathrm (d) v)(\mathrm (d) t))\mathbf (e) _(\tau )+(\frac (v^(2))(R))\mathbf (e) _( n)\ ,)

  Here we use the notation for the unit vector normal to the trajectory and l (\displaystyle l\ )- for the current trajectory length ( l = l (t) (\displaystyle l=l(t)\ )); the last transition also uses the obvious

  d l / d t = v (\displaystyle dl/dt=v\ )

  and, from geometric considerations,

  d e τ d l = e n R . (\displaystyle (\frac (d\mathbf (e) _(\tau ))(dl))=(\frac (\mathbf (e) _(n))(R)).)

  v 2 R e n (\displaystyle (\frac (v^(2))(R))\mathbf (e) _(n)\ ) Normal (centripetal) acceleration. Moreover, its meaning, the meaning of the objects included in it, as well as proof of the fact that it is indeed orthogonal to the tangent vector (that is, that e n (\displaystyle \mathbf (e)_(n)\ ) - really a normal vector) - will follow from geometric considerations (however, the fact that the derivative of any vector of constant length with respect to time is perpendicular to this vector itself is a fairly simple fact; in this case we apply this statement to

  d e τ d t (\displaystyle (\frac (d\mathbf (e) _(\tau ))(dt)))

  Notes It is easy to notice that the absolute value of the tangential acceleration depends only on the directional acceleration, coinciding with its absolute value, in contrast to the absolute value normal acceleration

  , which does not depend on ground acceleration, but depends on ground speed. The methods presented here, or variations thereof, can be used to introduce concepts such as the curvature of a curve and the radius of curvature of a curve (since in the case where the curve is a circle, R (\displaystyle R) coincides with the radius of such a circle; it is not too difficult to show that the circle is in the plane e τ , e n (\displaystyle \mathbf (e) _(\tau ),\,e_(n)) with center in direction e n (\displaystyle e_(n)\ ) The methods presented here, or variations thereof, can be used to introduce concepts such as the curvature of a curve and the radius of curvature of a curve (since in the case where the curve is a circle, from it - will coincide with the given curve - trajectory - up to the second order of smallness in the distance to the given point).

  Story

  First correct formulas for centripetal acceleration (or centrifugal force) was apparently obtained by Huygens. Almost from this time on, consideration of centripetal acceleration has become part of the usual technique for solving mechanical problems, etc.

  Somewhat later, these formulas played a significant role in the discovery of the law of universal gravitation (the formula of centripetal acceleration was used to obtain the law of dependence gravitational force from the distance to the source of gravity, based on Kepler’s third law derived from observations).

  TO 19th century consideration of centripetal acceleration is already becoming completely routine both for pure science and for engineering applications.

  Allows us to exist on this planet. How can we understand what centripetal acceleration is? Definition of this physical quantity presented below.

  Observations

  The simplest example of the acceleration of a body moving in a circle can be observed by rotating a stone on a rope. You pull the rope, and the rope pulls the stone towards the center. At each moment of time, the rope imparts a certain amount of movement to the stone, and each time in a new direction. You can imagine the movement of the rope as a series of weak jerks. A jerk - and the rope changes its direction, another jerk - another change, and so on in a circle. If you suddenly release the rope, the jerking will stop, and with it the change in direction of speed will stop. The stone will move in the direction tangent to the circle. The question arises: “With what acceleration will the body move at this instant?”

  Formula for centripetal acceleration

  First of all, it is worth noting that the movement of a body in a circle is complex. The stone participates in two types of motion simultaneously: under the influence of force it moves towards the center of rotation, and at the same time along a tangent to the circle, moving away from this center. According to Newton's Second Law, the force holding a stone on a rope is directed toward the center of rotation along the rope. The acceleration vector will also be directed there.

  Let us assume that after some time t, our stone, moving uniformly with speed V, gets from point A to point B. Let us assume that at the moment of time when the body crossed point B, the centripetal force ceased to act on it. Then, in a period of time, it would get to point K. It lies on the tangent. If at the same moment of time only centripetal forces acted on the body, then during time t, moving with the same acceleration, it would end up at point O, which is located on a straight line representing the diameter of a circle. Both segments are vectors and obey the rule vector addition. As a result of summing these two movements over a period of time t, we obtain the resulting movement along the arc AB.

  

  If the time interval t is taken to be negligibly small, then the arc AB will differ little from the chord AB. Thus, it is possible to replace movement along an arc with movement along a chord. In this case, the movement of the stone along the chord will obey the laws of rectilinear motion, that is, the distance AB traveled will be equal to the product of the speed of the stone and the time of its movement. AB = V x t.

  Let us denote the desired centripetal acceleration by the letter a. Then the path traveled only under the influence of centripetal acceleration can be calculated using the formula for uniformly accelerated motion:

  Distance AB is equal to the product of speed and time, that is, AB = V x t,

  AO - calculated earlier using the formula of uniformly accelerated motion for moving in a straight line: AO = at 2 / 2.

  Substituting this data into the formula and transforming it, we get a simple and elegant formula for centripetal acceleration:

  In words, this can be expressed as follows: the centripetal acceleration of a body moving in a circle is equal to the quotient of linear velocity squared by the radius of the circle along which the body rotates. The centripetal force in this case will look like the picture below.

  

  Angular velocity

  Angular velocity is equal to the linear velocity divided by the radius of the circle. The converse statement is also true: V = ωR, where ω is the angular velocity

  If we substitute this value into the formula, we can obtain an expression for the centrifugal acceleration for the angular velocity. It will look like this:

  Acceleration without changing speed

  And yet, why does a body with acceleration directed towards the center not move faster and move closer to the center of rotation? The answer lies in the very formulation of acceleration. The facts show that circular motion is real, but to maintain it requires acceleration directed towards the center. Under the influence of the force caused by this acceleration, a change in the amount of motion occurs, as a result of which the trajectory of motion is constantly curved, all the time changing the direction of the velocity vector, but without changing its absolute value. Moving in a circle, our long-suffering stone rushes inward, otherwise it would continue to move tangentially. Every moment of time, going tangentially, the stone is attracted to the center, but does not fall into it. Another example of centripetal acceleration would be a water skier making small circles on the water. The athlete's figure is tilted; he seems to fall, continuing to move and leaning forward.

  

  Thus, we can conclude that acceleration does not increase the speed of the body, since the velocity and acceleration vectors are perpendicular to each other. Added to the velocity vector, acceleration only changes the direction of movement and keeps the body in orbit.

  Exceeding the safety factor

  In the previous experiment we were dealing with a perfect rope that did not break. But let’s say our rope is the most ordinary, and you can even calculate the force after which it will simply break. In order to calculate this force, it is enough to compare the strength of the rope with the load it experiences during the rotation of the stone. By rotating the stone at a faster speed, you tell it large quantity movement, and therefore greater acceleration.

  

  With a jute rope diameter of about 20 mm, its tensile strength is about 26 kN. It is noteworthy that the length of the rope does not appear anywhere. By rotating a 1 kg load on a rope with a radius of 1 m, we can calculate that the linear speed required to break it is 26 x 10 3 = 1 kg x V 2 / 1 m. Thus, the speed that is dangerous to exceed will be equal to √ 26 x 10 3 = 161 m/s.

  Gravity

  When considering the experiment, we neglected the effect of gravity, since at such high speeds its influence is negligible. But you can notice that when unwinding a long rope, the body describes a more complex trajectory and gradually approaches the ground.

  Celestial bodies

  If we transfer the laws of circular motion into space and apply them to the movement of celestial bodies, we can rediscover several long-familiar formulas. For example, the force with which a body is attracted to the Earth is known by the formula:

  In our case, the factor g is the same centripetal acceleration that was derived from the previous formula. Only in this case will the role of the stone be played by heavenly body, attracted to the Earth, and the role of the rope is force gravity. The g factor will be expressed in terms of the radius of our planet and its rotation speed.

  

  Results

  The essence of centripetal acceleration is the hard and thankless work of keeping a moving body in orbit. A paradoxical case is observed when, with constant acceleration, a body does not change the value of its speed. To the untrained mind, such a statement is quite paradoxical. Nevertheless, both when calculating the motion of an electron around a nucleus, and when calculating the speed of rotation of a star around a black hole, centripetal acceleration plays an important role.

  Two rays emanating from it form an angle. Its value can be defined in both radians and degrees. Now, at some distance from the center point, let’s mentally draw a circle. The measure of angle, expressed in radians, is then the mathematical ratio of the length of the arc L, separated by two rays, to the value of the distance between the center point and the line of the circle (R), that is:

  If we now imagine the described system as material, then we can apply to it not only the concept of angle and radius, but also centripetal acceleration, rotation, etc. Most of them describe the behavior of a point located on a rotating circle. By the way, a solid disk can also be represented by a set of circles, the difference of which is only in the distance from the center.

  One of the characteristics of such a rotating system is its orbital period. It indicates the time value during which a point on an arbitrary circle will return to its initial position or, which is also true, turn 360 degrees. At a constant rotation speed, the correspondence T = (2*3.1416) / Ug is satisfied (hereinafter Ug is the angle).

  The rotation speed indicates the amount full revolutions, executed in 1 second. At a constant speed we get v = 1 / T.

  Depends on time and the so-called rotation angle. That is, if we take an arbitrary point A on the circle as the origin, then when the system rotates, this point will move to A1 in time t, forming an angle between the radii A-center and A1-center. Knowing the time and angle, you can calculate the angular velocity.

  And since there is a circle, movement and speed, it means that centripetal acceleration is also present. It represents one of the components that describe movement in the case of curvilinear movement. The terms "normal" and "centripetal acceleration" are identical. The difference is that the second is used to describe movement in a circle when the acceleration vector is directed towards the center of the system. Therefore, it is always necessary to know exactly how the body (point) moves and its centripetal acceleration. Its definition is as follows: it is the rate of change of speed, the vector of which is directed perpendicular to the direction of the vector and changes the direction of the latter. The encyclopedia states that Huygens studied this issue. The formula for centripetal acceleration proposed by him looks like:

  Acs = (v*v) / r,

  where r is the radius of curvature of the traveled path; v - movement speed.

  The formula used to calculate centripetal acceleration still causes heated debate among enthusiasts. For example, an interesting theory was recently voiced.

  Huygens, considering the system, proceeded from the fact that the body moves in a circle of radius R with a speed v measured in starting point A. Since the vector of inertia is directed along, the trajectory is obtained in the form of a straight line AB. However, the centripetal force holds the body on the circle at point C. If we mark the center as O and draw lines AB, BO (the sum of BS and CO), as well as AO, we get a triangle. According to the Pythagorean law:

  BS=(a*(t*t)) / 2, where a is acceleration; t - time (a*t*t is the speed).

  If we now use the Pythagorean formula, then:

  R2+t2+v2 = R2+(a*t2*2*R) / 2+ (a*t2/2)2, where R is the radius, and the alphanumeric spelling without the multiplication sign is the degree.

  Huygens admitted that since the time t is small, it can be ignored in the calculations. Having transformed the previous formula, she came to the well-known Acs = (v*v) / r.

  However, since time is taken squared, a progression arises: the larger t, the higher the error. For example, for 0.9 almost the total value of 20% is unaccounted for.

  The concept of centripetal acceleration is important for modern science, but, obviously, it’s too early to put an end to this issue.

  Let a material point move uniformly around a circle. Then the modulus of its velocity does not change ($v=const$). But this does not mean that acceleration material point equals zero. The velocity vector is directed tangentially to the trajectory of the point. When moving around a circle, the speed changes its direction constantly. This means that the point is moving with acceleration.

  Let's consider points A and B belonging to the trajectory of the body in question. The velocity change vector for these points is equal to:

  \[\Delta \overline(v)=(\overline(v))"-\overline(v)\left(1\right).\]

  If the time of movement between points A and B is short, then the arc AB differs little from the chord AB. Triangles AOB and BMN are similar, therefore:

  \[\frac(\Delta v)(v)=\frac(\Delta l)(r)=\alpha \left(2\right).\]

  We find the average acceleration module as:

  \[\left\langle a\right\rangle =\frac(\Delta v)(\Delta t)=\frac(v\Delta l)(r\Delta t)\left(3\right).\]

  The magnitude of the instantaneous acceleration can be obtained by passing to the limit at $\Delta t\to 0\ $ from $\left\langle a\right\rangle $:

  The average acceleration vector makes an angle equal to the velocity vector:

  \[\beta =\frac(\pi +\alpha )(2)\left(5\right).\]

  At $\Delta t\to 0\ $ angle $\alpha \to 0.$ It turns out that the instantaneous acceleration vector makes an angle $\frac(\pi )(2)$ with the velocity vector.

  We found that a material point moving uniformly around a circle has an acceleration directed to the center of the motion trajectory (perpendicular to the velocity vector), its modulus equal to speed squared divided by the radius of the circle. This acceleration is called centripetal or normal, it is usually denoted by $(\overline(a))_n$.

  where $\omega $ is the angular velocity of motion of a material point ($v=\omega \cdot r$).

  Definition of centripetal acceleration

  Definition

  So, centripetal acceleration(in the general case) is a component of the total acceleration of a material point, which characterizes how quickly the direction of the velocity vector changes during curvilinear movement. Another component of total acceleration is tangential acceleration, which is responsible for the change in velocity.

  Centripetal acceleration is equal to:

  \[(\overline(a))_n=\frac(v^2)(r^2)\overline(r\ )\left(7\right),\]

  where $e_r=\frac(\overline(r\ ))(r)$ is the unit vector directed from the center of curvature of the trajectory to the point under consideration.

  For the first time, the correct formulas for centripetal acceleration were obtained by H. Huygens.

  The International System of Units unit of centripetal acceleration is the meter divided by the squared second:

  \[\left=\frac(m)(s^2).\]

  Examples of problems with solutions

  Example 1

  Exercise. The disk rotates around fixed axis. The law of changing the angle of rotation of the radius of the disk sets the equation: $\varphi =5t^2+7\ (rad)$. What is the centripetal acceleration of point A of the disk, which is located at a distance of $r=$0.5 m from the axis of rotation at the end of the fourth second from the start of rotation?

  Solution. Let's make a drawing.

  

  The modulus of centripetal acceleration is equal to: \

  We find the angular velocity of rotation of the point as:

  \[\omega =\frac(d\varphi )(dt)\ (1.2)\]

  equation for changing the angle of rotation depending on time:

  \[\omega =\frac(d\left(5t^2+7\right))(dt)=10t\ \left(1.3\right).\]

  At the end of the fourth second, the angular velocity is:

  \[\omega \left(t=4\right)=10\cdot 4=40\ \left(\frac(rad)(s)\right).\]

  Using expression (1.1) we find the value of centripetal acceleration:

  Answer.$a_n=800\frac(m)(s^2)$.

  Example 2

  Exercise. The motion of a material point is specified using the equation: $\overline(r)\left(t\right)=0.5\ (\overline(i)(\cos \left(\omega t\right)+\overline(j) (\sin (\omega t)\ )\ ))$, where $\omega =2\ \frac(rad)(s)$. What is the magnitude of the normal acceleration of a point?

  Solution. As a basis for solving the problem, we will take the definition of centripetal acceleration in the form:

  From the conditions of the problem it is clear that the trajectory of the point is a circle. In parametric form, the equation is: $\overline(r)\left(t\right)=0.5\ (\overline(i)(\cos \left(\omega t\right)+\overline(j)(\sin (\omega t)\ )\ ))$, where $\omega =2\ \frac(rad)(s)$ can be represented as:

  \[\left\( \begin(array)(c) x=0.5(\cos \left(2t\right);;\ ) \\ y=0.5(\sin \left(2t\right) .\ ) \end(array) \right.\]

  The trajectory radius can be found as:

  The velocity components are equal:

  \ \

  Let's get the speed module:

  Substitute the speed value and the radius of the circle into expression (2.2), we have:

  Answer.$a_n=2\frac(m)(s^2)$.