Ministry of Education and Science of the Russian Federation
Saratov State Technical University
Balakovo Institute of Engineering, Technology and Management
Harmonic linearization method
Guidelines for laboratory work in the course "Theory" automatic control» for students of specialty 210100
Approved
editorial and publishing council
Balakovo Institute of Technology,
technology and management
Balakovo 2004
Purpose of the work: Study of nonlinear systems using the method of harmonic linearization (harmonic balance), determination of harmonic linearization coefficients for various nonlinear links. Gaining skills in finding the parameters of symmetrical oscillations of constant amplitude and frequency (self-oscillations), using algebraic, frequency methods, and also using the Mikhailov criterion.
BASIC INFORMATION
The harmonic linearization method refers to approximate methods for studying nonlinear systems. It allows one to quite simply and with acceptable accuracy evaluate the stability of nonlinear systems and determine the frequency and amplitude of oscillations established in the system.
It is assumed that the nonlinear ACS under study can be represented in the following form
and the nonlinear part must have one nonlinearity
. (1)
This nonlinearity can be either continuous or relay, single-valued or hysteretic.
Any function or signal can be expanded into a series according to a system of linearly independent, in a particular case, orthonormal functions. The Fourier series can be used as such an orthogonal series.
Let us expand the output signal of the nonlinear part of the system into a Fourier series
, (2)
here are the Fourier coefficients,
,
,
. (3)
Thus, the signal according to (2) can be represented in the form infinite sum harmonics with increasing frequencies 
etc. This signal is supplied to the input of the linear part of the nonlinear system.
Let us denote the transfer function of the linear part
,
(4)
and the degree of the numerator polynomial must be less than the degree of the denominator polynomial. In this case, the frequency response of the linear part has the form
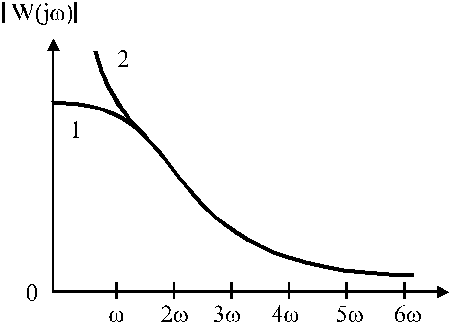
where 1 - has no poles, 2 - has a pole or poles.
For the frequency response it is fair to write
Thus, the linear part of a nonlinear system is a high-pass filter. In this case, the linear part will transmit only low frequencies without attenuation, while high frequencies will be significantly attenuated as the frequency increases.
In the harmonic linearization method, the assumption is made that the linear part of the system will pass only the DC component of the signal and the first harmonic. Then the signal at the output of the linear part will have the form
This signal passes through the entire closed circuit of the system Fig. 1 and at the output of the nonlinear element without taking into account higher harmonics, according to (2) we have
.
(7)
When studying nonlinear systems using the harmonic linearization method, cases of symmetrical and asymmetrical oscillations are possible. Let us consider the case of symmetric oscillations. Here and.
Let us introduce the following notation
,
.
Substituting them into (7), we get . (8)
Considering that
,
, Where ,
. (9)
According to (3) and (8) when
,
. (10)
Expression (9) is the harmonic linearization of the nonlinearity establishes a linear relationship between the input variable and the output variable at . The quantities are called harmonic linearization coefficients.
It should be noted that equation (9) is linear for specific quantities and (the amplitude and frequency of harmonic oscillations in the system). But in general, it retains nonlinear properties, since the coefficients are different for different and . This feature allows us to study the properties of nonlinear systems using the harmonic linearization method [Popov E.P.].
In the case of asymmetric oscillations, harmonic linearization of the nonlinearity leads to the linear equation
,
,
. (12)
Just like equation (9), linearized equation (11) preserves the properties of a nonlinear element, since the harmonic linearization coefficients , , as well as the constant component depend on both the displacement and the amplitude of harmonic oscillations.
Equations (9) and (11) allow us to obtain the transfer functions of harmonically linearized nonlinear elements. So for symmetrical vibrations
Harmonic linearization of nonlinear elements. This method is used to study nonlinear systems with a linear part above the third order. In most systems, the transient process is a damped oscillation, therefore, at the input of the nonlinear element, the main feedback (GOS) is transmitted periodic signal with slowly varying amplitude and in the presence of an input signal along with a constant component.
We will assume that at the input of the nonlinear element for a certain small initial period of time the amplitude and frequency do not change or they correspond to the amplitude and frequency of self-oscillations of the system. At the output of the NE we obtain a periodic function that can be expanded into a Fourier series. When studying nonlinear systems, most often only the first harmonic component is used, because In most cases, the linear part of the system is a low-pass filter. But in order to check this and the applicability of this research method, it is necessary to determine the frequency of self-oscillations in the system, from which we can subsequently determine the ability of the linear part to filter out higher harmonics. For this purpose, the frequency response of the linear part (LP) is built.
Let the LF system be a low-pass filter, and we will assume that the oscillations at the input of the nonlinear NE element are sinusoidal, then the output signal of the NE is:
Where A to And In to– Fourier expansion coefficients of the nonlinear function:
If the nonlinear characteristic is symmetrical and neutral, then the expansion coefficient of the Fourier series In to=0 and there are no even harmonics in the expansion:
Using these relations, we express the value of sine and cosine in terms of the input signal
Let us substitute these relations into the equation for the NE output and take into account only the first harmonic.
Let's write this equation in operator form:
Coefficient A 0 – amplitude of self-oscillations; q is the harmonic linearization coefficient for the sinusoidal component, it depends on the amplitude of the signal at the NE input; b 1 – coefficient of harmonic linearization for the cosine component; ω 0 – amplitude of self-oscillations.
In the absence of a constant component at the input of the NE, we obtain an equation for describing the behavior of the NE:
This is the equation of harmonic linearization of NE.
A harmonically linearized NE can be represented as:
In this case, we can derive the transfer function for the NE:
in the absence of a constant component at the input.
Coefficient A 0 – amplitude of self-oscillations;
q is the coefficient of harmonic linearization for the sinusoidal component, it depends on the amplitude of the signal at the input of the NE;
b 1 – harmonic linearization coefficient for the cosine component;
ω 0 – amplitude of self-oscillations.
The linear part of the system is affected by the output signal from the NE, which contains the entire frequency spectrum of the Fourier expansion. Due to the principle of superposition, we can assume that each harmonic acts on the linear part independently of the other. Therefore, periodic oscillations can be established at the output of the system, which will contain the entire spectrum of frequencies corresponding to the NE signal, but the amplitude of each harmonic will be determined by the conversion coefficient of the right side of the considered harmonic ().
By substituting the frequency response of the linear part, you can establish the ratio of the change in amplitudes for each harmonic and check whether the linear part is a low-pass filter (whether higher harmonics can be discarded).
If the frequency of self-oscillations is established and the harmonic linearization coefficients of the NE are known, taking into account only the first harmonic, then the frequency (frequency of the first harmonic). If so, higher harmonics can be discarded and this method is suitable. Those. we can limit ourselves to calculating only one harmonic at the NE output. Then for a unique odd characteristic the NE will have:
For hysteresis odd characteristic:
In the first case, the NE is equivalent to an inertia-free link with some features - the proportionality coefficient depends on the amplitude or frequency of the signal at the NE input.
In the case of hysteretic nonlinearity, the link is equivalent to the forcing link. The peculiarity of this linearization method allows the use of frequency methods of linear theory to analyze a nonlinear system.
Purpose of the harmonic linearization method.
The idea of the harmonic linearization method was proposed in 1934. N. M. Krylov and N. N. Bogolyubov. In relation to automatic control systems, this method was developed by L. S. Goldfarb and E. P. Popov. Other names for this method and its modifications are the harmonic balance method, the method of describing functions, and the method of equivalent linearization.
The harmonic linearization method is a method for studying self-oscillations. It allows you to determine the conditions of existence and parameters of possible self-oscillations in nonlinear systems.
Knowledge of the parameters of self-oscillations allows us to present a picture of possible processes in the system and, in particular, determine the conditions of stability. Suppose, for example, that as a result of studying self-oscillations in some nonlinear system, we obtained the dependence of the amplitude of these self-oscillations A from transmission coefficient k linear part of the system shown in Fig. 12.1, and we know that self-oscillations are stable.
From the graph it follows that when great importance transmission coefficient k, When k > k kr, there are self-oscillations in the system. Their amplitude decreases to zero as the transmission coefficient decreases k to k cr. In Fig. 12.1, the arrows conventionally show the nature of transient processes when different meanings k: at k > k kr the transient process caused by the initial deviation contracts to self-oscillations. From the figure it is clear that when k< k cr, the system turns out to be stable. Thus, k kr is the critical value of the transmission coefficient according to the stability condition. Exceeding it leads to the fact that the initial mode of the system becomes unstable and self-oscillations arise in it. Consequently, knowledge of the conditions for the existence of self-oscillations in the system allows us to determine the conditions of stability.
The idea of harmonic linearization.
Let's consider a nonlinear system, the diagram of which is shown in Fig. 12.2, and . The system consists of a linear part with a transfer function W l ( s) and nonlinear link NL with a specific characteristic . A link with a coefficient of - 1 shows that the feedback in the system is negative. We believe that there are self-oscillations in the system, the amplitude and frequency of which we want to find. In the considered mode, the input quantity X nonlinear link and output Y are periodic functions time.
The harmonic linearization method is based on the assumption that the oscillations at the input of the nonlinear link are sinusoidal, i.e. e. that
, (12.1)
WhereA– amplitude and is the frequency of these self-oscillations, and is a possible constant component in the general case when the self-oscillations are asymmetrical.
In reality, self-oscillations in nonlinear systems are always nonsinusoidal due to the distortion of their shape by the nonlinear element. Therefore, the specified initial assumption means that the harmonic linearization method is fundamentally close and the scope of its application is limited to cases where self-oscillations at the input of a nonlinear link are quite close to sinusoidal. In order for this to take place, the linear part of the system must not allow higher harmonics of self-oscillations to pass through, i.e., be low pass filter. The latter is illustrated in Fig. 12.2, b . If, for example, the frequency of self-oscillations is equal to , then the linear part shown in Fig. 12.2, b The frequency response will play the role of a low-pass filter for these oscillations, since the second harmonic, whose frequency is equal to 2, will practically not pass to the input of the nonlinear link. Therefore, in this case the harmonic linearization method is applicable.
If the frequency of self-oscillations is equal to , the linear part will freely pass the second, third and other harmonics of self-oscillations. In this case, it cannot be said that the oscillations at the input of the nonlinear link will be quite close to sinusoidal, i.e. the prerequisite necessary for applying the harmonic linearization method is not met.
In order to determine whether the linear part of the system is a low-pass filter and thereby determine the applicability of the harmonic linearization method, it is necessary to know the frequency of self-oscillations. However, it can only be known by using this method. Thus, The applicability of the harmonic linearization method must be determined at the end of the study as a test.
Let us note that if, as a result of this test, the hypothesis that the linear part of the system plays the role of a low-pass filter is not confirmed, this does not mean that the results obtained are incorrect, although, of course, it casts doubt on them and requires additional verification in some way. another method.
So, assuming that the linear part of the system is a low-pass filter, we assume that the self-oscillations at the input of the nonlinear link are sinusoidal, that is, they have the form (12.1). The oscillations at the output of this link will no longer be sinusoidal due to their distortion by nonlinearity. As an example in Fig. 12.3, a curve is plotted at the output of the nonlinear link for a certain amplitude of the input purely sinusoidal signal according to the link characteristic given there.
Fig. 12.3. Passage of a harmonic oscillation through a nonlinear link.
However, since we believe that the linear part of the system passes only the fundamental harmonic of self-oscillations, it makes sense to be interested only in this harmonic at the output of the nonlinear link. Therefore, we will expand the output oscillations into a Fourier series and discard the higher harmonics. As a result we get:
;
; (12.3)
;
.
Let us rewrite expression (12.2) in a form more convenient for subsequent use, substituting into it the following expressions for and obtained from (12.1):
Substituting these expressions into (12.2), we will have:
(12.4)
. (12.5)
The following notations are introduced here:
. (12.6)
Differential equation(12.5) is valid for a sinusoidal input signal (12.1) and determines the output signal of the nonlinear link without taking into account higher harmonics.
The coefficients in accordance with expressions (12.3) for the Fourier coefficients are functions of the constant component, amplitude A and the frequency of self-oscillations at the input of the nonlinear link. At fixed A, and equation (12.5) is linear. Thus, if we discard higher harmonics, then for a fixed harmonic signal the original nonlinear link can be replaced by an equivalent linear one, described by equation (12.5). This replacement is called harmonic linearization .
In Fig. Figure 12.4 conventionally shows a diagram of this link, consisting of two parallel links.
Rice. 12.4. Equivalent linear element obtained as a result of harmonic linearization.
One link () passes the constant component, and the other - only the sinusoidal component of self-oscillations.
The coefficients are called harmonic linearization coefficients or harmonic transfer coefficients: - transmission coefficient of the constant component, and - two transmission coefficients of the sinusoidal component of self-oscillations. These coefficients are determined by nonlinearity and values and according to formulas (12.3). There are ready-made expressions defined by these formulas for a number of typical nonlinear links. For these and, in general, all inertia-free nonlinear links, the quantities do not depend on and are functions only of the amplitude A And .
When a harmonic signal is applied to the input of a linear system
A harmonic signal is also established at the output of the system, but with a different amplitude and phase shifted relative to the input. If a sinusoidal signal is applied to the input of a nonlinear element, then periodic oscillations are formed at its output, but their shape is significantly different from sinusoidal ones. As an example in Fig. Figure 8.17 shows the nature of the change in the output variable of a nonlinear element with a relay characteristic (8.14) when sinusoidal oscillations (8.18) arrive at its input.
Expanding the periodic signal at the output of a nonlinear element into a Fourier series, we represent it as the sum of a constant component and infinite number harmonic components:
,
(8.19)
Where –
constant coefficients of the Fourier series; – frequency of oscillations of the first harmonic (fundamental frequency), equal to the frequency of input sinusoidal oscillations; T - the period of oscillation of the first harmonic, equal to the period of the input sinusoidal oscillations.
The output signal of the nonlinear element is fed to the input of the linear part of the ACS (see Fig. 8.1), which, as a rule, has significant inertia. In this case, the high-frequency components of the signal (8.19) practically do not pass to the output of the system, i.e. the linear part is a filter in relation to high-frequency harmonic components. In this regard, and also taking into account that the amplitudes of the harmonic components in decrease with increasing harmonic frequency, for an approximate estimate of the output value of the nonlinear element, in a large number of cases it is enough to take into account only the first harmonic component in.
Consequently, in the absence of a constant component in the output oscillations, expression (8.19) can be approximately written as:
Expressing the function from formula (8.20) and from the derivative 
– function 
, we transform expression (8.20) as follows:
.
(8.21)
Thus, the nonlinear dependence of the output quantity on the input quantity in a nonlinear element is approximately replaced by a linear dependence described by expression (8.21).
Having performed the Laplace transform in expression (8.21), we obtain:
As for continuous links, we introduce into consideration transfer function of a nonlinear harmonically linearized element , as the ratio of the image of the output quantity to the image of the input quantity:
.
(8.22)
Table 8.1
Harmonic linearization coefficients for typical nonlinearities
|
Static characteristic of a nonlinear element | ||
|
Linear characteristic with dead band |
| |
|
Linear characteristic with limitation |
| |
|
Linear characteristic with deadband and limiting |
| |
|
"Backlash" characteristic |
| |
|
Ideal relay characteristic | ||
|
Unambiguous relay characteristic with dead band |
| |
|
Ambiguous relay characteristic with dead zone |
|
|
|
Cubic parabola: | ||
|
Characteristic "hysteresis loop" |
|
|
The transfer function of a nonlinear element has a significant difference from the transfer function of a linear system, in that it depends on the amplitude and frequency of the input signal.
We write expression (8.22) in the form:
q(A) + q 1 (A), (8.23)
Where q(A),q 1 (A)– harmonic linearization coefficients, defined as the ratio of the coefficients of the Fourier series for the first harmonic of the output oscillations to the amplitude of the input oscillations:
q(A) = q 1 (A) = . (8.24)
Replacing in expression (8.23) r on , we obtain an expression for complex transmission coefficient of a nonlinear element :
q(A) +j q 1 (A), (8.25)
which is an analogue of the AFC for a linear link.
As an example, let us define an expression for the complex transmission coefficient of a nonlinear element with a relay static characteristic (8.14). Fourier series coefficients A 1 And B 1 for the specified nonlinearity are equal to:
B 1 .
Obviously, the coefficient B 1 will be equal to zero for any nonlinear element with odd-symmetric static nonlinearity.
Where - transfer function of the linear part of the system; - transfer function of a nonlinear element after its linearization.
If 
, then expression (8.26) can be written as:
Replacing in expression (8.27) r on , we obtain a complex expression in which it is necessary to distinguish the real and imaginary parts:
[ q(A) +j q 1 (A) ] . (8.28)
In this case, we write the condition for the occurrence of periodic oscillations in a system with frequency and amplitude:
(8.29)
If the solutions of system (8.29) are complex or negative, the regime of self-oscillations in the system is impossible. The presence of positive real solutions for and indicates the presence of self-oscillations in the system, which must be checked for stability.
As an example, we will find the conditions for the occurrence of self-oscillations in an automatic control system if the transfer function of its linear part is equal to:
(8.30)
and a nonlinear element of the “hysteresis loop” type.
The transfer function of a harmonically linearized nonlinear element (see Table 8.1) has the form:
.
(8.31)
Substituting expressions (8.30) and (8.31) into expression (8.26) and replacing r on , we find an expression for:
From here, in accordance with expression (8.29), we obtain the following conditions for the occurrence of self-oscillations in the system:
Solving the system of equations (8.29) is usually difficult, since the harmonic linearization coefficients have a complex dependence on the amplitude of the input signal. In addition, in addition to determining the amplitude and frequency, it is necessary to assess the stability of self-oscillations in the system.
The conditions for the occurrence of self-oscillations in a nonlinear system and the parameters of limit cycles can be studied using frequency stability criteria, for example, the Nyquist stability criterion. According to this criterion, in the presence of auto-oscillations, the amplitude-phase characteristic of an open-loop harmonically linearized system is equal to
passes through the point (-1, j0). Therefore, for and the following equality holds:
.
(8.32)
The solution to equation (8.32) regarding the frequency and amplitude of self-oscillations can be obtained graphically. To do this, on the complex plane it is necessary, by changing the frequency from 0 to , to construct a hodograph of the AFC of the linear part of the system and, by changing the amplitude A from 0 to , construct a hodograph of the inverse characteristic of the nonlinear part, taken with a minus sign. If these hodographs do not intersect, then the self-oscillation mode does not exist in the system under study (Fig. 8.18, b).
When hodographs intersect (Fig. 8.18, a), self-oscillations arise in the system, the frequency and amplitude of which are determined by the values of and at the intersection point.
If and - intersect at several points (Fig. 8.18, a), then this indicates the presence of several limit cycles in the system. In this case, oscillations in the system can be stable and unstable.
The stability of the self-oscillatory mode is assessed as follows. The self-oscillation mode is stable if the point on the hodograph of the nonlinear part, corresponding to an amplitude greater than the value at the point of intersection of the hodographs, is not covered by the hodograph of the frequency response of the linear part of the system. Otherwise, the self-oscillatory mode is unstable.
In Fig. 8.18, and the hodographs intersect at points 1 and 2. Point 1 determines the unstable mode of self-oscillations, since the hodograph point corresponding to the increased amplitude is covered by the hodograph of the frequency response of the linear part of the system. Point 2 corresponds to a stable mode of self-oscillations, the amplitude of which is determined by the hodograph and the frequency - by the hodograph.
As an example, let us evaluate the stability of self-oscillations in two nonlinear systems. We will assume that the transfer functions of the linear parts of these systems coincide and are equal:
,
but the nonlinear elements included in them are different. Let the first system include a nonlinear element “ideal relay”, described by system (8.14), and let the second system include a nonlinear element with a static characteristic “cubic parabola”. Using the data from Table 8.1, we get:
In Fig. Figure 8.19 shows the hodographs of these systems together with the hodograph of the AFC of the linear part of the system. Based on the foregoing, it can be argued that in the first system stable self-oscillations with frequency and amplitude arise, and in the second system the self-oscillations are unstable.
