Let us denote by Jmoment of inertia of the pendulum relative to the O axis. Let point C be the center of mass. The force of gravity can be decomposed into two components, one of which is balanced by the reaction of the axis. The pendulum begins to move under the influence of another component, a quantity which:

For small angles sin a » a and expression (1) we write:

The minus sign means that the force is directed in the direction opposite to the deviation of the pendulum from the equilibrium position.

The basic equation for the dynamics of rotational motion for a physical pendulum will be written:

Moment of force relative to the O axis taking into account (2):

Where l– distance from the center of mass C to the O axis.

Angular acceleration of the pendulum:

Putting (4) and (5) into equation (3), we get:

where

Having designated

we get:

In structure, equation (6) is a differential equation of harmonic oscillations with a cyclic frequencyw . The period of oscillation of a physical pendulum is equal to:

Hence the moment of inertia of a physical pendulum:

Magnitude

is called the reduced length of a physical pendulum, equal to length a mathematical pendulum having the same period of oscillation as the physical one, i.e.

Point O 1 lying on a straight line drawn through the suspension point O and the center of mass C, at a distance of the given lengthl 0 from rotation axis, is called the center of swing of the pendulum (Fig. 1). The center of swing always lies below the center of mass. The suspension point O and the swing center O 1 are conjugate with each other, i.e. moving the suspension point to the center of swing does not change the period of oscillation of the pendulum. The suspension point and the swing center are reversible, and the distance between these points is the reduced lengthl 0 one of the types of physical pendulum, the so-called reversible pendulum.

Let us denote by J 0 moment of inertia of a pendulum about an axis passing through its center of mass. Based on Steiner's theorem, the moment of inertiaJrelative to any axis parallel to the first:

Where m– mass of the pendulum,l– distance between axes.

Then, when the pendulum is suspended from the suspension point O, the period of oscillation is:

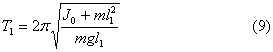
and when suspended by the swing center O 1, when the pendulum is in an inverted position, the period is:

Where l 2 And l 1 – the distance between the center of mass and the corresponding axes of vibration.

From equations (9) and (10):

where:

Formula (11) remains valid when the pendulum oscillates relative to two arbitrary axes O and O /, not necessarily conjugate, but located along different sides from the center of mass of the pendulum.

Description of the operating setup and measurement method.

To determine the acceleration of gravity, the FP-1 device is used (Fig. 2),

consisting of a wall bracket 1, on which 2 support prism cushions are mounted and a physical pendulum, which is a homogeneous metal rod 11, on which lentils 5 and 9 are attached. Lentil 9 is fixed rigidly and is motionless. The lentil 5, located at the end of the rod, can move along a scale 3 with a vernier 4 and is fixed in the desired position with a screw 6. The pendulum can be suspended on support prisms 7 and 10. The device includes a special stand for determining the position of the center of mass of the pendulum. By moving the lentil 5, it is possible to achieve equality of periods of oscillation of the pendulum when hanging it on the support prisms 7 and 10, and then the oscillation axes become conjugate, the distance between the support prisms becomes equal to the reduced length of the physical pendulum.

The magnitude of the acceleration due to gravity is determined based on formula (11). The experiment comes down to measuring quantities T 1 , T 2 , l 1 , l 2 . Formula (8) is the starting point for determining the moment of inertia of a physical pendulum.

Work progress

1) Determination of gravity acceleration .

1. Hang the pendulum on the support prism 7, deflect it at a small angle and measure the time with a stopwatcht 1 30-50 complete vibrations. The experiment is repeated at least 5 times and the average time value is found < t 1 > selected number of oscillations.

2. Determine the period of oscillation:

Where n– number of oscillations.

3. To find the position of the center of mass of the pendulum, remove it from the support prism pads and balance it on the horizontal edge of the prism mounted on the table until the moments of gravity acting on the right and left parts of the pendulum will be equal. In the case of equilibrium, the center of mass of the pendulum will be located in the rod opposite the fulcrum. Without removing the pendulum from the edge of the prism, measure the distance with a rulerl 1 between support 7 and the center of mass.

4. Turning the pendulum over, hang it on the supporting prism 10. Select the same number of oscillationsnand repeat the experiment at least 5 times, find the period of oscillation:

In this case, the measured values ​​of periods T 1 and T 2 should differ by no more than 5%

5. Find distancel 2 between the edge of the supporting prism 10 and the center of mass:l 2 = l 0 – l 1 where l 0 – the distance between the ribs of the supporting prisms 7 and 10 (for this penduluml 0 =0.730m).

6. Calculate the average value < g> according to formula (11)

7. The absolute error of the result is estimated based on the tabular value of the desired valueg tablefor the latitude of Bratsk. Find the relative error.

8. The results of measurements and calculations are recorded in Table 1.

Table 1

2) Determination of the moment of inertia of a physical pendulum.

1. Find the average value of the moment of inertia of a physical pendulumJrelative to the axis of vibration according to formula (8). For oscillations of a pendulum suspended on support 10, T = T 2 andl = l 2. Pendulum mass m= 10.65kg.

2. Using the method of calculating the errors of indirect measurements, find the absolute error of the result DJ.

3. Data from the measurement and calculation results are entered into Table 2.

Table 2

Questions for permission to work

1. What is the purpose of the work?

2. What is a physical pendulum? What type of pendulum is called a reversible pendulum?

3. Write down the formula for the period of oscillation of a physical pendulum and explain physical meaning quantities included in it. Under what conditions is this formula valid?

4. Describe the working setup and the experimental procedure.

Questions to protect your job

1. Derive a formula for the period of oscillation of a physical pendulum.

2. Obtain a differential equation for harmonic oscillations of a physical pendulum and provide its solution.

3. What is the reduced length of a physical pendulum?

4. State Steiner's theorem.

5. Derive the working formula:

to determine the acceleration of free fall;

to determine the moment of inertia of a physical pendulum.

6. Obtain a formula for calculating the relative error using the differential methodDJ/ Jand indicate ways to improve the accuracy of the experimental result.

A physical pendulum is a rigid body capable of oscillating around a fixed point that does not coincide with its center of inertia. In the equilibrium position, the center of inertia of the pendulum C is located under the suspension point of the pendulum O, on the same vertical (Fig. 50). When the pendulum deviates from the equilibrium position by an angle α, a rotational moment arises, tending to return the pendulum to the equilibrium position. This moment is equal

М = – mglsin(α)

Where m is the mass of the pendulum, and l– the distance between the suspension point and the center of inertia of the pendulum. The “–” sign means that the torque tends to return the pendulum to the equilibrium position, i.e., it is directed in the direction opposite to the change in angle Δα. Having designated the moment of inertia of the pendulum relative to the axis passing through the suspension point by the letter J, you can write:

Let us introduce the notation:

Then for small deviations, when the condition sin(α) ≈ α is satisfied, we obtain the equation of harmonic oscillations:

For small deviations from the equilibrium position, the physical pendulum performs harmonic oscillations, the cyclic frequency of which is determined by formula (137). Accordingly, the period of oscillation of a physical pendulum is equal to:

Physical pendulum

From a comparison of formulas (139) and (134) it follows that a mathematical pendulum with a length

will have the same period of oscillation as the given physical pendulum. The quantity (140) is called the reduced length of the physical pendulum. Thus, the reduced length of a physical pendulum is the length of a mathematical pendulum whose period of oscillation coincides with the period of a given physical pendulum.

The point on the straight line connecting the point of suspension with the center of inertia, lying at a distance of a reduced length from the axis of rotation, is called the center of swing of a physical pendulum (see point O" in Fig. 50).

According to Steiner's theorem, the moment of inertia of a pendulum l can be presented in the form

J = J 0 + ml 2, (141)

Where J 0– moment of inertia about an axis parallel to the axis of rotation and passing through the center of inertia of the pendulum. Substituting (141) into formula (140), we obtain:

From (142) it follows that the reduced length is always greater l, so that the suspension point and the center of swing lie on opposite sides of the center of inertia.

Let us suspend the pendulum at a point coinciding with the center of swing O". In accordance with (142), the reduced length in this case will be equal to

Where l"– the distance between the initial center of swing and the center of inertia of the pendulum. Considering that l" = L – l, expression (143) can be written as follows:

Because J 0 + ml 2 equal to the moment of inertia about the original axis of rotation J, and the same value, according to (140), is equal to the expression mlL, then the numerator of the fraction will be equal to zero. That's why L" = L. This means that when the pendulum is suspended at the center of the swing, the reduced length, and therefore the period of oscillation, will be the same as at the beginning. Consequently, the suspension point and the swing center have the property of reciprocity: when the suspension point is transferred to the swing center, the previous suspension point becomes the new swing center.

This position is called

ROSZHELDOR

State educational institution

"Rostovsky state university means of communication"

(RGUPS)

Determination of the moment of inertia of a physical pendulum

Guidelines for laboratory work in physics

Rostov-on-Don

Ladakin, Yu. N.

Determination of the moment of inertia of a physical pendulum: guidelines for laboratory work in physics /,; Height. state University of Communications. – Rostov n/d, 2007. – 10 p. : ill. – Bibliography: 2 titles.

Contains brief theoretical information on the sections “Oscillations” and “Dynamics” solid" Description and principle of operation are given laboratory installation, the procedure for performing the work and recommended literature. Formulated test questions to consolidate the acquired knowledge.

The guidelines have been approved for publication by the Physics Department of the Russian State University of Pedagogical Engineering. Designed for students of all specialties of the Russian State University of Pedagogical University.

Reviewer: Dr. Phys.-Math. sciences, prof. (RGUPS)

Educational edition

DETERMINATION OF THE MOMENT OF INERTIA OF A PHYSICAL PENDULUM

Guidelines for laboratory work in physics

Editor

Technical editing and proofreading

Signed for publication on 12/28/07. Format 60´84/16.

Newsprint paper. Risography. Conditional oven l. 0.58.

Academic ed. l. 0.53. Circulation 50 copies. Ed. No. 58. Order No.

Rostov State Transport University.

Risography RGUPS.

University address: 344038, Rostov n/D, pl. Rostov Rifle Regiment People's Militia, 2.

Ó Rostov State Transport University, 2007

Devices and accessories: Oberbeck pendulum, test body (disk), electronic stopwatch, caliper, ruler, screwdriver.

Purpose of the work: determination of the moment of inertia of a physical pendulum by experimental and computational methods using Steiner’s theorem.

The moment of inertia is physical quantity, which quantitatively characterizes the inertial properties of a body during its rotational motion. The inertia of rotation of a rigid body depends not only on the mass of the body itself, but also on the distribution of this mass in space relative to the axis of rotation.

The moments of inertia of geometrically symmetrical bodies are relatively simple to calculate. Analytical calculation of the moments of inertia of bodies free form is a cumbersome task that requires computational experience.

A solid body of arbitrary shape that oscillates about an axis passing through the suspension point (Fig. 1) is called physical pendulum. It is required to determine the moment of inertia of this pendulum.

In a position of balance center of mass https://pandia.ru/text/80/230/images/image006_43.gif" width="40" height="23">.

There are two forces acting on the pendulum: gravity https://pandia.ru/text/80/230/images/image008_41.gif" width="23" height="27"> (we assume that there are no frictional forces and resistance to the movement of the pendulum Let us deflect the pendulum from the vertical by an angle ( corner bias). The further movement of the pendulum, left to itself, can be considered as rotational about an axis coinciding with the axis perpendicular to the plane of the figure.

According to basic law of dynamics rotational movement the angular acceleration of the pendulum () relative to the axis is equal to the ratio of the resulting moment of all forces acting on the pendulum to its moment of inertia relative to the same axis:

. (1)

The moment of the force conventionally shown in is equal to zero (as can be seen from the figure, the arm of this force is equal to zero), and, therefore, the resulting moment of force is equal to the moment of gravity relative to the axis:

, (2)

where: is the mass of the physical pendulum, is the acceleration of free fall, https://pandia.ru/text/80/230/images/image003_53.gif" width="20" height="21"> and the center of mass. The minus sign in formula (2) indicates that the moment of gravity prevents an increase in angular displacement.

For small amplitudes (https://pandia.ru/text/80/230/images/image017_28.gif" width="79" height="27"> and from (1) taking into account (2) we arrive at a linear differential equation 2nd order:

, Where . (3)

This means that small oscillations of a physical pendulum are harmonic With circular frequency And period(for the period phase oscillations changes to ):

. (4)

Using formula (4), you can experimentally determine the moment of inertia of any body by measuring the quantities , and :

. (5)

A physical pendulum can be obtained using Oberbeck pendulum. It consists of a cross made of 4 rods and attached to a bushing that rotates on a rigidly fixed horizontal axis. If a body, for example a disk, is attached to one of the rods, then the resulting system will be a physical pendulum (Fig. 2). The axis of rotation of the resulting pendulum coincides with the center of mass of the Oberbeck pendulum.

Direct use of formula (5) to calculate the moment of inertia of a given pendulum is difficult. This is due to the difficulty of accurately finding both the position of the center of mass and the mass of the entire pendulum.

Let us transform equation (5) to a form with easily measurable parameters. A pendulum is a system of two rigidly connected bodies: unloaded Oberbeck pendulum with mass and homogeneous disk with mass (Fig. 3).

Since relative to the center of mass vector sum moment of mass of the bodies of the system is equal to zero, we obtain:

.

Hence the distance between the axis of rotation and the center of mass of the resulting pendulum is equal to:

. (6)

Let us substitute (6) into (5) and, taking into account that , we obtain a calculation formula for experimentally determining the moment of inertia of the tested physical pendulum:

. (7)

In formulas (6) and (7) #ris3">Fig. 3). The disk is homogeneous - its center of mass coincides with geometric center. All quantities in formula (7) are now quite easy to measure.

On the other hand, the moment of inertia of the pendulum can be calculated if the moment of inertia of the unloaded Oberbeck pendulum is known (relative to the axis). Indeed, due to the property additivity moment of inertia we have:

,

where is the moment of inertia of a disk of radius , calculated using the Huygens-Steiner theorem relative to the axis ():

.

Thus, the formula for calculating the moment of inertia of the pendulum we are testing takes the form:

. (8)

1 A disk of known mass https://pandia.ru/text/80/230/images/image033_17.gif" width="11 height=23" height="23"> between the axis of rotation and the center of the disk can be obtained from the teacher.

2 By deflecting the pendulum at a small angle, excite its oscillations. Measure the time of ten oscillations. Repeat the measurements 2 more times and record their results in the table.

Educational institution

Department of Mathematics and Physics

PENDULUM

METHODOLOGICAL INSTRUCTIONS FOR LABORATORY WORK No. 1.2

by discipline

"PHYSICS"

Educational institution

"HIGHER STATE COLLEGE OF COMMUNICATIONS"

Department of Mathematics and Physics

DETERMINATION OF THE MOMENT OF INERTIA OF A PHYSICAL

PENDULUM

METHODOLOGICAL INSTRUCTIONS FOR LABORATORY WORK No. 1.2

by discipline

"PHYSICS"

for students of all specialties

DETERMINATION OF THE MOMENT OF INERTIA OF A PHYSICAL

PENDULUM

PURPOSE OF THE WORK: to determine the moment of inertia of a physical pendulum and to study the dependence of the moment of inertia on the position of the center of mass of the pendulum relative to the axis of rotation.

DEVICES AND ACCESSORIES: physical pendulum on a bracket, stopwatch, prism on a stand, scale ruler.

ELEMENTS OF THE THEORY

Periodic displacements of a body relative to some stable position (equilibrium position) are called oscillatory movement or simple vibrations. Oscillatory movements in general represent complex physical processes. The study of vibrations serves as the basis for a number of applied disciplines (acoustics, machine theory, seismology, etc.).

The simplest type of vibration is harmonic oscillatory motion. Harmonic vibrations of a body occur when a force is applied to it that is proportional to the displacement, i.e. . This force is called restoring. The nature of the restoring force can be different (elastic force, gravity, etc.) With harmonic motion, the dependence of the path (displacement ) from time expressed by the sine or cosine function:

,

Where - maximum displacement of the body from the equilibrium position (amplitude),

- circular or cyclic frequency,

- time of one complete oscillation (period),

- initial phase of oscillation .

The acceleration of a body performing harmonic oscillations is proportional to the displacement and is always directed towards equilibrium, i.e. for each moment of time offset and acceleration have opposite signs:

. (1)

Harmonic oscillations are performed by pendulums under the influence of gravity if the angles of deviation from the vertical position (equilibrium position) are small. Pendulums can be simple or complex. A small body (material point) suspended on a long thread, the tension and weight of which can be neglected, is called simple or mathematical pendulum. A solid body of arbitrary shape, fixed on a horizontal axis that does not pass through the center of gravity, is a complex or physical pendulum.

Any solid body can be considered as a collection of invariably connected material points with masses
,
, . . .,
.

When a physical pendulum deviates from its equilibrium position by an angle (Fig. 1) each of its elements will be affected by the moment of gravity relative to the axis of rotation . The sum of the moments of all these forces is equal to the moment of the resultant forces of gravity
, applied to the center of gravity of the pendulum (point ).

Under the influence of the moment of gravity, the pendulum begins to oscillate with angular acceleration
.

If we denote the distance from the axis of rotation to the center of gravity through , then the moment of gravity
would be expressed like this:

or at small angles

, (2)

Where - shoulder strength
,

- mass of the pendulum,

- acceleration of free fall of a body in a given place.

When a pendulum oscillates, its center of gravity moves along an arc of a circle, therefore the equation of Newton's second law for rotational motion is also applicable for a pendulum. It will be written in the form:

, (3)

Where ‑ moment of inertia of the body about the axis of rotation .

Moment of inertia material point called the product of mass (
)per distance squared ( ) from the axis of rotation to it (
). The moment of inertia of a body is equal to the sum of the moments of inertia of its particles relative to the same axis, that is

.

Substituting into equation (3) the value
and solving it with respect to angular acceleration, we get

, (4)

Equation (4) differs from equation (1) only in that it includes angular quantities instead of linear ones.

From a comparison of equations (1) and (4) it follows that
or
, from which we obtain the formula for the period of oscillation of a physical pendulum:

. (5)

From the formula for the period of oscillation of a physical pendulum (5) we find its moment of inertia:

, (6)

Where
- period of oscillation of the pendulum.

This expression is a calculation formula for determining the moment of inertia of a physical pendulum.

EXPERIMENTAL METHOD AND DESCRIPTION OF THE INSTALLATION

The physical pendulum in this work consists of a steel rod

ОD, on which a massive cylindrical body B is attached with screws (Fig. 2). When the support screws are released, body B can be moved along the rod and, therefore, the position of the center of gravity of the pendulum can be changed.

To suspend the pendulum, use a special bracket on which the pendulum is suspended at the point .

To find the center of gravity of the pendulum (point ) is a special prism mounted on a stable stand. The pendulum is placed horizontally on the edge of this prism and, observing the balancing, a position is found in which the moments of gravity acting on the right and left parts of the pendulum will be equal (Fig. 3). In this position, the center of gravity of the pendulum will be located in the rod opposite the fulcrum. Distance
determined using a scale bar.

PROCEDURE FOR PERFORMANCE OF THE WORK

etc. For , And r 3.

Addiction from depicted graphically in the selected coordinate system, and the value is plotted on the horizontal axis (m), and on the vertical (kg m 2 ).

TEST QUESTIONS

Definition of a physical pendulum.

Determination of the moment of inertia of a material point and the moment of inertia of a body.

Give 2 definitions of the moment of force (through the distance from the center of gravity to the axis of rotation and through the arm of the force).

Write down the second law of dynamics for the motion of a pendulum and derive a working formula for the period of oscillation of a physical pendulum.

Wind the suspension thread around the pendulum axis and secure it.

Check whether the lower edge of the ring corresponds to the zero of the scale on the column. If not, unscrew the top bracket and adjust its height. Screw the top bracket.

Press the “START” button of the millisecond watch (cell phone).

At the moment the pendulum passes the bottom point, stop the millisecond watch.

Wind the suspension thread around the pendulum axis, making sure that it is wound evenly, one turn next to the other.

Fix the pendulum, making sure that the thread in this position is not too twisted.

Record the measured value of the time the pendulum falls.

Define timing n= 10 times.

Determine the value of the average time of fall of the pendulum using the formula:

Where n– number of measurements taken, t i– time value obtained in i- that freeze, t– the average value of the time the pendulum falls.

Using the scale on the vertical column of the device, determine the distance covered by the pendulum during the fall.

Using formula (11) and known diameter values d o And d n, determine the diameter of the axis along with the thread wound around it.

Using formula (10), calculate the mass of the pendulum together with the ring imposed in this experiment. The mass values ​​of individual elements are plotted on them.

Using formula (9), determine the moment of inertia of the pendulum.

Compare with theoretical value moment of inertia

I theory = I o + I m,

Where I o– moment of inertia of the axis, I m- moment of inertia of the flywheel, which are calculated using the following formulas:

I o = m o r o 2 / 2; I k = m m r m 2 / 2 .

Practical data:

Pendulum length.

Table 1.

Substituting everything and calculating we get:

I 1 =(0.00090±0.00001) kg*m2.

Conclusion: During the work, the moments of inertia of the pendulum were determined for different lengths of the wound thread and the errors were determined. A comparison of the calculated results and the experimental value reveals a significant difference in the data.

Conclusion: We have determined the experimental and theoretical moments of inertia of the pendulum, which amounted to

and compared them

1.1. The motion of Maxwell's pendulum is an example of the plane motion of a rigid body, in which the trajectories of all its points lie in parallel planes. This motion can be reduced to the translational motion of the pendulum and rotational motion around an axis passing through its center of mass perpendicular to these planes.

This type of motion is widespread in technology: the rolling of a cylinder on a plane, the wheels of a car, the roller of a road car, the movement of a rotating helicopter propeller, etc.

1.2. The purpose of this laboratory work is an experimental acquaintance with the plane motion of a rigid body using the example of Maxwell's pendulum and determining the moment of inertia of the pendulum.

2. BASIC CONCEPTS

2.1. The Maxwell pendulum is a small flywheel. It can be lowered under the influence of gravity and the tension force of threads pre-wound on the axis of the pendulum (Fig. 1). The threads unwind completely during the downward movement. The untwisted flywheel continues to rotate in the same direction and winds the threads around the axis, as a result of which it rises up, while slowing down its movement. Having reached the top point, it begins to go down again.

The flywheel makes a periodically repeating motion, which is why it is called a pendulum. So, the movement of a Maxwell pendulum can be divided into two stages: lowering and rising.

2.2. According to the basic laws of the dynamics of translational and rotational motion (for the corresponding axes), neglecting the forces of friction against the air and the deviation of the threads from the vertical, we write

Where m- mass of the pendulum, I- moment of inertia of the pendulum relative to the axis, - pendulum axis radius, N- tension force of each thread, g- free fall acceleration, a- linear acceleration of the center of mass of the pendulum, - angular acceleration. Due to the inextensibility of the threads

These equations apply to both the first and second stages of the pendulum's motion. The initial conditions at different stages are different: when the pendulum is lowered, the initial speed of its center of mass is zero, and when it rises, it is different from zero.

2.3. From equations (1), (2), (3) it follows

(5)

From the dependence of the path on time for uniformly accelerated motion from zero initial speed you can find the linear acceleration of the pendulum

Where t- time of movement of the pendulum from the top to the bottom point, h- the distance traveled during this time. At we have ; (7)

Note that the directions of linear acceleration and tension forces do not depend on whether the pendulum is moving up or down. During one complete oscillation, the linear velocity changes its direction at the bottom point to the opposite, but the linear acceleration and forces do not change. Angular velocity, on the contrary, does not change its direction, but the moment of force and angular acceleration at the bottom point are reversed.

2.4.When rising upward, the pendulum moves equally slow. Height h2, to which he rises will be less than the one from which he descends h1. The difference in these heights determines the decrease in mechanical energy spent on overcoming the forces of deformation of the threads upon impact and the forces of resistance to movement.

Proportion of lost mechanical energy

(9)

INSTALLATION DESCRIPTION

3.1. The installation diagram is shown in Fig. 2. A column 2 is fixed to the base 1; it holds the upper bracket 3, on which there is an electromagnet 4, a photoelectric sensor 5 and a knob 6 for leveling the pendulum suspension. A second photoelectric sensor 7 is attached to the lower bracket. The Maxwell pendulum flywheel consists of a disk 8 mounted on an axis 9 and a massive ring 10 attached to it. It is suspended on two parallel threads wound on the axis. The pendulum is held in the upper position by an electromagnet. The heights of lowering and raising the pendulum are determined using a millimeter ruler 11 located on the column of the device. Millisecond watch MS 12 is designed for measuring time t movements of Maxwell's pendulum. The start and end of the time counting are carried out automatically using the photo sensors mentioned above.

The moment of inertia of a Maxwell pendulum is determined indirectly.

From equations (6) and (8) it follows that the moment of inertia can be calculated using the formula

Here m– total mass of the pendulum,

m = m O+m d+mK , (11)

Where m O - axle mass, m d - mass of the disk.

4. ORDER OF MEASUREMENTS

4.1. Technical data.

4.1.1. Enter the installation data into the table. 1.

Table 1

4.1.2. Enter into the table. 2 values ​​of masses and diameters of pendulum elements. These data are indicated on the installation.

Table 2

4.3. Determination of the moment of inertia of a Maxwell pendulum.

4.2.2. Wind the suspension threads onto the pendulum axis symmetrically, turn to turn, and fix the pendulum. You should work very carefully.

4.2.3. Release the pendulum and start counting time. Stop the countdown at the bottom point.

4.2.5. Enter the measured value of the time of movement of the pendulum in Table 3. Repeating the operations in paragraphs 4.2.2 and 4.2.3, measure the time 10 more times and enter the data in the table. 3.

Table 3

4.3. Determination of loss of mechanical energy

4.3.1. Use a ruler to determine the height h 1, from which the pendulum descends; enter into the table 3.

4.3.2. Repeat the operations described in paragraphs 4.2.2 and 4.2.3, let the pendulum make five full oscillations, measure the height difference d h. Perform this measurement once and enter its result in the table. 3.

5. PROCESSING OF MEASUREMENT RESULTS

5.1. Determination of the moment of inertia of a Maxwell pendulum.

Calculate the average value of the time of movement of the pendulum and enter it in the table. 3.

Calculate the mean square error in measuring the time of movement of the pendulum

(12)

5.1.3. Calculate absolute random error

D t sl = 2,1D.S.. (13)

5.1.4. Calculate the total absolute error

D t = D t сл + D t inc.(14)

5.1.5. Calculate relative error

Place all calculated values ​​in the table. 3.

5.1.6. Using formula (10), calculate the moment of inertia of the pendulum, substituting its average value.

5.1.7. Calculate the relative error of the moment of inertia of the pendulum

, (16)

Where D m , D r O, D h1- instrument errors of the corresponding quantities, Dt – total absolute error of movement time; m- the total mass of the pendulum, calculated using formula (11).

5.1.8. Based on the received value e J calculate the absolute error value DJ in determining the moment of inertia

DJ = e J J= . (17)

Round DJ to one significant figure, and the values `J to the level of absolute error.

5.1.9. Write the final result in the form

J =`J± D J =(±) kg × m 2 . (18)

5.2. Determination of the loss of mechanical energy during the movement of a Maxwell pendulum.

5.2.1. Formula (9) expresses the fraction of mechanical energy lost during five oscillations of the Maxwell pendulum; for one oscillation the share will be five times less:

6. QUESTIONS submitted for JOB DEFENSE

1. Basic law of dynamics forward movement.

3. How do impulses and axial moment momentum of Maxwell's pendulum at the lowest point of its movement? Explain your reasons.

4. Law of conservation of total energy for Maxwell's pendulum.

5. Find linear and angular velocity pendulum at its lowest point.

6. Moment of inertia of a rigid body (definition). What does its size depend on?

7. Find the ratio of the kinetic energy of translational motion to the kinetic energy of rotational motion for a given Maxwell pendulum.

8. How do linear and angular accelerations change during the period of motion of the Maxwell pendulum?

9. Momentum and axial angular momentum of a rigid body.

10. Estimate the tension of the threads when the pendulum passes the lowest point (the duration of the “blow” in it is taken equal to Dt"0.05c).

11. How will the time of movement of the pendulum change if the radius of its axis is doubled?

12. Kinetic energy translational and rotational motion of a rigid body.

13. Calculation of the moment of inertia of a disk with a radius R, mass m

14. What forces and torques act on the Maxwell pendulum during its movement? How do they change over the period?

15. Calculation of the moment of inertia of a ring with a radius R, mass m relative to an axis passing through the center perpendicular to its plane.

16. Obtain formula (10) based on the law of conservation of mechanical energy. (Please note that for the Maxwell pendulum E to vr >>E to post).

17. In which part of the pendulum’s motion, upper or lower, is the loss of mechanical energy greater? Explain the reasons.