1°

1°. Az érintősík és a normál egyenlete a felület explicit meghatározása esetén.

Tekintsük két változó függvényének parciális deriváltjainak egyik geometriai alkalmazását. Hagyja a függvényt z = f (x ;y) ponton differenciálható (x 0; y 0) valamilyen területet DÎ R 2. Vágjuk le a felületet S, a funkciót reprezentálja z, repülőgépek x = x 0És y = y 0(11. ábra).

Repülőgép X = x 0 metszi a felületet S valamilyen vonal mentén z 0 (y ), melynek egyenletét az eredeti függvény kifejezésébe behelyettesítve kapjuk z ==f (x ;y) helyett X számok x 0. Pont M 0 (x 0;y 0,f (x 0;y 0)) görbéhez tartozik z 0 (y). A differenciálható funkció miatt z pontban M 0 funkció z 0 (y) ponton is differenciálható y =y 0 . Ezért a sík ezen a pontján x = x 0 a görbére z 0 (y)érintőt lehet húzni l 1.

Hasonló érvelés végrehajtása a szakaszra vonatkozóan at = y 0,építsünk érintőt l 2 a görbére z 0 (x) pontban X = x 0 - Közvetlen 1 1 És 1 2 nevű síkot határozzuk meg érintő sík a felszínre S pontban M 0.

Készítsük el az egyenletét. Mivel a sík áthalad a ponton Mo(x 0;y 0;z 0), akkor az egyenlete úgy írható fel

A(x - xo) + B(y - yo) + C (z - zo) = 0,

ami így átírható:

z -z 0 = A 1 (x - x 0) + B 1 (y - y 0) (1)

(az egyenletet -C-vel osztva és jelölve ).

Meg fogjuk találni A 1és B 1.

Érintőegyenletek 1 1 És 1 2 úgy néz ki

illetőleg.

Tangens l 1 a síkban fekszik , ezért az összes pont koordinátái l 1 kielégíti az (1) egyenletet. Ez a tény leírható egy rendszer formájában

Ezt a rendszert B 1 vonatkozásában feloldva azt kapjuk, hogy hasonló érvelést hajtunk végre az érintőre l 3, könnyű megállapítani, hogy .

Az értékek helyettesítése A 1és B 1-et az (1) egyenletbe, megkapjuk a kívánt érintősík egyenletet:

Ponton átmenő egyenes M 0és a felület ezen pontjában megszerkesztett érintősíkra merőlegesen annak nevezzük normál.

Egy egyenes és egy sík merőlegességének feltételével könnyen beszerezhető kanonikus egyenletek normál:

Megjegyzés. Az érintősík és a felület normális képleteit a felület közönséges, azaz nem speciális pontjaira kapjuk. Pont M 0 felületnek nevezzük különleges, ha ezen a ponton minden parciális derivált nulla vagy legalább az egyik nem létezik. Nem vesszük figyelembe az ilyen szempontokat.

Példa. Írjon fel egyenleteket az érintősíkra és a felület normális pontjára! M(2; -1; 1).

Megoldás. Keressük meg ennek a függvénynek a parciális deriváltjait és azok értékét az M pontban

Innentől kezdve a (2) és (3) képlet alkalmazásával a következőket kapjuk: z-1=2(x-2)+2(y+1) vagy 2х+2у-z-1=0- érintősík egyenlet és - normál egyenletek.

2°. Az érintősík és a normál egyenlete a felület implicit meghatározása esetén.

Ha a felület S egyenlet adja meg F (x ; y;z)= 0, akkor a (2) és (3) egyenlet, figyelembe véve, hogy a parciális deriváltok egy implicit függvény deriváltjaként is megtalálhatók.

1. definíció : A felület érintősíkja egy adott P pontban (x 0, y 0, z 0) a P ponton áthaladó sík, amely tartalmazza a P pontban megszerkesztett összes érintőt ezen a felületen a P ponton áthaladó összes lehetséges görbére.

Adja meg az s felületet az egyenlet F (X, at, z) = 0 és pont P (x 0 , y 0 , z 0) ehhez a felülethez tartozik. Válasszunk ki egy görbét a felületen L, áthaladva a ponton R.

Hadd X = X(t), at = at(t), z = z(t) - parametrikus egyenletek vonalak L.

Tegyük fel, hogy: 1) függvény F(X, at, z) ponton differenciálható Rés ezen a ponton nem minden parciális deriváltja egyenlő nullával; 2) függvények X(t), at(t), z(t) is megkülönböztethetők.

Mivel a görbe az s felülethez tartozik, a görbe bármely pontjának koordinátái a felület egyenletébe behelyettesítve azonossággá alakítják. Így az azonos egyenlőség igaz: F [x(t), at(t), z (t)]= 0.

Ennek az azonosságnak a megkülönböztetése a változóhoz képest t, a láncszabály segítségével új azonos egyenlőséget kapunk, amely a görbe minden pontján érvényes, beleértve a pontot is. P (x 0 , y 0 , z 0):

A P pont feleljen meg a paraméter értékének t 0, vagyis x 0 = x (t 0), y 0 = y (t 0), z 0 = z (t 0). Ezután a pontban számított utolsó összefüggés R, a formát veszi fel

Ez a képlet két vektor skaláris szorzata. Az első egy konstans vektor

független a felületi görbe megválasztásától.

A második vektor a pontban érintő R a vonalhoz L, ami azt jelenti, hogy a felület vonalválasztásától függ, vagyis változó vektor.

A bevezetett jelöléssel az egyenlőség a következő:

írjuk át hogyan.

Jelentése a következő: a skaláris szorzat egyenlő nullával, ezért a vektorok merőlegesek. Egy ponton átmenő összes lehetséges görbe kiválasztása R az s felületen különböző érintővektorokat szerkesztünk a pontban R ezekre a sorokra; a vektor nem függ ettől a választástól, és egyikre merőleges lesz, vagyis minden érintővektor ugyanabban a síkban helyezkedik el, amely definíció szerint érinti az s felületet, és a pont R ebben az esetben érintőpontnak nevezzük. A vektor a felület normál irányának vektora.

Meghatározás 2: A P pontban lévő s felület normálja a P ponton átmenő egyenes, amely merőleges az ebben a pontban megszerkesztett érintősíkra.

Bebizonyítottuk, hogy létezik egy érintősík, és ennek következtében a felület normálja. Írjuk fel az egyenleteiket:

A P (x0, y0, z0) pontban megszerkesztett érintősík egyenlete az s felülethez, amelyet az F(x, y, z) = 0 egyenlet adott;

Egy pontban megszerkesztett normális egyenlete R a felszínre s.

Példa: Határozzuk meg a parabola forgásával alkotott felület egyenletét:

z 2 = 2p (y +2)

az y tengely körül számítsuk ki, feltéve, hogy a pont M(3, 1, - 3) a felszínhez tartozik. Határozzuk meg az M pontban lévő felület normálsík és érintősík egyenleteit!

Megoldás. A forgási felület írásának szabályát használva a következőket kapjuk:

z 2 + x 2 = 2p (y +2) .

Ebbe az egyenletbe behelyettesítve az M pont koordinátáit, kiszámítjuk a p paraméter értékét: 9 + 9 = 2р(1 + 2) . Rögzítjük a ponton áthaladó forgásfelület végső képét M:

z 2 + x 2 = 6(y +2).

Most a képletek segítségével megtaláljuk a normál és az érintősík egyenleteit, amelyekhez először kiszámítjuk a függvény parciális deriváltjait:

F(x, y) = z 2 + x 2- 6 (y +2):

Ekkor az érintősík egyenlete felveszi a formát 6 (x - 3) - 6 (y - 1) - 6 (z + 3) = 0 vagy x-y-z-5 = 0;

Tekintsük több változó függvényének deriváltjának geometriai alkalmazásait. Adjunk meg implicit módon két változó függvényét: . Ezt a függvényt a definíciós tartományában egy bizonyos felület képviseli (5.1. szakasz). Vegyünk egy tetszőleges pontot ezen a felületen , amelyben mindhárom , , parciális derivált létezik és folytonos, és legalább az egyik nem egyenlő nullával.

Az ilyen jellemzőkkel rendelkező pontot ún rendes felszíni pont. Ha a fenti követelmények közül legalább az egyik nem teljesül, akkor a pont hívásra kerül különleges felszíni pont.

A felületen kiválasztott ponton keresztül sok görbe rajzolható, amelyek mindegyikének lehet érintője.

Meghatározás 5.8.1 . Azt a síkot, amelyben a felület egy bizonyos ponton áthaladó vonalainak összes érintője található, a pontban a felület érintősíkjának nevezzük. .

költeni adott repülőgép elég két érintővonal, azaz két görbe a felületen. Ezek lehetnek egy adott felület síkokkal történő vágása eredményeként kapott görbék (5.8.1. ábra).

Írjuk fel a felület és a sík metszéspontjában fekvő görbére az érintővonal egyenletét. Mivel ez a görbe a koordinátarendszerben található, a pontban lévő érintő egyenlete a 2.7. szakasz szerint a következőképpen alakul:

. (5.8.1)

Ennek megfelelően a koordinátarendszerben ugyanazon a ponton lévő felület és sík metszéspontjában lévő görbe érintőjének egyenlete a következő:

. (5.8.2)

Használjuk a kifejezést egy implicit módon megadott függvény deriváltjára (5.7. szakasz). Akkor na. Ezeket a származékokat (5.8.1) és (5.8.2) behelyettesítve kapjuk, hogy:

; (5.8.3)

. (5.8.4)

Mivel az eredményül kapott kifejezések nem mások, mint egyenesek egyenletei kanonikus forma(15. tétel), akkor az (5.8.3)-ból megkapjuk az irányvektort , és (5.8.4) – . vektoros alkotás normális vektort ad az adott érintővonalra, és ennek következtében az érintősíkra:

Ebből következik, hogy a felület érintősíkjának egyenlete a pontban a következő űrlappal rendelkezik (14. tétel):

Meghatározás 5.8.2 . Egy ponton keresztül húzott egyenes Az érintősíkra ezen a ponton merőleges felületet a felület normáljának nevezzük.

Mivel a felület normáljának irányvektora egybeesik az érintősík normáljával, a normálegyenlet a következőképpen alakul:

.

Skaláris mező

Adjunk meg egy régiót a térben, amely ennek a területnek egy részét vagy egészét foglalja el. Legyen ennek a területnek minden pontja valamilyen törvény szerint egy bizonyos skaláris mennyiséghez (számhoz) rendelve.

Meghatározás 5.9.1 . Skalármezőnek nevezzük azt a területet a térben, amelynek minden pontja egy jól ismert törvény szerint hozzá van rendelve egy bizonyos skaláris mennyiséghez..

Ha a területhez valamilyen koordinátarendszer van társítva, például derékszögű derékszögű rendszer, akkor minden pont megkapja a saját koordinátáit. Ebben az esetben a skaláris mennyiség a koordináták függvényévé válik: a síkon – , háromdimenziós térben – . Magát a mezőt leíró függvényt gyakran skaláris mezőnek nevezik. A tér méretétől függően a skaláris mező lehet lapos, háromdimenziós stb.

Hangsúlyozni kell, hogy a skalármező nagysága csak a pont helyzetétől függ a régióban, de nem függ a koordinátarendszer megválasztásától.

Meghatározás 5.9.2 . Stacionáriusnak nevezzük azt a skaláris mezőt, amely csak egy pont helyzetétől függ a régióban, de nem függ az időtől..

A nem stacionárius, azaz időfüggő skalármezőket ebben a részben nem vesszük figyelembe.

A skaláris mezőkre példa a hőmérsékleti mező, a légkör nyomásmezője és az óceánszint feletti magasságmező.

Geometriailag a skaláris mezőket gyakran úgynevezett vonalak vagy szintfelületek segítségével ábrázolják.

Meghatározás 5.9.3 . A tér azon pontjainak halmaza, amelyekben a skalármező található azonos jelentésű, síkfelületnek vagy ekvipotenciális felületnek nevezzük. Skalármező esetén ezt a halmazt szintvonalnak vagy ekvipotenciálvonalnak nevezzük.

Nyilvánvaló, hogy a szintfelületi egyenletnek megvan a formája , szintvonalak – . Azáltal, hogy ezekben az egyenletekben megadjuk az állandót különböző jelentések, felületek vagy szintvonalak családját kapjuk. Például, (különböző sugarú egymásba ágyazott gömbök) vagy (ellipszisek családja).

A fizika szintvonalaira példák az izotermák (egyenlő hőmérsékletű vonalak), az izobárok (egyenlő nyomású vonalak); geodéziából - egyenlő magasságú vonalak stb.

Mégpedig arról, amit a címben lát. Lényegében ez egy „térbeli analóg” érintő problémák kereséseÉs normálisak egy változó függvényének grafikonjára, és ezért nem merülhet fel nehézség.

Kezdjük az alapvető kérdésekkel: MI AZ érintősík és MI A normál? Sokan az intuíció szintjén értik ezeket a fogalmakat. A legegyszerűbb modell, ami eszünkbe jut, egy golyó, amelyen egy vékony lapos kartonlap fekszik. A karton a lehető legközelebb van a gömbhöz, és egyetlen ponton érinti. Ezenkívül az érintkezési ponton egy egyenesen felfelé szúró tűvel rögzítik.

Elméletileg van egy meglehetősen zseniális definíciója az érintősíknak. Képzelj el egy ingyenes felületés a hozzá tartozó pontot. Nyilván sok minden átmegy a lényegen térbeli vonalak, amelyek ehhez a felülethez tartoznak. Kinek milyen egyesületei vannak? =) ...személy szerint egy polipot képzeltem el. Tegyük fel, hogy minden ilyen sor rendelkezik térbeli érintő pontban.

1. definíció: érintő sík egy ponton a felszínre – ez az repülőgép, amely egy adott felülethez tartozó és a ponton átmenő görbék érintőit tartalmazza.

2. definíció: normál egy ponton a felszínre – ez az egyenes, áthaladva ezt a pontot merőleges az érintősíkra.

Egyszerű és elegáns. Egyébként, hogy ne halj bele az unalomba az anyag egyszerűsége miatt, kicsit később megosztok veled egy elegáns titkot, amivel elfeledkezhetsz a különféle definíciók összezsúfolásáról EGYSZER ÉS MINDENKINEK.

Konkrét példán keresztül ismerkedjünk meg a munkaképletekkel és a megoldási algoritmussal. A problémák túlnyomó többségében meg kell alkotni az érintősík egyenletet és a normál egyenletet is:

1. példa

Megoldás:ha a felületet az egyenlet adja meg (azaz implicit módon), akkor egy pontban egy adott felület érintősíkjának egyenlete a következő képlettel kereshető meg:

Különös figyelmet fordítok a szokatlan parciális származékokra - azok nem szabad összekeverni Vel egy implicit módon meghatározott függvény parciális deriváltjai (bár a felület implicit módon meg van adva). Ezen származékok megtalálásakor az embernek vezérelnie kell szabályok a három változó függvényének megkülönböztetésére, vagyis ha bármely változóhoz képest megkülönböztetünk, a másik két betűt konstansnak tekintjük:

Anélkül, hogy elhagynánk a pénztárgépet, a részleges származékot a következő helyen találjuk:

Hasonlóképpen:

Ez volt a döntés legkellemetlenebb pillanata, amikor egy hiba, ha nem megengedett, de folyamatosan megjelenik. Azonban van hatékony technika ellenőrizze, hogy miről beszéltem az órán Irányi derivált és gradiens.

Az összes „összetevőt” megtaláltuk, és most gondos helyettesítésről van szó további egyszerűsítésekkel:

– általános egyenlet a kívánt érintősíkot.

Erősen javaslom a megoldás ezen szakaszának ellenőrzését is. Először meg kell győződnie arról, hogy az érintőpont koordinátái valóban megfelelnek a talált egyenletnek:

- igazi egyenlőség.

Most „eltávolítjuk” az együtthatókat általános egyenlet síkokat, és ellenőrizze, hogy egybeesnek vagy arányosak-e a megfelelő értékekkel. Ebben az esetben arányosak. Ahogy emlékszel analitikus geometria tanfolyam, - Ezt normál vektorérintősík, és ő is az útmutató vektor normál egyenes vonal. Komponáljunk kanonikus egyenletek normálok pont- és irányvektor szerint:

Elvileg a nevezők kettővel csökkenthetők, de erre nincs különösebb szükség

Válasz:

Nem tilos az egyenleteket néhány betűvel jelölni, de miért? Itt már nagyon világos, hogy mi az.

A következő két példa erre való önálló döntés. Egy kis „matematikai nyelvforgató”:

2. példa

Határozzuk meg az érintősík és a felület normáljának egyenleteit a pontban!

És egy technikai szempontból érdekes feladat:

3. példa

Írjon fel egyenleteket a felület érintősíkjára és normáljára egy pontban!

A ponton.

Minden esély megvan arra, hogy ne csak összezavarodj, hanem nehézségekbe is ütközz a felvétel során az egyenes kanonikus egyenletei. És a normál egyenletek, amint valószínűleg megérti, általában ebben a formában vannak írva. Bár néhány árnyalat feledékenysége vagy tudatlansága miatt a parametrikus forma több mint elfogadható.

Hozzávetőleges példák a megoldások végső végrehajtására az óra végén.

Van-e érintősík a felület bármely pontjában? Általában véve természetesen nem. A klasszikus példa az kúpfelület és pont - az érintők ezen a ponton közvetlenül kúpos felületet alkotnak, és természetesen nem fekszenek ugyanabban a síkban. Könnyű analitikusan ellenőrizni, hogy valami nincs rendben: .

A másik problémaforrás a tény nemlétezés bármely parciális derivált egy pontban. Ez azonban nem jelenti azt, hogy egy adott pontban nincs egyetlen érintősík.

De ez inkább populáris tudomány volt, mintsem gyakorlatilag jelentős információ, és visszatérünk a sürgető kérdésekhez:

Hogyan írjunk fel egyenleteket az érintősíkra és a normálra egy pontban,
ha a felületet explicit függvény határozza meg?

Írjuk át implicit módon:

És ugyanezeket az elveket alkalmazva parciális származékokat találunk:

Így az érintősík képlet a következő egyenletté alakul:

És ennek megfelelően a kanonikus normálegyenletek:

Ahogy sejtheti, - ezek már „igaziak” két változó függvényének parciális deriváltjai ponton, amit korábban „z” betűvel jelöltünk, és 100500-szor találtuk meg.

Felhívjuk figyelmét, hogy ebben a cikkben elég emlékezni a legelső képletre, amelyből szükség esetén könnyen levezethető minden más (természetesen alapfokú képzettséggel). Pontosan ezt a megközelítést kell alkalmazni az egzakt tudományok tanulmányozása során, pl. minimális információból arra kell törekednünk, hogy maximum következtetéseket és következtetéseket „levonjunk”. A „megfontoltság” és a meglévő tudás segít! Ez az elv azért is hasznos, mert nagy valószínűséggel megmenti Önt egy kritikus helyzetben, amikor nagyon keveset tud.

Nézzük meg a „módosított” képleteket néhány példával:

4. példa

Írjon egyenleteket a felület érintő síkjára és normáljára! pontban.

Itt van egy kis átfedés a jelölésekkel - most a betű egy pontot jelöl a síkon, de mit tehetsz - ilyen népszerű betű...

Megoldás: állítsuk össze a kívánt érintősík egyenletét a következő képlettel:

Számítsuk ki a függvény értékét a pontban:

Számoljunk I. rendű részszármazékok ezen a ponton:

Így:

óvatosan, ne rohanjon:

Írjuk fel a normális kanonikus egyenleteit a pontba:

Válasz:

És egy utolsó példa a saját megoldásodhoz:

5. példa

Írja fel a pontban lévő felület érintősíkjának és normáljának egyenleteit!

Végső – mert gyakorlatilag az összes technikai pontot kifejtettem, és nincs mit hozzátenni. Még maguk az ebben a feladatban javasolt függvények is unalmasak és monotonok - a gyakorlatban szinte garantáltan találkozunk egy „polinomiával”, és ebben az értelemben a 2. példa exponenssel úgy néz ki, mint egy „fekete bárány”. Egyébként sokkal nagyobb eséllyel találkozik felülettel egyenlet adja megés ez egy másik oka annak, hogy a függvény másodikként került be a cikkbe.

És végül a beígért titok: hogyan kerüljük el a definíciók zsúfoltságát? (Persze nem arra a helyzetre gondolok, amikor egy diák lázasan tömködik valamit vizsga előtt)

Bármely fogalom/jelenség/tárgy meghatározása mindenekelőtt a következő kérdésre ad választ: MI AZ? (kik/olyanok/olyanok). Tudatosan A kérdés megválaszolásakor meg kell próbálnia reflektálni jelentős jelek, határozottan egy adott fogalom/jelenség/tárgy azonosítása. Igen, eleinte kissé nyelvesnek, pontatlannak és feleslegesnek bizonyul (a tanár kijavít =)), de idővel egészen tisztességes tudományos beszéd alakul ki.

Gyakoroljon például a legelvontabb tárgyakon, és válaszoljon a kérdésre: ki az a Cseburaska? Ez nem ilyen egyszerű ;-) Ez " mesefigura nagy fülekkel, szemekkel és barna bundával"? Messze és nagyon távol van a meghatározástól – sosem tudhatod, hogy vannak ilyen tulajdonságokkal rendelkező karakterek... De ez sokkal közelebb áll a definícióhoz: „Cseburaska Eduard Uszpenszkij író által 1966-ban kitalált karakter, aki ... (a fő listák jellegzetes vonásait)» . Figyeld meg, milyen jól indult

Töltse le a Depositfiles oldalról

4. FELÜLETEK ELMÉLETE.

4.1 FELÜLETEGYENLETEK.

Felület be háromdimenziós tér adható:

1) implicit módon: F ( x , y , z ) =0 (4.1)

2) kifejezetten: z = f ( x , y ) (4.2)

3) paraméteresen: (4.3)

vagy:
(4.3’)

hol vannak a skaláris argumentumok
néha görbe vonalú koordinátáknak nevezik. Például a gömb
kényelmes behelyezni gömbi koordináták:
.

4.2 ÉRINTŐSÍK ÉS A FELÜLET NORMÁLIS.

Ha egy egyenes a (4.1) felületen fekszik, akkor pontjainak koordinátái kielégítik a felületi egyenletet:

Ezt az identitást megkülönböztetve a következőket kapjuk:

(4.4)

vagy
(4.4 ’ )

a felület görbéjének minden pontjában. Így a gradiensvektor a felület nem szinguláris pontjaiban (amelyeknél a (4.5) függvény differenciálható és
) merőleges a felület bármely vonalának érintővektoraira, azaz normálvektorként használható az M pontban lévő érintősík egyenletének összeállításához 0 (x 0 , y 0 , z 0 ) felület

(4.6)

és irányvektorként a normál egyenletben:

(4.7)

A felület explicit (4.2) specifikációja esetén az érintősík és a normál egyenlete a következőképpen alakul:

(4.8)

És
(4.9)

A felület parametrikus ábrázolásával (4.3) a vektorok
fekszenek az érintősíkban, és az érintősík egyenlete a következőképpen írható fel:

(4.10)

és vektorszorzatuk iránynormálvektornak tekinthető:

és a normál egyenlet így írható fel:

(4.11)

Ahol
— az M pontnak megfelelő paraméterértékek 0 .

A következőkben arra szorítkozunk, hogy csak olyan felületi pontokat vegyünk figyelembe, ahol a vektorok

nem egyenlő nullával és nem párhuzamos.

4.1. példa Hozzon létre egyenleteket az érintősíkra és a normálra az M pontban 0 (1,1,2) egy forgásparaboloid felületére
.

Megoldás: Mivel a paraboloid egyenlet explicit módon adott, ezért (4.8) és (4.9) szerint meg kell találnunk
az M pontban 0 :

, és az M 0 pontban
. Ekkor az érintősík egyenlete az M pontban A 0 így fog kinézni:

2(x -1)+2(y -1)-(z-2)=0 vagy 2 x +2 y – z - 2=0, és a normál egyenlet
.

4.2. példa Állítson össze egyenleteket az érintősíkra és a normálra a helikoid tetszőleges pontjában
, .

Megoldás. itt ,

Érintősík egyenlet:

vagy

Normál egyenletek:

.

4.3 ELSŐ QUADRATIKUS FELÜLET FORMA.

Ha a felületet az egyenlet adja

majd a görbe
egyenlettel megadható
(4.12)

Sugár vektor differenciál
a görbe mentén, ami megfelel az M ponttól való elmozdulásnak 0 a legközelebbi M ponthoz egyenlő

(4.13)

Mert
az azonos elmozdulásnak megfelelő görbe ívének differenciálja), akkor

(4.14)

Hol .

A (4.14) jobb oldalán lévő kifejezést a felület első másodfokú alakjának nevezik, és óriási szerepet játszik a felületek elméletében.

A differenciálművet integrálomds től kezdve t 0 (az M pontnak felel meg 0 ) a t (megfelel az M pontnak), megkapjuk a görbe megfelelő szakaszának hosszát

(4.15)

Egy felület első másodfokú alakjának ismeretében nemcsak a hosszak, hanem a görbék közötti szögek is megtalálhatók.

Ha du , dv görbe vonalú koordináták különbségei, amelyek egy görbe mentén végtelenül kicsi elmozdulásnak felelnek meg, és
- másrészt figyelembe véve (4.13):

(4.16)

Képlet segítségével

(4.17)

az első másodfokú forma lehetővé teszi a régió területének kiszámítását
felületek.

4.3. példa Egy helikoidon keresse meg a spirál hosszát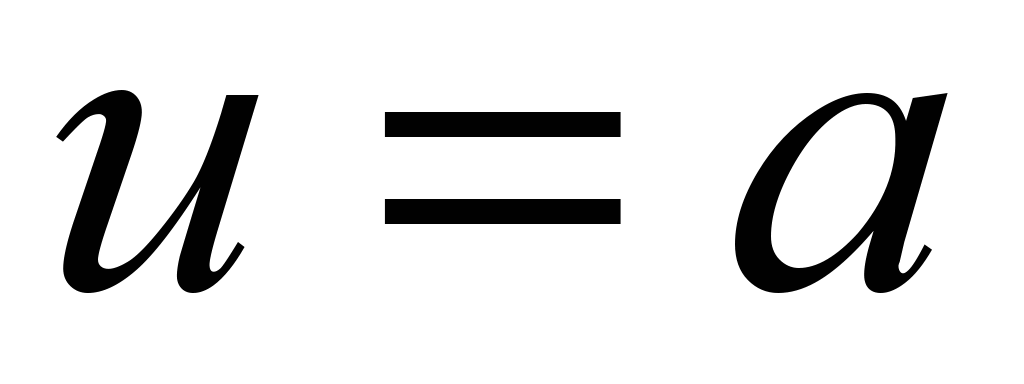
két pont között.

Megoldás. Mert a helixen
, Azt . Keressük a lényeget
első másodfokú forma. Miután kijelölte ésv = t , formában kapjuk meg ennek a csavarvonalnak az egyenletét. Kvadratikus forma:

= - első másodfokú alak.

itt . Ebben az esetben a (4.15) képletben
és ív hossza:

=

4.4 MÁSODIK QUADRATIKUS FELÜLET FORMA.

Jelöljük
- a felületre merőleges egységvektor
:

(4.18) . (4.23)

Egy felületen lévő vonalat görbületi vonalnak nevezünk, ha annak iránya minden pontban a fő irány.

4.6 GEODÉZIKAI VONALOK FELÜLETÉN.

Meghatározás 4.1 . Egy felületen lévő görbét geodetikusnak nevezzük, ha főnormálisa minden pontban, ahol a görbület nem nulla, egybeesik a normállal a felszínre.

A felület minden pontján bármely irányban áthalad, és csak egy geodetikus. Egy gömbön például a nagy körök geodetikusok.

Egy felületparaméterezést félgeodézikusnak nevezünk, ha a koordinátavonalak egyik családja geodetikus elemekből áll, a másik pedig arra merőleges. Például egy gömbön vannak meridiánok (geodézia) és párhuzamosságok.

Egy kellően kis szakaszon lévő geodetikus a legrövidebb a hozzá közel álló, ugyanazokat a pontokat összekötő görbék közül.