Jelöljük azzal Jaz inga tehetetlenségi nyomatéka az O tengelyhez képest Legyen C pont a tömegközéppont. A gravitációs erő két komponensre bontható, amelyek közül az egyiket a tengely reakciója egyensúlyozza ki. Az inga egy másik komponens hatására kezd el mozogni, olyan mennyiségben, amely:

Kis szögeknél bűn a » a és az (1) kifejezést írjuk:

A mínusz előjel azt jelenti, hogy az erő az inga egyensúlyi helyzetétől való eltérésével ellentétes irányba hat.

A forgómozgás dinamikájának alapegyenlete fizikai inga esetén a következő:

Az O tengelyhez viszonyított erőnyomaték, figyelembe véve (2):

Ahol l– távolság a C tömegközépponttól az O tengelyig.

Az inga szöggyorsulása:

Ha a (4)-et és (5)-et a (3) egyenletbe beletesszük, a következőt kapjuk:

ahol

Miután kijelölte

kapunk:

Szerkezetében a (6) egyenlet ciklikus frekvenciájú harmonikus rezgések differenciálegyenlete.w . A fizikai inga rezgési periódusa egyenlő:

Ezért a fizikai inga tehetetlenségi nyomatéka:

Nagyságrend

a fizikai inga csökkentett hosszának nevezzük, hosszával egyenlő egy matematikai inga, amelynek rezgési periódusa megegyezik a fizikaival, azaz.

O 1 pont, amely az O felfüggesztési ponton és a C tömegközépponton át húzott egyenesen fekszik, adott hosszúságú távolságbanl 0 -tól forgástengely, az inga lengésközéppontjának nevezzük (1. ábra). A lengés középpontja mindig a tömegközéppont alatt van. Az O felfüggesztési pont és az O 1 lengésközpont konjugált egymással, azaz. a felfüggesztési pont mozgatása a lengés középpontjába nem változtatja meg az inga lengési periódusát. A felfüggesztési pont és a lengés középpontja megfordítható, ezek közötti távolság a csökkentett hosszl 0 a fizikai inga egyik fajtája, az úgynevezett megfordítható inga.

Jelöljük azzal J 0 az inga tehetetlenségi nyomatéka a tömegközéppontján átmenő tengely körül. Steiner tétele alapján a tehetetlenségi nyomatékJaz elsővel párhuzamos bármely tengelyhez képest:

Ahol m- az inga tömege,l– a tengelyek közötti távolság.

Ekkor, amikor az ingát az O felfüggesztési pontra felfüggesztjük, a lengés periódusa:

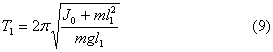
és amikor az O 1 lengőközéppont felfüggeszti, amikor az inga fordított helyzetben van, a periódus:

Ahol l 2 És l 1 – a tömegközéppont és a megfelelő rezgéstengely közötti távolság.

A (9) és (10) egyenletekből:

ahol:

A (11) képlet akkor is érvényben marad, ha az inga két tetszőleges O és O / tengelyhez képest oszcillál, amelyek nem feltétlenül konjugáltak, hanem a mentén helyezkednek el. különböző oldalak az inga tömegközéppontjától.

A működési beállítás és a mérési módszer leírása.

A gravitációs gyorsulás meghatározásához az FP-1 eszközt használjuk (2. ábra),

amely egy 1 fali konzolból áll, amelyre 2 támasztóprizmapárna van felszerelve, és egy fizikai ingából, amely egy homogén 11 fémrúd, amelyre az 5 és 9 lencsék mereven vannak rögzítve és mozdulatlan. A rúd végén elhelyezkedő 5 lencse egy nóniuszos 4 3 skála mentén mozoghat, és egy csavarral 6 rögzíthető a kívánt pozícióban. Az inga a 7 és 10 tartóprizmára függeszthető. A készülék tartalmaz egy speciális állvány az inga tömegközéppontjának helyzetének meghatározásához. Az 5 lencse mozgatásával a 7 és 10 tartóprizmára akasztva az inga lengési periódusainak egyenlősége érhető el, majd az oszcillációs tengelyek konjugálódnak, a tartóprizmák közötti távolság egyenlő lesz a csökkentett hosszúsággal. a fizikai inga.

A gravitációs gyorsulás nagyságát a (11) képlet alapján határozzuk meg. A kísérlet a mennyiségek mérésére irányul T 1 , T 2 , l 1 , l 2 . A (8) képlet a fizikai inga tehetetlenségi nyomatékának meghatározásának kiindulópontja.

Munka előrehaladása

1) A gravitációs gyorsulás meghatározása .

1. Akassza fel az ingát a 7 tartóprizmára, térítse el kis szögben és mérje meg az időt stopperrelt 1 30-50 teljes rezgés. < t 1 > A kísérletet legalább 5-ször megismételjük, és megtaláljuk az átlagos időértéket

2. kiválasztott számú oszcilláció.

Ahol Határozza meg az oszcilláció periódusát:n

3. – az oszcillációk száma. Az inga tömegközéppontjának helyzetének meghatározásához távolítsa el a tartóprizma párnákról, és egyensúlyozza az asztalra szerelt prizma vízszintes szélén, amíg egyenlő. Egyensúly esetén az inga tömegközéppontja a támaszponttal ellentétes rúdban lesz. Anélkül, hogy eltávolítaná az ingát a prizma széléről, mérje meg a távolságot vonalzóvall 1 a 7-es támasz és a tömegközéppont között.

4. Az ingát megfordítva akassza a tartóprizmára 10. Válasszon ki ugyanannyi oszcillációtHatározza meg az oszcilláció periódusát:és ismételje meg a kísérletet legalább 5-ször, keresse meg az oszcilláció periódusát:

Ebben az esetben a T 1 és T 2 periódusok mért értékei legfeljebb 5%-kal térhetnek el egymástól.

5. Távolság keresésel 2 a 10 tartóprizma széle és a tömegközéppont között:l 2 = l 0 – l 1 hol l 0 – a 7 és 10 tartóprizma bordái közötti távolság (ennél az ingánáll 0 =0,730 m).

6. Számítsa ki az átlagértéket < g> a (11) képlet szerint

7. Az eredmény abszolút hibáját a kívánt érték táblázatos értéke alapján becsüljük megg táblázatBratsk szélességi fokára.

8. Keresse meg a relatív hibát.

A mérések és számítások eredményeit az 1. táblázat tartalmazza.

2) E.

1. Fizikai inga tehetetlenségi nyomatékának meghatározásaJHatározza meg a fizikai inga tehetetlenségi nyomatékának átlagos értékét! a (8) képlet szerinti rezgéstengelyhez viszonyítva. A 10 tartóra felfüggesztett inga lengései esetén, T = Tl = l 2 és m 2. Inga tömeg

2. = 10,65 kg. TJ.

3. A közvetett mérések hibáinak számítási módszerével keresse meg az eredmény abszolút hibáját

A mérési és számítási eredmények adatai a 2. táblázatba kerülnek.

T

1. Kérdések a munkavállaláshoz

2. Mi a munka célja?

3. Mi az a fizikai inga? Milyen típusú ingát nevezünk megfordítható ingának? Írja le a fizikai inga rezgési periódusának képletét, és magyarázza el! fizikai jelentése

4. benne foglalt mennyiségek. Milyen feltételek mellett érvényes ez a képlet?

Ismertesse a munkabeállítást és a kísérleti eljárást!

1. Kérdések a munkája védelmében

2. Vezesse le a fizikai inga lengési periódusának képletét!

3. Készítsen differenciálegyenletet a fizikai inga harmonikus rezgéseire, és adja meg a megoldását.

4. Mennyi a fizikai inga csökkentett hossza?

5. Állítsa be Steiner tételét.

Vezesse le a munkaképletet:

a szabadesés gyorsulásának meghatározása;

6. hogy meghatározzuk a fizikai inga tehetetlenségi nyomatékát.TJ/ JKészítsen képletet a relatív hiba kiszámításához a differenciális módszerrel

A fizikai inga olyan merev test, amely képes egy olyan rögzített pont körül oszcillálni, amely nem esik egybe a tehetetlenségi középpontjával. Egyensúlyi helyzetben a C inga tehetetlenségi középpontja az O inga felfüggesztési pontja alatt, ugyanazon a függőlegesen helyezkedik el (50. ábra). Amikor az inga egy α szöggel eltér az egyensúlyi helyzetétől, forgási nyomaték keletkezik, amely az inga egyensúlyi helyzetébe való visszaállítására irányul. Ez a pillanat egyenlő

М = – mglsin(α)

Ahol m az inga tömege, és l– a felfüggesztési pont és az inga tehetetlenségi középpontja közötti távolság. A „–” jel azt jelenti, hogy a forgatónyomaték az ingát egyensúlyi helyzetbe igyekszik visszavinni, azaz a Δα szögváltozással ellentétes irányba irányul. betűvel megjelölve az inga tehetetlenségi nyomatékát a felfüggesztési ponton áthaladó tengelyhez képest J, írhatod:

Bemutatjuk a jelölést:

Ekkor kis eltérések esetén, ha teljesül a sin(α) ≈ α feltétel, megkapjuk a harmonikus rezgések egyenletét:

Az egyensúlyi helyzettől való kis eltérések esetén a fizikai inga harmonikus rezgéseket hajt végre, amelyek ciklikus frekvenciáját a (137) képlet határozza meg. Ennek megfelelően a fizikai inga lengési periódusa egyenlő:

Fizikai inga

A (139) és (134) képletek összehasonlításából az következik, hogy egy matematikai inga, amelynek hossza

ugyanolyan lengésperiódusú lesz, mint az adott fizikai ingának. A mennyiséget (140) a fizikai inga csökkentett hosszának nevezzük. Így a fizikai inga csökkentett hossza egy olyan matematikai inga hossza, amelynek rezgési periódusa egybeesik egy adott fizikai inga periódusával.

A felfüggesztési pontot a tehetetlenségi középponttal összekötő egyenesnek a forgástengelytől kisebb távolságra fekvő pontját fizikai inga lengésközéppontjának nevezzük (lásd az O" pontot az 50. ábrán). ).

Steiner tétele szerint az inga tehetetlenségi nyomatéka l formában lehet bemutatni

J = J 0 + ml 2, (141)

Ahol J 0– a forgástengellyel párhuzamos és az inga tehetetlenségi középpontján átmenő tengely körüli tehetetlenségi nyomaték. Ha a (141)-et behelyettesítjük a (140) képletbe, a következőt kapjuk:

A (142)-ből az következik, hogy a csökkentett hossz mindig nagyobb l, hogy a felfüggesztési pont és a lengés középpontja a tehetetlenségi középpont ellentétes oldalán legyen.

Felfüggesztjük az ingát egy olyan pontban, amely egybeesik a lengés középpontjával O". A (142) szerint a csökkentett hossz ebben az esetben egyenlő lesz

Ahol l"– a lengés kezdeti középpontja és az inga tehetetlenségi középpontja közötti távolság. Ezt figyelembe véve l" = L – l, a (143) kifejezés a következőképpen írható fel:

Mivel J 0 + ml 2 egyenlő az eredeti forgástengely körüli tehetetlenségi nyomatékkal J, és ugyanez az érték a (140) szerint egyenlő a kifejezéssel mlL, akkor a tört számlálója egyenlő lesz nullával. azért L" = L. Ez azt jelenti, hogy amikor az ingát a lengés középpontjában felfüggesztjük, a csökkentett hossz, és így a lengés periódusa ugyanaz lesz, mint az elején. Ebből következően a felfüggesztési pont és a lengőközép kölcsönösségi tulajdonsággal rendelkezik: amikor a felfüggesztési pont átkerül a lengőközéppontba, az előző felfüggesztési pont lesz az új lengésközéppont.

Ezt a pozíciót ún

ROSZHELDOR

Állami oktatási intézmény

"Rosztovszkij állami egyetem kommunikációs eszközök"

(RGUPS)

Fizikai inga tehetetlenségi nyomatékának meghatározása

Útmutató a fizika laboratóriumi munkáihoz

Rostov-on-Don

Ladakin, Yu N.

Fizikai inga tehetetlenségi nyomatékának meghatározása: iránymutatásokat fizika laboratóriumi munkákhoz /,; Magasság. állami Kommunikációs Egyetem. – Rostov n/d, 2007. – 10 p. : ill. – Bibliográfia: 2 cím.

Rövid elméleti információkat tartalmaz az „Oszcillációk” és a „Dinamika” szakaszokról. szilárd" A leírás és a működési elv megadva laboratóriumi telepítés, a munkavégzés menete és az ajánlott irodalom. Megfogalmazva tesztkérdések a megszerzett tudás megszilárdítására.

Az irányelveket az Orosz Állami Pedagógiai Mérnöki Egyetem Fizika Tanszéke jóváhagyta közzétételre. Az Orosz Állami Pedagógiai Egyetem minden szakának hallgatói számára készült.

Lektor: Dr. Phys.-Math. tudományok, prof. (RGUPS)

Oktatási kiadás

A FIZIKAI INGA TETEGETÉSI NYOMATÉKÁNAK MEGHATÁROZÁSA

Útmutató a fizika laboratóriumi munkáihoz

Szerkesztő

Műszaki szerkesztés és lektorálás

Közzétételre aláírva: 07.12.28. 60´84/16 formátum.

Újságpapír. Rizográfia. Feltételes sütő l. 0,58.

Akadémiai szerk. l. 0,53. Példányszám 50 példány. Szerk. 58. sz. rend.

Rosztovi Állami Közlekedési Egyetem.

Rizográfia RGUPS.

Egyetem címe: 344038, Rostov n/D, pl. Rosztovi lövészezred Népi Milícia, 2.

Ó Rostov Állami Közlekedési Egyetem, 2007

Eszközök és tartozékok: Oberbeck inga, teszttest (korong), elektronikus stopper, tolómérő, vonalzó, csavarhúzó.

A munka célja: fizikai inga tehetetlenségi nyomatékának meghatározása kísérleti és számítási módszerekkel Steiner-tétel segítségével.

A tehetetlenségi nyomaték az fizikai mennyiség, amely kvantitatívan jellemzi egy test tehetetlenségi tulajdonságait forgó mozgása során. A merev test forgási tehetetlensége nemcsak magának a testnek a tömegétől függ, hanem ennek a tömegnek a forgástengelyhez viszonyított térbeli eloszlásától is.

A geometriailag szimmetrikus testek tehetetlenségi nyomatéka viszonylag egyszerűen kiszámítható. Testek tehetetlenségi nyomatékának analitikus számítása szabad formában nehézkes feladat, amely számítási tapasztalatot igényel.

A felfüggesztési ponton átmenő tengely körül oszcilláló, tetszőleges alakú szilárd testet (1. ábra) ún. fizikai inga. Meg kell határozni ennek az inga tehetetlenségi nyomatékát.

Egyensúlyi helyzetben tömegközéppont https://pandia.ru/text/80/230/images/image006_43.gif" width="40" height="23">.

Két erő hat az ingára: gravitáció https://pandia.ru/text/80/230/images/image008_41.gif" width="23" height="27"> (feltételezzük, hogy nincsenek súrlódási erők és ellenállás az inga mozgásával szemben. Az ingát a függőlegestől egy szöggel térítsük el ( sarok elfogultság). Az inga magára hagyott további mozgása az ábra síkjára merőleges tengellyel egybeeső tengely körüli forgásnak tekinthető.

Szerint a dinamika alaptörvénye forgó mozgás az inga () tengelyhez viszonyított szöggyorsulása megegyezik az ingára ​​ható összes erő eredő nyomatékának és az azonos tengelyhez viszonyított tehetetlenségi nyomatékának arányával:

. (1)

Az erőnyomatéka hagyományosan nullával egyenlő (ahogy az ábrán látható, ennek az erőnek a karja egyenlő nullával), és ezért a kapott erőnyomaték egyenlő a gravitációs nyomatékkal. a tengely:

, (2)

ahol: a fizikai inga tömege, a szabadesés gyorsulása, https://pandia.ru/text/80/230/images/image003_53.gif" width="20" height="21"> és a tömegközéppont A mínusz jel a (2) képletben azt jelzi, hogy a gravitációs nyomaték megakadályozza a szögeltolódás növekedését.

Kis amplitúdók esetén (https://pandia.ru/text/80/230/images/image017_28.gif" width="79" height="27"> és (1)-ből a (2) figyelembevételével egy Lineáris differenciálegyenlet 2. rend:

, Hol . (3)

Ez azt jelenti, hogy a fizikai inga kis oszcillációi harmonikus Vel körkörös frekvenciaÉs időszak(az időszakra fázis az oszcilláció a következőre változik:

. (4)

A (4) képlet segítségével kísérletileg meghatározhatja bármely test tehetetlenségi nyomatékát a mennyiségek mérésével, és:

. (5)

Fizikai ingát a segítségével lehet előállítani Oberbeck inga. 4 rúdból álló keresztből áll, amely egy mereven rögzített vízszintes tengelyen forgó perselyhez van rögzítve. Ha egy testet, például egy korongot rögzítünk az egyik rúdhoz, akkor a kapott rendszer egy fizikai inga lesz (2. ábra). A kapott inga forgástengelye egybeesik az Oberbeck-inga tömegközéppontjával.

Az (5) képlet közvetlen használata egy adott inga tehetetlenségi nyomatékának kiszámításához nehéz. Ez annak köszönhető, hogy nehéz pontosan meghatározni mind a tömegközéppont helyzetét, mind a teljes inga tömegét.

Alakítsuk át az (5) egyenletet könnyen mérhető paraméterekkel rendelkező formává. Az inga két mereven összekapcsolt test rendszere: kirakva Oberbeck inga tömeggel és homogén korong tömeggel (3. ábra).

Mivel a tömegközépponthoz viszonyítva vektor összege a rendszer testeinek tömegnyomatéka nulla, kapjuk:

.

Ezért a forgástengely és a kapott inga tömegközéppontja közötti távolság egyenlő:

. (6)

Helyettesítsük (6)-ot (5)-be, és ezt figyelembe véve , kapunk egy számítási képletet a vizsgált fizikai inga tehetetlenségi nyomatékának kísérleti meghatározására:

. (7)

A (6) és (7) képletekben #ris3">3. ábra) A korong homogén - tömegközéppontja egybeesik geometriai középpont. A (7) képletben szereplő összes mennyiség most már meglehetősen könnyen mérhető.

Másrészt az inga tehetetlenségi nyomatéka akkor számítható, ha a terheletlen Oberbeck-inga tehetetlenségi nyomatéka ismert (a tengelyhez viszonyítva). Valóban az ingatlan miatt additívitás tehetetlenségi nyomatékunk van:

,

ahol egy sugarú korong tehetetlenségi nyomatéka a Huygens-Steiner-tétel alapján számítva a tengelyhez viszonyítva ():

.

Így az általunk vizsgált inga tehetetlenségi nyomatékának kiszámítására szolgáló képlet a következőképpen alakul:

. (8)

1 Ismert tömegű lemez https://pandia.ru/text/80/230/images/image033_17.gif" width="11 height=23" height="23"> a forgástengely és a lemez a tanártól szerezhető be.

2 Az ingát kis szögben eltérítve gerjesztjük annak rezgéseit. Mérje meg tíz rezgés idejét. Ismételje meg a mérést még 2 alkalommal, és rögzítse az eredményeket a táblázatban.

Oktatási intézmény

Matematika és Fizika Tanszék

INGA

MÓDSZERTANI UTASÍTÁSOK LABORATÓRIUMI MUNKÁHOZ 1.2

fegyelem szerint

"FIZIKA"

Oktatási intézmény

"MAGASÍTOTT ÁLLAMI KOMMUNIKÁCIÓS FŐISKOLA"

Matematika és Fizika Tanszék

EGY FIZIKAI TEhetetlenségi nyomaték MEGHATÁROZÁSA

INGA

MÓDSZERTANI UTASÍTÁSOK LABORATÓRIUMI MUNKÁHOZ 1.2

fegyelem szerint

"FIZIKA"

minden szakos hallgató számára

EGY FIZIKAI TEhetetlenségi nyomaték MEGHATÁROZÁSA

INGA

A MUNKA CÉLJA: fizikai inga tehetetlenségi nyomatékának meghatározása, valamint a tehetetlenségi nyomaték függésének vizsgálata az inga tömegközéppontjának forgástengelyhez viszonyított helyzetétől.

ESZKÖZÖK ÉS TARTOZÉKOK: fizikai inga konzolon, stopper, prizma állványon, mérleg vonalzó.

AZ ELMÉLET ELEMEI

A testnek valamilyen stabil helyzethez (egyensúlyi helyzethez) viszonyított periodikus elmozdulásait ún oszcilláló mozgás vagy egyszerű rezgések. Az oszcillációs mozgások általában összetett fizikai folyamatokat képviselnek. A rezgések tanulmányozása számos alkalmazott tudományág (akusztika, gépelmélet, szeizmológia stb.) alapjául szolgál.

A legegyszerűbb rezgéstípus a harmonikus oszcilláló mozgás. Egy test harmonikus rezgései akkor lépnek fel, ha az elmozdulással arányos erő hat rá, pl. . Ezt az erőt visszaállításnak nevezik. A helyreállító erő jellege eltérő lehet (rugalmas erő, gravitáció stb.) Harmonikus mozgásnál az út függősége (elmozdulás) ) időből szinusz- vagy koszinuszfüggvénnyel kifejezve:

,

Ahol - a test maximális elmozdulása az egyensúlyi helyzetből (amplitúdó),

- körkörös vagy ciklikus frekvencia,

- egy teljes rezgés ideje (periódus),

- az oszcilláció kezdeti fázisa .

A harmonikus rezgéseket végző test gyorsulása arányos az elmozdulással, és mindig az egyensúly felé irányul, azaz. az időeltolódás minden egyes pillanatára és a gyorsulás ellentétes jelei vannak:

. (1)

Harmonikus rezgéseket a gravitáció hatására az ingák hajtanak végre, ha a függőleges helyzettől (egyensúlyi helyzet) való eltérés szögei kicsik. Az ingák lehetnek egyszerűek vagy összetettek. A hosszú menetre felfüggesztett kis testet (anyagpontot), amelynek feszültsége és súlya elhanyagolható, egyszerű ill. matematikai inga. Tetszőleges alakú, vízszintes tengelyre rögzített, a súlyponton át nem haladó szilárd test összetett ill. fizikai inga.

Bármely szilárd test tekinthető tömegekkel állandóan összefüggő anyagi pontok gyűjteményének
,
, . . .,
.

Amikor egy fizikai inga szöggel eltér egyensúlyi helyzetétől (1. ábra) minden elemére hatással lesz a forgástengelyhez viszonyított gravitációs nyomaték . Ezen erők nyomatékainak összege egyenlő az eredő gravitációs erők nyomatékával
, az inga súlypontjára alkalmazva (pont ).

A gravitációs nyomaték hatására az inga szöggyorsulással oszcillálni kezd
.

Ha a forgástengelytől való távolságot jelöljük a súlypontba keresztül , majd a gravitációs pillanat
így lenne kifejezve:

vagy kis szögben

, (2)

Ahol - váll erő
,

- az inga tömege,

- test szabadesésének gyorsulása adott helyen.

Amikor az inga oszcillál, a súlypontja egy körív mentén mozog, ezért Newton második forgási törvényének egyenlete az ingára ​​is alkalmazható. A következő formában lesz írva:

, (3)

Ahol ‑ a test tehetetlenségi nyomatéka a forgástengely körül .

Tehetetlenségi nyomaték anyagi pont tömegszorzatának nevezzük (
)távolság négyzetenként ( ) a forgástengelytől ahhoz (
). Egy test tehetetlenségi nyomatéka egyenlő a részecskéinek ugyanazon tengelyhez viszonyított tehetetlenségi nyomatékainak összegével, azaz

.

Az értéket behelyettesítve a (3) egyenletbe
és a szöggyorsulás tekintetében megoldva azt kapjuk

, (4)

A (4) egyenlet csak abban különbözik az (1) egyenlettől, hogy lineáris mennyiségek helyett szögmennyiségeket tartalmaz.

Az (1) és (4) egyenlet összehasonlításából az következik
vagy
, amelyből megkapjuk a fizikai inga lengési periódusának képletét:

. (5)

A fizikai inga (5) rezgési periódusának képletéből megtaláljuk a tehetetlenségi nyomatékát:

, (6)

Ahol
- az inga lengési periódusa.

Ez a kifejezés egy számítási képlet a fizikai inga tehetetlenségi nyomatékának meghatározására.

KÍSÉRLETI MÓDSZER ÉS A TELEPÍTÉS LEÍRÁSA

Ebben a munkában a fizikai inga egy acélrúdból áll

ОD, amelyre csavarokkal egy masszív hengeres B testet rögzítenek (2. ábra). A tartócsavarok elengedésekor a B test a rúd mentén mozgatható, és ezáltal az inga súlypontjának helyzete megváltoztatható.

Az inga felfüggesztéséhez használjon egy speciális tartót, amelyen az inga a ponton fel van függesztve .

Az inga súlypontjának megtalálása (pont ) egy speciális, stabil állványra szerelt prizma. Ennek a prizmának a peremére vízszintesen helyezzük el az ingát, és az egyensúlyozást figyelve olyan helyzetet találunk, amelyben az inga jobb és bal oldalára ható gravitációs nyomatékok egyenlőek lesznek (3. ábra). Ebben a helyzetben az inga súlypontja a támaszponttal szemben lévő rúdban lesz. Távolság
skála segítségével határozzuk meg.

A MUNKA VÉGREHAJTÁSÁNAK ELJÁRÁSA

stb. Mert , És r 3.

Függőség -tól grafikusan ábrázoljuk a kiválasztott koordinátarendszerben, és az értéket a vízszintes tengelyen ábrázoljuk (m), és a függőlegesen (kg m 2 ).

TESZTKÉRDÉSEK

A fizikai inga definíciója.

Anyagi pont tehetetlenségi nyomatékának és test tehetetlenségi nyomatékának meghatározása.

Adjon meg 2 definíciót az erőnyomatékra (a súlyponttól a forgástengelyig mért távolságon és az erőkaron keresztül)!

Írja fel az inga mozgásának dinamikájának második főtételét, és állítson le egy munkaképletet a fizikai inga lengési periódusára!

Tekerje fel a felfüggesztő menetet az inga tengelye körül és rögzítse.

Ellenőrizze, hogy a gyűrű alsó széle megegyezik-e az oszlopon lévő skála nullával. Ha nem, csavarja le a felső tartót, és állítsa be a magasságát. Csavarja be a felső tartót.

Nyomja meg az ezredmásodperces óra (mobiltelefon) „START” gombját.

Abban a pillanatban, amikor az inga áthalad az alsó ponton, állítsa le az ezredmásodperces órát.

Tekerje fel a felfüggesztő menetet az inga tengelye körül, ügyelve arra, hogy egyenletesen legyen feltekerve, egyik fordulat a másik mellé.

Rögzítse az ingát, ügyelve arra, hogy a szál ebben a helyzetben ne legyen túl csavarodva.

Jegyezze fel az inga esési idejének mért értékét.

Határozza meg az időzítést n= 10-szer.

Határozza meg az inga átlagos esési idejének értékét a következő képlettel:

Ahol n– a végzett mérések száma, t i-ban kapott időérték én- az a fagy, t– az inga esési idejének átlagértéke.

A készülék függőleges oszlopán található skála segítségével határozza meg az inga által az esés során megtett távolságot.

A (11) képlet és ismert átmérőértékek felhasználásával d oÉs d n, határozza meg a tengely átmérőjét a köré tekert cérnával együtt.

A (10) képlet segítségével számítsa ki az inga tömegét a kísérletben felállított gyűrűvel együtt. Rajtuk vannak ábrázolva az egyes elemek tömegértékei.

A (9) képlet segítségével határozza meg az inga tehetetlenségi nyomatékát.

Hasonlítsa össze elméleti értéke tehetetlenségi nyomaték

I elmélet = I o + I m,

Ahol én o– a tengely tehetetlenségi nyomatéka, én m- a lendkerék tehetetlenségi nyomatéka, amelyet a következő képletekkel számítanak ki:

I o = m o r o 2 / 2; I k = m m r m 2 / 2 .

Gyakorlati adatok:

Inga hossza.

1. táblázat.

Mindent behelyettesítve és kiszámolva a következőt kapjuk:

I 1 =(0,00090±0,00001) kg*m2.

Következtetés: A munka során meghatároztuk az inga tehetetlenségi nyomatékait a tekercselt cérna különböző hosszúságaira és meghatároztuk a hibákat. A számított eredmények és a kísérleti érték összehasonlítása jelentős eltérést mutat az adatokban.

Következtetés: Meghatároztuk az inga kísérleti és elméleti tehetetlenségi nyomatékait, amelyek

és összehasonlította őket

1.1. A Maxwell-inga mozgása egy példa egy merev test síkbeli mozgására, amelyben minden pontjának pályája párhuzamos síkok. Ezt a mozgást le lehet redukálni az inga transzlációs mozgására és a tömegközéppontján átmenő tengely körüli forgó mozgásra, amely merőleges ezekre a síkra.

Ez a fajta mozgás elterjedt a technikában: henger gördülése síkon, autó kerekei, közúti autó görgője, forgó helikopter légcsavar mozgatása stb.

1.2. Ennek célja laboratóriumi munka egy merev test síkmozgásának kísérleti ismerkedése a Maxwell-inga példáján és az inga tehetetlenségi nyomatékának meghatározásával.

2. ALAPFOGALMAK

2.1. A Maxwell inga egy kis lendkerék. A gravitáció és az inga tengelyére előre feltekercselt szálak feszítőereje hatására leengedhető (1. ábra). A lefelé irányuló mozgás során a szálak teljesen letekerednek. Az elcsavaratlan lendkerék ugyanabban az irányban tovább forog, és a tengely körül tekeri a szálakat, aminek következtében felemelkedik, miközben lassítja a mozgását. A legfelső pont elérése után újra lefelé kezd.

A lendkerék periodikusan ismétlődő mozgást végez, ezért nevezik ingának. Tehát a Maxwell-inga mozgása két szakaszra osztható: süllyesztésre és felemelkedésre.

2.2. A transzlációs és forgó mozgás dinamikájának alaptörvényei szerint (a megfelelő tengelyekre), figyelmen kívül hagyva a levegővel szembeni súrlódási erőket és a szálak függőlegestől való eltérését, írjuk.

Ahol m- az inga tömege, én- az inga tehetetlenségi nyomatéka a tengelyhez képest, - inga tengely sugara, N- minden menet feszítőereje, g- szabadesés gyorsulás, a- az inga tömegközéppontjának lineáris gyorsulása, - szöggyorsulás. A szálak nyújthatatlansága miatt

Ezek az egyenletek az inga mozgásának első és második szakaszára egyaránt érvényesek. A kezdeti feltételek a különböző szakaszokban eltérőek: az inga leengedésekor tömegközéppontjának kezdeti sebessége nulla, felemelkedésekor pedig nullától eltérő.

2.3 Az (1), (2), (3) egyenletekből következik

(5)

A nulláról egyenletesen gyorsított mozgáshoz az út időtől való függéséből kezdeti sebesség megtalálhatja az inga lineáris gyorsulását

Ahol t- az inga mozgásának ideje a felső ponttól az alsó pontig, h- az ezalatt megtett távolságot. at van ; (7)

Vegye figyelembe, hogy a lineáris gyorsulás és a feszítőerők iránya nem függ attól, hogy az inga felfelé vagy lefelé mozog. Egy teljes rezgés során a lineáris sebesség az alsó pontban az ellenkező irányba változtatja irányát, de a lineáris gyorsulás és az erők nem változnak. A szögsebesség éppen ellenkezőleg, nem változtatja meg az irányát, de az erőnyomaték és a szöggyorsulás az alsó pontban megfordul.

2.4. Felfelé emelkedéskor az inga ugyanolyan lassan mozog. Magasság h2, amelyre felemelkedik, kisebb lesz, mint az, amelyikről leszáll h1. E magasságkülönbség határozza meg a menetek ütközési deformációs erőinek leküzdésére fordított mechanikai energia csökkenését és a mozgással szembeni ellenállást.

Az elveszett mechanikai energia aránya

(9)

TELEPÍTÉSI LEÍRÁS

3.1. A beépítési rajz az ábrán látható. 2. Az 1 alaphoz egy 2 oszlop van rögzítve, amely a 3 felső tartót tartja, amelyen egy 4 elektromágnes, egy 5 fotoelektromos érzékelő és egy 6 gomb található az inga felfüggesztés kiegyenlítésére. Az alsó konzolhoz egy második fotoelektromos érzékelő 7 van rögzítve. A Maxwell lengőkerék egy 9 tengelyre szerelt 8 tárcsából és egy masszív 10 gyűrűből áll, amely a tengelyre felcsavarva van felakasztva. Az ingát egy elektromágnes tartja a felső helyzetben. Az inga süllyesztési és emelési magasságát a készülék oszlopán elhelyezett 11 mm-es vonalzó segítségével határozzuk meg. Az MS 12 ezredmásodperces órát időmérésre tervezték t Maxwell-inga mozgásai. Az időszámlálás kezdete és vége automatikusan megtörténik a fent említett fotóérzékelők segítségével.

A Maxwell-inga tehetetlenségi nyomatékát közvetetten határozzák meg.

A (6) és (8) egyenletekből következik, hogy a tehetetlenségi nyomaték kiszámítható a képlet segítségével

Itt m– az inga teljes tömege,

m = m O+m d+mK , (11)

Ahol m O - tengely tömeg, m d - a lemez tömege.

4. MÉRÉSEK RENDJE

4.1. Műszaki adatok.

4.1.1. Írja be a telepítési adatokat a táblázatba. 1.

1. táblázat

4.1.2. Lépj be a táblázatba. Az ingaelemek tömegének és átmérőjének 2 értéke. Ezek az adatok a telepítésen vannak feltüntetve.

2. táblázat

4.3. Maxwell-inga tehetetlenségi nyomatékának meghatározása.

4.2.2. Tekerje fel a felfüggesztő szálakat az inga tengelyére szimmetrikusan, forgassa el, és rögzítse az ingát. Nagyon óvatosan kell dolgoznia.

4.2.3. Engedje el az ingát, és kezdje el számolni az időt. Állítsa le a visszaszámlálást az alsó pontnál.

4.2.5. Írja be az inga mozgási idejének mért értékét a 3. táblázatba. A 4.2.2. és 4.2.3. szakaszban leírt műveletek megismétlésével mérje meg még 10 alkalommal az időt, és írja be az adatokat a táblázatba. 3.

3. táblázat

4.3. Mechanikai energiaveszteség meghatározása

4.3.1. Használjon vonalzót a magasság meghatározásához h 1, amelyről az inga leszáll; lépj be az asztalba 3.

4.3.2. Ismételje meg a 4.2.2. és 4.2.3. szakaszban leírt műveleteket, hagyja, hogy az inga végezzen öt teljes oszcillációt, és mérje meg a magasságkülönbséget. d h. Végezze el ezt a mérést egyszer, és írja be az eredményt a táblázatba. 3.

5. A MÉRÉSI EREDMÉNYEK FELDOLGOZÁSA

5.1. Maxwell-inga tehetetlenségi nyomatékának meghatározása.

Számítsa ki az inga mozgási idejének átlagos értékét, és írja be a táblázatba! 3.

Számítsa ki az inga mozgási idejének mérésénél az átlagos négyzethibát!

(12)

5.1.3. Számítsa ki az abszolút véletlen hibát

D t sl = 2,1D.S.. (13)

5.1.4. Számítsa ki a teljes abszolút hibát!

D t = D t сл + D t inc.(14)

5.1.5. Számítsa ki a relatív hibát

Helyezze el az összes számított értéket a táblázatban. 3.

5.1.6. A (10) képlet segítségével számítsa ki az inga tehetetlenségi nyomatékát, helyettesítve az átlagos értékét.

5.1.7. Számítsa ki az inga tehetetlenségi nyomatékának relatív hibáját!

, (16)

Ahol D m , D r O, D h1- a megfelelő mennyiségek műszerhibái, Dt – a mozgási idő teljes abszolút hibája; m- az inga teljes tömege, a (11) képlet alapján számítva.

5.1.8. A kapott érték alapján e J kiszámítja az abszolút hibaértéket DJ a tehetetlenségi nyomaték meghatározásában

DJ = e J J= . (17)

Kerek DJ egy jelentős számjegyhez és az értékekhez „J az abszolút hiba szintjére.

5.1.9. A végeredményt írd be az űrlapba!

J = `J± D J =(±) kg × m 2 . (18)

5.2. A mechanikai energiaveszteség meghatározása Maxwell-inga mozgása során.

5.2.1. A (9) képlet a Maxwell-inga öt lengése során elveszett mechanikai energia hányadát fejezi ki; egy oszcilláció esetén a részesedés ötször kisebb lesz:

6. ÁLLÁSVÉDELEM SZÁMÁRA benyújtott KÉRDÉSEK

1. A dinamika alaptörvénye előre mozgás.

3. Hogyan hat az impulzusok és axiális nyomaték Maxwell-inga lendülete mozgásának legalacsonyabb pontján? Magyarázza meg okait.

4. Maxwell-inga összenergia-maradásának törvénye.

5. Keresse meg a lineáris és szögsebesség inga a legalacsonyabb pontján.

6. Merev test tehetetlenségi nyomatéka (definíció). Mitől függ a mérete?

7. Határozza meg a transzlációs mozgás kinetikus energiájának és a forgó mozgás kinetikus energiájának arányát adott Maxwell-inga esetén!

8. Hogyan változnak a lineáris és szöggyorsulások a Maxwell-inga mozgási periódusa alatt?

9. Merev test impulzusa és axiális szögimpulzusa.

10. Becsülje meg a szálak feszességét, amikor az inga áthalad a legalacsonyabb ponton (a benne lévő „ütés” időtartamát egyenlőnek vesszük Dt"0,05c).

11. Hogyan változik az inga mozgási ideje, ha tengelyének sugarát megkétszerezzük?

12. Kinetikus energia merev test transzlációs és forgó mozgása.

13. Sugárú tárcsa tehetetlenségi nyomatékának kiszámítása R, tömeg m

14. Milyen erők és nyomatékok hatnak a Maxwell-ingára ​​mozgása során? Hogyan változnak ezek az időszak alatt?

15. Sugárú gyűrű tehetetlenségi nyomatékának kiszámítása R, tömeg m a síkjára merőleges középponton átmenő tengelyhez képest.

16. Adja meg a (10) képletet a mechanikai energia megmaradásának törvénye alapján! (Kérjük, vegye figyelembe, hogy a Maxwell-ingánál E-től vr >>E postázni).

17. Az inga mozgásának melyik részén, felső vagy alsó részén nagyobb a mechanikai energiaveszteség? Magyarázza meg az okokat.