Nors kompleksinius skaičius sudėti ir atimti patogiau atlikti algebrine forma, daugyba ir dalyba yra lengviau atliekama naudojant trigonometrinę kompleksinių skaičių formą.
Paimkime du savavališkus kompleksinius skaičius, pateiktus trigonometrine forma:
Padauginę šiuos skaičius, gauname:

Bet pagal trigonometrijos formules

![]()
Taigi, dauginant kompleksinius skaičius, dauginami jų moduliai ir argumentai

sulankstyti. Kadangi šiuo atveju moduliai konvertuojami atskirai, o argumentai - atskirai, daugyba trigonometrine forma yra lengviau nei algebrine forma.
Iš lygybės (1) išplaukia šie santykiai:

Kadangi dalyba yra atvirkštinis daugybos veiksmas, tai gauname

Kitaip tariant, dalinio modulis yra lygus dividendo ir daliklio modulių santykiui, o koeficiento argumentas yra skirtumas tarp dividendo ir daliklio argumentų.
Dabar apsistokime geometrine prasme dauginant kompleksinius skaičius. Formulės (1) - (3) rodo, kad norint rasti sandaugą, pirmiausia reikia padidinti skaičiaus modulį nekeičiant jo argumento, o tada padidinti gauto skaičiaus argumentą nekeičiant jo modulio. Pirmoji iš šių operacijų geometriškai reiškia homotetiškumą taško O atžvilgiu su koeficientu , o antroji reiškia pasukimą taško O atžvilgiu kampu, lygiu į Atsižvelgiant į čia vienas veiksnys yra pastovus, o kitas kintamasis, galime suformuluoti rezultatą. taip: formulė
Nors kompleksinius skaičius sudėti ir atimti patogiau atlikti algebrine forma, daugyba ir dalyba yra lengviau atliekama naudojant trigonometrinę kompleksinių skaičių formą.
Paimkime du savavališkus kompleksinius skaičius, pateiktus trigonometrine forma:
Padauginę šiuos skaičius, gauname:

Bet pagal trigonometrijos formules

![]()
Taigi, dauginant kompleksinius skaičius, dauginami jų moduliai ir argumentai

sulankstyti. Kadangi šiuo atveju moduliai konvertuojami atskirai, o argumentai - atskirai, daugyba trigonometrine forma yra lengviau nei algebrine forma.
Iš lygybės (1) išplaukia šie santykiai:

Kadangi dalyba yra atvirkštinis daugybos veiksmas, tai gauname

Kitaip tariant, dalinio modulis yra lygus dividendo ir daliklio modulių santykiui, o koeficiento argumentas yra skirtumas tarp dividendo ir daliklio argumentų.
Dabar panagrinėkime geometrinę kompleksinių skaičių daugybos reikšmę. Formulės (1) - (3) rodo, kad norint rasti sandaugą, pirmiausia reikia padidinti skaičiaus modulį nekeičiant jo argumento, o tada padidinti gauto skaičiaus argumentą nekeičiant jo modulio. Pirmoji iš šių operacijų geometriškai reiškia homotetiškumą taško O atžvilgiu su koeficientu , o antroji reiškia pasukimą taško O atžvilgiu kampu, lygiu į Atsižvelgiant į čia vienas veiksnys yra pastovus, o kitas kintamasis, galime suformuluoti rezultatą. taip: formulė
Sudėtingi skaičiai– tai minimali daugelio mums pažįstamų išplėtimas realūs skaičiai. Esminis jų skirtumas tas, kad atsiranda elementas, kuris kvadratu duoda -1, t.y. aš, arba.
Bet koks kompleksinis skaičius susideda iš dviejų dalių: tikras ir įsivaizduojamas:
Taigi aišku, kad realiųjų skaičių aibė sutampa su kompleksinių skaičių aibe su nuline įsivaizduojamąja dalimi.
Populiariausias kompleksinių skaičių rinkinio modelis yra įprasta plokštuma. Pirmoji kiekvieno taško koordinatė bus jo tikroji dalis, o antroji – įsivaizduojama dalis. Tada pačių kompleksinių skaičių vaidmuo bus vektoriai, kurių pradžia yra taške (0,0).
Operacijos su kompleksiniais skaičiais.
Tiesą sakant, jei atsižvelgsime į kompleksinių skaičių aibės modelį, intuityviai aišku, kad dviejų kompleksinių skaičių sudėjimas (atimtis) ir daugyba atliekami taip pat, kaip ir atitinkamos operacijos su vektoriais. O tai reiškia vektorinis produktas vektoriai, nes šios operacijos rezultatas vėl yra vektorius.
1.1 Papildymas.
(Kaip matote, ši operacija tiksliai atitinka)
1.2 Atimtis, panašiai gaminamas pagal šią taisyklę:
2. Daugyba.
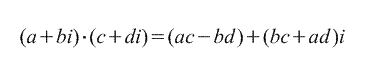
3. Padalinys.
Apibrėžiama tiesiog kaip atvirkštinė daugybos operacija.

Kompleksinio skaičiaus z modulis yra toks dydis:
 ,
,
akivaizdu, kad tai vėlgi yra tik vektoriaus (a, b) modulis (ilgis).
Dažniausiai kompleksinio skaičiaus modulis žymimas kaip ρ.
Pasirodo, kad
z = ρ(cosφ+isinφ).

Tai tiesiogiai išplaukia iš trigonometrinės kompleksinio skaičiaus rašymo formos: formules :

Paskutinė formulė vadinama Moivre'o formulė. Formulė gaunama tiesiogiai iš jos n-oji kompleksinio skaičiaus šaknis:

taigi kompleksinio skaičiaus z yra n-osios šaknys.
Kompleksinis skaičius yra formos skaičius , kur ir yra realieji skaičiai, vadinamieji įsivaizduojamas vienetas. Skambina numeriu tikroji dalis () kompleksinis skaičius, skaičius vadinamas įsivaizduojama dalis () kompleksinis skaičius.
Sudėtiniai skaičiai žymimi sudėtinga plokštuma:

Kaip minėta aukščiau, raidė paprastai žymi realiųjų skaičių rinkinį. Daugelis tas pats kompleksiniai skaičiai dažniausiai žymimas „paryškinta“ arba pastorinta raide. Todėl raidė turėtų būti dedama ant brėžinio, nurodant faktą, kad turime sudėtingą plokštumą.
Algebrinė kompleksinio skaičiaus forma. Kompleksinių skaičių sudėtis, atimtis, daugyba ir dalyba
Kompleksinių skaičių sudėjimas
Norėdami pridėti du kompleksinius skaičius, turite pridėti jų tikrąją ir įsivaizduojamą dalis:
z 1 + z 2 = (a 1 + a 2) + i* (b 1 + b 2).
Kompleksiniams skaičiams galioja pirmosios klasės taisyklė: z 1 + z 2 = z 2 + z 1 – suma nesikeičia perstačius terminus.
Kompleksinių skaičių atėmimas
Veiksmas panašus į pridėjimą, vienintelis ypatumas yra tas, kad poskyrį reikia dėti į skliaustus, o tada skliaustus reikia atidaryti standartiniu būdu, pakeitus ženklą:
z 1 + z 2 = (a 1 – a 2) + i*(b 1 – b 2)
Kompleksinių skaičių dauginimas
Pagrindinė kompleksinių skaičių lygybė:
Kompleksinių skaičių sandauga:
z 1 * z 2 = (a 1 + i*b 1)* (a 2 + i*b 2) = a 1 *a 2 + a 1 *i*b 2 + a 2 *i*b 1 + i 2 *b 1 *b 2 = a 1 *a 2 - b 1 *b 2 +i*(a 1 *b 2 +a 2 *b 1).
Kaip ir suma, kompleksinių skaičių sandauga yra keičiama, tai yra, lygybė yra teisinga: .
Kompleksinių skaičių dalyba
Atliekamas skaičių padalijimas vardiklį ir skaitiklį padauginus iš vardiklio konjuguotos išraiškos.
2 Klausimas. Sudėtinga plokštuma. Kompleksinių skaičių modulis ir argumentai
Kiekvienas kompleksinis skaičius z = a + i*b gali būti susietas su tašku su koordinatėmis (a;b), ir atvirkščiai, kiekvienas taškas su koordinatėmis (c;d) gali būti susietas su kompleksiniu skaičiumi w = c + i* d. Taigi tarp plokštumos taškų ir kompleksinių skaičių aibės nustatomas vienas su vienu atitikimas. Todėl kompleksiniai skaičiai gali būti pavaizduoti kaip taškai plokštumoje. Paprastai vadinama plokštuma, kurioje pavaizduoti kompleksiniai skaičiai sudėtinga plokštuma.

Tačiau dažniau kompleksiniai skaičiai vaizduojami kaip vektorius, kurių pradžia yra taške O, o būtent kompleksinis skaičius z = a + i*b vaizduojamas kaip taško su koordinatėmis (a;b) spindulio vektorius. Tokiu atveju kompleksinių skaičių vaizdas iš ankstesnio pavyzdžio bus toks: 
Dviejų kompleksinių skaičių sumos vaizdas yra vektorius, lygus vektorių, vaizduojančių skaičius ir , sumai. Kitaip tariant, sudėjus kompleksinius skaičius, pridedami ir juos reprezentuojantys vektoriai.

Tegul kompleksinis skaičius z = a + i*b pavaizduotas spindulio vektoriumi. Tada vadinamas šio vektoriaus ilgis modulis skaičius z ir žymimas |z| .
|
|

Kampas, kurį sudaro skaičiaus spindulio vektorius su ašimi, vadinamas argumentas skaičiai ir žymimas arg z. Skaičiaus argumentas nustatomas ne vienareikšmiškai, o kartotinio ribose. Tačiau paprastai argumentas nurodomas diapazone nuo 0 arba diapazone nuo -iki. Be to, skaičius turi neapibrėžtą argumentą.
Naudodami šį ryšį galite rasti kompleksinio skaičiaus argumentą:
Be to, pirmoji formulė galioja, jei skaičiaus vaizdas yra pirmame ar ketvirtame ketvirtyje, o antrasis, jei jis yra antrame ar trečiame. Jei , tai kompleksinis skaičius vaizduojamas vektoriumi Oy ašyje ir jo argumentas lygus /2 arba 3*/2.
Paimkime dar vieną naudingą formulę. Tegul z = a + i*b. Tada,


























