1°

1°. Равенки на тангентата рамнина и нормала за случај на експлицитна дефиниција на површината.

Да разгледаме една од геометриските примени на парцијални изводи на функција од две променливи. Нека функцијата z = f (x ;y)диференцијабилна во точката (x 0; y 0)некоја област ДÎ R 2. Ајде да ја исечеме површината С,претставувајќи ја функцијата z,авиони x = x 0И y = y 0(сл. 11).

Авион X = x 0ја пресекува површината Спо некоја линија z 0 (y),чија равенка се добива со замена во изразот на оригиналната функција z ==f (x ;y)наместо Xброеви x 0 .Точка М 0 (x 0 ;y 0,f (x 0 ;y 0))припаѓа на кривата z 0 (y).Поради диференцијабилната функција zво точката М 0функција z 0 (y)е исто така диференцијабилна во точката y =y 0 .Затоа, во овој момент во авионот x = x 0до кривата z 0 (y)може да се нацрта тангента л 1.

Спроведување слично размислување за делот на = y 0,ајде да изградиме тангента л 2до кривата z 0 (x)во точката X = x 0 -Директно 1 1 И 1 2 дефинираат рамнина наречена тангентна рамнинадо површината Сво точката М 0.

Ајде да ја создадеме нејзината равенка. Бидејќи авионот минува низ точката Мо(x 0 ;y 0 ;z 0),тогаш неговата равенка може да се запише како

A(x - xo) + B(y - yo) + C (z - zo) = 0,

што може да се препише вака:

z -z 0 = A 1 (x – x 0) + B 1 (y – y 0) (1)

(поделете ја равенката со -C и означувате ).

Ќе најдеме А 1и Б 1.

Тангентни равенки 1 1 И 1 2 изгледаат како

соодветно.

Тангента л 1лежи во рамнина a , затоа, координатите на сите точки л 1ја задоволува равенката (1). Овој факт може да се напише во форма на систем

Решавајќи го овој систем во однос на B 1, го добиваме тоа со спроведување слично размислување за тангентата л 3, лесно е да се утврди тоа.

Замена на вредностите А 1и B 1 во равенката (1), ја добиваме саканата равенка на тангентна рамнина:

Линија што минува низ точка М 0и нормално на тангентата рамнина конструирана во оваа точка на површината се нарекува нејзина нормално.

Користејќи го условот за перпендикуларност на права и рамнина, лесно е да се добие канонски равенкинормални:

Коментар.Формулите за тангентата рамнина и нормална на површината се добиваат за обични, т.е., неспецијални точки на површината. Точка М 0површина се нарекува специјални,ако во овој момент сите парцијални изводи се еднакви на нула или барем еден од нив не постои. Ние не ги разгледуваме таквите точки.

Пример. Напиши равенки за тангентата рамнина и нормална на површината во нејзината точка М(2; -1; 1).

Решение. Ајде да ги најдеме парцијалните деривати на оваа функција и нивните вредности во точката М

Оттука, применувајќи ги формулите (2) и (3), ќе имаме: z-1=2(x-2)+2(y+1)или 2х+2у-z-1=0- равенка на тангентна рамнина и - нормални равенки.

2°. Равенки на тангентата рамнина и нормала за случај на имплицитна дефиниција на површината.

Доколку површината Сдадена со равенката F (x ; y;z)= 0, потоа равенките (2) и (3), земајќи го предвид фактот дека парцијалните изводи може да се најдат како изводи на имплицитна функција.

Дефиниција 1 : Тангентата рамнина на површината во дадена точка P (x 0, y 0, z 0) е рамнина што минува низ точката P и ги содржи сите тангенти конструирани во точката P на сите можни криви на оваа површина што минуваат низ точката P.

Нека површината s е дадена со равенката Ф (X, на, z) = 0 и точка П (x 0 , y 0 , з 0) припаѓа на оваа површина. Дозволете ни да избереме некоја крива на површината Л, поминувајќи низ точката Р.

Нека X = X(т), на = на(т), z = z(т) - параметарски равенкилинии Л.

Да претпоставиме дека: 1) функционира Ф(X, на, z) е диференцијабилна во точката Ри не сите негови парцијални деривати во овој момент се еднакви на нула; 2) функции X(т), на(т), z(т) се исто така диференцијабилни.

Бидејќи кривата припаѓа на површината s, координатите на која било точка на оваа крива, заменети во равенката на површината, ќе ја претворат во идентитет. Така, идентичната еднаквост е вистина: Ф [x(т), на(т), z (т)]= 0.

Диференцирање на овој идентитет во однос на променливата т, користејќи го правилото на синџирот, добиваме нова идентична еднаквост, валидна на сите точки на кривата, вклучително и во точката П (x 0 , y 0 , з 0):

Нека точката P одговара на вредноста на параметарот т 0, тоа е x 0 = x (т 0), y 0 = y (т 0), z 0 = z (т 0). Потоа последната релација пресметана во точката Р, ќе ја земе формата

Оваа формула е скаларен производ на два вектори. Првиот е постојан вектор

независно од изборот на кривината на површината.

Вториот вектор е тангентен во точката Рдо линијата Л, што значи дека зависи од изборот на линијата на површината, односно е променлив вектор.

Со воведените ознаки, еднаквоста е:

ајде да препишеме како.

Неговото значење е следново: скаларниот производ е еднаков на нула, затоа, векторите се нормални. Избирање на сите можни кривини кои минуваат низ точка Рна површината s, ќе имаме различни тангентни вектори конструирани во точката Рдо овие линии; векторот не зависи од овој избор и ќе биде нормален на кој било од нив, односно сите тангентни вектори се наоѓаат во иста рамнина, која, по дефиниција, е тангента на површината s, а точката Рво овој случај се нарекува тангентна точка. Векторот е вектор на насока нормален на површината.

Дефиниција 2: Нормалата на површината s во точката P е права линија што минува низ точката P и е нормална на тангентата рамнина конструирана во оваа точка.

Докажавме постоење на тангента рамнина и, следствено, нормална на површината. Да ги запишеме нивните равенки:

Равенка на тангентата рамнина конструирана во точката P (x0, y0, z0) на површината s дадена со равенката F(x, y, z) = 0;

Равенка на нормалата конструирана во точка Рдо површината с.

Пример:Најдете ја равенката на површината формирана со ротација на параболата:

z 2 = 2 стр (y +2)

околу оската y, пресметајте под услов точката М(3, 1, - 3)припаѓа на површината. Најдете ги равенките на нормалната и тангентата рамнина на површината во точката М.

Решение.Користејќи го правилото за пишување површина на ротација, добиваме:

z 2 + x 2 = 2 стр (y +2) .

Заменувајќи ги координатите на точката М во оваа равенка, ја пресметуваме вредноста на параметарот p: 9 + 9 = 2р(1 + 2) . Го снимаме последниот поглед на површината на револуцијата што минува низ точката М:

z 2 + x 2 = 6 (г +2).

Сега ќе ги најдеме равенките на нормалната и тангентата рамнина користејќи ги формулите, за кои прво ги пресметуваме парцијалните изводи на функцијата:

F(x, y) = z 2 + x 2- 6 (г +2):

Тогаш равенката на тангентата рамнина добива форма 6 (x - 3) - 6 (y - 1) - 6 (z + 3) = 0 или x - y - z - 5 = 0;

Да ги разгледаме геометриските примени на изводот на функција од неколку променливи. Нека функција од две променливи е имплицитно одредена: . Оваа функција во својот домен на дефиниција е претставена со одредена површина (Дел 5.1). Да земеме произволна точка на оваа површина , во кој сите три парцијални изводи , , постојат и се континуирани, а барем еден од нив не е еднаков на нула.

Точка со такви карактеристики се нарекува обични површинска точка. Ако барем едно од горенаведените барања не е исполнето, тогаш точката се нарекува посебен површинска точка.

Преку точка избрана на површината, може да се нацртаат многу кривини, од кои секоја може да има тангента.

Дефиниција 5.8.1 . Рамнината во која се наоѓаат сите тангентни линии на линиите на површината што минуваат низ одредена точка се нарекува тангентна рамнина на оваа површина во точката .

Да се ​​троши даден авиондоволно е да има две тангентни линии, односно две кривини на површината. Овие можат да бидат криви добиени како резултат на сечење на дадена површина со рамнини, (сл. 5.8.1).

Дозволете ни да ја напишеме равенката на тангента линија на крива што лежи на пресекот на површината и рамнината. Бидејќи оваа крива лежи во координатниот систем, равенката на тангентата на него во точката, во согласност со став 2.7, има форма:

. (5.8.1)

Според тоа, равенката на тангентата на кривата што лежи на пресекот на површината и рамнината во координатниот систем во истата точка има форма:

. (5.8.2)

Да го користиме изразот за извод на имплицитно одредена функција (Дел 5.7). Потоа, а. Заменувајќи ги овие деривати во (5.8.1) и (5.8.2), добиваме, соодветно:

; (5.8.3)

. (5.8.4)

Бидејќи добиените изрази не се ништо повеќе од равенки на прави линии во канонска форма(точка 15), потоа од (5.8.3) го добиваме векторот на насока , и од (5.8.4) - . Векторски уметнички делаќе даде вектор нормален на дадените тангентни линии и, следствено, на тангентната рамнина:

Следи дека равенката на тангентата рамнина на површината во точката има форма (точка 14):

Дефиниција 5.8.2 . Права линија повлечена низ точка површината нормална на тангентата рамнина во оваа точка се нарекува нормална на површината.

Бидејќи векторот на насоката на нормалата кон површината се совпаѓа со нормалната на тангентата рамнина, нормалната равенка има форма:

.

Скаларно поле

Нека биде одреден регион во просторот, кој зафаќа дел или целиот овој простор. Секоја точка од оваа област, според некој закон, нека биде поврзана со одредена скаларна количина (број).

Дефиниција 5.9.1 . Областа во просторот, чијашто точка е поврзана, според добро познат закон, со одредена скаларна големина, се нарекува скаларно поле..

Ако некој вид координатен систем е поврзан со областа, на пример, правоаголен Декартов систем, тогаш секоја точка добива свои координати. Во овој случај, скаларната големина станува функција на координати: на рамнина – , во тродимензионален простор – . Самата функција која го опишува ова поле често се нарекува скаларно поле. Во зависност од димензијата на просторот, скаларното поле може да биде рамно, тридимензионално итн.

Мора да се нагласи дека големината на скаларното поле зависи само од положбата на точката во регионот, но не зависи од изборот на координатен систем.

Дефиниција 5.9.2 . Скаларното поле кое зависи само од положбата на точка во регионот, но не зависи од времето, се нарекува стационарно..

Нестационарни скаларни полиња, односно временски зависни, нема да се разгледуваат во овој дел.

Примери за скаларни полиња вклучуваат температурно поле, поле на притисок во атмосферата и висинско поле над нивото на океанот.

Геометриски, скаларните полиња често се претставени со користење на таканаречените линии или рамни површини.

Дефиниција 5.9.3 . Множество од сите точки во просторот на кои скаларното поле го има истото значење се нарекува рамна површина или еквипотенцијална површина. Во рамниот случај за скаларно поле, ова множество се нарекува линија на ниво или еквипотенцијална линија.

Очигледно, равенката на површината на ниво ја има формата , линии на ниво – . Со давање на константата во овие равенки различни значења, добиваме семејство на површини или линии на ниво. На пример, (сфери вгнездени една во друга со различни радиуси) или (семејство елипсови).

Примери за нивоа на линии од физиката вклучуваат изотерми (линии со еднакви температури), изобари (линии со еднаков притисок); од геодезија - линии со еднакви висини и сл.

Имено, за тоа што го гледате во насловот. Во суштина, ова е „просторен аналог“ проблеми со наоѓање тангентаИ нормалнина графикот на функција од една променлива, и затоа не треба да се појават тешкотии.

Да почнеме со основните прашања: ШТО Е тангента рамнина и ШТО Е нормална? Многу луѓе ги разбираат овие концепти на ниво на интуиција. Наједноставниот модел што ви паѓа на ум е топка на која лежи тенко рамно парче картон. Картонот се наоѓа што е можно поблиску до сферата и ја допира во една точка. Дополнително, на местото на допир е прицврстено со игла која се држи директно нагоре.

Во теорија, постои прилично генијална дефиниција за тангентна рамнина. Замислете бесплатен површинаи точката што му припаѓа. Очигледно, многу поминува низ поентата просторни линии, кои припаѓаат на оваа површина. Кој какви асоцијации има? =) ...лично замислив октопод. Да претпоставиме дека секоја таква линија има просторна тангентаво точка.

Дефиниција 1: тангентна рамнинадо површината во точка - ова е авион, што содржи тангенти на сите кривини кои припаѓаат на дадена површина и минуваат низ точката.

Дефиниција 2: нормалнодо површината во точка - ова е директно, поминувајќи низ оваа точканормално на тангентата рамнина.

Едноставно и елегантно. Патем, за да не умрете од досада од едноставноста на материјалот, малку подоцна ќе споделам со вас една елегантна тајна што ви овозможува да заборавите на натрупањето различни дефиниции ЕДНАШ ЗА СЕКОГАШ.

Ајде да се запознаеме со работните формули и алгоритмот за решение користејќи конкретен пример. Во огромното мнозинство на проблеми, неопходно е да се конструираат и равенката на тангентната рамнина и нормалната равенка:

Пример 1

Решение:ако површината е дадена со равенката (т.е. имплицитно), тогаш равенката на тангентата рамнина на дадена површина во точка може да се најде со помош на следнава формула:

Посебно внимание посветувам на необични парцијални деривати - нивни не треба да се мешаатСо парцијални деривати на имплицитно одредена функција (иако површината е имплицитно одредена). Кога ги наоѓате овие деривати, треба да се водите од правила за диференцирање на функција од три променливи, односно, кога се разликува во однос на која било променлива, другите две букви се сметаат за константи:

Без да ја напуштиме касата, делумниот дериват го наоѓаме во точката:

Исто така:

Ова беше најнепријатниот момент на одлуката, во кој грешка, ако не е дозволена, тогаш постојано се појавува. Сепак, постои ефективна техникапроверете дали сум зборувал на час Насочен дериват и градиент.

Сите „состојки“ се пронајдени и сега се работи за внимателна замена со дополнителни поедноставувања:

– општа равенкасаканата тангента рамнина.

Силно препорачувам да ја проверите и оваа фаза од решението. Прво треба да бидете сигурни дека координатите на тангентната точка навистина ја задоволуваат пронајдената равенка:

- вистинска еднаквост.

Сега ги „отстрануваме“ коефициентите општа равенкарамнини и проверете ги за совпаѓање или пропорционалност со соодветните вредности. Во овој случај тие се пропорционални. Како што се сеќавате од курс по аналитичка геометрија, - Ова нормален вектортангентна рамнина, а тој е исто така водич векторнормална права линија. Ајде да составиме канонски равенкинормални по вектор на точка и насока:

Во принцип, именителот може да се намали за два, но нема посебна потреба за ова

Одговори:

Не е забрането да се означат равенките со некои букви, но, повторно, зошто? Овде веќе е крајно јасно што е што.

Следниве два примери се за независна одлука. Мал „математички извртувач на јазици“:

Пример 2

Најдете ги равенките на тангентата рамнина и нормалата на површината во точката.

И задача интересна од техничка гледна точка:

Пример 3

Напиши равенки за тангентата рамнина и нормална на површината во точка

Во точката.

Постојат сите шанси не само да се збуните, туку и да наидете на потешкотии при снимањето канонски равенки на правата. И нормалните равенки, како што веројатно разбирате, обично се пишуваат во оваа форма. Иако, поради заборавот или непознавањето на некои нијанси, параметарската форма е повеќе од прифатлива.

Приближни примери за финално извршување на решенија на крајот од часот.

Дали има тангентна рамнина во која било точка на површината? Во принцип, се разбира дека не. Класичниот пример е конусна површина и точка - тангентите во оваа точка директно формираат конусна површина и, се разбира, не лежат во иста рамнина. Лесно е да се потврди дека нешто не е во ред аналитички: .

Друг извор на проблеми е фактот непостоењекој било делумен извод во точка. Сепак, тоа не значи дека во дадена точка не постои единствена тангента рамнина.

Но, тоа беше, повеќе, популарна наука, наместо практично значајна информација, и се враќаме на итните работи:

Како да се напишат равенки за тангента рамнина и нормала во точка,
ако површината е специфицирана со експлицитна функција?

Ајде да го преработиме имплицитно:

И користејќи ги истите принципи наоѓаме делумни деривати:

Така, формулата за тангентна рамнина се трансформира во следнава равенка:

И соодветно, канонските нормални равенки:

Како што може да претпоставите, - овие се веќе „реални“ парцијални изводи на функција од две променлививо точката што ја означувавме со буквата „з“ и беше пронајдена 100500 пати.

Забележете дека во оваа статија доволно е да се запамети првата формула, од која, доколку е потребно, лесно е да се изведе сè друго (се разбира, имајќи основно ниво на обука). Токму овој пристап треба да се користи при изучување на егзактните науки, т.е. од минимум информации мора да се стремиме да „извлечеме“ максимум заклучоци и последици. „Разгледувањето“ и постојното знаење ќе помогнат! Овој принцип е исто така корисен затоа што најверојатно ќе ве спаси во критична ситуација кога знаете многу малку.

Ајде да ги разработиме „модифицираните“ формули со неколку примери:

Пример 4

Напиши равенки за тангентата рамнина и нормална на површината во точка.

Овде има мало преклопување со ознаките - сега буквата означува точка на авионот, но што можете да направите - толку популарна буква...

Решение: да ја составиме равенката на саканата тангента рамнина користејќи ја формулата:

Да ја пресметаме вредноста на функцијата во точката:

Ајде да пресметаме Парцијални деривати од прв редво овој момент:

Така:

внимателно, не брзајте:

Да ги запишеме канонските равенки на нормалата во точката:

Одговори:

И последен пример за сопствено решение:

Пример 5

Запишете ги равенките за тангентата рамнина и нормалата на површината во точката.

Конечно - затоа што ги објаснив буквално сите технички точки и нема ништо посебно да додадам. Дури и самите функции предложени во оваа задача се досадни и монотони - во пракса речиси гарантирано ќе наидете на „полином“, и во оваа смисла, примерот бр. 2 со експонент изгледа како „црна овца“. Патем, многу е поголема веројатноста да се сретне со површина дадена со равенкатаи ова е уште една причина зошто функцијата беше вклучена во статијата како број два.

И, конечно, ветената тајна: па како да избегнете натрупани дефиниции? (Се разбира, не мислам на ситуацијата кога студентот трескавично набива нешто пред испит)

Дефиницијата на кој било поим/феномен/објект, најпрво дава одговор на следното прашање: ШТО Е ТОА? (кој/таков/таков/се). СвесноКога одговарате на ова прашање, треба да се обидете да размислите значајнизнаци, дефинитивноидентификување на одреден концепт/феномен/објект. Да, на почетокот излегува дека е некако непречено, неточно и излишно (наставникот ќе те поправи =)), но со текот на времето се развива сосема пристоен научен говор.

Вежбајте на најапстрактните предмети, на пример, одговорете на прашањето: кој е Чебурашка? Не е толку едноставно ;-) Ова е " лик од бајкитесо големи уши, очи и кафено крзно“? Далеку и многу далеку од дефиниција - никогаш не знаете дека постојат ликови со такви карактеристики... Но, ова е многу поблиску до дефиницијата: „Чебурашка е лик измислен од писателот Едуард Успенски во 1966 година, кој ... (список на главните карактеристични карактеристики)» . Забележете колку добро започна

Преземете од Depositfiles

4. ТЕОРИЈА НА ПОВРШИНИ.

4.1 ПОВРШИНСКИ РАВЕНКИ.

Површина во тридимензионален просторможе да се даде:

1) имплицитно: Ф ( x , y , z ) =0 (4.1)

2) експлицитно: z = ѓ ( x , y ) (4.2)

3) параметарски: (4.3)

или:
(4.3’)

каде се скаларните аргументи
понекогаш наречени криволиниски координати. На пример, сферата
погодно за поставување сферични координати:
.

4.2 ТАНГЕНТА РАМНИНА И НОРМАЛНА НА ПОВРШИНАТА.

Ако правата лежи на површината (4.1), тогаш координатите на нејзините точки ја задоволуваат равенката на површината:

Разликувајќи го овој идентитет, добиваме:

(4.4)

или
(4.4 ’ )

во секоја точка на кривата на површината. Така, векторот на градиент во несингуларни точки на површината (на која функцијата (4.5) е диференцијабилна и
) е нормално на тангентните вектори на која било права на површината, т.е. може да се користи како нормален вектор за да се состави равенката на тангентата рамнина во точката М 0 (x 0 , y 0 , z 0 ) површина

(4.6)

и како вектор на насока во нормалната равенка:

(4.7)

Во случај на експлицитна (4.2) спецификација на површината, равенките на тангентата рамнина и нормалната, соодветно, имаат форма:

(4.8)

И
(4.9)

Со параметарскиот приказ на површината (4.3) векторите
лежат во рамнината на тангентата и равенката на тангентната рамнина може да се запише како:

(4.10)

и нивниот векторски производ може да се земе како нормален вектор на насоката:

а нормалната равенка може да се запише како:

(4.11)

Каде
- вредностите на параметрите што одговараат на точката М 0 .

Во продолжение, ќе се ограничиме на разгледување само на такви површински точки каде што векторите

не е еднаков на нула и не е паралелен.

Пример 4.1 Создадете равенки за тангентата рамнина и нормалата во точката М 0 (1,1,2) до површината на параболоид на револуција
.

Решение: Бидејќи параболоидната равенка е дадена експлицитно, тогаш според (4.8) и (4.9) треба да најдеме
во точката М 0 :

, и во точката М 0
. Тогаш равенката на тангентата рамнина во точката М 0 ќе изгледа вака:

2(x -1)+2(y -1)-(z-2)=0 или 2 x +2 y – з - 2=0, а нормалната равенка
.

Пример 4.2 Составете равенки за тангентата рамнина и нормалата во произволна точка на хеликоидот
, .

Решение. Еве,

Равенка на тангентна рамнина:

или

Нормални равенки:

.

4.3 ПРВА КВАДРАТИЧНА ПОВРШИНА ФОРМА.

Ако површината е дадена со равенката

потоа кривата
може да се даде со равенката
(4.12)

Векторски диференцијал на радиус
долж кривата, што одговара на поместувањето од точката М 0 до најблиската точка М, е еднаква на

(4.13)

Бидејќи
е диференцијалот на лакот на кривата што одговара на истото поместување), тогаш

(4.14)

Каде.

Изразот од десната страна на (4.14) се нарекува прва квадратна форма на површината и игра огромна улога во теоријата на површините.

Јас го интегрирам диференцијалотdsкои се движат од т 0 (одговара на точката М 0 ) до т (одговара на точката М), ја добиваме должината на соодветниот сегмент на кривата

(4.15)

Знаејќи ја првата квадратна форма на површина, можете да ги најдете не само должините, туку и аглите помеѓу кривините.

Ако ду , дв се диференцијали на криволинеарни координати што одговараат на бесконечно мало поместување по една крива, и
- од друга страна, тогаш земајќи ја предвид (4.13):

(4.16)

Користење на формула

(4.17)

првата квадратна форма овозможува да се пресмета површината на регионот
површини.

Пример 4.3 На хеликоид, пронајдете ја должината на спиралата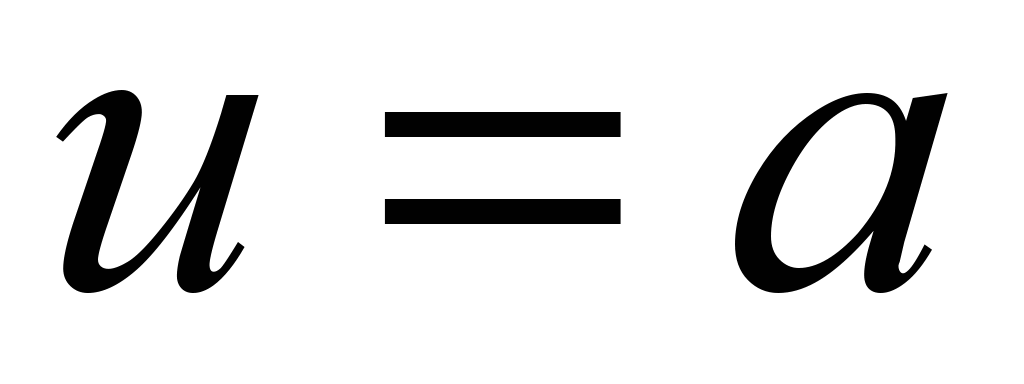
помеѓу две точки.

Решение. Бидејќи на спиралата
, Тоа . Ајде да ја најдеме точката
прва квадратна форма. Имајќи назначено иv = т , ја добиваме равенката на оваа спирална линија во форма . Квадратна форма:

= - прва квадратна форма.

Еве . Во формулата (4.15) во овој случај
и должина на лакот:

=

4.4 ВТОРА КВАДРАТИЧНА ПОВРШИНА ФОРМА.

Да означиме
- единичен вектор нормален на површината
:

(4.18) . (4.23)

Права на површина се нарекува линија на закривеност ако нејзината насока во секоја точка е главната насока.

4.6 ПОИМ НА ГЕОДЕТСКИ ЛИНИИ НА ПОВРШИНА.

Дефиниција 4.1 . Кривата на површината се нарекува геодетска ако нејзината главна нормала во секоја точка каде што кривината е не-нула, таа се совпаѓа со нормалата до површината.

Низ секоја точка на површината во која било насока поминува, и тоа само еден геодетски. На сфера, на пример, големите кругови се геодезика.

Површинската параметаризација се нарекува полугеодетска ако едната фамилија на координатни линии се состои од геодезика, а втората е ортогонална на неа. На пример, на сфера има меридијани (геодезика) и паралели.

Геодезиката на доволно мал сегмент е најкратката меѓу сите кривини блиску до него што ги поврзуваат истите точки.