Комплекс тоонуудыг нэмэх, хасах нь алгебрийн хэлбэрээр хийхэд илүү тохиромжтой байдаг бол үржүүлэх, хуваах нь тригонометрийн нийлмэл тоон хэлбэрийг ашиглан хийхэд хялбар байдаг.
Тригонометрийн хэлбэрээр өгөгдсөн дурын хоёр комплекс тоог авч үзье.
Эдгээр тоог үржүүлснээр бид дараахь зүйлийг авна.

Гэхдээ тригонометрийн томъёоны дагуу

![]()
Тиймээс, нийлмэл тоонуудыг үржүүлэхдээ тэдгээрийн модулиуд, аргументуудыг үржүүлдэг

нугалах. Энэ тохиолдолд модулиудыг тусад нь, аргументуудыг тусад нь хөрвүүлдэг тул тригонометрийн хэлбэрээр үржүүлэх нь алгебрийн хэлбэрээс илүү хялбар байдаг.
Тэгш байдал (1)-ээс дараах харилцаа үүснэ.

Хуваах нь үржүүлэхийн урвуу үйлдэл учраас бид үүнийг олж авдаг

Өөрөөр хэлбэл хуваагчийн модуль нь ногдол ашиг ба хуваагчийн модулиудын харьцаатай тэнцүү байх ба хуваагчийн аргумент нь ногдол ашиг ба хуваагчийн аргументуудын зөрүү юм.
Одоо энэ талаар ярилцъя геометрийн мэдрэмжнийлмэл тоог үржүүлэх. Формула (1) - (3) үржвэрийг олохын тулд эхлээд аргументыг нь өөрчлөхгүйгээр тооны модулийг нэмэгдүүлэх, дараа нь модулийг нь өөрчлөхгүйгээр үүссэн тооны аргументыг нэмэгдүүлэх шаардлагатайг харуулж байна. Эдгээр үйлдлүүдийн эхнийх нь геометрийн хувьд коэффиценттэй О цэгтэй холбоотой гомотетийг, хоёр дахь нь О цэгтэй тэнцүү өнцгөөр эргүүлэхийг хэлнэ Энд нэг хүчин зүйл тогтмол, нөгөө хувьсагч гэж үзвэл үр дүнг томъёолж болно. дараах байдлаар: томъёо
Комплекс тоонуудыг нэмэх, хасах нь алгебрийн хэлбэрээр хийхэд илүү тохиромжтой байдаг бол үржүүлэх, хуваах нь тригонометрийн нийлмэл тоон хэлбэрийг ашиглан хийхэд хялбар байдаг.
Тригонометрийн хэлбэрээр өгөгдсөн дурын хоёр комплекс тоог авч үзье.
Эдгээр тоог үржүүлснээр бид дараахь зүйлийг авна.

Гэхдээ тригонометрийн томъёоны дагуу

![]()
Тиймээс, нийлмэл тоонуудыг үржүүлэхдээ тэдгээрийн модулиуд, аргументуудыг үржүүлдэг

нугалах. Энэ тохиолдолд модулиудыг тусад нь, аргументуудыг тусад нь хөрвүүлдэг тул тригонометрийн хэлбэрээр үржүүлэх нь алгебрийн хэлбэрээс илүү хялбар байдаг.
Тэгш байдал (1)-ээс дараах харилцаа үүснэ.

Хуваах нь үржүүлэхийн урвуу үйлдэл учраас бид үүнийг олж авдаг

Өөрөөр хэлбэл хуваагчийн модуль нь ногдол ашиг ба хуваагчийн модулиудын харьцаатай тэнцүү байх ба хуваагчийн аргумент нь ногдол ашиг ба хуваагчийн аргументуудын зөрүү юм.
Одоо нийлмэл тоог үржүүлэхийн геометрийн утгын талаар ярилцъя. Формула (1) - (3) үржвэрийг олохын тулд эхлээд аргументыг нь өөрчлөхгүйгээр тооны модулийг нэмэгдүүлэх, дараа нь модулийг нь өөрчлөхгүйгээр үүссэн тооны аргументыг нэмэгдүүлэх шаардлагатайг харуулж байна. Эдгээр үйлдлүүдийн эхнийх нь геометрийн хувьд коэффициент бүхий О цэгтэй харьцуулахад ижил төстэй байдлыг илэрхийлдэг бол хоёр дахь нь О цэгтэй тэнцүү өнцгөөр эргэхийг илэрхийлдэг Энд нэг хүчин зүйл тогтмол, нөгөө хувьсагч гэж үзвэл үр дүнг томъёолж болно. дараах байдлаар: томъёо
Нарийн төвөгтэй тоо- Энэ бол бидэнд танил болсон олон зүйлийн хамгийн бага өргөтгөл юм бодит тоо. Тэдний үндсэн ялгаа нь квадрат нь -1 өгдөг элемент гарч ирэх явдал юм. би, эсвэл .
Аливаа комплекс тоо нь хоёр хэсгээс бүрдэнэ. бодит ба төсөөлөл:
Тиймээс бодит тооны олонлог нь тэг төсөөллийн хэсэгтэй нийлмэл тооны олонлогтой давхцаж байгаа нь тодорхой байна.
Комплекс тоонуудын хамгийн алдартай загвар бол энгийн хавтгай юм. Цэг бүрийн эхний координат нь түүний бодит хэсэг, хоёр дахь нь түүний төсөөллийн хэсэг байх болно. Дараа нь цогцолбор тоонуудын үүрэг нь (0,0) цэгээс эхлэлтэй векторууд байх болно.
Комплекс тоон дээрх үйлдлүүд.
Чухамдаа нийлмэл тоонуудын олонлогийн загварыг авч үзвэл хоёр нийлмэл тоог нэмэх (хасах), үржүүлэх нь вектор дээрх харгалзах үйлдлүүдтэй ижил аргаар хийгдэх нь ойлгомжтой юм. Мөн энэ нь гэсэн үг юм вектор бүтээгдэхүүнвекторууд, учир нь энэ үйлдлийн үр дүн нь дахин вектор болно.
1.1 Нэмэлт.
(Таны харж байгаагаар энэ үйлдэл нь яг тохирч байна)
1.2 ХасахҮүний нэгэн адил дараах дүрмийн дагуу үйлдвэрлэнэ.
2. Үржүүлэх.
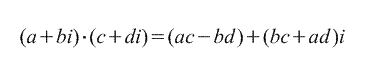
3. Хэлтэс.
Үржүүлэхийн урвуу үйлдэл гэж энгийнээр тодорхойлсон.

z цогцолбор тооны модуль нь дараах хэмжигдэхүүн юм.
 ,
,
Мэдээжийн хэрэг, энэ нь (a,b) векторын зөвхөн модуль (урт) юм.
Ихэнх тохиолдолд комплекс тооны модулийг дараах байдлаар тэмдэглэдэг ρ.
Энэ нь харагдаж байна
z = ρ(cosφ+isinφ).

Комплекс тоог бичих тригонометрийн хэлбэрээс шууд дараах зүйл гарч ирнэ. томъёо :

Сүүлчийн томъёог гэж нэрлэдэг Мойврын томъёо. Томъёо нь үүнээс шууд гардаг нийлмэл тооны n-р үндэс:

иймээс z цогцолбор тооны n-р үндэс байна.
Нарийн нийлмэл тоо гэдэг нь бодит тоо гэж нэрлэгддэг хэлбэр бүхий тоо юм төсөөллийн нэгж. дугаарыг дуудаж байна бодит хэсэг() нийлмэл тоо, тоо гэж нэрлэдэг төсөөллийн хэсэг () нийлмэл тоо.
Цогцолбор тоог дараах байдлаар илэрхийлнэ нарийн төвөгтэй хавтгай:

Дээр дурдсанчлан үсэг нь ихэвчлэн бодит тоонуудын багцыг илэрхийлдэг. Олонэсвэл нийлмэл тооихэвчлэн "том" эсвэл өтгөрүүлсэн үсгээр тэмдэглэдэг. Тиймээс, үсэг нь бидний нарийн төвөгтэй хавтгайтай болохыг харуулсан зураг дээр байрлуулсан байх ёстой.
Комплекс тооны алгебрийн хэлбэр. Комплекс тоог нэмэх, хасах, үржүүлэх, хуваах
Комплекс тоонуудын нэмэх
Хоёр нийлмэл тоог нэмэхийн тулд тэдгээрийн бодит болон төсөөллийн хэсгүүдийг нэмэх хэрэгтэй.
z 1 + z 2 = (a 1 + a 2) + i*(b 1 + b 2).
Комплекс тоонуудын хувьд эхний ангиллын дүрэм хүчинтэй байна: z 1 + z 2 = z 2 + z 1 – нөхцөлүүдийг дахин цэгцлэхээс нийлбэр өөрчлөгдөхгүй.
Цогцолбор тоонуудыг хасах
Үйлдэл нь нэмэхтэй төстэй бөгөөд цорын ганц онцлог нь хасалтыг хаалтанд оруулах шаардлагатай бөгөөд дараа нь хашилтыг тэмдгийн өөрчлөлтөөр стандарт аргаар нээх ёстой.
z 1 + z 2 = (a 1 – a 2) + i*(b 1 – b 2)
Комплекс тоонуудыг үржүүлэх
Комплекс тоонуудын үндсэн тэгш байдал:
Комплекс тоонуудын үржвэр:
z 1 * z 2 = (a 1 + i*b 1)*(a 2 + i*b 2) = a 1 *a 2 + a 1 *i*b 2 + a 2 *i*b 1 + i 2 *b 1 *b 2 = a 1 *a 2 - b 1 *b 2 +i*(a 1 *b 2 +a 2 *b 1).
Нийлбэрийн нэгэн адил нийлбэр тоонуудын үржвэр нь солигддог, өөрөөр хэлбэл тэгш байдал нь үнэн: .
Комплекс тоонуудын хуваагдал
Тоо хуваах ажлыг гүйцэтгэдэг хуваагч болон хуваагчийг хуваагчийн хавсарсан илэрхийллээр үржүүлэх замаар.
2 Асуулт. Нарийн төвөгтэй онгоц. Комплекс тоонуудын модуль ба аргументууд
z = a + i*b нийлмэл тоо бүр нь координаттай (a;b) цэгтэй, харин эсрэгээр (c;d) координаттай цэг бүр w = c + i* цогцолбор тоотой холбоотой байж болно. г. Тиймээс онгоцны цэгүүд болон цогцолбор тоонуудын хооронд нэгээс нэг захидал харилцаа тогтоогддог. Тиймээс комплекс тоонуудыг хавтгай дээрх цэгүүдээр илэрхийлж болно. Комплекс тоонуудыг дүрсэлсэн хавтгайг ихэвчлэн нэрлэдэг нарийн төвөгтэй хавтгай.

Гэсэн хэдий ч ихэвчлэн нийлмэл тоонуудыг О цэгээс эхлэлтэй вектор хэлбэрээр дүрсэлсэн байдаг, тухайлбал z = a + i*b цогцолбор тоог координаттай (a;b) цэгийн радиус вектор хэлбэрээр дүрсэлсэн байдаг. Энэ тохиолдолд өмнөх жишээн дэх комплекс тоонуудын зураг дараах байдалтай байна. 
Хоёр комплекс тооны нийлбэрийн дүрс нь ба тоонуудыг илэрхийлэх векторуудын нийлбэртэй тэнцүү вектор юм. Өөрөөр хэлбэл нийлмэл тоог нэмэхэд тэдгээрийг төлөөлөх векторууд мөн нэмэгддэг.

z = a + i*b комплекс тоог радиус вектороор илэрхийлье. Дараа нь энэ векторын уртыг дуудна модуль z тоо бөгөөд |z|-ээр тэмдэглэнэ .
|
|

Тэнхлэгтэй тооны радиус векторын үүсгэсэн өнцгийг гэнэ маргаантоонуудыг arg z гэж тэмдэглэнэ. Тооны аргументыг дангаар нь биш, харин -ийн үржвэрийн дотор тодорхойлно. Гэсэн хэдий ч, ихэвчлэн аргументыг 0-ээс эсвэл -т хүртэлх мужид зааж өгдөг. Үүнээс гадна тоо нь тодорхойгүй аргументтай.
Энэ хамаарлыг ашиглан та комплекс тооны аргументыг олж болно.
Түүгээр ч зогсохгүй эхний томъёо нь тухайн тооны дүрс нь эхний эсвэл дөрөвдүгээр улиралд, хоёр дахь нь хоёр, гурав дахь хэсэгт байгаа бол хүчинтэй байна. Хэрэв бол нийлмэл тоог Oy тэнхлэг дээрх вектороор илэрхийлэх ба аргумент нь /2 эсвэл 3*/2-тэй тэнцүү байна.
Өөр нэг хэрэгтэй томьёог авч үзье. z = a + i*b гэж үзье. Дараа нь,


























