වීජ ගණිතය හැදෑරීමේ ආරම්භයේදීම ශ්‍රිතයක ප්‍රස්ථාරයක් තැනීමේ කාර්යයට පාසල් සිසුන් මුහුණ දී සිටින අතර ඒවා වසරින් වසර ගොඩනැගීම දිගටම කරගෙන යයි. රේඛීය ශ්‍රිතයක ප්‍රස්ථාරයෙන් පටන් ගෙන, ඔබට කරුණු දෙකක් පමණක් දැන ගැනීමට අවශ්‍ය වන අතර, පරාවලයක් දක්වා, දැනටමත් ලකුණු 6ක්, හයිපර්බෝලා සහ සයින් තරංගයක් අවශ්‍ය වේ. සෑම වසරකම කාර්යයන් වඩ වඩාත් සංකීර්ණ වන අතර ඒවායේ ප්‍රස්ථාර සැකිල්ලක් භාවිතයෙන් තවදුරටත් ගොඩනගා ගත නොහැක, ව්‍යුත්පන්නයන් සහ සීමාවන් භාවිතයෙන් වඩාත් සංකීර්ණ අධ්‍යයනයන් සිදු කිරීම අවශ්‍ය වේ.

ශ්‍රිතයක ප්‍රස්ථාරය සොයා ගන්නේ කෙසේදැයි සොයා බලමු? මෙය සිදු කිරීම සඳහා, අපි සරලම කාර්යයන් සමඟ ආරම්භ කරමු, ඒවායේ ප්‍රස්ථාර ලක්ෂ්‍යයෙන් සටහන කර ඇති අතර පසුව වඩාත් සංකීර්ණ ශ්‍රිතයන් තැනීමේ සැලැස්මක් සලකා බලමු.

රේඛීය ශ්‍රිතයක් රූපගත කිරීම

සරලම ප්‍රස්ථාර තැනීමට, ශ්‍රිත අගයන් සහිත වගුවක් භාවිතා කරන්න. රේඛීය ශ්‍රිතයක ප්‍රස්ථාරය සරල රේඛාවකි. y=4x+5 ශ්‍රිතයේ ප්‍රස්ථාරයේ ලක්ෂ්‍ය සෙවීමට උත්සාහ කරමු.

1. මෙය සිදු කිරීම සඳහා, අපි x විචල්‍යයේ අත්තනෝමතික අගයන් දෙකක් ගෙන, ඒවා එකින් එක ශ්‍රිතයට ආදේශ කර, y විචල්‍යයේ අගය සොයාගෙන සියල්ල වගුවට ඇතුළත් කරමු.
2. x=0 අගය ගෙන එය x - 0 වෙනුවට ශ්‍රිතයට ආදේශ කරන්න. අපට ලැබෙන්නේ: y=4*0+5, එනම් y=5, මෙම අගය 0 යටතේ වගුවේ ලියන්න. එලෙසම, x= ගන්න. 0, අපට y=4*1+5, y=9 ලැබේ.
3. දැන්, ශ්‍රිතයේ ප්‍රස්ථාරයක් තැනීමට, ඔබ මෙම ලක්ෂ්‍ය ඛණ්ඩාංක තලය මත සැලසුම් කළ යුතුය. එවිට ඔබට සරල රේඛාවක් අඳින්න අවශ්යයි.

චතුරස්රාකාර ශ්රිතයක් ප්රස්ථාර කිරීම

චතුර්ශ්‍රිත ශ්‍රිතයක් යනු y=ax 2 +bx +c ආකෘතියේ ශ්‍රිතයකි, මෙහි x යනු විචල්‍යයකි, a,b,c යනු සංඛ්‍යා වේ (a යනු 0 ට සමාන නොවේ). උදාහරණයක් ලෙස: y=x 2, y=x 2 +5, y=(x-3) 2, y=2x 2 +3x+5.

y=x 2 සරලම චතුර් ශ්‍රිතය ගොඩනැගීමට සාමාන්‍යයෙන් ලකුණු 5-7 ක් ගනු ලැබේ. අපි x: -2, -1, 0, 1, 2 විචල්‍ය සඳහා අගයන් ගෙන පළමු ප්‍රස්ථාරය තැනීමේදී මෙන් y හි අගයන් සොයා ගනිමු.

චතුර්ශ්‍රිත ශ්‍රිතයක ප්‍රස්ථාරය පරාවලයක් ලෙස හැඳින්වේ. ශ්‍රිතවල ප්‍රස්ථාර තැනීමෙන් පසු, සිසුන්ට ප්‍රස්ථාරයට අදාළ නව කාර්යයන් ඇත.

උදාහරණය 1: ඕඩිනේට් එක 9 නම් y=x 2 ශ්‍රිතයේ ප්‍රස්ථාර ලක්ෂ්‍යයේ abscissa එක සොයා ගන්න. ගැටලුව විසඳීමට, අපි 9=x 2 ලබා ගන්නවා වෙනුවට එහි අගය 9 ශ්‍රිතයට ආදේශ කළ යුතුයි මෙම සමීකරණය. x=3 සහ x=-3. මෙය ශ්‍රිතයේ ප්‍රස්ථාරයේ ද දැකිය හැක.

කාර්යයක් පර්යේෂණ කිරීම සහ එය සැලසුම් කිරීම

වඩාත් සංකීර්ණ ශ්‍රිතවල ප්‍රස්ථාර සැලසුම් කිරීම සඳහා, ඔබ එය අධ්‍යයනය කිරීම අරමුණු කරගත් පියවර කිහිපයක් සිදු කළ යුතුය. මෙය සිදු කිරීම සඳහා ඔබට අවශ්ය:

1. ශ්‍රිතයේ අර්ථ දැක්වීමේ වසම සොයා ගන්න. අර්ථ දැක්වීමේ වසම යනු x විචල්‍යයට ගත හැකි සියලුම අගයන් වේ. හරය 0 බවට පත්වන හෝ රැඩිකල් ප්‍රකාශනය ඍණ බවට පත්වන එම ලක්ෂ්‍ය නිර්වචන වසමෙන් බැහැර කළ යුතුය.
2. ශ්‍රිතය ඉරට්ටේ ද ඔත්තේ ද යන්න සකසන්න. ඉරට්ටේ ශ්‍රිතයක් යනු f(-x)=f(x) කොන්දේසිය සපුරාලන එකක් බව මතක තබා ගන්න. එහි ප්‍රස්ථාරය Oy සම්බන්ධයෙන් සමමිතික වේ. ශ්‍රිතයක් f(-x)=-f(x) කොන්දේසිය සපුරාලන්නේ නම් ඔත්තේ වේ. මෙම අවස්ථාවෙහිදී, ප්රස්ථාරය සම්භවය පිළිබඳ සමමිතික වේ.
3. ඛණ්ඩාංක අක්ෂ සමඟ ඡේදනය වීමේ ස්ථාන සොයා ගන්න. Ox අක්ෂය සමඟ ඡේදනය වන ලක්ෂ්‍යයේ abscissa සොයා ගැනීම සඳහා, එය f(x) = 0 සමීකරණය විසඳිය යුතුය (ඕඩිනේට් එක 0 ට සමාන වේ). Oy අක්ෂය සමඟ ඡේදනය වන ලක්ෂ්‍යයේ අනුපිළිවෙල සොයා ගැනීමට, x විචල්‍යය වෙනුවට ශ්‍රිතයේ 0 ආදේශ කිරීම අවශ්‍ය වේ (abscissa 0 වේ).
4. කාර්යයේ අසමමිතික සොයා ගන්න. asyptote යනු ප්‍රස්ථාරය දින නියමයක් නොමැතිව ළඟා වන නමුත් කිසි විටෙකත් හරස් නොවන සරල රේඛාවකි. ශ්‍රිතයක ප්‍රස්ථාරයේ අසමමිතිය සොයා ගන්නේ කෙසේදැයි සොයා බලමු.
   • සරල රේඛාවේ සිරස් අසමමිතිය x=a
   • තිරස් අසමමිතිය - සරල රේඛාව y=a
   • ආනත අසමමිතිය - y=kx+b ආකෘතියේ සරල රේඛාව
5. ශ්‍රිතයේ අන්ත ලක්ෂ්‍ය, ශ්‍රිතයේ වැඩිවීමේ සහ අඩුවීමේ කාල අන්තරයන් සොයන්න. ශ්‍රිතයේ අන්ත ලක්ෂ්‍ය සොයා ගනිමු. මෙය සිදු කිරීම සඳහා, ඔබ පළමු ව්‍යුත්පන්නය සොයාගෙන එය 0 ට සමාන කළ යුතුය. ශ්‍රිතය වැඩි වීමේ සිට අඩු වීම දක්වා වෙනස් විය හැක්කේ මෙම ස්ථානවල ය. එක් එක් අන්තරය මත ව්‍යුත්පන්නයේ ලකුණ අපි තීරණය කරමු. ව්‍යුත්පන්නය ධනාත්මක නම්, ශ්‍රිතයේ ප්‍රස්ථාරය සෘණ නම්, එය අඩු වේ.
6. ශ්‍රිත ප්‍රස්ථාරයේ විභේදක ලක්ෂ්‍ය, ඉහළට සහ පහළට උත්තල අන්තරයන් සොයන්න.

විභේදන ලක්ෂ්‍ය සෙවීම වෙන කවරදාටත් වඩා පහසු ය. ඔබට අවශ්‍ය වන්නේ දෙවන ව්‍යුත්පන්නය සොයා ගැනීමයි, පසුව එය ශුන්‍යයට සමාන කරන්න. ඊළඟට අපි එක් එක් අන්තරය මත දෙවන ව්යුත්පන්නයේ සලකුණ සොයා ගනිමු. එය ධනාත්මක නම්, ශ්‍රිතයේ ප්‍රස්ථාරය පහළට උත්තල වේ, එය සෘණ නම්, එය උත්තල වේ.

මෙම ඉගැන්වීම් ද්‍රව්‍ය යොමු කිරීම සඳහා පමණක් වන අතර පුළුල් පරාසයක මාතෘකා වලට සම්බන්ධ වේ. ලිපිය මූලික මූලික ශ්‍රිතවල ප්‍රස්ථාර පිළිබඳ දළ විශ්ලේෂණයක් සපයන අතර වඩාත්ම වැදගත් ගැටළුව ආමන්ත්‍රණය කරයි - ප්‍රස්ථාරයක් නිවැරදිව හා ඉක්මනින් ගොඩනගන්නේ කෙසේද. මූලික ප්‍රාථමික ශ්‍රිතවල ප්‍රස්ථාර පිළිබඳ දැනුමක් නොමැතිව උසස් ගණිතය හැදෑරීමේදී එය අපහසු වනු ඇත, එබැවින් පැරබෝලා, හයිපර්බෝලා, සයින්, කොසයින් යනාදී ප්‍රස්ථාර කෙබඳුදැයි මතක තබා ගැනීම සහ සමහරක් මතක තබා ගැනීම ඉතා වැදගත් වේ. කාර්යයන්හි අර්ථයන්. ප්රධාන කාර්යයන්හි සමහර ගුණාංග ගැනද අපි කතා කරමු.

ද්‍රව්‍යවල සම්පූර්ණත්වය සහ විද්‍යාත්මක පරිපූර්ණත්වය මම ප්‍රකාශ නොකරමි, ප්‍රථමයෙන්, ප්‍රායෝගිකව - එම දේවල් මත අවධාරණය කරනු ලැබේ උසස් ගණිතයේ ඕනෑම මාතෘකාවක් තුළ සෑම පියවරකදීම වචනාර්ථයෙන් මුණගැසෙනවා. ඩමි සඳහා ප්‍රස්ථාර? කෙනෙකුට එහෙම කියන්න පුළුවන්.

පාඨකයන්ගේ නොයෙකුත් ඉල්ලීම් නිසා ක්ලික් කළ හැකි පටුන:

ඊට අමතරව, මාතෘකාව පිළිබඳ අතිශය කෙටි සාරාංශයක් ඇත
- පිටු හයක් අධ්‍යයනය කිරීමෙන් ප්‍රස්ථාර වර්ග 16ක් ප්‍රගුණ කරන්න!

සිරාවටම, හය, මම පවා පුදුම වුණා. මෙම සාරාංශය වැඩිදියුණු කළ ග්‍රැෆික්ස් අඩංගු වන අතර එය නාමික ගාස්තුවකට ලබා ගත හැක. ප්‍රස්ථාර සැමවිටම අත ළඟ ඇති පරිදි ගොනුව මුද්‍රණය කිරීම පහසුය. ව්‍යාපෘතියට සහාය දීම ගැන ස්තුතියි!

සහ අපි වහාම ආරම්භ කරමු:

ඛණ්ඩාංක අක්ෂ නිවැරදිව සාදා ගන්නේ කෙසේද?

ප්‍රායෝගිකව, පරීක්ෂණ සෑම විටම පාහේ සිසුන් විසින් සම්පූර්ණ කරනු ලබන්නේ වෙනම සටහන් පොත්වල, චතුරස්‍රයක පෙළගස්වා ඇත. ඔබට පිරික්සුම් සලකුණු අවශ්ය වන්නේ ඇයි? සියල්ලට පසු, වැඩ, ප්රතිපත්තිමය වශයෙන්, A4 තහඩු මත සිදු කළ හැකිය. කූඩුව අවශ්‍ය වන්නේ චිත්‍රවල උසස් තත්ත්වයේ සහ නිවැරදි සැලසුම සඳහා පමණි.

ශ්‍රිත ප්‍රස්ථාරයක ඕනෑම ඇඳීමක් ආරම්භ වන්නේ ඛණ්ඩාංක අක්ෂයෙනි.

ඇඳීම් ද්විමාන හෝ ත්රිමාණ විය හැක.

අපි මුලින්ම ද්විමාන නඩුව සලකා බලමු කාටිසියානු සෘජුකෝණාස්රාකාර ඛණ්ඩාංක පද්ධතිය:

1) ඛණ්ඩාංක අක්ෂ අඳින්න. අක්ෂය ලෙස හැඳින්වේ x-අක්ෂය , සහ අක්ෂය වේ y-අක්ෂය . අපි සෑම විටම ඒවා ඇඳීමට උත්සාහ කරමු පිළිවෙලට හා වංක නොවේ. ඊතල ද Papa Carlo ගේ රැවුලට සමාන නොවිය යුතුය.

2) අපි "X" සහ "Y" විශාල අකුරු සහිත අක්ෂයන් අත්සන් කරමු. අක්ෂ ලේබල් කිරීමට අමතක නොකරන්න.

3) අක්ෂ දිගේ පරිමාණය සකසන්න: බිංදුවක් සහ දෙකක් අඳින්න. චිත්රයක් සාදන විට, වඩාත් පහසු සහ නිතර භාවිතා කරන පරිමාණය වන්නේ: 1 ඒකකය = 2 සෛල (වම් පැත්තේ ඇඳීම) - හැකි නම්, එයට ඇලී සිටින්න. කෙසේ වෙතත්, වරින් වර එය නෝට්බුක් පත්රය මත ඇඳීම නොගැලපෙන බව සිදු වේ - එවිට අපි පරිමාණය අඩු කරමු: 1 ඒකකය = 1 සෛලය (දකුණු පස ඇඳීම). එය කලාතුරකිනි, නමුත් එය සිදුවන්නේ චිත්‍රයේ පරිමාණය ඊටත් වඩා අඩු කිරීමට (හෝ වැඩි කිරීමට) ය

"මැෂින් තුවක්කුව" අවශ්‍ය නැත ...-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, ....මක්නිසාද යත් ඛණ්ඩාංක තලය ඩෙකාට්ගේ ස්මාරකයක් නොවන අතර ශිෂ්‍යයා පරෙවියෙකු නොවේ. අපි දැම්මා ශුන්යසහ අක්ෂය දිගේ ඒකක දෙකක්. සමහර විට වෙනුවටඒකක, වෙනත් අගයන් "ලකුණු කිරීම" පහසුය, උදාහරණයක් ලෙස, abscissa අක්ෂය මත "දෙකක්" සහ ordinate අක්ෂය මත "තුන" - සහ මෙම පද්ධතිය (0, 2 සහ 3) ද ඛණ්ඩාංක ජාලය අද්විතීය ලෙස අර්ථ දක්වයි.

චිත්රය ඉදිකිරීමට පෙර ඇඳීමේ ඇස්තමේන්තුගත මානයන් තක්සේරු කිරීම වඩා හොඳය. එබැවින්, උදාහරණයක් ලෙස, කාර්යය සඳහා සිරස් සහිත ත්රිකෝණයක් ඇඳීම අවශ්ය නම්, , , 1 ඒකක = 2 සෛලවල ජනප්රිය පරිමාණය ක්රියා නොකරනු ඇති බව සම්පූර්ණයෙන්ම පැහැදිලිය. ඇයි? අපි කාරණය දෙස බලමු - මෙහිදී ඔබට සෙන්ටිමීටර පහළොවක් පහළට මැනිය යුතු අතර, පැහැදිලිවම, ඇඳීම සටහන් පොත් පත්රයකට නොගැලපේ (හෝ යන්තම් නොගැලපේ). එබැවින්, අපි වහාම කුඩා පරිමාණයක් තෝරා ගනිමු: 1 ඒකකය = 1 සෛලය.

මාර්ගය වන විට, සෙන්ටිමීටර සහ නෝට්බුක් සෛල ගැන. නෝට්බුක් සෛල 30 ක සෙන්ටිමීටර 15 ක් අඩංගු බව ඇත්තද? විනෝදය සඳහා, පාලකයෙකු සමඟ ඔබේ සටහන් පොතේ සෙන්ටිමීටර 15 ක් මැනිය. සෝවියට් සමාජවාදී සමූහාණ්ඩුවේ, මෙය සත්ය විය හැකිය ... ඔබ මෙම එකම සෙන්ටිමීටර තිරස් අතට සහ සිරස් අතට මැනියහොත්, ප්රතිඵල (සෛලවල) වෙනස් වනු ඇති බව සැලකිල්ලට ගැනීම සිත්ගන්නා කරුණකි! නිශ්චිතවම කිවහොත්, නවීන නෝට්බුක් පරීක්ෂා කර නැත, නමුත් සෘජුකෝණාස්රාකාර වේ. මෙය විකාරයක් ලෙස පෙනෙන්නට පුළුවන, නමුත් ඇඳීම, උදාහරණයක් ලෙස, එවැනි අවස්ථාවන්හිදී මාලිමා යන්ත්‍රයක් සහිත කවයක් ඉතා අපහසු වේ. ඇත්තම කිව්වොත්, ගෘහස්ථ මෝටර් රථ කර්මාන්තය, වැටෙන ගුවන් යානා හෝ පිපිරෙන බලාගාර ගැන සඳහන් නොකර නිෂ්පාදනයේ හැක් වැඩ සඳහා කඳවුරුවලට යවන ලද ස්ටාලින් සහෝදරයාගේ නිවැරදි භාවය ගැන ඔබ සිතන්නට පටන් ගනී.

ගුණාත්මකභාවය ගැන කතා කිරීම හෝ ලිපි ද්රව්ය පිළිබඳ කෙටි නිර්දේශයක්. අද, විකිණීමට ඇති බොහෝ සටහන් පොත්, අවම වශයෙන් කිවහොත්, සම්පූර්ණ ජරාවකි. ජෙල් පෑන් වලින් පමණක් නොව බෝල්පොයින්ට් පෑන් වලින්ද ඔවුන් තෙත් වන හේතුව නිසා! ඔවුන් කඩදාසි මත මුදල් ඉතිරි කරයි. පරීක්ෂණ සම්පූර්ණ කිරීම සඳහා, එය වඩා මිල අධික වුවද, Arkhangelsk Pulp සහ Paper Mill (ෂීට් 18, හතරැස්) හෝ "Pyaterochka" වෙතින් සටහන් පොත් භාවිතා කිරීම මම නිර්දේශ කරමි. ජෙල් පෑනක් තෝරා ගැනීම යෝග්‍ය වේ, ලාභම චීන ජෙල් නැවත පිරවීම පවා බෝල්පොයින්ට් පෑනකට වඩා හොඳය, එය කඩදාසි මඩ හෝ ඉරා දමයි. මට මතක ඇති එකම "තරඟකාරී" බෝල්පොයින්ට් පෑන Erich Krause ය. ඇය පැහැදිලිව, ලස්සනට සහ ස්ථාවර ලෙස ලියයි - සම්පූර්ණ හරයකින් හෝ පාහේ හිස් එකකින්.

අතිරේකව: විශ්ලේෂණාත්මක ජ්යාමිතියේ ඇස් හරහා සෘජුකෝණාස්රාකාර ඛණ්ඩාංක පද්ධතියක දර්ශනය ලිපියෙහි ආවරණය කර ඇත. දෛශිකවල රේඛීය (නොවන) යැපීම. දෛශික පදනම, සම්බන්ධීකරණ නිල නිවාස පිළිබඳ සවිස්තරාත්මක තොරතුරු පාඩමේ දෙවන ඡේදයෙන් සොයාගත හැකිය රේඛීය අසමානතා.

3D නඩුව

මෙතනත් වාගේ එහෙමයි.

1) ඛණ්ඩාංක අක්ෂ අඳින්න. සම්මත: අක්ෂය අදාළ වේ - ඉහළට යොමු කිරීම, අක්ෂය - දකුණට යොමු කිරීම, අක්ෂය - වමට පහළට යොමු කිරීම දැඩි ලෙසඅංශක 45 ක කෝණයකින්.

2) අක්ෂ ලේබල් කරන්න.

3) අක්ෂය දිගේ පරිමාණය සකසන්න. අක්ෂය දිගේ පරිමාණය අනෙක් අක්ෂයන්හි පරිමාණයට වඩා දෙගුණයක් කුඩා වේ. නිවැරදි ඇඳීමේදී මම අක්ෂය දිගේ සම්මත නොවන "නොච්" භාවිතා කළ බව සලකන්න (මෙම හැකියාව දැනටමත් ඉහත සඳහන් කර ඇත). මගේ දෘෂ්ටි කෝණයෙන්, මෙය වඩාත් නිවැරදි, වේගවත් හා සෞන්දර්යාත්මකව ප්රියජනකයි - අන්වීක්ෂයක් යටතේ සෛලය මැද සොයා බැලීම සහ ඛණ්ඩාංකවල මූලාරම්භයට ආසන්න ඒකකයක් "මූර්ති" කිරීම අවශ්ය නොවේ.

3D චිත්රයක් සාදන විට, නැවතත්, පරිමාණයට ප්රමුඛත්වය දෙන්න
1 ඒකක = සෛල 2 (වමේ ඇඳීම).

මෙම නීති සියල්ල කුමක් සඳහාද? නීති හදන්නේ කඩන්න. ඒක තමයි මම දැන් කරන්නම්. කාරණය නම් ලිපියේ පසුකාලීන ඇඳීම් මා විසින් Excel හි සාදනු ඇති අතර නිවැරදි සැලසුමේ දෘෂ්ටි කෝණයෙන් ඛණ්ඩාංක අක්ෂ වැරදි ලෙස පෙනෙනු ඇත. මට සියලුම ප්‍රස්ථාර අතින් අඳින්න පුළුවන්, නමුත් එක්සෙල් ඒවා වඩාත් නිවැරදිව ඇඳීමට අකමැති බැවින් ඒවා ඇඳීම ඇත්තෙන්ම බියජනක ය.

මූලික ශ්‍රිතවල ප්‍රස්තාර සහ මූලික ගුණාංග

රේඛීය ශ්‍රිතයක් ලබා දෙන්නේ සමීකරණය මගිනි. රේඛීය ශ්‍රිතවල ප්‍රස්ථාරය වේ සෘජු. සරල රේඛාවක් තැනීම සඳහා, කරුණු දෙකක් දැන ගැනීම ප්රමාණවත්ය.

උදාහරණ 1

ශ්‍රිතයේ ප්‍රස්ථාරයක් සාදන්න. අපි කරුණු දෙකක් සොයා ගනිමු. ලකුණු වලින් එකක් ලෙස බිංදුව තෝරා ගැනීම වාසිදායකය.

නම්, එසේ නම්

අපි තවත් කරුණක් ගනිමු, උදාහරණයක් ලෙස, 1.

නම්, එසේ නම්

කාර්යයන් සම්පූර්ණ කරන විට, ලකුණු වල ඛණ්ඩාංක සාමාන්යයෙන් වගුවක සාරාංශ කර ඇත:

තවද අගයන් වාචිකව හෝ කෙටුම්පතක්, කැල්කියුලේටරයක් ​​මත ගණනය කරනු ලැබේ.

කරුණු දෙකක් සොයාගෙන ඇත, අපි ඇඳීම කරමු:

චිත්රයක් සකස් කරන විට, අපි සෑම විටම ග්රැෆික්ස් අත්සන් කරමු.

රේඛීය ශ්‍රිතයක විශේෂ අවස්ථා සිහිපත් කිරීම ප්‍රයෝජනවත් වනු ඇත:

මම අත්සන් තැබූ ආකාරය බලන්න, චිත්‍රය අධ්‍යයනය කිරීමේදී අත්සන් නොගැලපීම් වලට ඉඩ නොදිය යුතුය. මෙම අවස්ථාවේ දී, රේඛා ඡේදනය වන ස්ථානයට යාබදව හෝ ප්‍රස්ථාර අතර පහළ දකුණේ අත්සනක් තැබීම අතිශයින්ම නුසුදුසු ය.

1) පෝරමයේ රේඛීය ශ්‍රිතයක් () සෘජු සමානුපාතිකත්වය ලෙස හැඳින්වේ. උදාහරණ වශයෙන්, . සෘජු සමානුපාතික ප්‍රස්ථාරයක් සෑම විටම සම්භවය හරහා ගමන් කරයි. මේ අනුව, සරල රේඛාවක් තැනීම සරල කර ඇත - එය එක් ලක්ෂයක් සොයා ගැනීමට ප්රමාණවත් වේ.

2) පෝරමයේ සමීකරණයක් අක්ෂයට සමාන්තරව සරල රේඛාවක් නියම කරයි, විශේෂයෙන්, අක්ෂයම සමීකරණයෙන් ලබා දෙයි. ශ්‍රිතයේ ප්‍රස්ථාරය කිසිදු ලක්ෂ්‍යයක් සොයා නොගෙන වහාම ගොඩනගා ඇත. එනම්, ප්‍රවේශය පහත පරිදි තේරුම් ගත යුතුය: "x හි ඕනෑම අගයක් සඳහා y සැමවිටම -4 ට සමාන වේ."

3) පෝරමයේ සමීකරණයක් අක්ෂයට සමාන්තරව සරල රේඛාවක් නියම කරයි, විශේෂයෙන්, අක්ෂයම සමීකරණයෙන් ලබා දෙයි. ශ්‍රිතයේ ප්‍රස්ථාරය ද වහාම සැලසුම් කර ඇත. ඇතුළත් කිරීම පහත පරිදි තේරුම් ගත යුතුය: "x සෑම විටම, y හි ඕනෑම අගයක් සඳහා, 1 ට සමාන වේ."

සමහරු අහයි, ඇයි 6 පන්තිය මතකද?! එය එසේ ය, සමහර විට එය එසේ විය හැකිය, නමුත් වසර ගණනාවක පුහුණුවීම් කාලය තුළ මට ප්‍රස්ථාරයක් සෑදීමේ කාර්යයෙන් ව්‍යාකූල වූ හොඳ සිසුන් දුසිමක් හමු වී ඇත.

චිත්ර ඇඳීමේදී සරල රේඛාවක් තැනීම වඩාත් පොදු ක්රියාවකි.

විශ්ලේෂණාත්මක ජ්‍යාමිතිය තුළ සරල රේඛාව විස්තරාත්මකව සාකච්ඡා කර ඇති අතර උනන්දුවක් දක්වන අයට ලිපිය වෙත යොමු විය හැකිය ගුවන් යානයක සරල රේඛාවක සමීකරණය.

චතුරස්‍ර, ඝන ශ්‍රිතයක ප්‍රස්ථාරය, බහුපදයක ප්‍රස්ථාරය

පැරබෝලා. චතුරස්රාකාර ශ්රිතයක ප්රස්ථාරය () පරාවලයක් නියෝජනය කරයි. සුප්රසිද්ධ නඩුව සලකා බලන්න:

කාර්යයේ සමහර ගුණාංග සිහිපත් කරමු.

ඉතින්, අපගේ සමීකරණයට විසඳුම: - පැරබෝලාවේ ශීර්ෂය පිහිටා ඇත්තේ මෙම අවස්ථාවේදීය. මෙය එසේ වන්නේ මන්දැයි ව්‍යුත්පන්නය පිළිබඳ න්‍යායාත්මක ලිපියෙන් සහ ශ්‍රිතයේ අන්තය පිළිබඳ පාඩමෙන් සොයාගත හැකිය. මේ අතරතුර, අපි අනුරූප "Y" අගය ගණනය කරමු:

මේ අනුව, ශීර්ෂය ලක්ෂ්යයේ වේ

පැරබෝලා සමමිතිය නිර්ලජ්ජිතව භාවිතා කරන අතරේ දැන් අපි වෙනත් කරුණු සොයා ගනිමු. කාර්යය බව සටහන් කළ යුතුය – පවා නොවේ, නමුත්, කෙසේ වෙතත්, කිසිවෙක් පරාවලයේ සමමිතිය අවලංගු කළේ නැත.

ඉතිරි කරුණු සොයා ගන්නේ කුමන අනුපිළිවෙලකටද, අවසාන වගුවෙන් එය පැහැදිලි වනු ඇතැයි මම සිතමි:

මෙම ඉදිකිරීම් ඇල්ගොරිතම සංකේතාත්මකව "ෂටලයක්" හෝ Anfisa Chekhova සමග "ආපසු සහ පසුපසට" මූලධර්මය ලෙස හැඳින්විය හැක.

අපි ඇඳීම සකස් කරමු:

පරීක්ෂා කරන ලද ප්‍රස්ථාර වලින්, තවත් ප්‍රයෝජනවත් අංගයක් මතකයට එයි:

චතුරස්රාකාර කාර්යයක් සඳහා () පහත සඳහන් දේ සත්‍ය වේ.

නම්, පැරබෝලා වල අතු ඉහළට යොමු කෙරේ.

නම්, පැරබෝලාවේ අතු පහළට යොමු කෙරේ.

වක්‍රය ගැන ගැඹුරු දැනුමක් Hyperbola සහ parabola පාඩමෙන් ලබාගත හැක.

ශ්‍රිතය මගින් cubic parabola ලබා දෙනු ලැබේ. මෙන්න පාසලේ සිට හුරුපුරුදු චිත්රයක්:

අපි කාර්යයේ ප්රධාන ගුණාංග ලැයිස්තුගත කරමු

ශ්‍රිතයක ප්‍රස්තාරය

එය පරාවලයක එක් ශාඛාවක් නියෝජනය කරයි. අපි ඇඳීම සකස් කරමු:

කාර්යයේ ප්රධාන ගුණාංග:

මෙම අවස්ථාවේ දී, අක්ෂය වේ සිරස් අසමමිතිය හි හයිපර්බෝලා ප්‍රස්ථාරය සඳහා.

චිත්‍රයක් අඳින විට, ඔබ නොසැලකිලිමත් ලෙස ප්‍රස්තාරය අසමමිතියකින් ඡේදනය වීමට ඉඩ දෙන්නේ නම් එය දළ වැරැද්දකි.

එසේම ඒකපාර්ශ්වික සීමාවන් අපට පවසන්නේ හයිපර්බෝලා බවයි ඉහළින් සීමා නොවේසහ පහතින් සීමා නොවේ.

අපි අනන්තයේ ශ්‍රිතය පරීක්ෂා කරමු: , එනම්, අපි අක්ෂය දිගේ වමට (හෝ දකුණට) අනන්තයට ගමන් කිරීමට පටන් ගන්නේ නම්, “ක්‍රීඩා” ක්‍රමානුකූල පියවරක පවතිනු ඇත. අසීමිත සමීපශුන්යයට ළඟා වන අතර, ඒ අනුව, හයිපර්බෝලාවේ ශාඛා අසීමිත සමීපඅක්ෂයට පිවිසෙන්න.

එබැවින් අක්ෂය වේ තිරස් අසමමිතිය ශ්‍රිතයක ප්‍රස්ථාරය සඳහා, “x” අනන්තය එකතු කිරීමට හෝ අඩු කිරීමට නැඹුරු වේ නම්.

කාර්යය වේ අමුතු, සහ, එබැවින්, හයිපර්බෝලා සම්භවය පිළිබඳ සමමිතික වේ. මෙම කරුණ චිත්‍රයෙන් පැහැදිලි වේ, ඊට අමතරව, එය පහසුවෙන් විශ්ලේෂණාත්මකව සත්‍යාපනය කළ හැකිය: .

පෝරමයේ ශ්‍රිතයක ප්‍රස්ථාරය () හයිපර්බෝලා ශාඛා දෙකක් නියෝජනය කරයි.

නම්, හයිපර්බෝලා පළමු සහ තෙවන ඛණ්ඩාංක කාර්තු වල පිහිටා ඇත(ඉහළ පින්තූරය බලන්න).

නම්, හයිපර්බෝලා දෙවන හා සිව්වන ඛණ්ඩාංක කාර්තු වල පිහිටා ඇත.

ප්‍රස්ථාරවල ජ්‍යාමිතික පරිවර්තනයේ දෘෂ්ටි කෝණයෙන් හයිපර්බෝලා පදිංචියේ සඳහන් රටාව විශ්ලේෂණය කිරීම පහසුය.

උදාහරණය 3

හයිපර්බෝලාවේ දකුණු ශාඛාව සාදන්න

අපි ලක්ෂ්‍යමය ඉදිකිරීම් ක්‍රමය භාවිතා කරන අතර, ඒවා සමස්තයකින් බෙදිය හැකි පරිදි අගයන් තෝරා ගැනීම වාසිදායක වේ:

අපි ඇඳීම සකස් කරමු:

හයිපර්බෝලාවේ වම් ශාඛාව තැනීම අපහසු නොවනු ඇත; දළ වශයෙන් කිවහොත්, ලක්ෂ්‍යමය ඉදිකිරීමේ වගුවේ, අපි එක් එක් සංඛ්‍යාවට මානසිකව අඩුවක් එකතු කර, අනුරූප ලකුණු දමා දෙවන ශාඛාව අඳින්නෙමු.

සලකා බැලූ රේඛාව පිළිබඳ සවිස්තරාත්මක ජ්යාමිතික තොරතුරු Hyperbola සහ parabola ලිපියෙන් සොයාගත හැකිය.

ඝාතීය ශ්‍රිතයක ප්‍රස්තාරය

මෙම කොටසේදී, මම වහාම ඝාතීය ශ්‍රිතය සලකා බලමි, මන්ද යත් 95% ක්ම උසස් ගණිතයේ ගැටළු වලදී එය ඝාතීය වන බැවිනි.

මෙය අතාර්කික සංඛ්‍යාවක් බව මම ඔබට මතක් කරමි: , ප්‍රස්ථාරයක් තැනීමේදී මෙය අවශ්‍ය වනු ඇත, ඇත්ත වශයෙන්ම, මම උත්සවයකින් තොරව ගොඩනඟමි. බොහෝ විට කරුණු තුනක් ප්රමාණවත්ය:

අපි දැනට ශ්‍රිතයේ ප්‍රස්ථාරය පමණක් තබමු, පසුව ඒ ගැන වැඩි විස්තර.

කාර්යයේ ප්රධාන ගුණාංග:

ක්‍රියාකාරී ප්‍රස්ථාර ආදිය මූලික වශයෙන් සමාන වේ.

දෙවන අවස්ථාව ප්‍රායෝගිකව අඩුවෙන් සිදුවන බව පැවසිය යුතුය, නමුත් එය සිදු වේ, එබැවින් එය මෙම ලිපියට ඇතුළත් කිරීම අවශ්‍ය යැයි මම සැලකුවෙමි.

ලඝුගණක ශ්‍රිතයක ප්‍රස්තාරය

ස්වභාවික ලඝුගණකයක් සහිත ශ්රිතයක් සලකා බලන්න.
ලක්ෂ්‍යයෙන් ලක්ෂ්‍ය ඇඳීමක් කරමු:

ලඝුගණකයක් යනු කුමක්දැයි ඔබට අමතක වී ඇත්නම්, කරුණාකර ඔබගේ පාසල් පෙළපොත් වෙත යොමුවන්න.

කාර්යයේ ප්රධාන ගුණාංග:

අර්ථ දැක්වීමේ වසම:

අගයන් පරාසය:.

කාර්යය ඉහත සිට සීමා නොවේ: , සෙමින් වුවද, නමුත් ලඝුගණකයේ ශාඛාව අනන්තය දක්වා ඉහළ යයි.
දකුණු පස ශුන්‍යයට ආසන්න ශ්‍රිතයේ හැසිරීම අපි විමසා බලමු: . එබැවින් අක්ෂය වේ සිරස් අසමමිතිය "x" ලෙස ශ්‍රිතයක ප්‍රස්ථාරය දකුණේ සිට ශුන්‍යයට නැඹුරු වේ.

ලඝුගණකයේ සාමාන්‍ය අගය දැන ගැනීම සහ මතක තබා ගැනීම අත්‍යවශ්‍ය වේ: .

ප්‍රතිපත්තිමය වශයෙන්, පාදයට ලඝුගණකයේ ප්‍රස්ථාරය එකම ලෙස පෙනේ: , , (10 පාදයට දශම ලඝුගණකය) ආදිය. එපමණක් නොව, පාදම විශාල වන තරමට ප්‍රස්ථාරය පැතලි වනු ඇත.

අපි නඩුව සලකා බලන්නේ නැත, මම එවැනි පදනමක් සහිත ප්‍රස්ථාරයක් ගොඩනඟා ඇති අවසාන අවස්ථාව මට මතක නැත. උසස් ගණිතයේ ගැටළු වලදී ලඝුගණකය ඉතා දුර්ලභ ආගන්තුකයක් බව පෙනේ.

මෙම ඡේදය අවසානයේ මම තවත් එක් කරුණක් කියමි. ඝාතීය ශ්‍රිතය සහ ලඝුගණක ශ්‍රිතය- මේවා අන්‍යෝන්‍ය වශයෙන් ප්‍රතිලෝම ශ්‍රිත දෙකකි. ඔබ ලඝුගණකයේ ප්‍රස්ථාරය දෙස සමීපව බැලුවහොත්, මෙය එකම ඝාතකයක් බව ඔබට පෙනෙනු ඇත, එය ටිකක් වෙනස් ලෙස පිහිටා ඇත.

ත්‍රිකෝණමිතික ශ්‍රිතවල ප්‍රස්තාර

ත්‍රිකෝණමිතික වධහිංසා පාසලේදී ආරම්භ වන්නේ කොතැනින්ද? හරි. සයින් සිට

අපි කාර්යය සැලසුම් කරමු

මෙම රේඛාව ලෙස හැඳින්වේ sinusoid.

“pi” යනු අතාර්කික සංඛ්‍යාවක් බව මම ඔබට මතක් කර දෙන්නම්: , සහ ත්‍රිකෝණමිතියේදී එය ඔබේ ඇස් අන්ධ කරයි.

කාර්යයේ ප්රධාන ගුණාංග:

මෙම කාර්යය වේ ආවර්තිතාකාල සීමාව සමඟ. එයින් අදහස් කරන්නේ කුමක් ද? අපි කොටස දෙස බලමු. එහි වමට සහ දකුණට, හරියටම ප්‍රස්ථාරයේ එකම කොටස නිමක් නැතිව පුනරාවර්තනය වේ.

අර්ථ දැක්වීමේ වසම: , එනම් "x" හි ඕනෑම අගයක් සඳහා සයින් අගයක් ඇත.

අගයන් පරාසය:. කාර්යය වේ සීමිතයි: , එනම්, සියලුම "ක්රීඩකයන්" කොටසෙහි දැඩි ලෙස වාඩි වී සිටිති.
මෙය සිදු නොවේ: හෝ, වඩාත් නිවැරදිව, එය සිදු වේ, නමුත් මෙම සමීකරණවලට විසඳුමක් නොමැත.

දැනුම මූලික මූලික කාර්යයන්, ඒවායේ ගුණාංග සහ ප්රස්තාරගුණ කිරීමේ වගු දැන ගැනීමට වඩා අඩු වැදගත්කමක් නැත. ඔවුන් අත්තිවාරම වැනි ය, සියල්ල ඔවුන් මත පදනම් වේ, සියල්ල ඔවුන්ගෙන් ගොඩනගා ඇති අතර සෑම දෙයක්ම ඔවුන් වෙත පැමිණේ.

මෙම ලිපියෙන් අපි සියලුම ප්‍රධාන මූලික කාර්යයන් ලැයිස්තුගත කර, ඒවායේ ප්‍රස්ථාර ලබා දී නිගමනය හෝ සාක්ෂි නොමැතිව ලබා දෙන්නෙමු. මූලික මූලික කාර්යයන්හි ගුණාංගයෝජනා ක්රමය අනුව:

• නිර්වචනයේ වසමේ මායිම්වල ශ්‍රිතයක හැසිරීම, සිරස් අසමමිතිය (අවශ්‍ය නම්, ශ්‍රිතයක අක්‍රමිකතා ලක්ෂ්‍යවල ලිපි වර්ගීකරණය බලන්න);
• ඉරට්ටේ සහ ඔත්තේ;
• උත්තල (උත්තල ඉහළට) සහ අවතල (උත්තල පහළට), විවර්තන ලක්ෂ්‍ය (අවශ්‍ය නම්, ලිපියේ උත්තල ශ්‍රිතයක උත්තල, උත්තල දිශාව, විවර්තන ලක්ෂ්‍ය, උත්තල සහ අපගමනය යන කොන්දේසි බලන්න);
• ආනත සහ තිරස් අසමමිතිය;
• ශ්රිතවල ඒකීය ලක්ෂ්ය;
• සමහර ශ්‍රිතවල විශේෂ ගුණ (උදාහරණයක් ලෙස, ත්‍රිකෝණමිතික ශ්‍රිතවල කුඩාම ධන කාල පරිච්ඡේදය).

ඔබ උනන්දුවක් දක්වන්නේ නම් හෝ, ඔබට න්‍යායේ මෙම කොටස් වෙත යා හැකිය.

මූලික මූලික කාර්යයන්එනම්: නියත ශ්‍රිතය (ස්ථාවර), n වන මූලය, බල ශ්‍රිතය, ඝාතීය, ලඝුගණක ශ්‍රිතය, ත්‍රිකෝණමිතික සහ ප්‍රතිලෝම ත්‍රිකෝණමිතික ශ්‍රිත.

පිටු සංචලනය.

ස්ථිර කාර්යය.

නියත ශ්‍රිතයක් සියලු තාත්වික සංඛ්‍යා කට්ටලය මත සූත්‍රය මගින් නිර්වචනය කරනු ලැබේ, එහිදී C යනු යම් තාත්වික සංඛ්‍යාවක් වේ. නියත ශ්‍රිතයක් x ස්වාධීන විචල්‍යයේ සෑම තථ්‍ය අගයක්ම යැපෙන විචල්‍යයේ y - අගය C සමඟ සම්බන්ධ කරයි. නියත ශ්‍රිතයක් නියතයක් ලෙසද හැඳින්වේ.

නියත ශ්‍රිතයක ප්‍රස්ථාරය x-අක්ෂයට සමාන්තරව සරල රේඛාවක් වන අතර ඛණ්ඩාංක (0,C) සමඟ ලක්ෂ්‍යය හරහා ගමන් කරයි. උදාහරණයක් ලෙස, y=5, y=-2 සහ පහත රූපයේ පිළිවෙලින් කළු, රතු සහ නිල් රේඛා වලට අනුරූප වන නියත ශ්‍රිතවල ප්‍රස්ථාර පෙන්වමු.

නියත ශ්‍රිතයක ගුණ.

• වසම: සම්පූර්ණ තාත්වික සංඛ්‍යා සමූහය.
• නියත කාර්යය ඒකාකාර වේ.
• අගයන් පරාසය: ඒකීය අංකය C වලින් සමන්විත කට්ටලයක්.
• නියත ශ්‍රිතයක් යනු වැඩි නොවන සහ අඩු නොවන (එය නියත වන්නේ එබැවිනි).
• නියතයක උත්තල සහ concavity ගැන කතා කිරීම තේරුමක් නැත.
• රෝග ලක්ෂණ නොමැත.
• ශ්‍රිතය ඛණ්ඩාංක තලයේ ලක්ෂ්‍යය (0,C) හරහා ගමන් කරයි.

Nවන උපාධියේ මූලය.

n යනු එකකට වඩා වැඩි ස්වභාවික සංඛ්‍යාවක් වන සූත්‍රයෙන් ලබා දෙන මූලික මූලික ශ්‍රිතය සලකා බලමු.

n වන උපාධියේ මූලය, n යනු ඉරට්ටේ අංකයකි.

මූල ඝාතීය n හි ඉරට්ටේ අගයන් සඳහා n වන මූල ශ්‍රිතයෙන් පටන් ගනිමු.

උදාහරණයක් ලෙස, ශ්‍රිත ප්‍රස්ථාරවල රූප සහිත පින්තූරයක් මෙන්න සහ , ඒවා කළු, රතු සහ නිල් රේඛා වලට අනුරූප වේ.

ඉරට්ටේ මූල ශ්‍රිතවල ප්‍රස්ථාර ඝාතකයේ අනෙකුත් අගයන් සඳහා සමාන පෙනුමක් ඇත.

ඉරට්ටේ n සඳහා nth root ශ්‍රිතයේ ගුණ.

n වන උපාධියේ මූලය, n යනු ඔත්තේ සංඛ්‍යාවකි.

n ඔත්තේ මූල ඝාතකයක් සහිත n වන මූල ශ්‍රිතය තාත්වික සංඛ්‍යාවල සම්පූර්ණ කට්ටලය මත අර්ථ දක්වා ඇත. උදාහරණයක් ලෙස, මෙහි ශ්‍රිත ප්‍රස්ථාර වේ සහ , ඒවා කළු, රතු සහ නිල් වක්‍ර වලට අනුරූප වේ.

මූල ඝාතකයේ වෙනත් ඔත්තේ අගයන් සඳහා, ශ්‍රිත ප්‍රස්ථාරවලට සමාන පෙනුමක් ඇත.

ඔත්තේ n සඳහා nth root ශ්‍රිතයේ ගුණ.

බල කාර්යය.

බල ශ්‍රිතය ලබා දෙන්නේ පෝරමයේ සූත්‍රයක් මගිනි.

බල ශ්‍රිතයක ප්‍රස්ථාරවල ස්වරූපය සහ ඝාතකයේ අගය අනුව බල ශ්‍රිතයක ගුණ සලකා බලමු.

අපි පූර්ණ සංඛ්‍යා ඝාතක a සමඟ බල ශ්‍රිතයකින් පටන් ගනිමු. මෙම අවස්ථාවෙහිදී, බල ශ්‍රිතවල ප්‍රස්ථාර වර්ගය සහ ශ්‍රිතවල ගුණයන් ඝාතකයේ ඒකාකාර බව හෝ අපූර්වත්වය මෙන්ම එහි ලකුණ මත රඳා පවතී. එබැවින්, අපි පළමුව a හි ඔත්තේ ධන අගයන් සඳහා බල ශ්‍රිත සලකා බලමු, පසුව ධන ඝාතකයන් සඳහා ඉරට්ටේ, පසුව ඔත්තේ සෘණ ඝාතක සඳහා සහ අවසාන වශයෙන්, ඉරට්ටේ සෘණ a සඳහා.

භාගික සහ අතාර්කික ඝාතක සහිත බල ශ්‍රිතවල ගුණ (මෙන්ම එවැනි බල ශ්‍රිතවල ප්‍රස්ථාර වර්ගය) ඝාතකයේ අගය මත රඳා පවතී a. අපි ඒවා සලකා බලමු, පළමුව, ශුන්‍යයේ සිට එක දක්වා, දෙවනුව, එකකට වඩා වැඩි සඳහා, තෙවනුව, සෘණ එක සිට බිංදුව දක්වා, හතරවනුව, සෘණ එකකට වඩා අඩු සඳහා.

මෙම කොටස අවසානයේ, සම්පූර්ණත්වය සඳහා, අපි ශුන්‍ය ඝාතකයක් සහිත බල ශ්‍රිතයක් විස්තර කරමු.

ඔත්තේ ධන ඝාතකයක් සහිත බල ක්‍රියාකාරිත්වය.

ඔත්තේ ධන ඝාතකයක් සහිත බල ශ්‍රිතයක්, එනම් a = 1,3,5,.... සමඟ සලකා බලමු.

පහත රූපයේ දැක්වෙන්නේ බල ක්‍රියාකාරිත්වයේ ප්‍රස්ථාර - කළු රේඛාව, - නිල් රේඛාව, - රතු රේඛාව, - කොළ රේඛාව. a=1 සඳහා අප සතුව ඇත රේඛීය ශ්රිතය y=x.

ඔත්තේ ධන ඝාතකයක් සහිත බල ශ්‍රිතයක ගුණ.

ඒකාකාර ධන ඝාතන සමග බල ක්‍රියාකාරිත්වය.

ඉරට්ටේ ධන ඝාතකයක් සහිත බල ශ්‍රිතයක් සලකා බලමු, එනම් a = 2,4,6,....

උදාහරණයක් ලෙස, අපි බල ශ්‍රිතවල ප්‍රස්ථාර ලබා දෙන්නෙමු - කළු රේඛාව, - නිල් රේඛාව, - රතු රේඛාව. a=2 සඳහා අපට චතුරස්‍ර ශ්‍රිතයක් ඇත, එහි ප්‍රස්ථාරය වේ quadratic parabola.

ඒකාකාර ධන ඝාතකයක් සහිත බල ශ්‍රිතයක ගුණ.

ඔත්තේ සෘණ ඝාතීය සමග බල ශ්‍රිතය.

ඝාතකයේ ඔත්තේ සෘණ අගයන් සඳහා බල ශ්‍රිතයේ ප්‍රස්ථාර බලන්න, එනම් a = -1, -3, -5,....

රූපයේ දැක්වෙන්නේ බල ක්‍රියාකාරිත්වයේ ප්‍රස්ථාර උදාහරණ ලෙස පෙන්වයි - කළු රේඛාව, - නිල් රේඛාව, - රතු රේඛාව, - කොළ රේඛාව. a=-1 සඳහා අප සතුව ඇත ප්රතිලෝම සමානුපාතිකත්වය, කාගේ ප්‍රස්ථාරය අධිබලය.

ඔත්තේ සෘණ ඝාතකයක් සහිත බල ශ්‍රිතයක ගුණ.

සෘණ ඝාතීය පවා සමඟ බල ක්‍රියාකාරිත්වය.

අපි a=-2,-4,-6,.... හි බල ශ්‍රිතය වෙත යමු.

රූපය බල ශ්‍රිතවල ප්‍රස්ථාර පෙන්වයි - කළු රේඛාව, - නිල් රේඛාව, - රතු රේඛාව.

ඒකාකාර සෘණ ඝාතකයක් සහිත බල ශ්‍රිතයක ගුණ.

අගය ශුන්‍යයට වඩා වැඩි සහ එකකට වඩා අඩු තාර්කික හෝ අතාර්කික ඝාතකයක් සහිත බල ශ්‍රිතයක්.

අවදානය යොමු කරන්න! a යනු ඔත්තේ හරයක් සහිත ධන භාගයක් නම්, සමහර කතුවරුන් බල ශ්‍රිතයේ අර්ථ දැක්වීමේ වසම අන්තරය ලෙස සලකයි. ඝාතක a යනු ප්‍රතිවර්තනය කළ නොහැකි භාගයක් බව නියම කර ඇත. දැන් වීජ ගණිතය සහ විශ්ලේෂණ මූලධර්ම පිළිබඳ බොහෝ පෙළපොත්වල කතුවරුන් තර්කයේ සෘණ අගයන් සඳහා ඔත්තේ හරයක් සහිත භාගයක ස්වරූපයෙන් ඝාතකයක් සමඟ බල ක්‍රියාකාරිත්වය නිර්වචනය නොකරයි. අපි හරියටම මෙම මතයට අනුගත වන්නෙමු, එනම්, භාගික ධනාත්මක ඝාතකයන් සහිත බල ශ්‍රිතයන් නිර්වචනය කිරීමේ වසම් ලෙස අපි සලකා බලමු. එකඟ නොවීම් වළක්වා ගැනීම සඳහා මෙම සියුම් කරුණ පිළිබඳ ඔබේ ගුරුවරයාගේ මතය සිසුන්ට සොයා ගැනීමට අපි නිර්දේශ කරමු.

අපි තාර්කික හෝ අතාර්කික ඝාතකයක් සහිත බල ශ්‍රිතයක් සලකා බලමු a, සහ .

අපි a=11/12 (කළු රේඛාව), a=5/7 (රතු රේඛාව), (නිල් රේඛාව), a=2/5 (හරිත රේඛාව) සඳහා බල ශ්‍රිතවල ප්‍රස්ථාර ඉදිරිපත් කරමු.

එකකට වඩා වැඩි නිඛිල නොවන තාර්කික හෝ අතාර්කික ඝාතකයක් සහිත බල ශ්‍රිතයක්.

නිඛිල නොවන තාර්කික හෝ අතාර්කික ඝාතකයක් සහිත බල ශ්‍රිතයක් සලකා බලමු a, සහ .

සූත්‍ර මගින් ලබා දෙන බල ශ්‍රිතවල ප්‍රස්ථාර අපි ඉදිරිපත් කරමු (පිළිවෙලින් කළු, රතු, නිල් සහ කොළ රේඛා).

>

ඝාතීය a හි අනෙකුත් අගයන් සඳහා, ශ්‍රිතයේ ප්‍රස්ථාර සමාන පෙනුමක් ඇත.

බලයේ ක්‍රියාකාරිත්වයේ ගුණ.

සෘණ එකකට වඩා වැඩි සහ ශුන්‍යයට වඩා අඩු සැබෑ ඝාතකයක් සහිත බල ශ්‍රිතයක්.

අවදානය යොමු කරන්න! a යනු ඔත්තේ හරයක් සහිත සෘණ භාගයක් නම්, සමහර කතුවරුන් බල ශ්‍රිතයක අර්ථ දැක්වීමේ වසම විරාමය ලෙස සලකයි. . ඝාතක a යනු ප්‍රතිවර්තනය කළ නොහැකි භාගයක් බව නියම කර ඇත. දැන් වීජ ගණිතය සහ විශ්ලේෂණ මූලධර්ම පිළිබඳ බොහෝ පෙළපොත්වල කතුවරුන් තර්කයේ සෘණ අගයන් සඳහා ඔත්තේ හරයක් සහිත භාගයක ස්වරූපයෙන් ඝාතකයක් සමඟ බල ක්‍රියාකාරිත්වය නිර්වචනය නොකරයි. අපි හරියටම මෙම දර්ශනයට අනුගත වන්නෙමු, එනම්, භාගික භාගික සෘණ ඝාතක සහිත බල ශ්‍රිතයන් නිර්වචනය කිරීමේ වසම් පිළිවෙලින් කට්ටලයක් ලෙස සලකමු. එකඟ නොවීම් වළක්වා ගැනීම සඳහා මෙම සියුම් කරුණ පිළිබඳ ඔබේ ගුරුවරයාගේ මතය සිසුන්ට සොයා ගැනීමට අපි නිර්දේශ කරමු.

අපි බල ශ්‍රිතය, kgod වෙත යමු.

සඳහා බල ශ්‍රිතවල ප්‍රස්ථාරවල ස්වරූපය පිළිබඳ හොඳ අදහසක් ලබා ගැනීමට, අපි ශ්‍රිතවල ප්‍රස්ථාර සඳහා උදාහරණ දෙන්නෙමු. (පිළිවෙලින් කළු, රතු, නිල් සහ කොළ වක්‍ර).

ඝාතීය a, සමඟ බල ශ්‍රිතයක ගුණ.

සෘණ එකකට වඩා අඩු නිඛිල නොවන තාත්වික ඝාතකයක් සහිත බල ශ්‍රිතයක්.

සඳහා බල ශ්‍රිතවල ප්‍රස්ථාර සඳහා උදාහරණ දෙන්නෙමු , ඒවා පිළිවෙලින් කළු, රතු, නිල් සහ කොළ රේඛා මගින් නිරූපණය කෙරේ.

ඍණ එකකට වඩා අඩු පූර්ණ නොවන සෘණ ඝාතකයක් සහිත බල ශ්‍රිතයක ගුණ.

a = 0 විට, අපට ශ්‍රිතයක් ඇත - මෙය ලක්ෂ්‍යය (0;1) බැහැර කර ඇති සරල රේඛාවකි (0 0 ප්‍රකාශනයට කිසිදු වැදගත්කමක් නොදැක්වීමට එකඟ විය).

ඝාතීය ශ්‍රිතය.

ප්‍රධාන මූලික ශ්‍රිතයක් වන්නේ ඝාතීය ශ්‍රිතයයි.

ඝාතීය ශ්‍රිතයේ ප්‍රස්ථාරය, a පාදයේ අගය මත පදනම්ව විවිධ ස්වරූප ගන්නා තැන. අපි මෙය තේරුම් ගනිමු.

පළමුව, ඝාතීය ශ්‍රිතයේ පාදය ශුන්‍යයේ සිට එක දක්වා අගයක් ගන්නා විට, එනම්, .

උදාහරණයක් ලෙස, අපි a = 1/2 - නිල් රේඛාව, a = 5/6 - රතු රේඛාව සඳහා ඝාතීය ශ්‍රිතයේ ප්‍රස්ථාර ඉදිරිපත් කරමු. ඝාතීය ශ්‍රිතයේ ප්‍රස්ථාර පරතරයේ සිට පාදයේ අනෙකුත් අගයන් සඳහා සමාන පෙනුමක් ඇත.

එකකට වඩා අඩු පාදයක් සහිත ඝාතීය ශ්‍රිතයක ගුණ.

ඝාතීය ශ්‍රිතයේ පාදය එකකට වඩා වැඩි වූ විට අපි නඩුව වෙත යමු, එනම්, .

නිදර්ශනයක් ලෙස, අපි ඝාතීය ශ්‍රිතවල ප්‍රස්ථාර ඉදිරිපත් කරමු - නිල් රේඛාව සහ - රතු රේඛාව. එකකට වඩා වැඩි පාදයේ අනෙකුත් අගයන් සඳහා, ඝාතීය ශ්‍රිතයේ ප්‍රස්ථාර සමාන පෙනුමක් ඇත.

එකකට වඩා වැඩි පාදයක් සහිත ඝාතීය ශ්‍රිතයක ගුණ.

ලඝුගණක ශ්‍රිතය.

මීළඟ මූලික මූලික ශ්‍රිතය වන්නේ ලඝුගණක ශ්‍රිතයයි, එහිදී , . ලඝුගණක ශ්‍රිතය අර්ථ දක්වා ඇත්තේ තර්කයේ ධනාත්මක අගයන් සඳහා පමණි, එනම් සඳහා .

ලඝුගණක ශ්‍රිතයක ප්‍රස්ථාරය a පාදයේ අගය අනුව විවිධ ස්වරූප ගනී.

බල කාර්යය. මෙය කාර්යය වේ: y = axn, කොහෙද a, n- ස්ථිර. දී n= 1 අපට ලැබේ සෘජු සමානුපාතිකත්වය: y = පොරව; n = 2 - දී ; n = - 1 - ප්රතිලෝම සමානුපාතිකත්වයහතරැස් පැරබෝලා හෝ. අතිශයෝක්තිය මේ අනුව, මෙම ශ්රිතයන් බල ශ්රිතයේ විශේෂ අවස්ථා වේ. ශුන්‍යය හැර වෙනත් ඕනෑම සංඛ්‍යාවක ශුන්‍ය බලය සමාන බව අපි දනිමු 1, එබැවින්, දී n= 0 බල ශ්‍රිතය නියත අගයක් බවට පත් වේ: = y a , i.e. ඇගේ කාලසටහනඅක්ෂයට සමාන්තරව සරල රේඛාවX, සම්භවය හැර (කරුණාකර පැහැදිලි කරන්න y= 1 ) ඇයි ? ) මෙම සියලු අවස්ථා (සමඟ (nරූපය 13 හි පෙන්වා ඇත 0) සහ රූපය 14 ( < 0). Отрицательные значения nx මෙහි සලකා බලනු නොලැබේ, එබැවින්

සමහර කාර්යයන් මෙන්: 0) සහ රූපය 14 (නම්- පූර්ණ සංඛ්‍යාව, බල ශ්‍රිතයන් විට පවා අර්ථවත් කරයි< 0, но их графики имеют различный вид в зависимости от того, является ли 0) සහ රූපය 14 (xඉරට්ටේ හෝ ඔත්තේ අංකය. nරූප සටහන 15 එවැනි බල කාර්යයන් දෙකක් පෙන්වයි: n = 3.


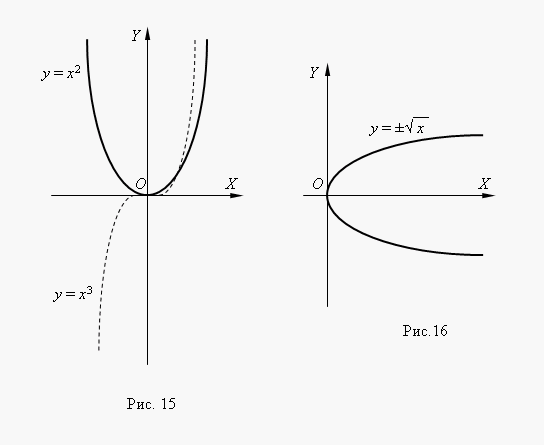
සඳහා n= = 2 සහදී 2 ශ්‍රිතය ඉරට්ටේ සහ එහි ප්‍රස්ථාරය සමමිතික වේ. අක්ෂයට සාපේක්ෂව 0) සහ රූපය 14 (වයි දීy = n 3 = 3 ශ්‍රිතය ඔත්තේ වන අතර එහි ප්‍රස්ථාරය සම්භවයට සාපේක්ෂව සමමිතික වේ ඛණ්ඩාංක කාර්යය.

16 රූපයේ දැක්වෙන්නේ කාර්යයයි. මේ කාර්යය වේ = 0 බල ශ්‍රිතය නියත අගයක් බවට පත් වේ: = n 2 හතරැස් පැරබෝලාවකට ප්‍රතිලෝම. , එහි ප්‍රස්ථාරය 1 වන ඛණ්ඩාංක කෝණයේ ද්වි අංශය වටා හතරැස් පරාවලයක ප්‍රස්ථාරය කරකැවීමෙන් ලබා ගනී.

මෙය ඕනෑම ප්‍රතිලෝම ශ්‍රිතයක ප්‍රස්ථාරය එහි මුල් ශ්‍රිතයේ ප්‍රස්ථාරයෙන් ලබා ගැනීමේ ක්‍රමයකි. මෙය අගයන් දෙකක ශ්‍රිතයක් බව ප්‍රස්ථාරයෙන් අපට පෙනේ (මෙය වර්ගමූලයට ඉදිරියෙන් ඇති ± ලකුණින් ද දැක්වේ). එවැනි ශ්‍රිත ප්‍රාථමික ගණිතයේ අධ්‍යයනය නොකෙරේ, එබැවින් ශ්‍රිතයක් ලෙස අපි සාමාන්‍යයෙන් එහි එක් ශාඛාවක් සලකා බලමු: ඉහළ හෝ පහළ.

තලයේ නියත වශයෙන්ම ඕනෑම ලක්ෂයක ඛණ්ඩාංකය තීරණය වන්නේ එහි ප්‍රමාණ දෙකෙනි: abscissa අක්ෂය සහ ordinate අක්ෂය දිගේ. එවැනි බොහෝ ලක්ෂ්‍යවල එකතුව ශ්‍රිතයේ ප්‍රස්ථාරය නියෝජනය කරයි. X අගය වෙනස් වීම අනුව Y අගය වෙනස් වන ආකාරය එයින් ඔබට දැක ගත හැක.

• උපදෙස්
• එහි ප්‍රස්ථාරය සරල රේඛාවක් නම් ශ්‍රිතයක් ගැන ඔබට කුමක් කිව හැකිද? මෙම රේඛාව ඛණ්ඩාංක මූල ලක්ෂ්‍යය හරහා ගමන් කරන්නේ දැයි බලන්න (එනම්, X සහ Y අගයන් 0 ට සමාන වන එක). එය සමත් වුවහොත්, එවැනි ශ්රිතයක් y = kx සමීකරණය මගින් විස්තර කෙරේ. k හි අගය විශාල වන තරමට මෙම සරල රේඛාව පිහිටා ඇති අක්ෂයට ආසන්න බව තේරුම් ගැනීම පහසුය. Y අක්ෂය ඇත්ත වශයෙන්ම k හි අසීමිත විශාල අගයකට අනුරූප වේ.
• කාර්යයේ දිශාව බලන්න. එය “පහළ වමේ සිට ඉහළ දකුණට” ගියහොත්, එනම්, 3 වන සහ 1 වන ඛණ්ඩාංක කාර්තු හරහා, එය වැඩි වෙමින් පවතී, නමුත් එය “ඉහළ වමේ සිට පහළට දකුණට” (2 වන සහ 4 වන කාර්තු හරහා) යන්නේ නම්, එය අඩු වෙනවා.
• රේඛාවක් මූලාරම්භය හරහා නොයන විට, එය y = kx + b සමීකරණයෙන් විස්තර කෙරේ. ඍජු රේඛාව y = b යන ස්ථානයේ දී y-අක්ෂය ඡේදනය වන අතර, y හි අගය ධන හෝ ඍණ විය හැක.
• n යනු ඔත්තේ සංඛ්‍යාවක් නම්, මෙම ශ්‍රිතයේ ප්‍රස්ථාරය ඝන පරාලයක් වේ. වක්‍රය 1 වන සහ 3 වන ඛණ්ඩාංක කාර්තු වල පිහිටා ඇත, Y අක්ෂය ගැන සමමිතික වන අතර ඛණ්ඩාංකවල මූලාරම්භය හරහා මෙන්ම ලකුණු (-1;-1), (1;1) හරහා ගමන් කරයි. චතුර්ශ්‍රිත ශ්‍රිතය y = ax^2 + bx + c සමීකරණය වන විට, පරාවලයේ හැඩය සරලම අවස්ථාවෙහි (y = x^2) සමාන වේ, නමුත් එහි ශීර්ෂය මූලාරම්භයේ නොමැත.
• ශ්‍රිතයක් y = k/x සමීකරණයෙන් විස්තර කරන්නේ නම් එය හයිපර්බෝලා ලෙස හැඳින්වේ. x හි අගය 0 ට නැඹුරු වන විට, y හි අගය අනන්තය දක්වා වැඩි වන බව ඔබට පහසුවෙන් දැක ගත හැකිය. ශ්‍රිතයක ප්‍රස්ථාරය යනු ශාඛා දෙකකින් සමන්විත වන අතර විවිධ ඛණ්ඩාංක හතරක පිහිටා ඇති වක්‍රයකි.