1°

1°. Rovnice dotykovej roviny a normály pre prípad explicitnej definície povrchu.

Uvažujme jednu z geometrických aplikácií parciálnych derivácií funkcie dvoch premenných. Nechajte funkciu z = f (x;y) v bode rozlíšiteľné (x 0; y 0) nejaká oblasť DÎ R 2. Narežeme povrch S, reprezentujúci funkciu z, lietadlá x = x 0 A y = y 0(obr. 11).

Lietadlo X = x 0 pretína povrch S pozdĺž nejakej línie z 0 (y), ktorého rovnicu získame dosadením do výrazu pôvodnej funkcie z ==f (x;y) namiesto toho Xčísla x 0. Bodka M 0 (x 0;r 0,f (x 0;y 0)) patrí do krivky z 0 (y). Kvôli diferencovateľnej funkcii z v bode M 0 funkciu z 0 (y) je tiež v bode diferencovateľná y = y 0. Preto v tomto bode v rovine x = x 0 do zákruty z 0 (y) možno nakresliť dotyčnicu l 1.

Uskutočnenie podobného zdôvodnenia pre sekciu pri = r 0, postavme tangentu l 2 do zákruty z 0 (x) v bode X = x 0 - Priame 1 1 A 1 2 definovať rovinu tzv dotyková rovina na povrch S v bode M 0.

Vytvorme jeho rovnicu. Keďže rovina prechádza bodom Mo(x 0;yo;z 0), potom jeho rovnicu možno zapísať ako

A(x - xo) + B(y - yo) + C (z - zo) = 0,

ktorý sa dá prepísať takto:

z -z 0 = A 1 (x – x 0) + B 1 (y – y 0) (1)

(rozdelenie rovnice -C a označenie ).

nájdeme A 1 a B1.

Tangentové rovnice 1 1 A 1 2 vyzerať ako

resp.

Tangenta l 1 leží v rovine a , teda súradnice všetkých bodov l 1 splniť rovnicu (1). Táto skutočnosť môže byť zapísaná vo forme systému

Vyriešením tohto systému vzhľadom na B 1 dostaneme to, že vykonáme podobné uvažovanie pre dotyčnicu l 3, je ľahké to zistiť.

Nahradenie hodnôt A 1 a B 1 do rovnice (1), získame požadovanú rovnicu dotyčnicovej roviny:

Čiara prechádzajúca bodom M 0 a kolmá na dotykovú rovinu zostrojenú v tomto bode povrchu sa nazýva jeho normálne.

Pomocou podmienky kolmosti priamky a roviny je ľahké ju získať kanonické rovnice normály:

Komentujte. Vzorce pre dotykovú rovinu a normálu k povrchu sa získajú pre obyčajné, t. j. nešpeciálne body povrchu. Bodka M 0 povrch sa nazýva špeciálne, ak sa v tomto bode všetky parciálne derivácie rovnajú nule alebo aspoň jedna z nich neexistuje. Takéto body neberieme do úvahy.

Príklad. Napíšte rovnice pre dotykovú rovinu a normálu k povrchu v jej bode M(2; -1; 1).

Riešenie. Nájdite parciálne derivácie tejto funkcie a ich hodnoty v bode M

Odtiaľ, použitím vzorcov (2) a (3), budeme mať: z-1=2(x-2)+2(y+1) alebo 2x+2u-z-1=0- rovnica dotykovej roviny a - normálne rovnice.

2°. Rovnice dotykovej roviny a normály pre prípad implicitnej definície plochy.

Ak povrch S daný rovnicou F (x; y;z)= 0, potom rovnice (2) a (3), berúc do úvahy skutočnosť, že parciálne derivácie možno nájsť ako derivácie implicitnej funkcie.

Definícia 1 : Dotyková rovina k povrchu v danom bode P (x 0, y 0, z 0) je rovina prechádzajúca bodom P a obsahujúca všetky dotyčnice zostrojené v bode P ku všetkým možným krivkám na tomto povrchu prechádzajúcich bodom P.

Nech je plocha s daná rovnicou F (X, pri, z) = 0 a bod P (x 0 , r 0 , z 0) patrí k tomuto povrchu. Vyberme nejakú krivku na povrchu L, prechádzajúci bodom R.

Nechaj X = X(t), pri = pri(t), z = z(t) - parametrické rovnice linky L.

Predpokladajme, že: 1) funkcia F(X, pri, z) je v bode rozlíšiteľné R a nie všetky jeho parciálne derivácie sa v tomto bode rovnajú nule; 2) funkcie X(t), pri(t), z(t) sú tiež rozlíšiteľné.

Keďže krivka patrí k ploche s, súradnice ľubovoľného bodu na tejto krivke, ktoré sú dosadené do rovnice plochy, z nej urobia identitu. Platí teda identická rovnosť: F [x(t), pri(t), z (t)]= 0.

Rozlíšenie tejto identity vzhľadom na premennú t pomocou reťazového pravidla získame novú identickú rovnosť platnú vo všetkých bodoch krivky, vrátane bodu P (x 0 , r 0 , z 0):

Nech bod P zodpovedá hodnote parametra t 0, tj x 0 = x (t 0), r 0 = r (t 0), z 0 = z (t 0). Potom posledný vzťah vypočítaný v bode R, bude mať formu

Tento vzorec je skalárnym súčinom dvoch vektorov. Prvým je konštantný vektor

nezávisle od výberu krivky na povrchu.

Druhý vektor je dotyčnica v bode R k čiare L, čo znamená, že závisí od výberu čiary na ploche, to znamená, že ide o premenný vektor.

So zavedenými zápismi je rovnosť:

prepíšme ako.

Jeho význam je nasledovný: skalárny súčin sa rovná nule, preto sú vektory kolmé. Výber všetkých možných kriviek prechádzajúcich bodom R na ploche s budeme mať v bode zostrojené rôzne vektory dotyčníc R k týmto riadkom; vektor nezávisí od tejto voľby a bude kolmý na ktorýkoľvek z nich, to znamená, že všetky dotyčnicové vektory sú umiestnené v rovnakej rovine, ktorá je podľa definície dotyčnicou k povrchu s a bodu R v tomto prípade sa nazýva dotykový bod. Vektor je smerový vektor kolmý k povrchu.

Definícia 2: Normálou na plochu s v bode P je priamka prechádzajúca bodom P a kolmá na dotykovú rovinu zostrojenú v tomto bode.

Dokázali sme existenciu dotykovej roviny, a teda normály k povrchu. Zapíšme si ich rovnice:

Rovnica dotykovej roviny zostrojenej v bode P (x0, y0, z0) k ploche s je daná rovnicou F(x, y, z) = 0;

Rovnica normály zostrojená v bode R na povrch s.

Príklad: Nájdite rovnicu povrchu tvorenej rotáciou paraboly:

z 2 = 2p (y +2)

okolo osi y, vypočítajte za predpokladu, že bod M(3; 1; - 3) patrí k povrchu. Nájdite rovnice normály a dotykovej roviny k povrchu v bode M.

Riešenie. Pomocou pravidla na písanie rotačnej plochy získame:

z 2 + x 2 = 2p (y +2) .

Dosadením súradníc bodu M do tejto rovnice vypočítame hodnotu parametra p: 9 + 9 = 2R (1 + 2) . Zaznamenávame konečný pohľad na rotačnú plochu prechádzajúcu bodom M:

z 2 + x 2 = 6 (r +2).

Teraz nájdeme rovnice normálnej a dotyčnicovej roviny pomocou vzorcov, pre ktoré najprv vypočítame parciálne derivácie funkcie:

F(x, y) = z 2 + x 2- 6 (r +2):

Potom rovnica dotykovej roviny nadobúda tvar 6(x - 3) - 6 (y - 1) - 6 (z + 3) = 0 alebo x - y - z - 5 = 0;

Uvažujme geometrické aplikácie derivácie funkcie viacerých premenných. Nech je funkcia dvoch premenných špecifikovaná implicitne: . Táto funkcia vo svojej oblasti definície je reprezentovaná určitou plochou (časť 5.1). Zoberme si ľubovoľný bod na tejto ploche , v ktorom všetky tri parciálne derivácie , , existujú a sú spojité a aspoň jedna z nich sa nerovná nule.

Bod s takouto charakteristikou sa nazýva tzv obyčajný povrchový bod. Ak nie je splnená aspoň jedna z vyššie uvedených požiadaviek, potom sa bod nazýva špeciálne povrchový bod.

Prostredníctvom vybraného bodu na ploche možno nakresliť mnoho kriviek, z ktorých každá môže mať dotyčnicu.

Definícia 5.8.1 . Rovina, v ktorej sa nachádzajú všetky dotyčnice k priamkam na povrchu prechádzajúcich určitým bodom, sa nazýva dotyková rovina k tomuto povrchu v bode. .

Utrácať danej rovine stačí mať dve dotyčnice, teda dve krivky na ploche. Môžu to byť krivky získané ako výsledok rezania daného povrchu rovinami , (obr. 5.8.1).

Napíšme rovnicu dotyčnice ku krivke ležiacej v priesečníku plochy a roviny. Keďže táto krivka leží v súradnicovom systéme, rovnica dotyčnice k nej v bode v súlade s odsekom 2.7 má tvar:

. (5.8.1)

V súlade s tým má rovnica dotyčnice ku krivke ležiacej v priesečníku plochy a roviny v súradnicovom systéme v rovnakom bode tvar:

. (5.8.2)

Použime výraz pre deriváciu implicitne špecifikovanej funkcie (časť 5.7). Potom, eh. Nahradením týchto derivátov do (5.8.1) a (5.8.2) dostaneme:

; (5.8.3)

. (5.8.4)

Pretože výsledné výrazy nie sú nič iné ako rovnice priamych čiar v kanonická forma(položka 15), potom z (5.8.3) získame smerový vektor a od (5.8.4) – . Vektorové umelecké dielo dá vektor kolmý na dané dotyčnice a následne na dotyčnicu roviny:

Z toho vyplýva, že rovnica dotykovej roviny k povrchu v bode má tvar (položka 14):

Definícia 5.8.2 . Priama čiara vedená cez bod plocha kolmá na dotykovú rovinu v tomto bode sa nazýva normála k ploche.

Keďže smerový vektor normály k povrchu sa zhoduje s normálou k dotyčnicovej rovine, normálna rovnica má tvar:

.

Skalárne pole

Nech je oblasť špecifikovaná v priestore, zaberá časť alebo celý tento priestor. Každý bod tejto oblasti nech je podľa nejakého zákona spojený s určitou skalárnou veličinou (číslom).

Definícia 5.9.1 . Oblasť v priestore, ktorej každý bod je podľa známeho zákona spojený s určitou skalárnou veličinou, sa nazýva skalárne pole..

Ak je s oblasťou spojený nejaký druh súradnicového systému, napríklad pravouhlý karteziánsky systém, potom každý bod získa svoje vlastné súradnice. V tomto prípade sa skalárne množstvo stáva funkciou súradníc: v rovine – , v trojrozmernom priestore – . Samotná funkcia, ktorá toto pole popisuje, sa často nazýva skalárne pole. V závislosti od rozmeru priestoru môže byť skalárne pole ploché, trojrozmerné atď.

Je potrebné zdôrazniť, že veľkosť skalárneho poľa závisí iba od polohy bodu v oblasti, nezávisí však od výberu súradnicového systému.

Definícia 5.9.2 . Skalárne pole, ktoré závisí iba od polohy bodu v oblasti, ale nezávisí od času, sa nazýva stacionárne..

Nestacionárne skalárne polia, tj časovo závislé, sa v tejto časti nebudú brať do úvahy.

Príklady skalárnych polí zahŕňajú teplotné pole, tlakové pole v atmosfére a výškové pole nad hladinou oceánu.

Geometricky sú skalárne polia často reprezentované pomocou takzvaných čiar alebo rovných plôch.

Definícia 5.9.3 . Množina všetkých bodov v priestore, v ktorých je skalárne pole má rovnaký význam sa nazýva rovná plocha alebo ekvipotenciálna plocha. V plochom prípade pre skalárne pole sa táto množina nazýva úrovňová čiara alebo ekvipotenciálna čiara.

Je zrejmé, že rovnica rovinného povrchu má tvar , úrovňové čiary – . Uvedením konštanty v týchto rovniciach rôzne významy, dostaneme rodinu povrchov alebo rovných čiar. napr. (gule vnorené do seba s rôznymi polomermi) alebo (rodina elips).

Príklady úrovňových čiar z fyziky zahŕňajú izotermy (čiary rovnakej teploty), izobary (čiary rovnakého tlaku); z geodézie - čiary rovnakej výšky atď.

Totiž o tom, čo vidíte v nadpise. V podstate ide o „priestorový analóg“ problémy s hľadaním dotyčníc A normálnosti ku grafu funkcie jednej premennej, a preto by nemali nastať žiadne ťažkosti.

Začnime základnými otázkami: ČO JE tangensová rovina a ČO normála? Mnoho ľudí chápe tieto pojmy na úrovni intuície. Najjednoduchší model, ktorý príde na myseľ, je guľa, na ktorej leží tenký plochý kus kartónu. Kartón je umiestnený čo najbližšie ku gule a dotýka sa jej v jedinom bode. Okrem toho je v mieste kontaktu zaistená ihlou, ktorá trčí priamo nahor.

Teoreticky existuje pomerne dômyselná definícia dotykovej roviny. Predstavte si zadarmo povrch a bod k tomu patriaci. Je zrejmé, že cez bod prechádza veľa priestorové línie, ktoré patria k tomuto povrchu. Kto má aké asociácie? =) ...osobne som si predstavoval chobotnicu. Predpokladajme, že každý takýto riadok má priestorová dotyčnica v bode .

Definícia 1: dotyková rovina na povrch v bode - to je lietadlo, obsahujúci dotyčnice ku všetkým krivkám, ktoré patria danej ploche a prechádzajú bodom.

Definícia 2: normálne na povrch v bode - to je rovno, prechádzajúci cez tento bod kolmá na dotykovú rovinu.

Jednoduché a elegantné. Mimochodom, aby ste neumreli od nudy z jednoduchosti materiálu, o niečo neskôr sa s vami podelím o jedno elegantné tajomstvo, vďaka ktorému môžete RAZ A NAVŽDY zabudnúť na napchávanie rôznych definícií.

Zoznámime sa s pracovnými vzorcami a algoritmom riešenia na konkrétnom príklade. V drvivej väčšine problémov je potrebné zostrojiť rovnicu dotykovej roviny aj normálnu rovnicu:

Príklad 1

Riešenie:ak je povrch daný rovnicou (t.j. implicitne), potom rovnicu dotykovej roviny k danému povrchu v bode možno nájsť pomocou nasledujúceho vzorca:

Osobitnú pozornosť venujem nezvyčajným parciálnym derivátom - ich netreba zamieňať s parciálne derivácie implicitne špecifikovanej funkcie (hoci povrch je špecifikovaný implicitne). Pri hľadaní týchto derivátov sa musíte riadiť pravidlá pre diferenciáciu funkcie troch premenných, to znamená, že pri diferenciácii vzhľadom na akúkoľvek premennú sa ostatné dve písmená považujú za konštanty:

Bez toho, aby sme opustili pokladňu, nájdeme parciálny derivát v bode:

Podobne:

Toto bol najnepríjemnejší moment rozhodnutia, v ktorom sa chyba, ak nie je povolená, objavuje neustále. Existuje však efektívna technika skontrolujte, o čom som hovoril v triede Smerová derivácia a gradient.

Všetky „prísady“ boli nájdené a teraz ide o starostlivé nahradenie s ďalšími zjednodušeniami:

– všeobecná rovnica požadovanú dotykovú rovinu.

Dôrazne odporúčam skontrolovať aj túto fázu riešenia. Najprv sa musíte uistiť, že súradnice dotyčného bodu skutočne spĺňajú nájdenú rovnicu:

- skutočná rovnosť.

Teraz „odstránime“ koeficienty všeobecná rovnica roviny a skontrolujte ich zhodu alebo proporcionalitu s príslušnými hodnotami. V tomto prípade sú proporcionálne. Ako si pamätáte z kurz analytickej geometrie, - Toto normálny vektor dotyková rovina a on je tiež vodiaci vektor normálna priamka. Poďme skladať kanonické rovnice normály podľa bodového a smerového vektora:

V zásade môžu byť menovatele znížené o dva, ale nie je to potrebné

Odpoveď:

Nie je zakázané označovať rovnice nejakými písmenami, ale opäť, prečo? Tu je už úplne jasné, o čo ide.

Nasledujúce dva príklady sú pre nezávislé rozhodnutie. Malý „matematický jazykolam“:

Príklad 2

Nájdite rovnice dotykovej roviny a normály k povrchu v bode.

A úloha zaujímavá z technického hľadiska:

Príklad 3

Napíšte rovnice pre dotykovú rovinu a normálu k povrchu v bode

Na mieste.

Existuje veľká šanca, že sa nielen zmätiete, ale pri nahrávaní narazíte aj na ťažkosti kanonické rovnice priamky. A normálne rovnice, ako pravdepodobne chápete, sú zvyčajne napísané v tejto forme. Aj keď kvôli zabudnutiu alebo neznalosti niektorých nuancií je parametrická forma viac ako prijateľná.

Približné príklady konečného prevedenia riešení na konci hodiny.

Existuje v niektorom bode povrchu dotyková rovina? Vo všeobecnosti samozrejme nie. Klasickým príkladom je kužeľový povrch a bod - dotyčnice v tomto bode tvoria priamo kužeľovú plochu a samozrejme neležia v rovnakej rovine. Analyticky sa dá ľahko overiť, že niečo nie je v poriadku: .

Ďalším zdrojom problémov je skutočnosť neexistencia akákoľvek parciálna derivácia v bode. To však neznamená, že v danom bode neexistuje jedna dotyková rovina.

Bola to však skôr populárna veda než prakticky významná informácia a vraciame sa k naliehavým veciam:

Ako písať rovnice pre dotykovú rovinu a normálu v bode,
ak je povrch špecifikovaný explicitnou funkciou?

Prepíšme to implicitne:

A pomocou rovnakých princípov nájdeme parciálne derivácie:

Vzorec tangenciálnej roviny sa teda transformuje na nasledujúcu rovnicu:

A podľa toho kanonické normálne rovnice:

Ako asi tušíte, - tieto sú už „skutočné“ parciálne derivácie funkcie dvoch premenných v bode, ktorý sme zvykli označovať písmenom „z“ a našli sme ho 100 500-krát.

Upozorňujeme, že v tomto článku si stačí zapamätať úplne prvý vzorec, z ktorého je v prípade potreby ľahké odvodiť všetko ostatné (samozrejme so základnou úrovňou školenia). Presne takýto prístup by sa mal používať pri štúdiu exaktných vied, t.j. z minima informácií sa musíme snažiť „vyvodiť“ maximum záverov a dôsledkov. „Ohľaduplnosť“ a existujúce znalosti pomôžu! Tento princíp je užitočný aj preto, že vás s najväčšou pravdepodobnosťou zachráni v kritickej situácii, keď viete veľmi málo.

Poďme vypracovať „upravené“ vzorce s niekoľkými príkladmi:

Príklad 4

Napíšte rovnice pre dotykovú rovinu a normálu k povrchu v bode .

Je tu mierne prekrytie so zápismi - teraz písmeno označuje bod na rovine, ale čo sa dá robiť - také obľúbené písmeno...

Riešenie: zostavme rovnicu požadovanej dotyčnicovej roviny pomocou vzorca:

Vypočítajme hodnotu funkcie v bode:

Poďme počítať Parciálne deriváty 1. rádu v tomto bode:

Takto:

opatrne, neponáhľajte sa:

Zapíšme si kanonické rovnice normály v bode:

Odpoveď:

A posledný príklad pre vaše vlastné riešenie:

Príklad 5

Napíšte rovnice pre dotykovú rovinu a normálu k povrchu v bode.

Na záver - pretože som vysvetlil prakticky všetky technické body a nie je čo dodať. Aj samotné funkcie navrhnuté v tejto úlohe sú fádne a monotónne – v praxi takmer zaručene narazíte na „polynóm“ av tomto zmysle príklad č. 2 s exponentom vyzerá ako „čierna ovca“. Mimochodom, je oveľa pravdepodobnejšie, že sa stretne s povrchom daný rovnicou a to je ďalší dôvod, prečo bola funkcia zaradená do článku ako číslo dva.

A na záver sľúbené tajomstvo: ako sa teda vyhnúť preplneným definíciám? (Samozrejme, nemyslím situáciu, keď študent niečo pred skúškou horúčkovito napcháva)

Definícia akéhokoľvek pojmu/javu/predmetu dáva v prvom rade odpoveď na nasledujúcu otázku: ČO TO JE? (kto/takí/takí/sú). Vedome Pri odpovedi na túto otázku by ste sa mali pokúsiť zamyslieť významný znamenia, určite identifikácia konkrétneho pojmu/javu/predmetu. Áno, spočiatku sa to ukazuje ako nejaké jazykové, nepresné a nadbytočné (učiteľ vás opraví =)), ale časom sa vyvinie celkom slušná vedecká reč.

Cvičte napríklad na najabstraktnejších predmetoch, odpovedzte na otázku: kto je Cheburashka? Nie je to také jednoduché ;-) Toto je " rozprávková postava s veľkými ušami, očami a hnedou srsťou“? Ďaleko a veľmi ďaleko od definície - nikdy neviete, že existujú postavy s takými vlastnosťami... Ale toto je oveľa bližšie k definícii: „Cheburashka je postava, ktorú v roku 1966 vymyslel spisovateľ Eduard Uspenskij, ktorý ... (zoznam hlavných charakteristické črty)» . Všimnite si, ako dobre to začalo

Stiahnite si z Depositfiles

4. TEÓRIA PLOCH.

4.1 ROVNICE POVRCHU.

Povrch v trojrozmerný priestor možno dať:

1) implicitne: F ( x , r , z ) =0 (4.1)

2) výslovne: z = f ( x , r ) (4.2)

3) parametricky: (4.3)

alebo:
(4.3’)

kde sú skalárne argumenty
niekedy nazývané krivočiare súradnice. Napríklad guľa
pohodlné zasadenie sférické súradnice:
.

4.2 DOTYČNÁ ROVINA A NORMÁLNA K POVRCHU.

Ak priamka leží na povrchu (4.1), potom súradnice jej bodov spĺňajú rovnicu povrchu:

Rozlíšením tejto identity dostaneme:

(4.4)

alebo
(4.4 ’ )

v každom bode krivky na povrchu. Teda vektor gradientu v nesingulárnych bodoch povrchu (pri ktorých je funkcia (4.5) diferencovateľná a
) je kolmý na vektory dotyčníc k ľubovoľným čiaram na povrchu, t.j. môže byť použitý ako normálový vektor na zostavenie rovnice dotyčnicovej roviny v bode M 0 (x 0 , r 0 , z 0 ) povrch

(4.6)

a ako smerový vektor v normálnej rovnici:

(4.7)

V prípade explicitnej (4.2) špecifikácie povrchu majú rovnice dotyčnicovej roviny a normály tvar:

(4.8)

A
(4.9)

Pri parametrickom znázornení plochy (4.3) sa vektory
ležia v dotykovej rovine a rovnicu dotykovej roviny možno zapísať ako:

(4.10)

a ich vektorový súčin možno brať ako smerový normálový vektor:

a normálna rovnica môže byť napísaná ako:

(4.11)

Kde
— hodnoty parametrov zodpovedajúce bodu M 0 .

V nasledujúcom texte sa obmedzíme na uvažovanie len o takých povrchových bodoch, kde sú vektory

nerovná sa nule a nie je rovnobežná.

Príklad 4.1 Vytvorte rovnice pre dotykovú rovinu a normálu v bode M 0 (1,1,2) na povrch rotačného paraboloidu
.

Riešenie: Keďže paraboloidná rovnica je daná explicitne, potom podľa (4.8) a (4.9) musíme nájsť
v bode M 0 :

a v bode M 0
. Potom rovnica dotykovej roviny v bode M 0 bude vyzerať takto:

2(x -1)+2(r -1)-(z-2) = 0 alebo 2 x +2 r – z - 2=0 a normálna rovnica
.

Príklad 4.2 Zostavte rovnice pre dotykovú rovinu a normálu v ľubovoľnom bode skrutkovice
, .

Riešenie. tu ,

Rovnica dotykovej roviny:

alebo

Normálne rovnice:

.

4.3 PRVÁ ŠTVADRATICKÁ POVRCHOVÁ FORMA.

Ak je povrch daný rovnicou

potom krivka
môže to byť dané rovnicou
(4.12)

Polomerový vektorový diferenciál
pozdĺž krivky zodpovedajúcej posunutiu z bodu M 0 k najbližšiemu bodu M, sa rovná

(4.13)

Pretože
je diferenciál oblúka krivky zodpovedajúci rovnakému posunutiu), potom

(4.14)

Kde .

Výraz na pravej strane (4.14) sa nazýva prvý kvadratický tvar povrchu a hrá obrovskú úlohu v teórii povrchov.

Integrujem diferenciálds v rozmedzí od t 0 (zodpovedá bodu M 0) až t (zodpovedá bodu M), získame dĺžku zodpovedajúceho segmentu krivky

(4.15)

Keď poznáte prvý kvadratický tvar povrchu, môžete nájsť nielen dĺžky, ale aj uhly medzi krivkami.

Ak du , dv sú diferenciály krivočiarych súradníc zodpovedajúce nekonečne malému posunu pozdĺž jednej krivky a
- na druhej strane, potom berúc do úvahy (4.13):

(4.16)

Pomocou vzorca

(4.17)

prvá kvadratická forma umožňuje vypočítať plochu regiónu
povrchy.

Príklad 4.3 Na helikoide nájdite dĺžku špirály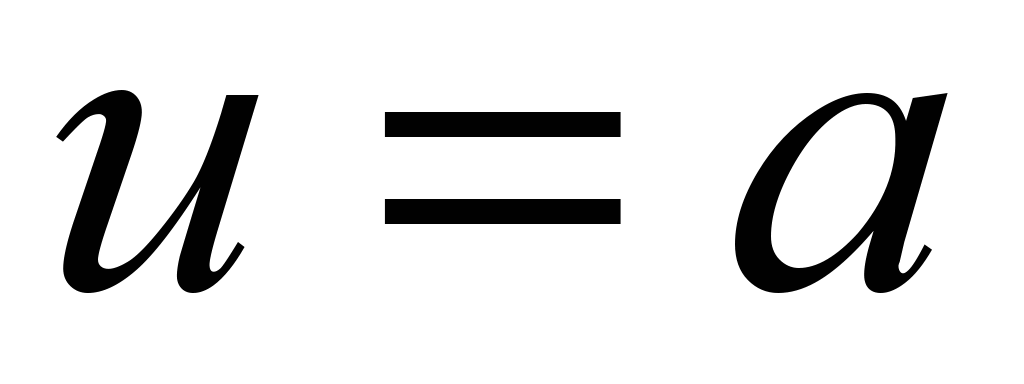
medzi dvoma bodmi.

Riešenie. Pretože na špirále
, To . Poďme nájsť v bode
prvá kvadratická forma. Po určení av = t , dostaneme rovnicu tejto špirálovej čiary v tvare . Kvadratický tvar:

= - prvý kvadratický tvar.

tu . V tomto prípade vo vzorci (4.15).
a dĺžka oblúka:

=

4.4 DRUHÝ FORMULÁR KVADRATICKEHO POVRCHU.

Označme
- jednotkový vektor kolmý k povrchu
:

(4.18) . (4.23)

Čiara na povrchu sa nazýva čiara zakrivenia, ak jej smer v každom bode je hlavným smerom.

4.6 KONCEPCIA GEODETICKÝCH ČIAR NA PLOCHE.

Definícia 4.1 . Krivka na ploche sa nazýva geodetická, ak je jej hlavnou normálou v každom bode, kde je zakrivenie nenulové, sa zhoduje s normálom na povrch.

Cez každý bod povrchu v akomkoľvek smere prechádza, a to iba jedna geodetická. Napríklad na guli sú veľké kruhy geodetikou.

Parametrizácia povrchu sa nazýva semi-geodetická, ak jedna skupina súradnicových čiar pozostáva z geodetických čiar a druhá je k nej ortogonálna. Napríklad na guli sú poludníky (geodetiky) a rovnobežky.

Geodézia na dostatočne malom segmente je najkratšia zo všetkých kriviek v jej blízkosti, ktoré spájajú rovnaké body.