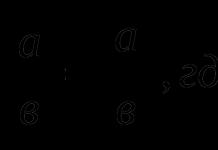
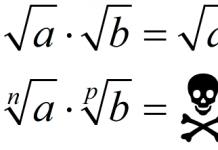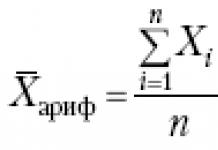Основные понятия.

Момент силы относительно оси вращения – это векторное призведение радиус-вектора на силу.

Момент силы – это вектор, направление которого определяется по правилу буравчика (правого винта) в зависимости от направления силы, действующей на тело. Момент силы направлен вдоль оси вращения и не имеет конкретной точки приложения.

Численное значение данного вектора определяется по формуле:

M=r×F × sina (1.15),

где a- угол между радиус-вектором и направлением действия силы.

Если a=0 или p , момент силы М=0 , т.е. сила, проходящяя через ось вращения или совпадающяя с ней, вращения не вызывает.

Наибольший по модулю вращающий момент создается, если сила действует под углом a=p/2 (М > 0) или a=3p/2 (М < 0).

Используя понятие плеча силы (плечо силы d – это перпендикуляр, опущенный из центра вращения на линию действия силы), формула момента силы принимает вид:

Где (1.16)

Правило моментов сил (условие равновесия тела, имеющего неподвижную ось вращения):

Для того, чтобы тело, имеющее неподвижную ось вращения, находилось в равновесии, необходимо, чтобы алгебраическая сумма моментов сил, действующих на данное тело, равнялась нулю.

S М i =0 (1.17)

Единицей измерения момента силы в системе СИ является [Н×м]

При вращательном движении инертность тела зависит не только от его массы, но и от распределения ее в пространстве относительно оси вращения.

Инертность при вращении характеризуется моментом инерциитела относительно оси вращения J.

Момент инерции материальной точки относительно оси вращения – это величина, равная произведению массы точки на квадрат ее расстояния от оси вращения:

J i =m i × r i 2 (1.18)

Моментом инерции тела относительно оси называется сумма моментов инерции материальных точек, из которых состоит тело:

J=S m i × r i 2 (1.19)

Момент инерции тела зависит от его массы и формы, а также от выбора оси вращения. Для определения момента инерции тела относительно некоторой оси используется теорема Штейнера-Гюйгенса:

J=J 0 +m× d 2 (1.20),

где J 0 – момент инерции относительно параллельной оси, проходящей через цент масс тела, d – расстояние между двумя параллельными осями. Момент инерции в СИ измеряется в [кг×м 2 ]

Момент инерции при вращательном движении туловища человека определяют опытным путем и рассчитывают приблизительно по формулам для цилиндра, круглого стержня или шара.

Момент инерции человека относительно вертикальной оси вращения, которая проходит через центр масс (центр масс тела человека находится в сагиттальной плоскости немного впереди второго крестцового позвонка), в зависимости от положения человека, имеет следующие значения: при стойке “смирно” – 1,2 кг×м 2 ; при позе «арабеск» – 8 кг×м 2 ; в горизонтальном положении – 17 кг× м 2 .

Работа во вращательном движении совершается при вращении тела под действием внешних сил.

Элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела:

dA i =M i × dj (1.21)

Если на тело действует несколько сил, то элементарная работа равнодействующей всех приложенных сил определяется по формуле:

dA=M× dj (1.22),

где М – суммарный момент всех внешних сил, действующих на тело.

Кинетическая энергия вращающегося тела W к зависит от момента инерции тела и угловой скорости его вращения:

Момент импульса (момент количества движения) – величина, численно равная произведению импульса тела на радиус вращения.

L=p× r=m× V× r (1.24).

После соответствующих преобразований можно записать формулу для определения момента импульса в виде:

(1.25).

Момент импульса – вектор, направление которого определяется по правилу правого винта. Единицей измерения момента импульса в СИ является [кг×м 2 /с]

Основные законы динамики вращательного движения.

Основное уравнение динамики вращательного движения:

Угловое ускорение тела, совершающего вращательное движение, прямо пропорционально суммарному моменту всех внешних сил и обратно пропорционально моменту инерции тела.

(1.26).

Данное уравнение играет ту же роль при описании вращательного движения, что и второй закон Ньютона для поступательного движения. Из уравнения видно, что при действии внешних сил угловое ускорение тем больше, чем меньше момент инерции тела.

Второй закон Ньютона для динамики вращательного движения можно записать в ином виде:

(1.27),

т.е. первая производная от момента импульса тела по времени равна суммарному моменту всех внешних сил, действующих на данное тело.

Закон сохранения момента импульса тела:

Если суммарный момент всех внешних сил, действующих на тело, равен нулю, т.е.

S M i =0 , тогда dL/dt=0 (1.28).

Из этого следует или (1.29).

Это утверждение составляет сущность закона сохранения момента импульса тела, который формулируется следующим образом:

Момент импульса тела остается постоянным, если суммарный момент внешних сил, действующих на вращающееся тело, равен нулю.

Этот закон является справедливым не только для абсолютно твердого тела. Примером является фигурист, который выполняет вращение вокруг вертикальной оси. Прижимая руки, фигурист уменьшает момент инерции и увеличивает угловую скорость. Чтобы затормозить вращения, он, наоборот, широко разводит руки; в результате момент инерции увеличивается, и угловая скорость вращения уменьшается.

В заключение приведем сравнительную таблицу основных величин и законов, характеризующих динамику поступательного и вращательного движений.

Таблица 1.4.

Поступательное движение	Вращательное движение
Физическая величина	Формула	Физическая величина	Формула
Масса	m	Момент инерции	J=m×r 2
Сила	F	Момент силы	M=F×r, если
Импульс тела (количество движения)	p=m×V	Момент импульса тела	L=m×V×r; L=J×w
Кинетическая энергия		Кинетическая энергия
Механическая работа	dA=FdS	Механическая работа	dA=Mdj
Основное уравнение динамики поступательного движения		Основное уравнение динамики вращательного движения	,
Закон сохранения импульса тела	или если	Закон сохранения момента импульса тела	или SJ i w i =const, если

Центрифугирование.

Разделение неоднородных систем, состоящих из частиц различной плотности, может быть произведено под действием силы тяжести и силы Архимеда (выталкивающей силы). Если есть водная суспензия частиц различной плотности, то на них действует результирующая сила

F р =F т – F А =r 1 ×V×g - r×V×g , т.е

F р =(r 1 - r)× V×g (1.30)

где V – объем частицы, r 1 и r – соответственно плотности вещества частицы и воды. Если плотности незначительно отличаются друг от друга, то результирующая сила мала и расслоение (осаждение) происходит достаточно медленно. Поэтому используют принудительное разделение частиц за счет вращения разделяемой среды.

Центрифугированием называется процесс разделения (сепарации) неоднородных систем, смесей или взвесей, состоящих из частиц различной массы, происходящий под действием центробежной силы инерции.

Основу центрифуги составляет ротор с гнездами для пробирок, расположенный в закрытом корпусе, который приводится во вращение электродвигателем. При вращении с достаточно высокой скоростью ротора центрифуги частицы взвеси, различные по масссе, под действием центробежной силы инерции распределяются слоями на различной глубине, а наиболее тяжелые осаждаются на дне пробирки.

Можно показать, что сила, под действием которой происходит сепарация, определяется по формуле:

(1.31)

где w - угловая скорость вращения центрифуги, r – расстояние от оси вращения. Эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения.

Ультрацентрифуги, работающие при скорости вращения ротора порядка 10 5 –10 6 оборотов в минуту, способны разделить частицы размером менее 100нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях.

С помощью ультрацентрифугирования можно разделить клетки на органеллы и макромолекулы. Вначале оседают (седиментируют) более крупные части (ядра, цитоскелет). При дальнейшем увеличении скорости центрифугирования последовательно оседают более мелкие частицы – сначала митохондрии, лизосомы, затем микросомы и, наконец, рибосомы и крупные макромолекулы. При центрифугировании различные фракции оседают с различной скоростью, образуя в пробирке отдельные полосы, которые можно выделить и исследовать. Фракционированные клеточные экстракты (бесклеточные системы) широко используют для изучения внутриклеточных процессов, например для изучения биосинтеза белка, расшифровки генетического кода.

Для стерилизации наконечников в стоматологии используется масляный стерилизатор с центрифугой, с помощью которой удаляется излишнее масло.

Центрифугирование можно использовать для осаждения частиц, взвешенных в моче; отделения форменных элементов от плазмы крови; разделения биополимеров, вирусов и субклеточных структур; контроля за чистотой препарата.

Задания для самоконтроля знаний.

Задание1 . Вопросы для самоконтроля.

Чем отличается равномерное движение по окружности от равномерного прямолинейного движения? При каком условии тело будет двигаться равномерно по окружности?

Объясните причину того, что равномерное движение по окружности происходит с ускорением.

Может ли криволинейное движение происходить без ускорения?

При каком условии момент силы равен нулю? принимает наибольшее значение?

Укажите границы применимости закона сохранения импульса, момента импульса.

Укажите особенности сепарации под действием силы тяжести.

Почему разделение белков с различными молекулярными массами можно проводить при помощи центрифугирования, а метод фракционной перегонки оказывается неприемлемым?

Задание 2 . Тесты для самоконтроля.

Вставьте пропущенное слово:

Изменение знака угловой скорости свидетельствует об изменении_ _ _ _ _ вращательного движения.

Изменение знака углового ускорения свидетельствует об изменении_ _ _ вращательного движения

Угловая скорость равна _ _ _ _ _производной угла поворота радиус-вектора по времени.

Угловое ускорение равно _ _ _ _ _ _производной угла поворота радиус-вектора по времени.

Момент силы равен_ _ _ _ _, если направление действующей на тело силы совпадает с осью вращения.

Найдите правильный ответ:

Момент силы зависит только от точки приложения силы.

Момент инерции тела зависит только от массы тела.

Равномерное движение по окружности происходит без ускорения.

А. Правильно. В. Неправильно.

Скалярними являются все перечисленные величины, за исключением

А. момента силы;

В. механической работы;

С. потенциальной энергии;

Д. момента инерции.

Векторными величинами являются

А. угловая скорость;

В. угловое ускорение;

С. момент силы;

Д. момент импульса.

Ответы : 1 – направления; 2 – характера; 3 – первой; 4 – второй; 5 – нулю; 6 – В; 7 – В; 8 – В; 9 – А; 10 – А, В, С, Д.

Задание 3 . Получите связь между единицами измерения:

линейной скорости см/мин и м/с;

углового ускорения рад/мин 2 и рад/с 2 ;

момента силы кН×см и Н×м;

импульса тела г×см/с и кг×м/с;

момента инерции г×см 2 и кг×м 2 .

Задание 4 . Задачи медико-биологического содержания.

Задача №1. Почему в полетной фазе прыжка спортсмен не может никакими движениями изменить траекторию движения центра тяжести тела? Совершают ли мышцы спортсмена работу при изменении положения частей тела в пространстве?

Ответ: Движениями в свободном полете по параболе спортсмен может только изменять расположение тела и его отдельных частей относительно своего центра тяжести, который в данном случае является центром вращения. Спортсмен совершает работу по изменению кинетической энергии вращения тела.

Задача №2. Какую среднюю мощность развивает человек при ходьбе, если продолжительность шага 0,5с? Считать, что работа затрачивается на ускорение и замедление нижних конечностей. Угловое перемещение ног около Dj=30 о. Момент инерции нижней конечности равен 1,7кг× м 2 . Движение ног рассматривать как равнопеременное вращательное.

Решение:

1)Запишем краткое условие задачи: Dt= 0,5с; Dj =30 0 =p/ 6; I =1,7кг× м 2

2) Определим работу за один шаг (правая и левая нога): A= 2×Iw 2 / 2=Iw 2 .

Используя формулу средней угловой скорости w ср =Dj/Dt, получим: w= 2w ср = 2×Dj/Dt; N=A/Dt= 4×I×(Dj) 2 /(Dt) 3

3) Подставим числовые значения: N =4× 1,7× (3,14) 2 /(0,5 3 × 36)=14,9(Вт)

Ответ: 14,9 Вт.

Задача №3. Какова роль движения рук при ходьбе?

Ответ : Движение ног, перемещающихся в двух параллельных плоскостях, находящихся на некотором расстоянии друг от друга, создает момент сил, стремящийся повернуть корпус человека вокруг вертикальной оси. Руками человек размахивает «навстречу» движению ног, создавая тем самым момент сил противоположного знака.

Задача №4. Одним из направлений усовершенствования бормашин, применяемых в стоматологии, является увеличение скорости вращения бора. Скорость вращения борного наконечника в ножных бормашинах составляет 1500 оборотов в минуту, в стационарных электробормашинах – 4000 об/мин, в турбинных бормашинах – уже достигает 300000 об/мин. Зачем разрабатываются новые модификации бормашин с большим числом оборотов в единицу времени?

Ответ: Дентин в несколько тысяч раз более восприимчив к болевым ощущениям, чем кожа: на 1мм 2 кожи приходится 1-2 болевые точки, а на 1мм 2 дентина резцов – до 30000 болевых точек. Увеличение числа оборотов по данным физиологов уменьшает боль при обработке кариозной полости.

Задание 5 . Заполните таблицы:

Таблица №1 . Проведите аналогию между линейными и угловыми характеристиками вращательного движения и укажите связь между ними.

Таблица №2.

Задание 6. Заполните ориентировочную карту действия:

Основные задания	Указания	Ответы
Для чего в начальной стадии исполнения сальто гимнаст сгинает колени и прижимает их к груди, а в конце вращения выпрямляет тело?	Используйте для анализа процесса понятие момента импульса и закон сохранения момента импульса.
Объясните, почему стоять на цыпочках (или держать тяжелый груз) так тяжело?	Рассмотрите условия равновесия сил и их моментов.
Как изменится угловое ускорение при увеличении момента инерции тела?	Проанализируйте основное уравнение динамики вращательного движения.
Как зависит эффект центрифугирования от разности в плотностях жидкости и частиц, которые сепарируются?	Рассмотрите силы, действующие при центрифугировании и соотношения между ними

Глава 2. Основы биомеханики.

Вопросы.

Рычаги и сочленения в опорно-двигательном аппарате человека. Понятие о степенях свободы.

Виды сокращения мышц. Основные физические величины, описывающие мышечные сокращения.

Принципы двигательной регуляции у человека.

Методы и приборы для измерения биомеханических характеристик.

2.1. Рычаги и сочленения в опорно-двигательном аппарате человека.

Анатомия и физиология двигательного аппарата человека обладают следующими особенностями, которые необходимо учитывать при биомеханических расчетах: движения тела определяются не только мышечными силами, но и внешними силами реакции, силой тяжести, инерционными силами, а также упругими силами и трением; структура двигательного аппарата допускает исключительно вращательные движения. С помощью анализа кинематических цепей поступательные движения могут быть сведены к вращательным движениям в суставах; движения управляются с помощью очень сложного кибернетического механизма, так что происходит постоянное изменение ускорений.

Опорно-двигательный аппарат человека состоит из сочлененных между собой костей скелета, к которым в определенных точках прикрепляются мышцы. Кости скелета действуют как рычаги, которые имеют точку опоры в сочленениях и приводятся в движение силой тяги, возникающей при сокращении мышц. Различают три вида рычага :

1) Рычаг, к которому действующая сила F и сила сопротивления R приложены по разные стороны от точки опоры. Примером такого рычага является череп, рассматриваемый в сагиттальной плоскости.

2) Рычаг, у которого действующая сила F и сила сопротивления R приложены по одну сторону от точки опоры, причем, сила F приложена к концу рычага, а сила R - ближе к точке опоры. Данный рычаг дает выигрыш в силе и проигрыш в расстоянии, т.е. является рычагом силы . Пример - действие свода стопы при подъеме на полупальцы, рычаги челюстно-лицевого отдела (рис. 2.1). Движения жевательного аппарата очень сложны. При закрывании рта поднимание нижней челюсти из положения максимального опускания до положения полного смыкания ее зубов с зубами верхней челюсти осуществляется движением мышц, поднимающих нижнюю челюсть. Эти мышцы действуют на нижнюю челюсть как на рычаг второго рода с точкой опоры в суставе (дающий выигрыш при жевании в силе).

3) Рычаг, у которого действующая сила приложена ближе к точке опоры, чем сила сопротивления. Данный рычаг является рычагом скорости , т.к. дает проигрыш в силе, но выигрыш в перемещении. Пример - кости предплечья.

Рис. 2.1. Рычаги челюстно-лицевого отдела и свода стопы.

Большинство костей скелета находится под действием нескольких мышц, развивающих усилия по различным направлениям. Равнодействующая их находится путем геометрического сложения по правилу параллелограмма.

Кости опорно-двигательного аппарата соединяются между собой в сочленениях или суставах. Концы костей, образующих сустав, удерживаются вместе с помощью плотно охватывающей их суставной сумки, а также прикрепленных к костям связок. Для уменьшения трения соприкасающиеся поверхности костей покрыты гладким хрящом и между ними имеется тонкий слой клейкой жидкости.

Первой ступенью биомеханического анализа двигательных процессов является определение их кинематики. На основе такого анализа строятся абстрактные кинематические цепи, подвижность или устойчивость которых может быть проверена исходя из геометрических соображений. Различают замкнутые и разомкнутые кинематические цепи, образуемые суставами и расположенными между ними жесткими звеньями.

Состояние свободной материальной точки в трехмерном пространстве задается тремя независимыми координатами – х, y, z . Независимые переменные, которые характеризуют состояние механической системы, называются степенями свободы . У более сложных систем количество степеней свободы может быть выше. Вообще, количество степеней свободы определяет не только количество независимых переменных (что характеризует состояние механической системы), но и количество независимых перемещений системы.

Число степеней свободы является основной механической характеристикой сустава, т.е. определяет число осей , вокруг которых возможно взаимное вращение сочленненых костей. Обусловлено оно главным образом геометрической формой поверхности костей, соприкасающихся в суставе.

Максимальное число степеней свободы в суставах – 3.

Примерами одноосного (плоского) сочленения в организме человека являются плечелоктевое, надпяточное и фаланговые соединения. Они допускают только возможность сгибания и разгибания с одной степенью свободы. Так, локтевая кость с помощью полукруглой выемки охватывает цилиндрический выступ на плечевой кости, который и служит осью сустава. Движения в суставе – сгибание и разгибание в плоскости, перпендикулярной оси сустава.

Лучезапястный сустав, в котором осуществляется сгибание и разгибание, а также приведение и отведение, можно отнести к суставам с двумя степенями свободы.

К суставам с тремя степенями свободы (пространственное сочленение) относятся тазобедренное и лопаточно-плечевое сочленение. Например, в лопаточно-плечевом сочленении шаровидная головка плечевой кости входит в сферическую впадину выступа лопатки. Движения в суставе – сгибание и разгибание (в сагиттальной плоскости), приведение и отведение (в фронтальной плоскости) и вращение конечности вокруг продольной оси.

Замкнутые плоские кинематические цепи обладают числом степеней свободы f F , которое вычисляется по числу звеньев n следующим образом:

Ситуация для кинематических цепей в пространстве более сложная. Здесь выполняется соотношение

(2.2)

гдеf i - число ограничений степеней свободы i- го звена.

В любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без любых специальных устройств. Они имеют название свободные оси вращения

А)Общественно-политические движения в России во второй половине XIX в. зарождение политических партий в России и их программы

Александр Лоуэн ПРЕДАТЕЛЬСТВО ТЕЛА. сгибая их в коленях. Я всегда сталкивался с тем, что шизоиды, выполняя эти движения, напрягают живот и задерживают дыхание

К неинерциальным системам отсчета часто прибегают при рассмотрении вопросов вращательного движения. Хорошо известно явление, когда на больших оборотах разваливается на куски массивный маховик. Говорят, что он разрушился под действием "центробежных сил". Понятие центробежной силы применимо лишь к неинерциальной системе отсчета, жестко связанной с вращающимся телом.

Рассмотрим простой пример вращения шарика, удерживаемого нитью, вокруг точки О (рис.3.3). В инерциальной системе отсчета на шарик действует сила натяжения нити. Уравнение движения в этой системе отсчета имеет вид

Или . (3.25)

В неинерциальной системе отсчета действуют сила натяжения нити и центробежная сила инерции. Уравнение движения в такой системе запишется так:

или , (3.26)

где – единичный вектор, направленный к центру вдоль радиуса.

Аналогично для некоторого диска, на котором к штативу подвешен шарик массой m. Диск может равномерно вращаться с некоторой угловой скоростью w . В инерциальной системе отсчета, связанной, например, с помещением, где находится диск, шарик равномерно вращается по окружности радиусом R (расстояние от точки подвеса шарика к диску до оси вращения), отклонившись от вертикального положения. Следовательно, на шарик действует сила, равная F = mw 2 ×R и направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжестиP и силы натяжения нити T :

F = P + T . (3.27)

Когда движение шарика установившееся, то

F = mg×tga = mw 2 ×R, (3.28)

tgα = ω 2 R/g. (3.29)

Таким образом, угол отклонения нити, на которой подвешен шарик, будет тем больше, чем больше расстояние R от шарика до оси вращения диска и чем больше угловая скорость вращения ω.

Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно, когда сила F уравновешивается равной по величине и противоположной по направлению силой, которая и является силой инерции F ц. Эта сила называется центробежной силой инерции. Она направлена по горизонтали в сторону от оси вращения и определяется по формуле (рис. 3.4)

F ц = - mω 2 ×R. (3.30)

Действие центробежных сил инерции проявляется в различных физических явлениях. Они широко используются во всех центробежных механизмах, где достигают больших значений. При проектировании быстро вращающихся деталей машин и механизмов принимают меры для компенсации центробежных сил инерции.

Центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении от оси вращения, не зависит от скорости тел относительно вращающихся систем отсчета. Следовательно, центробежная сила инерции действует во вращающихся системах отсчета на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе отсчета или движутся относительно нее с какой-то скоростью.

3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции. Рассмотрим проявление этой силы на одном частном примере.

Рис.3.5

Относительно вращающейся системы отсчета тело движется по окружности, лежащей в плоскости, перпендикулярной к оси вращения, причем центр окружности лежит на этой оси. Такой случай реализуется, например, когда тело движется вдоль параллели (экватора) по поверхности вращающегося земного шара (рис.3.5).

Относительно неподвижной (инерциальной) системы тело движется равномерно по окружности радиуса R. Так что ускорение тела в этой системе (центростремительное) может быть представлено в виде

где .

После выполнения простых преобразований получим

или . (3.32)

По отношению к вращающейся системе тело обладает центростремительным ускорением

Откуда следует, что первое слагаемое в (3.32) представляет собой ускорение . Следовательно,

В соответствии с этим выражением сила инерции оказывается состоящей из двух компонент:

Первая из них есть центробежная сила инерции , вторая – кориолисова сила . Сила имеет направление:

а) от центра, если скорости v ’ и wR совпадают по направлению;

б) к центру, если скорости v¢ и wR направлены в противоположные стороны.

В общем случае, когда вектор скорости v материальной точки, перемещающейся по вращающейся поверхности, направлен произвольно, математическое выражение силы Кориолиса таково:

. (3.36)

Вектор F к перпендикулярен векторам скорости v ’ тела и угловой скорости вращения ω системы отсчета в соответствии с правилом правого винта.

В таблице 3.1 наглядно показаны силы инерции, возникающие в зависимости от состояния частицы в неинерциальной системе отсчета и характера движения этой системы относительно инерциальной системы отсчета.

Таблица 3.1

Силы инерции, возникающие в неинерциальной системе
отсчета в зависимости от состояния частицы

Состояние частицы в неинерциальной системе	Название и математическое выражение силы инерции	Характер движения относительно ИСО
Частица находится в покое	Сила инерции	Система движется прямолинейно с ускорением
Центробежная сила инерции	Система вращается с угловой скоростью
Частица движется со скоростью	Кориолисова сила инерции

Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле явлений (подмывание берегов рек; неравномерное изнашивание железнодорожных рельсов; отклонение падающих на поверхность Земли тел; поведение маятника Фуко, явившееся в свое время одним из доказательств вращения Земли). Применительно к рассмотренному выше случаю движения можно привести такой пример: при стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в направлении на запад (т.е. в направлении, противоположном вращению Земли), и поднимать кверху, если выстрел произведен в восточном направлении.

Таким образом, основной закон динамики для неинерциальных систем отсчета можно записать в виде

ma ’ = F + F ин + F ц +F к, (3.37)

где F , F ин, F ц, F к - ранее рассмотренные силы, действующие в неинерциальных системах отсчета.

Надо еще раз отметить, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу. Два основных положения динамики, согласно которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются.

Для любого из тел, находящегося в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, момента импульса, энергии.

Силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил нет.

Силы инерции пропорциональны массам частиц (тел, систем) и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в "поле сил инерции" эти тела движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, находящиеся под действием сил поля тяготения.

При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном, висящем в однородном поле тяготения. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции (принципа эквивалентности Эйнштейна): «Все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы». Этот принцип является основой общей теории относительности.

3.4. Элементы динамики материальной точки и твердого тела, совершающих вращательное движение относительно неподвижной оси вращения. Основные понятия и определения: момент силы, момент импульса, момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения

Основной задачей динамики вращательного движения является задача нахождения угловых ускорений, сообщаемых известными силами. Однако одна и та же сила, в зависимости от расстояния между ее направлением и осью вращения, сообщает различные угловые ускорения. Для описания вращательного движения введены специфические параметры: момент силы, момент инерции тела, момент импульса. Благодаря этим параметрам достигается подобие основных уравнений динамики поступательного и вращательного движения.

Момент силы характеризует вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и оси вращения.

Моментом силы относительно центра вращения называют векторную физическую величину, модуль которой равен произведению модуля силы на плечо:

çM ç= çF ç×l или M = F×l, (3.38)

где l - плечо силы - кратчайшее расстояние от направления действия силы до центра вращения.

ВекторM направлен вдоль перпендикуляра к плоскости, на которой находится центр вращения и сила. Направление его определяется правилом правого винта. Так как

гдеr численное значение радиус-вектора r , который направлен из центра вращения в точку приложения силы;

α - угол между направлениямиF и r ,

M = F×r×sinα (3.39)

или в векторной форме

M = [r F ]. (3.40)

Момент нескольких сил, имеющих одну точку приложения, равен алгебраической сумме моментов слагаемых сил:

Этот момент называют главным или результирующим моментом системы сил относительно неподвижной точки вращения (центра; полюса).

Из третьего закона Ньютона следует, что моменты внутренних сил взаимодействия материальных точек системы относительно центра вращения попарно компенсируются. Следовательно, при вычислении главного момента сил необходимо учитывать только внешние силы, действующие на рассматриваемую механическую систему. Иначе результирующий момент внутренних сил системы равен нулю.

Рис.3.6

Рассмотрим вращение тела вокруг закрепленной оси (рис.3.6). Тело является абсолютно жестким. Пусть к двум точкам этого тела приложены силы , . , – радиус-вектора, проведенные из центра вращения в точку приложения силы. Предполагается, что вектора сил лежат в плоскости, перпендикулярной оси вращения. Во всяком случае, понятно, что компонента силы, параллельная оси вращения, при закрепленной оси никакого вращательного действия произвести не может.

Разложим силу на плоскости на две составляющие – касательную и нормальную к окружности, по которой движется точка приложения силы:

. (3.42)

Вращательное действие силы определяется только касательной составляющей силы и положением точки приложения силы по отношению к центру вращения, т.е. радиусом . Введем угол , образованный между направлениями векторов и . Тогда получим

(3.43)

Вращательное действие любой силы будет пропорционально произведению:

Или . (3.44)

Выражение представляет собой плечо силы, т.е. кратчайшее расстояние от линии действия силы до оси вращения.

По правилу "рычага" равновесие наступает при равенстве

Произведение носит название момента силы относительно оси вращения . Момент силы – это вектор, определяемый как векторное произведение:

. (3.46)

Модуль выражается следующим образом:

. (3.47)

Этот вектор всегда перпендикулярен плоскости, образованной векторами и , т.е. направлен по оси вращения "по правилу правого винта". Поэтому в случае закрепленной оси вращения вместо векторного представления момента силы можно воспользоваться алгебраическим представлением. Если сила вращает тело по часовой стрелке, то момент силы будем считать положительным, если сила вращает тело против часовой стрелки, то моменту этой силы будем приписывать знак "минус". Заметим, что на рис.3.6 направление оси выбрано "от нас, за чертеж". Для сил и моменты равны и . Условие равновесия может быть записано как

. (3.48)

Силы и не вызывают вращение, если их моменты и равны по величине и противоположны по направлению.

В общем случае, когда на тело действует сил, рассматривают полный момент сил:

. (3.49)

И условие равновесия тела с закрепленной осью вращения сводится к виду:

Оказывается, что один и тот же момент внешней силы, действующей на различные тела (материальные точки), сообщает им различные угловые ускорения.

Для характеристики инертности тел (материальных точек) вращательному движению вводится в рассмотрение физическая величина, называемая моментом инерции материальной точки или тела (I относительно неподвижной оси (центра вращения). Чем больше , тем меньше угловое ускорение e получит тело под действием данного момента силы .

Моментом инерции материальной точки относительно какой-либо оси или центра вращения называется физическая величина, равная произведению массы материальной точки на квадрат расстояния от нее до оси или центра вращения:

DI = Dm×r 2 . (3.51)

Момент инерции тела - величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.

Для тела с закрепленной осью вращения момент инерции представляет собой положительную скалярную величину.

Прямой способ вычисления момента инерции тела состоит в следующем: мысленно тело разбивают на совокупность материальных точек, записывают момент инерции -й материальной точки, полный момент инерции получают суммированием элементарных моментов:

1. Момент инерции обруча, вращающегося вокруг собственной оси (рис.3.7). Обруч считаем "тонким" и однородным по плотности. В данном случае все материальные точки (элементарные массы) расположены на одинаковом расстоянии от оси вращения. Поэтому

. (3.53)

2. Момент инерции стержня относительно оси, проходящей перпендикулярно к нему через его середину (рис.3.8). Стержень считаем "тонким", однородным по сечению и распределению плотности. Длина стержня – . Момент инерции материальной точки представим в виде дифференциала

где – площадь сечения.

Рис.3.9

3. Момент инерции сплошного цилиндра относительно собственной оси (рис.3.9). Цилиндр (диск) считаем однородным по плотности. Радиус цилиндра – , длина – . В данном случае целесообразно разбить цилиндр на совокупность тонкостенных цилиндров, соосных друг с другом. Элементарный момент инерции представим в виде дифференциала

Момент инерции цилиндра получим путем интегрирования:

4. Момент инерции шара относительно оси, проходящей через его центр, можно определить аналогично и вычисляется по формуле

Рис.3.10

Таким образом, момент инерции тела существенно зависит от его геометрии (формы), а также от положения оси вращения, т.е. зависит от распределения массы тела относительно оси вращения. Если выбрать новую ось вращения, оставив без изменения форму и размеры тела, то изменится и момент инерции тела. Поэтому определенный смысл момент инерции имеет только в том случае, когда задана ось вращения. Значительное упрощение в вычислениях момента инерции тела относительно оси, не проходящей через центр масс этого тела, можно получить, применяя теорему Штейнера, формулировку которой мы примем без доказательства (рис.3.10): «Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела, I 0 и произведения массы тела m 0 на квадрат расстояния между осями», т.е.

. (3.59)

Рис.3.11

Примеры применения теоремы Штейнера :

1. Момент инерции диска относительно оси , параллельной геометрической оси диска и проходящей через его край (рис.3.11).

. (3.68)

Тогда можно представить (3.67) в виде

. (3.69)

Или в векторном представлении

. (3.70)

Формулы (3.69) и (3.70) выражают основной закон динамики вращательного движения.

Выразим угловое ускорение из (3.70):

. (3.71)

Следовательно, угловое ускорение прямо пропорционально полному моменту сил, приложенных к данному телу, и обратно пропорционально моменту инерции тела относительно оси вращения.

Моментом импульса материальной точки относительно неподвижной оси (центра вращения) называется векторL , равный векторному произведению радиус-вектораr , проведенного от оси (из центра вращения О) в место нахождения материальной точки, на векторp ее импульса:

L = [r´p ] = [r´ mv ], (3.72)

где m - масса материальной точки; v - скорость материальной точки.

Моментом импульса системы (тела) относительно неподвижного центра вращения О называется геометрическая суммаL моментов импульса относительно той же точки О всех материальных точек системы:

, (3.73)

где r i , m i , v i - радиус-вектор, масса и скорость i-й материальной точки;

n - общее число этих точек в системе.

Если тело закреплено в точке О и его угловая скорость совпадает по направлению с векторомL , то момент импульса такого тела

L = Iω . (3.74)

Так как ε = dω /dt, то

. (3.75)

Формула (3.75) отображает общий вид второго закона динамики для тел, вращающихся относительно неподвижной оси; В данном виде он применим и для деформирующихся тел. При I = const формула (3.75) переходит в (3.70).

Основной закон динамики вращательного движения аналогичен второму закону Ньютона для материальной точки или тела, движущегося поступательно.

Можно указать также и закон, аналогичный третьему закону Ньютона: если одно тело действует на другое с некоторым вращающим моментом M 12 , то всегда второе тело оказывает обратное воздействие на первое с вращающим моментомM 21 , равным, но противоположно направленным:

M 12 = - M 21 . (3.76)

M× dt = dL . (3.77)

Произведение вращающего момента на время его действия M× dt называется импульсом вращающего момента . Импульс вращающего момента является вектором, ориентированным по направлению вектора M .

Пользуясь этими понятиями, второй закон механики для вращательного движения можно сформулировать следующим образом: импульс вращающего момента равен изменению момента количества движения тела, к которому приложен этот вращающий момент:

M× dt = dL = d×(Iω ). (3.78)

3.6. Сопоставление формул динамики вращательного и динамики поступательного движений

Существует очень глубокая аналогия расчетных формул, основных понятий, физических параметров теории динамики поступательного и вращательного движения. Эта аналогия позволяет глубже понять физическую сущность параметров динамики вращательного движения. Сходство между понятиями и формулами двух динамик становится очевидным, если сопоставить их с помощью таблицы. В таблицу 3.2 вошли, помимо "чисто" динамических параметров и формул, параметры и формулы кинематики поступательного и вращательного движения.

Рассмотрим самый простой случай: шарик массой т равномерно движется со скоростьюv 0 вдольрадиуса вращающегося диска. Чтобы обеспечить такое движение снабдим шарикнаправляющимстержнем, по которому он мог бы перемещаться без трения. Нитка, прикрепленная к шарику, позволит ему в радиальном направлении двигаться с постоянной скоростьюv 0 (рис. 5.6).

Рис. 5.6

Диск вращается с угловойскоростью. Опишем движение шарика в неподвижной инерциальной системе отсчётаS (x ,y ). В этой системе движение шарика складывается из двух движений: равномерного прямолинейного - по радиусу диска со скоростьюv 0 и кругового движения с угловой скоростью.

В результате сложения этих двух движений, шарик будет двигаться по криволинейной траектории - разворачивающейся спирали.

В произвольный момент времени t шарик на расстоянииr от оси вращения будет иметь радиальную скоростьv 0 и касательную - тангенциальную скорость, связанную с вращением диска (r ) (рис. 5.7).

Рис. 5.7

Посмотрим, как изменятся эти скорости шарика спустя малое время dt .

Во-первых, вся картина скоростей повернётся на угол d =dt (рис. 5.7 б). Во вторых, радиальная скорость (оставаясь неизменной по величине -V 0) получит приращение:

dV 1 =V 0 d =V 0 dt , (5.5)

связанное с повтором вектора скорости V 0 на уголd =dt .

Изменится и тангенциальная скорость. Её изменение по величине определяется тем, что шарик удалится от оси вращения на расстояние dr =V 0 dt . Поэтому:

dV 2 =(r +dr ) –r =dr =V 0 dt . (5.6)

Кроме того, эта скорость изменится на величину:

dV 3 = rd  = r dt =  2 rdt , (5.7)

в связи с поворотом вектора этой скорости на угол d .

Проанализировав все эти изменения, придём к выводу, что в радиальном направлении изменение скорости составит величину:

dV r =dV 3 = 2 rdt ,

а в тангенциальном:

dV  =dV 1 +dV 2 = 2V 0 dt .

Разделив эти изменения на промежуток времени dt , получим соответствующие компоненты ускорения:

; (5.8)

. (5.9)

Несложно ответить на вопрос: какие силы обеспечивают эти ускорения?

Центростремительное ускорение создаётся упругой силой натяжения нити (F ц.с. =F упр. =ma ц.с. =m  2 r ), направленной по радиусу к оси вращения. Касательное ускорениеa  поддерживается упругой силой деформированного стержня (
=ma  =m 2V 0). Стержень при движении прогибается и действует на шарик с силой, направленной в сторону вращения (рис. 5.8).

Рис. 5.8

Запишем уравнения движения шарика в инерциальной системе отсчёта. Это уравнения второго закона Ньютона для двух движений - вдоль радиуса:

, (5.10)

и в перпендикулярном направлении:

. (5.11)

Теперь посмотрим, как представляется движение этого же шарика наблюдателю, вращающемуся вместе с диском.

Этот наблюдатель видит, что шарик в его вращающейся системе отсчёта движется равномерно и прямолинейно со скоростью =сonst вдоль радиуса диска. Ускорение шарика равно нулю, но при этом на него действует упругая сила натяжения нитиF ц.с. =m  2 r и упругая сила деформированного стержняF =m 2V 0 . Их равнодействующая никак не может быть равна нулю.

Для того, чтобы записать уравнение движения этого тела в неинерциальной системе отсчёта в виде уравнений второго закона Ньютона, к реально действующим упругим силам прибавим две силы инерции (рис. 5.9):

(5.12)

. (5.13)

Рис. 5.9

Теперь и в радиальном и в тангенциальном направлениях суммы сил будут равны нулю, что и объясняет равномерное движение шарика вдоль радиуса.

С первой из сил инерции
мы знакомы. Это центробежная сила инерции.

Вторая сила инерции
называется силой Кориолиса.

Эти силы можно записать в векторном виде:

.

Подводя итог рассмотрению движений в неинерциальных системах отсчёта, отметим следующие основные моменты.

Ньютоновским уравнением движения можно воспользоваться и в неинерциальных системах отсчёта. Но при этом систему реально действующих сил нужно дополнить силами инерции.

В неинерциальной системе отсчёта, движущейся прямолинейно и поступательно с ускорением , сила инерции равна:

. (5.14)

В неинерциальной системе отсчёта, вращающейся с угловой скоростью , в общем случае следует ввести две силы инерции:

центробежную
, (5.15)

и кориолисову
. (5.16)

Диск вращается вокруг вертикальной оси с угловой скоростью (опыт)

На диске, на разных расстояниях от оси вращения установлены ма­ятники (на нитях подвешены ша­рики массой m). При вращении диска маятники отклоняются от вертикали на некоторый угол а.

ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА (анализ данных )__

В системе отсчета, связанной, например, с помещением, шарик равно­мерно вращается по окружности радиусом R (расстояние от центра вра­щающегося шарика до оси вращения). Следовательно, на него действует сила, равная F = m ω 2 R и направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести и силы натяжения нити . Для установившегося движения шарика , откуда

tg = ω 2 R/g ( тем больше, чем больше R и ω).

НЕИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА (анализ данных )__

В системе отсчета, связанной с вращающимся диском, шарик покоится, что возможно, если сила уравновешивается равной и противоположно направленной ей силой , которая является не чем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Сила F ц, называемая центробежной силой инерции , направлена по горизонтали от оси вращения диска, F ц = -m·ω 2 R.

Действию центробежных сил инерции под­вергаются, например, пассажиры в движущемся транспорте на поворотах, лет­чики при выполнении фигур высшего пилотажа. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов и т. д.) принимаются специальные меры для уравновешивания центробежных сил инерции.

♦ Центробежная сила инерции (F ц = -m·ω 2 R)не зависит от скорости тел относи­тельно вращающихся систем отсчета, т. е. действует на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе или движутся относительно нее с какой-то скоростью.

6.3. СИЛЫ ИНЕРЦИИ, ДЕЙСТВУЮЩИЕ НА ТЕЛО, ДВИЖУЩЕЕСЯ ВО ВРАЩАЮЩЕЙСЯ СИСТЕМЕ ОТСЧЕТА _

Диск покоится (опыт)

Шарик массой т, направленный вдоль радиуса диска со скоростью V" = const, движется по радиальной пря­мой ОА.

Диск вращается равномерно (со = const) (опыт)

Шарик массой т, движущийся со скоростью V" = const (V" ┴ ω), катится по кривой АВ, причем его скорость V" относительно диска изменяет свое направление. Это возможно лишь тогда, если на шарик действует сила, перпендикулярная скорости V".

Анализ опытных данных

Чтобы шарик катился по вращающемуся диску вдоль радиуса, использу­ют жестко укрепленный вдоль радиуса диска стержень, на котором ша­рик движется без трения равномерно и прямолинейно со скоростью . При отклонении шарика стержень действует на него с некоторой силой . Относительно диска (вращающейся системы отсчета) шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила урав­новешивается приложенной к шарику силой инерции , перпендику­лярной скорости . Эта сила называется кориолисовой силой инерции. Сила Кориолиса .

Примеры проявления сил инерции . Если тело движется в северном полушарии на север, то действующая на него сила Кориолиса направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Поэтому в северном полушарии наблюдается более сильное подмыва­ние правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д.

Допустим, что твердое тело А (рис. 1.19, а) может вращаться вокруг некоторой неподвижной оси. Для того чтобы вызвать вращение тела (изменить его угловую скорость), необходимо внешнее воздействие. Однако сила направление которой проходит через ось вращения, или сила параллельная оси, не могут изменить угловую скорость тел.

Поэтому из приложенной к телу внешней силы необходимо выделить составляющие не вызывающие вращения. Вращение может быть вызвано только силой (вращаюшей силой), лежащей в плоскости, перпендикулярной оси вращения и направленной по касательной к окружности, которую описывает точка ее приложения.

Заметим, что при вращении тела составляющие работы не совершают, так как точка приложения этих сил перемещается перпендикулярно их направлениям. Работу совершает только вращающая сила она является проекцией действующей на тело силы на направление движения точки приложения этой силы.

Определим величину работы которую совершает вращающая сила, если точка приложения ее смещается по окружности радиуса на (рис. 1.19, б). Предположим, что величина силы при этом остается постоянной. Тогда

Произведение вращающей силы на радиус есть момент вращающей силы, или вращающий момент, действующий на данное тело, и обозначается через (напомним, что моментом данной силы относительно какой-нибудь оси называется произведение этой силы на ее плечо, т. е. на длину перпендикуляра, проведенного от указанной

оси до направления действия силы). Таким образом, в формуле (2.8)

следовательно, работа, совершаемая вращающим моментом, равна произведению этого момента на угол поворота тела:

Если вращающий момент (сила или ее плечо ) с течением времени изменяется, то совершаемая работа определяется как сумма:

Момент вращающей силы представляется в виде вектора, совпадающего с осью вращения; положительную ориентировку этого вектора выбирают в том направлении, в котором перемещался бы правый винт, вращаемый этим моментом.

Вращающий момент приложенный к телу, сообщает ему некоторое угловое ускорение согласно выбранным нами направлениям векторов они ориентированы по оси вращения в одну и ту же сторону. Связь между величиной вращающего момента и величиной сообщаемого им углового ускорения можно установить двумя способами:

а) можно воспользоваться тем, что работа движущей силы равна изменению кинетической энергии тела, к которому эта сила приложена: Для вращающегося тела, согласно формулам (2.9) и (2.4), имеем

Здесь мы предполагаем, что момент инерции тела при вращении не изменяется. Разделив это уравнение на и сократив на получаем

б) можно воспользоваться тем, что момент вращающей силы равен сумме моментов сил, которые сообщают отдельным составным частям тела тангенциальные ускорения эти силы равны а их моменты -

Заменим тангенциальные ускорения на угловое ускорение, которое одинаково для всех частиц вращающегося тела (если тело при вращении не деформируется): Тогда

Формула (2.12) выражает основной закон динамики вращательного движения твердых (недеформирую-щихся) тел, для которых

угловое ускорение, приобретаемое телом под действием данного вращающего момента прямо пропорционально величине этого момента и обратно пропорционально моменту инерции тела относительно оси вращения:

В векторной форме этот закон записывается в виде

Если тело при вращении деформируется, то момент инерции его относительно оси вращения будет изменяться. Мысленно представим вращающееся тело состоящим из множества элементарных (точечных) частей; тогда деформация всего тела будет означать изменение расстояний от этих частей тела до оси вращения. Однако изменение расстояния данной угловой скорости вращения со будет сопровождаться изменением линейной скорости движения этой частицы следовательно, и ее кинетической энергии. Таким образом, при постоянной угловой скорости вращения тела изменение расстояний (следовательно, изменение момента инерции тела) будет сопровождаться изменением кинетической энергии вращения всего тела.

Из формулы (2.4), если полагать переменным, можно получить

Первое слагаемое показывает изменение кинетической энергии вращающегося тела, которое произошло только вследствие изменения угловой скорости вращения (при данном моменте инерции тела), а второе слагаемое показывает изменение кинетической анергии, которое произошло только вследствие изменения момента инерции тела (при данной угловой скорости вращения).

Однако при изменении расстояния от точечного тела до оси вращения внутренние силы, связывающие это тело с осью вращения, будут совершать работу: отрицательную, если тело удаляется, и положительную, если тело приближается к оси вращения; эта работа может быть рассчитана, если полагать, что сила, связывающая частицу с осью вращения, численно равна центростремительной силе:

Для всего тела, состоящего из множества частиц с массами получим

В общем случае, когда на тело действует внешний вращающий момент изменение кинетической энергии должно быть приравнено сумме двух работ: внешнего вращающего момента и внутренних сил При ускоренном вращении величины будут иметь положительные знаки, - отрицательный

знак (так как частицы тела удаляются от оси вращения); тогда

Подставив сюда значение из выражения (2.15) и заменив на получим

или после сокращения

Это есть общий вид основного закона механики для тел, вращающихся относительно неподвижной оси он применим и для деформирующихся тел. При формула (2.16) переходит в формулу (2.14).

Заметим, что у деформирующихся тел изменение угловой скорости вращения возможно и при отсутствии внешнего вращающего момента. Действительно, при -из формулы (2.16) получаем:

В этом случае угловая скорость вращения со изменяется только вследствие изменения момента инерции тела, вызванного внутренними силами.