1°

1°. Рівняння дотичної площини та нормалі для випадку явного завдання поверхні.

Розглянемо один із геометричних додатків приватних похідних функції двох змінних. Нехай функція z = f (x;y)диференційована в точці (x 0; у 0)деякої області DÎ R 2. Розсічемо поверхню S ,зображуючу функцію z,площинами х = х 0і у = у 0(Рис. 11).

Площина х = x 0перетинає поверхню Sпо деякій лінії z 0 (y),рівняння якої виходить підстановкою у вираз вихідної функції z ==f (x;y)замість хчисла х 0 .Крапка M 0 (x 0;y 0,f (x 0;y 0))належить кривою z 0 (y).В силу функції, що диференціюється zу точці М 0функція z 0 (y)також є диференційованою в точці у = 0 .Отже, у цій точці в площині х = х 0до кривої z 0 (y)може бути проведена дотична l 1 .

Проводячи аналогічні міркування для перерізу у = у 0 ,побудуємо дотичну l 2до кривої z 0 (x)у точці х = x 0 -Прямі 1 1 і 1 2 визначають площину, яка називається дотичною площиноюдо поверхні Sу точці М0.

Складемо її рівняння. Так як площина проходить через точку Mo (x 0;y 0;z 0),то її рівняння може бути записано у вигляді

А (х - хо) + В (у - уо) + C (z - zo) = 0,

яке можна переписати так:

z -z 0 = A 1 (x - x 0) + B 1 (y - у 0) (1)

(розділивши рівняння на -С і позначивши ).

Знайдемо A 1та B 1 .

Рівняння дотичних 1 1 і 1 2 мають вигляд

відповідно.

Стосовна l 1лежить у площині a , отже, координати всіх точок l 1задовольняють рівняння (1). Цей факт можна записати у вигляді системи

Дозволяючи цю систему щодо B 1 отримаємо, що .Проводячи аналогічні міркування для дотичної l 3легко встановити, що .

Підставивши значення А 1і B 1 рівняння (1), отримуємо шукане рівняння дотичної площини:

Пряма, що проходить через точку М 0і перпендикулярна дотичній площині, побудованій у цій точці поверхні, називається її нормаллю.

Використовуючи умову перпендикулярності прямої та площини, легко отримати канонічні рівняння нормалі:

Зауваження.Формули дотичної площини та нормалі до поверхні отримані для звичайних, тобто не особливих точок поверхні. Крапка М 0поверхні називається особливою,якщо у цій точці всі приватні похідні дорівнюють нулю або хоча б одна з них не існує. Таких точок ми не розглядаємо.

приклад. Написати рівняння дотичної площини та нормалі до поверхні у її точці М(2; -1; 1).

Рішення. Знайдемо приватні похідні цієї функції та їх значення у точці М

Звідси, застосовуючи формули (2) і (3), матимемо: z-1=2(х-2)+2(у+1)або 2х+2у-z-1=0- рівняння дотичної площини та - Рівняння нормалі.

2 °. Рівняння дотичної площини та нормалі для випадку неявного завдання поверхні.

Якщо поверхня Sзадана рівнянням F (x; у;z)= 0, то рівняння (2) і (3), з огляду на те, що приватні похідні можуть бути знайдені як похідні неявної функції.

Визначення 1 : Стосовною площиною до поверхні в даній точці P (x 0 , y 0 , z 0) називається площина, що проходить через точку Р і містить у собі всі дотичні, побудовані в точці Р до всіляких кривих на цій поверхні, що проходять через точку Р.

Нехай поверхня s задана рівнянням F (х, у, z) = 0 і точка P (x 0 , y 0 , z 0) належить цій поверхні. Виберемо на поверхні якусь криву L, що проходить через точку Р.

Нехай х = х(t), у = у(t), z = z(t) - параметричні рівняннялінії L.

Припустимо, що: 1) функція F(х, у, z) диференційована в точці Рі всі її приватні похідні у цій точці дорівнюють нулю; 2) функції х(t), у(t), z(t) також диференційовані.

Оскільки крива належить поверхні s, координати будь-якої точки цієї кривої, будучи підставленими в рівняння поверхні, звернуть його в тотожність. Таким чином, справедлива тотожна рівність: F [x(t), у(t), z (t)]= 0.

Продиференціювавши це тотожність щодо змінної t, використовуючи ланцюгове правило, отримаємо нову тотожну рівність, справедливу у всіх точках кривої, в тому числі і в точці P (x 0 , y 0 , z 0):

Нехай точці Р відповідає значення параметра t 0 , тобто x 0 = x (t 0), y 0 = y (t 0), z 0 = z (t 0). Тоді останнє співвідношення, обчислене у точці Р, набуде вигляду

Ця формула є скалярним добутком двох векторів. Перший - постійний вектор

що не залежить від вибору кривої на поверхні.

Другий вектор - дотичний у точці Рдо лінії L, Отже, залежить від вибору лінії на поверхні, тобто є змінним вектором.

При введених позначеннях рівність:

перепишемо як.

Його зміст такий: скалярний твір дорівнює нулю, отже, вектори та перпендикулярні. Вибираючи різні криві, що проходять через точку Рна поверхні s, ми матимемо різні дотичні вектори, побудовані в точці Рдо цих ліній; вектор же від цього вибору не залежить і буде перпендикулярним будь-якому з них, тобто всі дотичні вектори розташовані в одній площині, яка, за визначенням, є дотичною до поверхні s, а точка Ру цьому випадку називається точкою торкання. Вектор є напрямним вектор нормалі до поверхні.

Визначення 2: Нормаллю до поверхні s у точці Р називається пряма, що проходить через точку Р та перпендикулярна до дотичної площини, побудованої у цій точці.

Ми довели існування дотичної площини, а отже, і нормали до поверхні. Запишемо їх рівняння:

Рівняння дотичної площини, побудованої в точці P (x0, y0, z0) до поверхні s заданої рівнянням F(х, у, z) = 0;

Рівняння нормалі, побудованої у точці Рдо поверхні s.

Приклад:Знайти рівняння поверхні, утвореної обертанням параболи:

z 2 = 2p (y +2)

навколо осі оу, обчислити за умови, що точка М(3, 1, - 3)належить поверхні. Знайти рівняння нормалі та дотичної площини до поверхні у точці М.

Рішення.Використовуючи правило запису поверхні обертання, отримаємо:

z 2 + x 2 = 2p (y +2) .

Підставивши координати точки М на це рівняння, обчислимо значення параметра р: 9 + 9 = 2р(1 + 2) . Записуємо остаточний вигляд поверхні обертання, що проходить через крапку М:

z 2 + x 2 = 6 (y +2).

Тепер знайдемо рівняння нормалі та дотичної площини за формулами, для чого обчислимо спочатку приватні похідні функції:

F(x, y) = z 2 + x 2- 6 (y +2):

Тоді рівняння дотичної площини набуде вигляду 6(х - 3) - 6(y - 1) - 6(z + 3) = 0 або x - y - z - 5 = 0;

Розглянемо геометричні додатки похідної функції кількох змінних. Нехай функція двох змінних задана неявно: . Ця функція в області визначення зображується деякою поверхнею (п. 5.1). Візьмемо на цій поверхні довільну точку , в якій усі три приватні похідні , , існують і безперервні, причому хоча б одна з них не дорівнює нулю.

Крапка з такими характеристиками називається звичайною точкою поверхні. Якщо хоча б одна із зазначених вище вимог не виконується, то точка називається особливою точкою поверхні.

Через обрану на поверхні точку можна провести множину кривих, до кожної з яких може бути проведена дотична.

Визначення 5.8.1 . Площина, в якій розташовані всі прямі дотичні до ліній на поверхні, що проходять через деяку точку , називається дотичною площиною до даної поверхні в точці .

Щоб провести цю площинудостатньо мати дві дотичні прямі, тобто дві криві на поверхні. Це можуть бути криві, отримані в результаті перерізу даної поверхні площинами (рис. 5.8.1).

Запишемо рівняння дотичної лінії до кривої, що лежить на перетині поверхні та площині. Оскільки дана крива лежить у системі координат , то рівняння дотичної до неї в точці , відповідно до п. 2.7, має вигляд:

. (5.8.1)

Відповідно, рівняння дотичної до кривої, що лежить на перетині поверхні та площини, в системі координат у тій же точці має вигляд:

. (5.8.2)

Скористаємося виразом для похідної неявно заданої функції (п. 5.7). Тоді, а. Підставляючи ці похідні (5.8.1) і (5.8.2), отримаємо, відповідно:

; (5.8.3)

. (5.8.4)

Оскільки отримані вирази не що інше, як рівняння прямих у канонічній формі (п. 15), то з (5.8.3) отримуємо напрямний вектор , а з (5.8.4) – . Векторний витвірдасть вектор, нормальний до даних дотичних ліній, а, отже, до дотичної площині:

Звідси випливає, що рівняння дотичної площини до поверхні у точці має вигляд (п. 14):

Визначення 5.8.2 . Пряма, проведена через точку поверхні перпендикулярно дотичній площині в цій точці називається нормаллю до поверхні.

Оскільки напрямний вектор нормалі до поверхні збігається з нормаллю до дотичної площини, то рівняння нормалі має вигляд:

.

Скалярне поле

Нехай у просторі задана область , що займає частину або весь цей простір. Нехай кожній точці цієї області за якимсь законом поставлена ​​у відповідність деяка скалярна величина (число).

Визначення 5.9.1 . Область у просторі, кожній точці якої ставиться у відповідність за відомим законом деяка скалярна величина, називається скалярним полем.

Якщо з областю пов'язана якась система координат, наприклад, прямокутна декартова, то кожна точка набуває своїх координат. І тут скалярна величина стає функцією координат: на площині – , у тривимірному просторі – . Скалярним полем часто називають і саму функцію, що описує це поле. Залежно від розмірності простору скалярне поле може бути плоским, тривимірним і т.д.

Необхідно підкреслити, що величина скалярного поля залежить від положення точки в області , але не залежить від вибору системи координат.

Визначення 5.9.2 . Скалярне поле, що залежить тільки від положення точки в області, але не залежить від часу, називається стаціонарним.

Нестаціонарні скалярні поля, тобто залежні від часу, у цьому розділі нами не розглядатимуться.

Як приклади скалярних полів можна назвати поле температур, поле тисків в атмосфері, поле висот над рівнем океану.

Геометрично скалярні поля часто зображуються з допомогою так званих ліній чи поверхонь рівня.

Визначення 5.9.3 . Безліч всіх точок простору, в яких скалярне поле має одне й те саме значення називається поверхнею рівня або еквіпотенційною поверхнею. У плоскому випадку для скалярного поля ця множина називається лінією рівня або еквіпотенційною лінією.

Очевидно, що рівняння поверхні рівня має вигляд , лінії рівня -. Надаючи в цих рівняннях константі різні значенняотримуємо сімейство поверхонь або ліній рівня. Наприклад, (Вкладені одна в одну сфери з різними радіусами) або (родина еліпсів).

Як приклади ліній рівня з фізики можна навести ізотерми (лінії рівних температур), ізобари (лінії рівних тисків); з геодезії – лінії рівних висот тощо.

Зокрема, про те, що ви бачите в заголовку. Фактично, це «просторовий аналог» завдання знаходження дотичноїі нормалідо графіка функції однієї змінної, і тому жодних труднощів виникнути не повинно.

Почнемо з базових питань: ЩО ТАКЕ дотична площина і ЩО ТАКЕ нормаль? Багато хто усвідомлює ці поняття на рівні інтуїції. Найпростіша модель, що спадає на думку – це куля, на якій лежить тонка плоска картонка. Картонка розташована максимально близько до сфери та стосується її в єдиній точці. Крім того, в точці торкання вона закріплена голкою, що стирчить строго вгору.

Теоретично існує досить дотепне визначення дотичної площині. Уявіть довільну поверхняі точку, що їй належить. Очевидно, що через точку проходить багато просторових лінійякі належать даній поверхні. У кого які асоціації? =) … особисто я представив восьминога. Припустимо, що кожна така лінія існує просторова дотичнау точці.

Визначення 1: дотична площинадо поверхні у точці – це площина, Що містить дотичні до всіх кривих, які належать даній поверхні і проходять через точку .

Визначення 2: нормальдо поверхні у точці – це пряма, що проходить через цю точку перпендикулярно дотичній площині.

Просто та витончено. До речі, щоб ви не померли з нудьги від простоти матеріалу, трохи пізніше я поділюся з вами одним витонченим секретом, який дозволяє РАЗ І НАЗАВЖДИ забути про зубріжку різних визначень.

З робочими формулами та алгоритмом рішення познайомимося прямо на конкретному прикладі. У переважній більшості завдань потрібно скласти і рівняння дотичної площини, і рівняння нормалі:

Приклад 1

Рішення:якщо поверхня задана рівнянням (тобто неявно), то рівняння дотичної площини до даної поверхні в точці можна знайти за такою формулою:

Особливу увагу звертаю на незвичайні приватні похідні. не слід плутатиз приватними похідними неявно заданої функції (хоча поверхня задана неявно). При знаходженні цих похідних слід керуватися правилами диференціювання функції трьох змінних, тобто, при диференціюванні по будь-якій змінній, дві інші літери вважаються константами:

Не відходячи від каси, знайдемо похідну в точці:

Аналогічно:

Це був найнеприємніший момент рішення, в якому помилка якщо не допускається, то постійно здається. Тим не менш, тут існує ефективний прийом перевірки, про який я розповідав на уроці Похідна за напрямом та градієнт.

Усі «інгредієнти» знайдені і тепер справа за акуратною підстановкою з подальшими спрощеннями:

– загальне рівнянняшуканої дотичної площини.

Настійно рекомендую проконтролювати цей етап рішення. Спочатку потрібно переконатися, що координати точки дотику справді задовольняють знайденому рівнянню:

- Правильна рівність.

Тепер «знімаємо» коефіцієнти загального рівнянняплощині і перевіряємо їх щодо збігу чи пропорційності з відповідними значеннями . У разі пропорційні. Як ви пам'ятаєте з курсу аналітичної геометрії, - це вектор нормалідотичної площини, і він же – напрямний векторнормальної прямої. Складемо канонічні рівняннянормалі по точці і напрямному вектору:

У принципі, знаменники можна скоротити на «двійку», але особливої ​​потреби в цьому немає

Відповідь:

Рівняння можна позначити якими-небудь літерами, проте, знову ж таки – навіщо? Тут і так цілком зрозуміло, що до чого.

Наступні два приклади для самостійного рішення. Невелика «математична скоромовка»:

Приклад 2

Знайти рівняння дотичної площини та нормалі до поверхні у точці.

І завдання, цікаве з технічного погляду:

Приклад 3

Скласти рівняння дотичної площини та нормалі до поверхні у точці

У точці.

Тут є всі шанси не тільки заплутатися, а й зіткнутися з труднощами під час запису канонічних рівнянь прямої. А рівняння нормалі, як ви, мабуть, зрозуміли, заведено записувати саме в такому вигляді. Хоча, через забудькуватість або незнання деяких нюансів більш ніж прийнятна і параметрична форма.

Зразки чистового оформлення рішень наприкінці уроку.

У будь-якій точці поверхні існує дотична площина? Загалом, звичайно, ні. Класичний приклад – це конічна поверхня і точка - дотичні у цій точці безпосередньо утворюють конічну поверхню, і, зрозуміло, не лежать в одній площині. У негараздах легко переконатися і аналітично: .

Іншим джерелом проблем є факт неіснуваннябудь-якої приватної похідної в точці. Однак це ще не означає, що в цій точці немає єдиної площини.

Але це була, скоріше, науково-популярна, ніж практично значуща інформація, і ми повертаємося до справ насущних:

Як скласти рівняння дотичної площини та нормалі в точці,
якщо поверхня задана явною функцією?

Перепишемо її в неявному вигляді:

І за тими ж принципами знайдемо приватні похідні:

Таким чином, формула дотичної площини трансформується у наступне рівняння:

І, відповідно, канонічні рівняння нормалі:

Як неважко здогадатися, – це вже «справжні» приватні похідні функції двох змінниху точці , які ми звикли позначати буквою «зет» і знаходили 100 500 разів.

Зауважте, що у цій статті досить запам'ятати найпершу формулу, з якої у разі потреби легко вивести все інше (зрозуміло, маючи базовий рівень підготовки). Саме такий підхід слід використовувати під час вивчення точних наук, тобто. з мінімуму інформації треба прагнути «витягувати» максимум висновків та наслідків. «Розумів» і вже наявні знання на допомогу! Цей принцип корисний ще й тим, що з великою ймовірністю врятує критичної ситуації, коли ви знаєте дуже мало.

Відпрацюємо «модифіковані» формули кількома прикладами:

Приклад 4

Скласти рівняння дотичної площини та нормалі до поверхні у точці.

Невелика тут накладка вийшла з позначеннями – тепер буква позначає точку площини, але що вдієш – така вже популярна буква….

Рішення: рівняння шуканої дотичної площини складемо за формулою:

Обчислимо значення функції в точці:

Обчислимо приватні похідні 1-го порядкуу цій точці:

Таким чином:

акуратно, не поспішаємо:

Запишемо канонічні рівняння нормалі в точці:

Відповідь:

І заключний приклад для самостійного вирішення:

Приклад 5

Скласти рівняння дотичної площини та нормалі до поверхні у точці.

Останній – тому, що практично всі технічні моменти я роз'яснив і додати особливо нічого. Навіть самі функції, пропоновані в даному завданні, сумні й одноманітні – майже гарантовано на практиці вам попадеться «багаточлен», і в цьому сенсі Приклад №2 з експонентою виглядає «білою вороною». До речі, набагато вірогідніше зустріти поверхню, задану рівняннямі це ще одна причина, через яку функція увійшла до статті «другим номером».

І насамкінець обіцяний секрет: як же уникнути зубріння визначень? (я, звичайно, не маю на увазі ситуацію, коли студент щось гарячково зубрить перед іспитом)

Визначення будь-якого поняття/явлення/об'єкта насамперед дає відповідь на наступне запитання: ЩО ЦЕ ТАКЕ? (хто/така/ такий/такі). Усвідомленовідповідаючи на це питання, ви повинні постаратися відобразити суттєвіознаки, однозначноідентифікують те чи інше поняття/явище/об'єкт. Так, спочатку це виходить дещо недорого, неточно і надмірно (виклад поправить =)), але з часом розвивається цілком гідна наукова мова.

Потренуйтесь на абстрактних об'єктах, наприклад, дайте відповідь на запитання: хто такий Чебурашка? Не так все просто;-) Це « казковий персонажз великими вухами, очима та коричневою вовною»? Далеко і дуже далеко від визначення – чи мало персонажів з такими характеристиками…. А ось це вже набагато ближче до визначення: "Чебурашка - це персонаж, придуманий письменником Едуардом Успенським в 1966 р, який ... (перерахування основних відмінних ознак)". Зверніть увагу, як грамотно розпочато

Завантажити з Depositfiles

4. ТЕОРІЯ ПОВЕРХНІВ.

4.1 РІВНЯННЯ ПОВЕРХНОСТЕЙ.

Поверхня в тривимірному просторі може бути задана:

1) неявно: F ( x , y , z ) =0 (4.1)

2) явно: z = f ( x , y ) (4.2)

3) параметрично: (4.3)

або:
(4.3’)

де скалярні аргументи
іноді називають криволінійними координатами. Наприклад, сферу
зручно ставити в сферичних координатах:
.

4.2 ЩОДО ПЛОСКІСТЬ І НОРМАЛЬ ДО ПОВЕРХНІ.

Якщо лінія лежить на поверхні (4.1), то координати її точок задовольняють рівняння поверхні:

Диференціюючи це тотожність, отримаємо:

(4.4)

або
(4.4 ’ )

у кожній точці кривої на поверхні. Таким чином, вектор градієнта в неособливих точках поверхні (у яких функція (4.5) диференційована і
) перпендикулярний дотичних векторів до будь-яких ліній на поверхні, тобто може бути використаний як вектор нормалі для складання рівняння дотичної площини в точці М 0 (x 0 , y 0 , z 0 ) поверхні

(4.6)

і як напрямний вектор у рівнянні нормалі:

(4.7)

У разі явного (4.2) завдання поверхні рівняння дотичної площини та нормалі відповідно наберуть вигляду:

(4.8)

і
(4.9)

При параметричному поданні поверхні (4.3) вектори
лежать у дотичній площині і рівняння дотичної площини може бути записане у вигляді:

(4.10)

а як напрямний вектор нормалі може бути прийнято їх векторний твір:

і рівняння нормалі може бути записано у вигляді:

(4.11)

де
— значення параметрів відповідні точці М 0 .

Надалі ми обмежимося розглядом лише таких точок поверхні, де вектори

не рівні нулю та не паралельні.

Приклад 4.1 Скласти рівняння дотичної площини та нормалі у точці М 0 (1,1,2) до поверхні параболоїда обертання
.

Рішення: Так як рівняння параболоїда задано у явному вигляді, то згідно (4.8) та (4.9) потрібно знайти
у точці М 0 :

, А в точці М 0
. Тоді рівняння дотичної площини у точці М 0 набуде вигляду:

2(x -1)+2(y -1)-(z-2) = 0 або 2 x +2 y - z ‑ 2=0, а рівняння нормалі
.

Приклад 4.2 Скласти рівняння дотичної площини та нормалі у довільній точці гелікоїда
, .

Рішення. Тут ,

Рівняння дотичної площини:

або

Рівняння нормалі:

.

4.3 ПЕРША КВАДРАТИЧНА ФОРМА ПОВЕРХНІ.

Якщо поверхня задається рівнянням

то крива
на ній може бути задана рівнянням
(4.12)

Диференціал радіус-вектора
вздовж кривої, що відповідає зсуву з точки М 0 у прилеглу точку М, дорівнює

(4.13)

Так як
- Диференціал дуги кривої, що відповідає тому ж зсуву), то

(4.14)

де.

Вираз у правій частині (4.14) називається першою квадратичною формою поверхні і грає теоретично поверхонь величезну роль.

Інтегрую диференціалdsв межах від t 0 (відповідає точці М 0) до t (відповідає точці М), отримаємо довжину відповідного відрізка кривої

(4.15)

Знаючи першу квадратичну форму поверхні, можна знаходити не лише довжини, а й кути між кривими.

Якщо du , dv - Диференціали криволінійних координат, що відповідають нескінченно малому зміщенню по одній кривій, а
- Іншою, то з урахуванням (4.13):

(4.16)

За допомогою формули

(4.17)

перша квадратична форма дає можливість обчислити площу області
поверхні.

Приклад 4.3 На гелікоїді , знайти довжину гвинтової лінії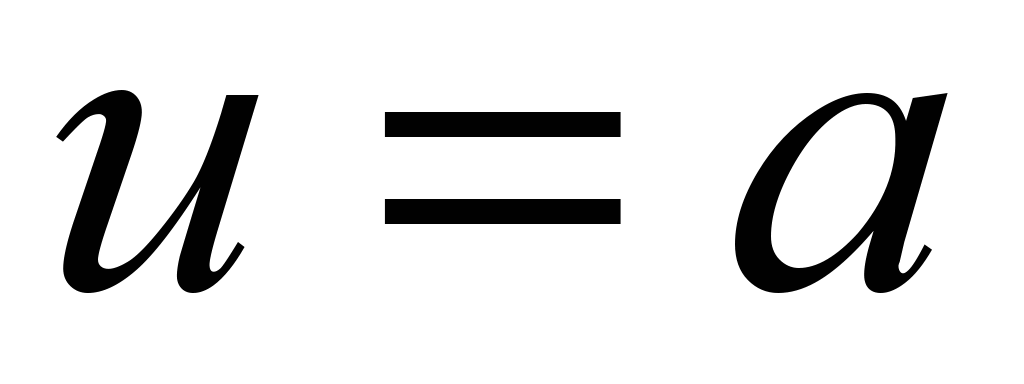
між двома точками.

Рішення. Оскільки на гвинтовій лінії
, то. Знайдемо в точці
першу квадратичну форму. Позначивши таv = t , отримаємо рівняння даної гвинтової лінії у вигляді. Квадратична форма:

= - Перша квадратична форма.

Тут. У формулі (4.15) у цьому випадку
та довжина дуги:

=

4.4 ДРУГА КВАДРАТИЧНА ФОРМА ПОВЕРХНІ.

Позначимо
‑ одиничний вектор нормалі до поверхні
:

(4.18) . (4.23)

Лінія лежить на поверхні називається лінією кривизни, якщо її напрям у кожній точці є головним напрямом.

4.6 ПОНЯТТЯ ПРО ГЕОДЕЗИЧНІ ЛІНІЇ НА ПОВЕРХНІ.

Визначення 4.1 . Крива на поверхні називається геодезичною, якщо її головна нормаль у кожній точці, де кривизна відмінна від нуля, збігається з нормаллю до поверхні.

Через кожну точку поверхні в будь-якому напрямку проходить, і при цьому лише одна геодезична. На сфері, наприклад, геодезичними є великі кола.

Параметризація поверхні називається напівгеодезичною, якщо одне сімейство координатних ліній складається з геодезичних, а друге йому ортогонально. Наприклад, на сфері меридіани (геодезичні) та паралелі.

Геодезична на досить малому відрізку є найкоротшою серед усіх близьких до неї кривих, що з'єднують самі точки.