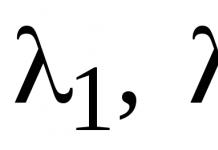Все люди от природы стремятся к знанию. (Аристотель. Метафизика)

Численные методы: решение нелинейных уравнений

Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.

В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.

В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.

Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.

В простейшем случае у нас имеется функция , заданная на отрезке (a , b ) и принимающая определенные значения.

Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.

Нам нужно найти такое значение при котором такие называются корнями функции

Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.

Метод деления пополам

Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия .

Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.

Алгоритм состоит в следующем.

Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .

Поделим отрезок пополам и введем среднюю точку .

Тогда либо , либо .

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.

Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.

Заметьте, описанный алгоритм применим для любой непрерывной функции.

К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.

Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.

Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.

Метод Ньютона: теоретические основы

Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .

Уравнение касательной к функции в точке имеет вид:

В уравнении касательной положим и .

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:

Сходимость метода касательных квадратичная, порядок сходимости равен 2.

Таким образом, сходимость метода касательных Ньютона очень быстрая.

Запомните этот замечательный факт!

Без всяких изменений метод обобщается на комплексный случай.

Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.

Упражнение 1 . Найти с помощью метода касательных решение уравнения на отрезке (0, 2).

Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).

К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.

Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.

Визуализация метода Ньютона

Метод Ньютона (метод касательных) применяется в том случае, если уравнение f (x ) = 0 имеет корень , и выполняются условия:

1) функция y = f (x ) определена и непрерывна при ;

2) f (a )· f (b ) < 0 (функция принимает значения разных знаков на концах отрезка [a ; b ]);

3) производные f" (x ) и f"" (x ) сохраняют знак на отрезке [a ; b ] (т.е. функция f (x ) либо возрастает, либо убывает на отрезке [a ; b ], сохраняя при этом направление выпуклости);

Основная идея метода заключается в следующем: на отрезке [a ; b ] выбирается такое число x 0 , при котором f (x 0 ) имеет тот же знак, что и f "" (x 0 ), т. е. выполняется условие f (x 0 )· f "" (x ) > 0 . Таким образом, выбирается точка с абсциссой x 0 , в которой касательная к кривой y = f (x ) на отрезке [a ; b ] пересекает ось Ox . За точку x 0 сначала удобно выбирать один из концов отрезка.

Рассмотрим метод Ньютона на конкретном примере.

Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f " (x) = 2 x > 0 и f "" (x) = 2 > 0 .

Рисунок 1 . f(x) =x 2 -2

Уравнение касательной в общем виде имеет представление:

y-y 0 = f " (x 0)·(x-x 0).

В нашем случае: y-y 0 =2x 0 ·(x-x 0). В качестве точки x 0 выбираем точку B 1 (b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B 1 , и обозначаем точку пересечения касательной и оси Ox точкой x 1 . Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.

Ox: x 1 =

Рисунок 2. Результат первой итерации

y=f(x) Ox через точку x 1 , получаем точку В 2 =(1.5; 0.25) . Снова проводим касательную к функции y = f(x) в точке В 2 , и обозначаем точку пересечения касательной и оси Ox точкой x 2 .

Уравнение второй касательной: y -0.25=2*1.5(x -1.5), y = 3 x - 4.25.

Точка пересечения касательной и оси Ox: x 2 = .

Рисунок 3. Вторая итерация метода Ньютона

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x 2 , получаем точку В 3 и так далее.

Рисунок 4. Третий шаг метода касательных

Первое приближение корня определяется по формуле:

= 1.5.

Второе приближение корня определяется по формуле:

=

Третье приближение корня определяется по формуле:

Таким образом, i -ое приближение корня определяется по формуле:

Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e - до выполнения неравенства | xi - xi -1 | < e .

В нашем случае, сравним приближение, полученное на третьем шаге с реальным ответом, посчитанном на калькуляторе:

Рисунок 5. Корень из 2, посчитанный на калькуляторе

Как видно, уже на третьем шаге мы получили погрешность меньше 0.000002.

Таким образом можно вычислить значение величины "корень квадратный из 2" с любой степенью точности. Этот замечательный метод был изобретен Ньютоном и позволяет находить корни очень сложных уравнений.

Метод Ньютона: приложение на С++

В данной статье мы автоматизируем процесс вычисления корней уравнений, написав консольное приложение на языке C++. Разрабатывать его мы будем в Visual C++ 2010 Express, это бесплатная и очень удобная среда разработки С++.

Для начала запустим Visual C++ 2010 Express. Появится стартовое окно программы. В левом углу нажмем «Создать проект».

Рис. 1. Начальная страница Visual C++ 2010 Express

В появившемся меню выберем «Консольное приложение Win32», введем имя приложение «Метод_Ньютона».

Рис. 2. Создание проекта

// Метод_Ньютона.cpp: определяет точку входа для консольного приложения #include "stdafx.h" #include using namespace std; float f(double x) //возвращает значение функции f(x) = x^2-2 float df(float x) //возвращает значение производной float d2f(float x) // значение второй производной int _tmain(int argc, _TCHAR* argv) int exit = 0, i=0;//переменные для выхода и цикла double x0,xn;// вычисляемые приближения для корня double a, b, eps;// границы отрезка и необходимая точность cout<<"Please input \n=>"; cin>>a>>b; // вводим границы отрезка, на котором будем искать корень cout<<"\nPlease input epsilon\n=>"; cin>>eps; // вводим нужную точность вычислений if (a > b) // если пользователь перепутал границы отрезка, меняем их местами if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня cout<<"\nError! No roots in this interval\n"; if (f(a)*d2f(a)>0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ? xn = x0-f(x0)/df(x0); // считаем первое приближение cout<<++i<<"-th iteration = "< while(fabs(x0-xn) > eps) // пока не достигнем необходимой точности, будет продолжать вычислять xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона cout<<++i<<"-th iteration = "< cout<<"\nRoot = "< cout<<"\nExit?=>"; } while (exit!=1); // пока пользователь не ввел exit = 1

Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.

Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.

Рис. 4. Решение ошибки компиляции проекта

Мы будем искать корни у функции f(x) = x2-2 .

Сначала проверим работу приложения на «неправильных» входных данных. На отрезке нет корней, наша программа должна выдать сообщение об ошибке.

У нас появилось окно приложения:

Рис. 5. Ввод входных данных

Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.

Рис. 6. Ошибка «На этом отрезке корней нет!»

Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».

Теперь проверим работу приложения на корректных входных данных. Введем отрезок и точность 0.0001.

Рис. 7. Вычисление корня с необходимой точностью

Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.

Чтобы выйти из приложения, введем «Exit?» => 1.

Метод секущих

Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

Итерационный процесс имеет вид:

Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.

Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .

Эта замечательная величина называется золотым сечением:

Убедимся в этом, считая для удобства, что .

Таким образом, с точностью до бесконечно малых более высокого порядка

Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .

После подстановки имеем: и

Для сходимости необходимо, чтобы было положительным, поэтому .

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.

Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.

Такая процедура определения момента окончания итераций называется приемом Гарвика.

Метод парабол

Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .

Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .

В форме Ньютона она имеет вид:

Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.

Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.

Этот метод очень удобен для поиска корней многочленов высокой степени.

Метод простых итераций

Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.

Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).

По теореме Банаха существует и единственна неподвижная точка

Она может быть найдена как предел простой итерационной процедуры

где начальное приближение — произвольная точка промежутка .

Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа

Таким образом, если производная меньше единицы, то является сжатием.

Условие существенно, ибо если, например, на , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.

Пусть корень уравнения f(x)=0 отделен на отрезке , причем первая и вторая производные f’(x) и f""(x) непрерывны и знакопостоянны при хÎ .

Пусть на некотором шаге уточнения корня получено (выбрано) очередное приближение к корню х n . Тогда предположим, что следующее приближение, полученное с помощью поправки h n , приводит к точному значению корня

x = х n + h n . (1.2.3-6)

Считаяh n малой величиной, представим f(х n + h n) в виде ряда Тейлора, ограничиваясь линейными слагаемыми

f(х n + h n) »f(х n) + h n f’(х n). (1.2.3-7)

Учитывая, что f(x) = f(х n + h n) = 0, получим f(х n) + h n f ’(х n) » 0.

Отсюда h n » - f(х n)/ f’(х n). Подставим значение h n в (1.2.3-6) и вместо точного значения корня x получим очередное приближение

Формула (1.2.3-8) позволяет получить последовательность приближенийх 1 ,х 2 , х 3 …, которая при определенных условиях сходится к точному значению корняx, то есть

Геометрическая интерпретация метода Ньютона состоит в следующем
(рис.1.2.3-6). Примем за начальное приближение x 0 правый конец отрезка b и в соответствующей точке В 0 на графике функции y = f(x) построим касательную. Точка пересечения касательной с осью абсцисс принимается за новое более точное приближение х 1 . Многократное повторение этой процедуры позволяет получить последовательность приближений х 0 , х 1 , х 2 , . . ., которая стремится к точному значению корня x.

Расчетная формула метода Ньютона (1.2.3-8) может быть получена из геометрического построения. Так в прямоугольном треугольнике х 0 В 0 х 1 катет
х 0 х 1 = х 0 В 0 /tga. Учитывая, что точка В 0 находится на графике функции f(x), а гипотенуза образована касательной к графику f(x) в точке В 0 , получим

(1.2.3-9)

(1.2.3-10)

Эта формула совпадает с (1.2.3-8) для n-го приближения.

Из рис.1.2.3-6 видно, что выбор в качестве начального приближения точки а может привести к тому, что следующее приближение х 1 окажется вне отрезка , на котором отделен корень x . В этом случае сходимость процесса не гарантирована. В общем случае выбор начального приближения производится в соответствии со следующим правилом: за начальное приближение следует принять такую точку х 0 Î,в которой f(х 0)×f’’(х 0)>0, то есть знаки функции и ее второй производной совпадают.

Условия сходимости метода Ньютона сформулированы в следующей теореме.

Если корень уравнения отделен на отрезке , причем f’(х 0)и f’’(х) отличны от нуля и сохраняют свои знаки при хÎ , то, если выбрать в качестве начального приближения такую точку х 0 Î, что f(х 0).f¢¢(х 0)>0, то корень уравнения f(x)=0может быть вычислен с любой степенью точности.

Оценка погрешности метода Ньютона определяется следующим выражением:

(1.2.3-11)

где -- наименьшее значение при

Наибольшее значение при

Процесс вычислений прекращается, если ,

где -- заданная точность.

Кроме того, условием достижения заданной точности при уточнении корня методом Ньютона могут служить следующие выражения:

Схема алгоритма метода Ньютона приведена на рис. 1.2.3-7.

Левая часть исходного уравнения f(x) и ее производная f’(x)в алгоритме оформлены в виде отдельных программных модулей.

Рис. 1.2.3-7. Схема алгоритма метода Ньютона

Пример 1.2.3-3.Уточнить методом Ньютона корни уравнения x-ln(x+2) = 0при условии, что корни этого уравнения отделены на отрезках x 1 Î[-1.9;-1.1] и x 2 Î [-0.9;2].

Первая производная f’(x) = 1 – 1/(x+2) сохраняет свой знак на каждом из отрезков:

f’(x)<0 при хÎ [-1.9; -1.1],

f’(x)>0 при хÎ [-0.9; 2].

Вторая производная f"(x) = 1/(x+2) 2 > 0 при любых х.

Таким образом, условия сходимости выполняются. Поскольку f""(x)>0на всей области допустимых значений, то для уточнения корня за начальное приближение x 1 выберем х 0 =-1,9(так какf(-1,9)×f”(-1.9)>0). Получим последовательность приближений:

Продолжая вычисления, получим следующую последовательность первых четырех приближений: -1.9; –1.8552, -1.8421; -1.8414. Значение функции f(x) в точке x=-1.8414 равно f(-1.8414)=-0.00003.

Для уточнения корня x 2 Î[-0.9;2] выберем в качестве начального приближениях 0 =2 (f(2)×f”(2)>0). Исходя из х 0 = 2, получим последовательность приближений: 2.0;1.1817; 1.1462; 1.1461. Значение функции f(x) в точке x=1.1461 равно f(1.1461)= -0.00006.

Метод Ньютона обладает высокой скоростью сходимости, однако на каждом шаге он требует вычисления не только значения функции, но и ее производной.

Метод хорд

Геометрическая интерпретация метода хорд состоит в следующем
(рис.1.2.3-8).

Проведем отрезок прямой через точки A и B. Очередное приближение x 1 является абсциссой точки пересечения хорды с осью 0х. Построим уравнение отрезка прямой:

Положим y=0и найдем значение х=х 1 (очередное приближение):

Повторим процесс вычислений для получения очередного приближения к корню - х 2 :

В нашем случае (рис.1.2.11) и расчетная формула метода хорд будет иметь вид

Эта формула справедлива, когда за неподвижную точку принимается точка b, а в качестве начального приближения выступает точка a.

Рассмотрим другой случай (рис. 1.2.3-9), когда .

Уравнение прямой для этого случая имеет вид

Очередное приближение х 1 при y = 0

Тогда рекуррентная формула метода хорд для этого случая имеет вид

Следует отметить, что за неподвижную точку в методе хорд выбирают тот конец отрезка , для которого выполняется условие f (x)∙f¢¢ (x)>0.

Таким образом, если за неподвижную точку приняли точку а, то в качестве начального приближения выступает х 0 = b, и наоборот.

Достаточные условия, которые обеспечивают вычисление корня уравнения f(x)=0 по формуле хорд, будут теми же, что и для метода касательных (метод Ньютона), только вместо начального приближения выбирается неподвижная точка. Метод хорд является модификацией метода Ньютона. Разница состоит в том, что в качестве очередного приближения в методе Ньютона выступает точка пересечения касательной с осью 0Х,а в методе хорд – точка пересечения хорды с осью 0Х – приближения сходятся к корню с разных сторон.

Оценка погрешности метода хорд определяется выражением

(1.2.3-15)

Условие окончания процесса итераций по методу хорд

(1.2.3-16)

В случае, если M 1 <2m 1 , то для оценки погрешности метода может быть использована формула | x n -x n -1 |£e.

Пример 1.2.3-4. Уточнить корень уравнения e x – 3x = 0, отделенный на отрезке с точностью 10 -4 .

Проверим условие сходимости:

Следовательно, за неподвижную точку следует выбрать а=0, а в качестве начального приближения принять х 0 =1, поскольку f(0)=1>0 и f(0)*f"(0)>0.

В задаче минимизации функции первостепенное значение имеет удачный выбор начального приближения Разумеется, невозможно придумать общего правила, которое было бы удовлетворительно для всех случаев, т. е. для всех возможных нелинейных функций Каждый раз приходится искать свое решение. Ниже предлагается набор некоторых способов нахождения грубых начальных приближений, который на практике может служить отправной точкой поиска удовлетворительных приближений в конкретной задаче.

9.6.1. Поиск на сетке. Особенно эффективен этот метод при небольшом числе собственно нелинейных параметров. Часто функции устроены так, что при фиксации значений одних параметров (которые и называем собственно нелинейными) остальная часть параметров становится линейной.

Задаваясь тогда нижней и верхней границей для нелинейных параметров, с некоторым шагом можно устроить перебор вариантов на полученной сетке значений этих собственно нелинейных параметров и выявить ту линейную регрессию, которая приводит к минимальной сумме квадратов.

В качестве примера рассмотрим функцию

Здесь собственно нелинейным параметром будет . Допустим, известно, что . Пусть h - шаг для параметра . Вычислим линейных регрессий

где и найдем для каждой из них минимальную сумму квадратов. Наименьшей из них соответствует оптимальное начальное приближение. В принципе шаг , от которого зависит «густота» сетки, может варьироваться, так что за счет уменьшения величины h значения параметров могут быть найдены с любой точностью.

9.6.2. Преобразование модели.

Иногда некоторым преобразованием модель можно свести к линейной или же уменьшить число собственно нелинейных параметров (см. п. 6.2.3). Покажем, как этого можно добиться, на примере логистической кривой

Производя над соответствующими уравнениями регрессии обратное преобразование, получим

Обозначая приходим к новой функции, число линейных параметров которой увеличилось с одного до двух . Оценка для параметра в новой модели может быть найдена, например, по предыдущему методу.

Здесь уместно сделать следующее замечание о преобразованиях регрессионных моделей. Следует иметь в виду, что ошибка , входившая аддитивно в исходное уравнение, после преобразования, вообще говоря, уже не будет аддитивна.

Пользуясь разложением в ряд Тейлора и обозначая преобразование через получим, пренебрегая слагаемыми порядка

Отсюда следует, что

Последнее равенство можно взять за основу для анализа задачи с преобразованной моделью.

9.6.3. Разбиение выборки на подвыборки.

Для нахождения начального приближения можно разбить всю выборку на подвыборок (с приблизительно равными объемамй), где - число неизвестных параметров. Для каждой подвыборки найдем средние по у и по X, которые обозначим соответственно т. Решим систему нелинейных уравнений относительно

Решение этой системы и будет являться начальным приближением параметров. Очевидно, для того чтобы данный метод «работал», необходимо, чтобы эта система нелинейных уравнений решалась довольно легко, например аналитически.

9.6.4. Разложение в ряд Тейлора по независимым переменным.

Основой итеративной минимизации суммы квадратов является разложение функции регрессии в ряд Тейлора до линейных членов по параметрам. Для нахождения грубого начального приближения иногда бывает полезна процедура аппроксимации регрессии путем разложения ее в ряд Тейлора по независимым переменным . Будем для простоты считать одномерным. Пусть - среднее значение, тогда приближенно

Обозначим , таким образом приходим к линейной модели

Пусть - мнк-оценки параметров этой линейной регрессии. В качестве начальных приближений примем решение нелинейной системы уравнений относительно

Мучаясь в школе над решением уравнений на уроках математики, многие ученики часто уверены, что тратят время абсолютно впустую, а между тем такой навык пригодится в жизни не только тем, кто решит пойти по стопам Декарта, Эйлера или Лобачевского.

На практике, например в медицине или экономике, сплошь и рядом встречаются ситуации, когда специалисту требуется выяснить, когда концентрация активного вещества того или иного препарата достигнет требуемого уровня в крови пациента или нужно высчитать время, необходимое конкретному бизнесу для того, чтобы он стал рентабельным.

Чаще всего речь идет о решении нелинейных уравнений различного типа. Сделать это максимально быстро, особенно с использованием ЭВМ, позволяют численные методы. Они хорошо изучены и давно доказали свою эффективность. К их числу относится и метод касательных Ньютона, которым посвящена эта статья.

Постановка задачи

В данном случае имеется функция g, которая задана на отрезке (a, b) и принимает на нем определенные значения, т. е. каждому x, принадлежащему (a, b) возможно сопоставить конкретное число g(x).

Требуется установить все корни уравнения из промежутка между точками a и b (включая концы), для которых функция обнуляется. Очевидно, что это будут точки пересечения y = g(x) с ОХ.

В некоторых случаях удобнее заменить g(x)=0 на аналогичное, вида g 1 (x) = g 2 (x). В таком случае в качестве корней выступают абсциссы (значение x) точек пересечения графиков g 1 (x) и g 2 (x).

Решение нелинейного уравнения важно и для задач оптимизации, для которых условие локального экстремума - обращение в 0 производной функции. Иными словами, такая задача может свестись к поиску корней уравнения p(x) = 0, где p(x) тождественна g"(x).

Методы решения

Для некоторых видов нелинейных уравнений, например квадратных или простых тригонометрических, найти корни можно достаточно простыми способами. В частности, каждый школьник знает формулы, используя которые можно без проблем находить значения аргумента точек, где обнуляется квадратный трехчлен.

Способы извлечения корней нелинейных уравнений принято делить на аналитические (прямые) и итерационные. В первом случае искомое решение имеет вид формулы, используя которую за некоторое число арифметических операций можно найти значение искомых корней. Подобные методы разработаны для показательных, тригонометрических, логарифмических и простейших алгебраических уравнений. Для остальных же приходится использовать специальные численные методы. Их легко реализовать с помощью ЭВМ, которые позволяют найти корни с требуемой точностью.

К их числу относится и так называемый численный метод касательных.Последний был предложен великим ученым Исааком Ньютоном в конце XVII века. В последующие столетия метод неоднократно совершенствовался.

Локализация

Численные способы решения сложных уравнений, не имеющих аналитических решений, принято осуществлять в 2 этапа. Сначала требуется их локализировать. Эта операция заключается в нахождение таких отрезков на ОХ, на которых существует один корень решаемого уравнения.

Рассмотрим отрезок . Если g(x) на нем не имеет разрывов и принимает в концевых точках значения разных знаков, то между a и b или в них самих расположен по крайней мере 1 корень уравнения g(x) = 0. Чтобы он был единственным, требуется, чтобы g(x) на была монотонной. Как известно, таким свойством она будет обладать при условии знакопостоянства g’(x).

Говоря иначе, если на g(x) не имеет разрывов и монотонно растет или убывает, а ее значения в концевых точках имеют не одинаковые знаки, то на существует 1 и только 1 корень g(x).

При этом следует знать, что этот критерий не будет действовать для корней уравнений, являющихся кратными.

Решение уравнения делением пополам

Прежде чем рассматривать более сложные численные касательныхи его разновидности) стоит познакомиться с наиболее простым способом выявления корней. Он называется дихотомией и относится к интуитивным нахождения корней основан на теореме о том, что если для g(x), непрерывной на выполняется условие разнознаковости, то на рассматриваемом отрезке есть хотя бы 1 корень g(x) = 0.

Для его обнаружения нужно поделить отрезок пополам и обозначить среднюю точку как x 2 . Тогда возможны два варианта: g(x 0) * g(x 2) либо g(x 2) * g(x 1) равны или меньше 0. Выбираем тот, для которого верно одно из этих неравенств. Повторяем процедуру, описанную выше, пока длина не станет меньше некой, заранее выбранной величины, определяющей точность определения корня уравнения на .

К достоинствам метода относится его надежность и простота, а недостаток — необходимость изначально выявить точки, в которых g(x) принимает разные знаки, поэтому его нельзя применять для корней, обладающих четной кратностью. Кроме того, он не обобщается на случай системы уравнений или если речь идет о комплексных корнях.

Пример 1

Пусть мы хотим решить уравнение g(x) = 2x 5 + x - 1 = 0. Чтобы долго не искать подходящий отрезок, строим график, используя, например, известную программу "Эксель". Мы видим, что в качестве отрезка для локализации корня лучше брать значения из промежутка . Мы можем быть уверены, что хотя бы один корень искомого уравнения на нем есть.

g"(x) = 10x 4 + 1, т. е. это монотонно возрастающая функция, поэтому на выбранном отрезке есть только 1 корень.

Подставляем концевые точки в уравнение. Имеем 0 и 1 соответственно. На первом шаге за решение берем точку 0,5. Тогда g(0,5) = -0,4375. Значит,следующий отрезок для деления пополам будет . Его серединная точка - 0,75. В ней значение функции равно 0,226. Берем для рассмотрения отрезок и его середину, которая находится в точке 0,625. Вычисляем значение g(x) в 0,625. Оно равно -0,11, т. е. отрицательное. Опираясь на этот результат, выбираем отрезок . Получаем x = 0,6875. Тогда g(x) = -0,00532. Если точность решения 0,01, то можем считать, что искомый результат равен 0,6875.

Теоретическая база

Этот способ нахождения корней методом касательных Ньютона пользуется популярностью из-за его очень быстрой сходимости.

Он основан на том доказанном факте, что если x n — приближение к корню f(x)=0, таком, что f" C 1 , то следующая апроксимация будет в точке, где обнуляется уравнение касательной к f(x), т. е.

Подставляем x = x n+1 и обнуляем y.

Тогда касательных выглядит так:

Пример 2

Попробуем использовать классический метод касательных Ньютона и найти решение какого-либо нелинейного уравнения, которое сложно или невозможно отыскать аналитически.

Пусть требуется выявить корни для x 3 + 4x - 3 = 0 с некоторой точностью, например 0,001. Как известно, график любой функции в виде многочлена нечетной степени должен хотя бы раз пересекать ось ОХ, т. е. сомневаться в существовании корней не приходится.

Прежде чем решить наш пример методом касательных, строим графикf(x) = x 3 + 4x - 3 поточечно. Это очень легко сделать, например, используя табличный процессор "Эксель". Из полученного графика будет видно, что на происходит его пересечение с осью ОХ и функция y = x 3 + 4x - 3 монотонно возрастает. Мы можем быть уверены, что на уравнения x 3 + 4x - 3 = 0 имеет решение и оно единственное.

Алгоритм

Любое решение уравнений методом касательных начинается с вычисления f "(x). Имеем:

Тогда вторая производная будет иметь вид x * 6.

Используя эти выражения, можем записать формулу для выявления корней уравнения по методу касательных в виде:

Далее требуется выбрать начальное приближение, т. е. заняться определением, какую точку считать стартовой (об. x 0) для итерационного процесса. Рассматриваем концы отрезка . Нам подойдет тот, для которого верно условие разнознаковости функции и ее 2-ой производной в x 0 . Как видим, при подстановке x 0 = 0 оно нарушено, а вот x 0 = 1 вполне подходит.

то если нас интересует решение методом касательных с точностью e, то значение x n можно считать удовлетворяющим требованиям задачи, при условии выполнения неравенства|f(x n) / f’(x n)|< e.

На первом шаге касательных имеем:

• x 1 = x 0 - (x 0 3 + 4x 0 - 3) / (3x 0 2 + 4) = 1- 0,2857 = 0,71429;
• так как условие не выполняется, идем далее;
• получаем новое значение для x 2 , которое равно 0,674;
• замечаем, что отношение значения функции к ее производной в x 2 меньше 0,0063, прекращаем процесс.

Метод касательных в Excel

Решить предыдущий пример можно намного легче и быстрее, если не производить расчеты вручную (на калькуляторе), а использовать возможности табличного процессора от компании "Майкрософт".

Для этого в "Эксель" нужно создать новую страницу и заполнить ее ячейки следующими формулами:

• в C7 записываем «= СТЕПЕНЬ (B7;3) + 4 * B7 - 3»;
• в D7 вписываем «= 4 + 3 * СТЕПЕНЬ (B7;2)»;
• в E7 записываем «= (СТЕПЕНЬ (B7;3)- 3 + 4 * B7) / (3* СТЕПЕНЬ (B7;2) + 4)»;
• в D7 вписываем выражение «=В7 - Е7»;
• в B8 вписываем формулу-условие «= ЕСЛИ(Е7 < 0,001;"Завершение итераций"; D7)».

В конкретной задаче уже в ячейке B10 появится надпись «Завершение итераций», и за решение задачи нужно будет взять число, записанное в ячейке, расположенной на одну строку выше. Для него можно выделить и отдельный «растягиваемый» столбец, введя там формулу-условие, согласно которой там будет записан результат, если содержимое в той или иной ячейке столбца B примет вид «Завершение итераций».

Реализация в Pascal

Попробуем получить решение нелинейного уравнения y = х 4 - 4 - 2 * х методом касательных в Паскале.

Используем вспомогательную функцию, которая поможет осуществить приближенное вычисление f"(x) = (f(x + delta) - f(x)) / delta. В качестве условия для завершения итерационного процесса выберем выполнение неравенства|x 0 -x 1 |< некого малого числа. В Паскале его запишем, как abs(x0 - x1)<= epsilon.

Программа примечательна тем, что не требует ручного вычисления производной.

Метод хорд

Рассмотрим еще один способ выявления корней нелинейных уравнений. Процесс итераций заключается в том, что в качестве последовательных приближений к искомому корню для f(x)=0 принимают значения точек пересечения хорды с абсциссами концевых точек a и b с ОХ, обозначаемые, как х 1 , ..., х n . Имеем:

Для точки, где хорда пересекается с осью ОХ выражение запишется, как:

Пусть вторая производная положительная при х £ (противоположный случай сведется к рассматриваемому, если записать- f(x) = 0). В таком случае график у = f(x) - кривая, выпуклая внизу и расположенная ниже хорды AB . Могут иметь место 2 случая: когда функция имеет положительное значение в точке a или она отрицательное в точке b.

В первом случае в качестве неподвижного выбираем конец a, а за x 0 берем точку b. Тогда последовательные приближения по формуле, представленной выше, образуют последовательность, которая монотонно убывает.

Во втором случае неподвижным является конец b при x 0 = a. Значения х, полученные на каждом шаге итерации, образуют последовательность, которая монотонно возрастает.

Таким образом, можем констатировать, что:

• неподвижным в методе хорд является тот конец отрезка, где не совпадают знаки функции и ее второй производной;
• приближения для корня x — x m — лежат от него в той стороне, где у f(х) знак, не совпадающий со знаком f"" (х).

Итерации можно продолжать, пока не выполнится условия близости корней на этом и предыдущем итерационном шаге по модулю abs(x m - x m - 1)< e.

Модифицированный способ

Комбинированный метод хорд и касательныхпозволяет устанавливать корни уравнения, приближаясь к ним с разных сторон. Такое значение, при котором график f(x) пересекает OX, позволяет уточнить решение гораздо быстрее, чем по каждому из методов по отдельности.

Предположим, нужно отыскать корни f(x)=0, если они есть на . Можно применить любой из описанных выше способов. Однако лучше попробовать их комбинацию, благодаря чему значительно повысится точность корня.

Рассматриваем случай с начальным приближением, соответствующим условию разнознаковости первой и второй производной в конкретной точке х.

В таких условиях решение нелинейных уравнений методом касательных позволяет найти корень с избытком, если x 0 =b, а способ с использованием хорд при неподвижном конце b приводит к нахождению приближенного корня с недостатком.

Используются формулы:

Теперь искомый корень х нужно искать в интервале. На следующем шаге нужно применить комбинированный метод уже к этому отрезку. Действуя так далее, получим формулы вида:

Если же имеет место разнознаковость первой и второй производных, то, рассуждая аналогичным образом, для уточнения корня получим следующие рекурентные формулы:

В качестве условия используется оценочное неравенство| b n +1 - a n +1 |< e. Иными словами, на практике приходится находить решение при помощи двух методов, но на каждом шаге требуется выяснять, насколько полученные результаты близки друг другу.

Если вышеприведенное неравенство верно, то в качестве корня нелинейного уравнения на заданном отрезке берут точку, которая находится ровно посередине между найденными решениями на конкретном итерационном шаге.

Комбинированный метод легко реализуется в среде TURBO PASCAL. При большом желании можно попробовать осуществить все вычисления табличным методом в программе "Эксель".

В последнем случае выделяют по нескольку столбцов для решения задачи с использованием хорд и отдельно для способа, предложенного Исааком Ньютоном.

При этом каждая строка используется для записи вычислений на конкретном итерационном шаге по двум методам. Затем, в левой части от области решения, на активной рабочей странице выделяется столбец, в котором вписывается результат вычислений модуля разности значений очередного итерационного шага по каждому из методов. Еще один можно использовать для внесения результатов вычислений по формуле расчета логической конструкции «ЕСЛИ», используемой для выяснения, выполняется ли условие или нет.

Теперь вы знаете, как решать сложные уравнения. Метод касательных,как вы уже видели, реализуется достаточно просто, как в Паскале, так и в "Экселе". Поэтому вы всегда сможете установить корни уравнения, которое сложно или невозможно решить посредством формул.