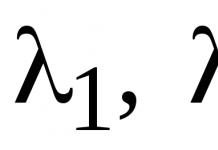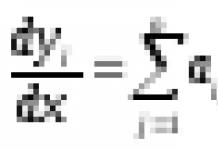Введение

квадратичная форма канонический вид уравнение

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнениями второго порядка, содержащими две или три переменные. Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Теория квадратичных форм впервые была развита французским математиком Лагранжем, которому принадлежат многие идеи в этой теории, в частности, он ввел важное понятие приведенной формы, с помощью которого им была доказана конечность числа классов бинарных квадратичных форм заданного дискриминанта. Затем эта теория значительно была расширенна Гауссом, который ввел много новых понятий, на основе которых ему удалось получить доказательства трудных и глубоких теорем теории чисел, ускользавших от его предшественников в этой области.

Целью работы является изучение видов квадратичных форм и способов приведения квадратичных форм к каноническому виду.

В данной работе поставлены следующие задачи: выбрать необходимую литературу, рассмотреть определения и основные теоремы, решить ряд задач по данной теме.

Приведение квадратичной формы к каноническому виду

Истоки теории квадратичных форм лежат в аналитической геометрии, а именно в теории кривых (и поверхностей) второго порядка. Известно, что уравнение центральной кривой второго порядка на плоскости, после перенесения начала прямоугольных координат в центр этой кривой, имеет вид

что в новых координатах уравнение нашей кривой будет иметь «канонический» вид

в этом уравнении коэффициент при произведении неизвестных равен, следовательно, нулю. Преобразование координат (2) можно толковать, очевидно, как линейное преобразование неизвестных, притом невырожденное, так как определитель из его коэффициентов равен единице. Это преобразование применяется к левой части уравнения (1), и поэтому можно сказать, что левая часть уравнения (1) невырожденным линейным преобразованием (2) превращается в левую часть уравнения (3).

Многочисленные приложения потребовали построения аналогичной теории для случая, когда число неизвестных вместо двух равно любому, а коэффициенты являются или действительными, или же любыми комплексными числами.

Обобщая выражение, стоящее в левой части уравнения (1), мы приходим к следующему понятию.

Квадратичной формой от неизвестных называется сумма, каждый член которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты действительными или же могут быть любыми комплексными числами.

Считая, что в квадратичной форме уже сделано приведение подобных членов, введем следующие обозначения для коэффициентов этой формы: коэффициент при обозначим через, а коэффициент при произведении для - через (сравнить с (1)!).

Так как, однако, то коэффициент при этом произведении мог бы быть обозначен и через, т.е. введенные нами обозначения предполагают справедливость равенства

Член можно записать теперь в виде

а всю квадратичную форму - в виде суммы всевозможных членов, где и уже независимо друг от друга принимают значения от 1 до:

в частности, при получается член

Из коэффициентов можно составить, очевидно, квадратную матрицу порядка; она называется матрицей квадратичной формы, а ее ранг - рангом этой квадратичной формы.

Если, в частности, т.е. матрица - невырожденная, то и квадратичная форма называется невырожденной. Ввиду равенства (4) элементы матрицы А, симметричные относительно главной диагонали, равны между собой, т.е. матрица А - симметрическая. Обратно, для любой симметрической матрицы А порядка можно указать вполне определенную квадратичную форму (5) от неизвестных, имеющую элементы матрицы А своими коэффициентами.

Квадратичную форму (5) можно записать в ином виде, используя умножение прямоугольных матриц. Условимся сначала о следующем обозначении: если дана квадратная или вообще прямоугольная матрица А, то через будет обозначаться матрица, полученная из матрицы А транспонированием. Если матрицы А и В таковы, что их произведение определено, то имеет место равенство:

т.е. матрица, полученная транспонированием произведения, равна произведению матриц, получающихся транспонированием сомножителей, притом взятых в обратном порядке.

В самом деле, если произведение АВ определено, то будет определено, как легко проверить, и произведение: число столбцов матрицы равно числу строк матрицы. Элемент матрицы, стоящий в ее й строке и м столбце, в матрице АВ расположен в й строке и м столбце. Он равен поэтому сумме произведений соответственных элементов й строки матрицы А и го столбца матрицы В, т.е. равен сумме произведений соответственных элементов го столбца матрицы и й строки матрицы. Этим равенство (6) доказано.

Заметим, что матрица А тогда и только тогда будет симметрической, если она совпадает со своей транспонированной, т.е. если

Обозначим теперь через столбец, составленный из неизвестных.

является матрицей, имеющей строк и один столбец. Транспонируя эту матрицу, получим матрицу

Составленную из одной строки.

Квадратичная форма (5) с матрицей может быть записана теперь в виде следующего произведения:

Действительно, произведение будет матрицей, состоящей из одного столбца:

Умножая эту матрицу слева на матрицу, мы получим «матрицу», состоящую из одной строки и одного столбца, а именно правую часть равенства (5).

Что произойдет с квадратичной формой, если входящие в нее неизвестные будут подвергнуты линейному преобразованию

Отсюда по (6)

Подставляя (9) и (10) в запись (7) формы, получаем:

Матрица В будет симметрической, так как ввиду равенства (6), справедливого, очевидно, для любого числа множителей, и равенства равносильного симметричности матрицы, имеем:

Таким образом, доказана следующая теорема:

Квадратичная форма от неизвестных, имеющая матрицу, после выполнения линейного преобразования неизвестных с матрицей превращается в квадратичную форму от новых неизвестных, причем матрицей этой формы служит произведение.

Предположим теперь, что мы выполняем невырожденное линейное преобразование, т.е. , а поэтому и - матрицы невырожденные. Произведение получается в этом случае умножением матрицы на невырожденные матрицы и поэтому, ранг этого произведения равен рангу матрицы. Таким образом, ранг квадратичной формы не меняется при выполнении невырожденного линейного преобразования.

Рассмотрим теперь, по аналогии с указанной в начале параграфа геометрической задачей приведения уравнения центральной кривой второго порядка к каноническому виду (3), вопрос о приведении произвольной квадратичной формы некоторым невырожденным линейным преобразованием к виду суммы квадратов неизвестных, т.е. к такому виду, когда все коэффициенты при произведениях различных неизвестных равны нулю; этот специальный вид квадратичной формы называется каноническим. Предположим сначала, что квадратичная форма от неизвестных уже приведена невырожденным линейным преобразованием к каноническому виду

где - новые неизвестные. Некоторые из коэффициентов могут. Конечно, быть нулями. Докажем, что число отличных от нуля коэффициентов в (11) непременно равно рангу формы.

В самом деле, так как мы пришли к (11) при помощи невырожденного преобразования, то квадратичная форма, стоящая в правой части равенства (11), также должна быть ранга.

Однако матрица этой квадратичной формы имеет диагональный вид

и требование, чтобы эта матрица имела ранг, равносильно предположению, что на ее главной диагонали стоит ровно отличных от нуля элементов.

Перейдем к доказательству следующей основной теоремы о квадратичных формах.

Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду. Если при этом рассматривается действительная квадратичная форма, то все коэффициенты указанного линейного преобразования можно считать действительными.

Эта теорема верна для случая квадратичных форм от одного неизвестного, так как всякая такая форма имеет вид, являющийся каноническим. Мы можем, следовательно, вест доказательство индукцией по числу неизвестных, т.е. доказывать теорему для квадратичных форм от n неизвестных, считая ее уже доказанной для форм с меньшим числом неизвестных.

Пуст дана квадратичная форма

от n неизвестных. Мы постараемся найти такое невырожденное линейное преобразование, которое выделило бы из квадрат одного из неизвестных, т.е. привело бы к виду суммы этого квадрата и некоторой квадратичной формы от остальных неизвестных. Эта цель легко достигается в том случае, если среди коэффициентов стоящих в матрице формы на главной диагонали, есть отличные от нуля, т.е. если в (12) входит с отличием от нуля коэффициентов квадрат хотя бы одного из неизвестных

Пусть, например, . Тогда, как легко проверить, выражение, являющееся квадратичной формой, содержит такие же члены с неизвестным, как и наша форма, а поэтому разность

будет квадратичной формой, содержащей лишь неизвестные, но не. Отсюда

Если мы введем обозначения

то получим

где будет теперь квадратичной формой о неизвестных. Выражение (14) есть искомое выражение для формы, так как оно получено из (12) невырожденным линейным преобразованием, а именно преобразованием, обратным линейному преобразованию (13), которое имеет своим определителем и поэтому не вырождено.

Если же имеют место равенства то предварительно нужно совершить вспомогательное линейное преобразование, приводящее к появлению в нашей форме квадратов неизвестных. Так как среди коэффициентов в записи (12) этой формы должны быть отличные от нуля, - иначе нечего было бы доказывать, - то пусть, например, т.е. является суммой члена и членов, в каждый из которых входит хотя бы одно из неизвестных.

Совершим теперь линейное преобразование

Оно будет невырожденным, так как имеет определитель

В результате этого преобразования член нашей формы примет вид

т.е. в форме появятся, с отличными от нуля коэффициентами, квадраты сразу двух неизвестных, причем они не могут сократиться ни с одним из остальных членов, так как в каждый их этих последних входит хотя бы одно из неизвестных теперь мы находимся в условиях уже рассмотренного выше случая, т.е. еще одним невырожденным линейным преобразованием можем привести форму к виду (14).

Для окончания доказательства остается отметить, что квадратичная форма зависит от меньшего, чем, числа неизвестных и поэтому, по предположению индукции, некоторым невырожденным преобразованием неизвестных приводится к каноническому виду. Это преобразование, рассматриваемое как (невырожденное, как легко видеть) преобразование всех неизвестных, при котором остается без изменения, приводит, следовательно, (14) к каноническому виду. Таким образом, квадратичная форма двумя или тремя невырожденными линейными преобразованиями, которые можно заменить одним невырожденным преобразованием - их произведением, приводится к виду суммы квадратов неизвестных с некоторыми коэффициентами. Число этих квадратов равно, как мы знаем, рангу формы. Если, сверх того, квадратичная форма действительная, то коэффициенты как в каноническом виде формы, так и в линейном преобразовании, приводящем к этому виду, будут действительными; в самом деле, и линейное преобразование, обратное (13), и линейное преобразование (15) имеют действительные коэффициенты.

Доказательство основной теоремы закончено. Метод, использованный в этом доказательстве, может быть применен в конкретных примерах для действительного приведения квадратичной формы к каноническому виду. Нужно лишь вместо индукции, которую мы использовали в доказательстве, последовательно выделять изложенным выше методом квадраты неизвестных.

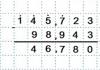
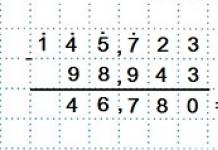
Пример 1. Привести к каноническому виду квадратичную форму

Ввиду отсутствия в этой форме квадратов неизвестных мы выполним сначала невырожденное линейное преобразование

с матрицей

после чего получим:

Теперь коэффициенты при отличен от нуля, и поэтому из нашей формы можно выделить квадрат одного неизвестного. Полагая

т.е. совершая линейное преобразование, для которого обратное будет иметь матрицу

мы приведем к виду

Пока выделился лишь квадрат неизвестного, так как форма еще содержит произведение двух других неизвестных. Используя неравенство нулю коэффициента при, еще раз применим изложенный выше метод. Совершая линейное преобразование

для которого обратное имеет матрицу

мы приведем, наконец, форму к каноническому виду

Линейное преобразование, приводящее (16) сразу к виду (17), будет иметь своей матрицей произведение

Можно и непосредственной подстановкой проверить, что невырожденное (так как определитель равен) линейное преобразование

превращает (16) в (17).

Теория приведения квадратичной формы к каноническому виду построена по аналогии с геометрической теорией центральных кривых второго порядка, но не может считаться обобщением этой последней теории. В самом деле, в нашей теории допускается использование любых невырожденных линейных преобразований, в то время как приведение кривой второго порядка к каноническому виду достигается применением линейных преобразований весьма специального вида,

являющихся вращением плоскости. Эта геометрическая теория может быть, однако, обобщена на случай квадратичных форм от неизвестных с действительными коэффициентами. Изложение этого обобщения, называемого приведением квадратичных форм к главным осям, будет дано ниже.

Квадратичная форма называется канонической, если все т. е.

Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

1. Ортогональное преобразование пространства :

где - собственные значения матрицы A .

2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если

Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем

3. Метод Якоби (в случае, когда все главные миноры квадратичной формы отличны от нуля):

Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

В = С = 0, А ≠0 – прямая совпадает с осью Оу

А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)

2) двумя своими точками M 1 (x 1 , y 1 , z 1) и M 2 (x 2 , y 2 , z 2), тогда прямая, через них проходящая, задается уравнениями:

= ; (3.3)

3) точкой M 1 (x 1 , y 1 , z 1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

. (3.4)

Уравнения (3.4) называются каноническими уравнениями прямой .

Векторa называется направляющим вектором прямой .

Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:

x = x 1 +mt, y = y 1 + nt, z = z 1 + рt. (3.5)

Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y , приходим к уравнениям прямой впроекциях или к приведенным уравнениям прямой :

x = mz + a, y = nz + b. (3.6)

От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n 1 , n 2 ], где n 1 (A 1 , B 1 , C 1) и n 2 (A 2 , B 2 , C 2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Система равносильна системе x = x 1 , y = y 1 ; прямая параллельна оси Oz.

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0 (3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называетсяуравнением плоскости .

Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая может принадлежать и не принадлежать плоскости. Она принадлежит плоскости, если хотя бы две точки ее лежат на плоскости.

Если прямая не принадлежит плоскости, она может быть параллельной ей или пересекать ее.

Прямая параллельна плоскости, если она параллельна другой прямой, лежащей в этой плоскости.

Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей.

Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости.

В пространстве две прямые могут либо пересекаться, либо быть параллельными, либо быть скрещенными.

Параллельность отрезков прямых сохраняется в проекциях.

Если прямые пересекаются, то точки пересечения их одноимённых проекций находятся на одной линии связи.

Скрещивающиеся прямые не принадлежат одной плоскости, т.е. не пересекаются и не параллельны.

на чертеже одноименные проекции прямых, взятые отдельно, имеют признаки пересекающихся или параллельных прямых.

Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a , b и c (если a > b ) существует соотношение

a 2 - b 2 = c 2 .

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

У эллипса эксцентриситет e < 1 (так как c < a ), а его фокусы лежат на большой оси.

Уравнение гиперболы, изображенной на рисунке .

Параметры:
a, b – полуоси;
- расстояние между фокусами,
- эксцентриситет;
- асимптоты;
- директрисы.
Прямоугольник, изображенный в центре рисунка – основной прямоугольник, его диагонали есть асимптоты.

При рассмотрении евклидового пространства мы вводили определение квадратичной формы. С помощью некоторой матрицы

строится многочлен второго порядка вида

который называется квадратичной формой, порождаемой квадратной матрицей А.

Квадратичные формы тесно связаны с поверхностями второго порядка в n - мерном евклидовом пространстве. Общее уравнение таких поверхностей в нашем трехмерном евклидовом пространстве в декартовой системе координат имеет вид:

Верхняя строка - это не что иное, как квадратичная форма, если положить x 1 =x, x 2 =y, x 3 =z:

- симметричная матрица (a ij = a ji)

положим для общности, что многочлен

есть линейная форма. Тогда общее уравнение поверхности есть сумма квадратичной формы, линейной формы и некоторой постоянной.

Основной задачей теории квадратичных форм является приведение квадратичной формы к максимально простому виду с помощью невырожденного линейного преобразования переменных или, другими словами, замены базиса.

Вспомним, что при изучении поверхностей второго порядка мы приходили к выводу о том, что путем поворота осей координат можно избавиться от слагаемых, содержащих произведение xy, xz, yz или x i x j (ij). Далее, путем параллельного переноса осей координат можно избавиться от линейных слагаемых и в конечном итоге свести общее уравнение поверхности к виду:

В случае квадратичной формы приведение ее к виду

называется приведением квадратичной формы к каноническому виду.

Поворот осей координат есть не что иное, как замена одного базиса другим, или, другими словами, линейное преобразование.

Запишем квадратичную форму в матричном виде. Для этого представим ее следующим образом:

L(x,y,z) = x(a 11 x+a 12 y+a 13 z)+

Y(a 12 x+a 22 y+a 23 z)+

Z(a 13 x+a 23 y+a 33 z)

Введем матрицу - столбец

Тогда
- гдеX T =(x,y,z)

Матричная форма записи квадратичной формы. Эта формула, очевидно, справедлива и в общем случае:

Канонический вид квадратичной формы означает, очевидно, что матрица А имеет диагональный вид:

Рассмотрим некоторое линейное преобразование X = SY, где S - квадратная матрица порядка n, а матрицы - столбцы Х и У есть:

Матрица S называется матрицей линейного преобразования. Отметим попутно, что всякой матрице n-ного порядка при заданном базисе соответствует некоторый линейный оператор.

Линейное преобразование X = SY заменяет переменные x 1 , x 2 , x 3 новыми переменными y 1 , y 2 , y 3 . Тогда:

где B = S T A S

Задача приведения к каноническому виду сводится к отысканию такой матрицы перехода S, чтобы матрица В приобрела диагональный вид:

Итак, квадратичная форма с матрицей А после линейного преобразования переменных переходит в квадратичную форму от новых переменных с матрицей В .

Обратимся к линейным операторам. Каждой матрице А при заданном базисе соответствует некоторый линейный оператор А . Этот оператор имеет, очевидно, некоторую систему собственных чисел и собственных векторов. Причем, отметим, что в евклидовом пространстве система собственных векторов будет ортогональна. Мы доказывали на предыдущей лекции, что в базисе собственных векторов матрица линейного оператора имеет диагональный вид. Формула (*), как мы помним, это формула преобразования матрицы линейного оператора при смене базиса. Положим, что собственные вектора линейного оператора А с матрицей А - это вектора у 1 , y 2 , ..., y n .

А это означает, что если собственные вектора у 1 , y 2 , ..., y n взять за базис, то матрица линейного оператора в этом базисе будет диагональной

или В = S -1 А S, где S – матрица перехода от первоначального базиса {e } к базису {y }. Причем в ортонормированном базисе матрица S будет ортогональной.

Т. о. для приведения квадратичной формы к каноническому виду необходимо найти собственные числа и собственные векторы линейного оператора А, имеющего в первоначальном базисе матрицу А, которая порождает квадратичную форму, перейти к базису собственных векторов и в новой системе координат построить квадратичную форму.

Обратимся к конкретным примерам. Рассмотрим линии второго порядка.

или

С помощью поворота осей координат и последующего параллельного переноса осей это уравнение можно привести к виду (переменные и коэффициенты переобозначены х 1 = х, х 2 = у):

1)
если линия центральная, 1  0,  2  0

2)
если линия нецентральная, т. е. один из i = 0.

Напомним виды линий второго порядка. Центральные линии:

Нецентральные линии:

5) х 2 = а 2 две параллельные линии;

6) х 2 = 0 две сливающиеся прямые;

7) у 2 = 2рх парабола.

Для нас представляют интерес случаи 1), 2), 7).

Рассмотрим конкретный пример.

Привести к каноническому виду уравнение линии и построить ее:

5х 2 + 4ху + 8у 2 - 32х - 56у + 80 = 0.

Матрица квадратичной формы есть
. Характеристическое уравнение:

Его корни:

Найдем собственные векторы:

При  1 = 4:
u 1 = -2u 2 ; u 1 = 2c, u 2 = -c или g 1 = c 1 (2i – j).

При  2 = 9:
2u 1 = u 2 ; u 1 = c, u 2 = 2c или g 2 = c 2 (i +2j).

Нормируем эти векторы:

Составим матрицу линейного преобразования или матрицу перехода к базису g 1 , g 2:

- ортогональная матрица!

Формулы преобразования координат имеют вид:

или

Подставим в наше уравнение линии и получим:

Сделаем параллельный перенос осей координат. Для этого выделим полные квадраты по х 1 и у 1:

Обозначим
. Тогда уравнение приобретет вид: 4х 2 2 + 9у 2 2 = 36 или

Это эллипс с полуосями 3 и 2. Определим угол поворота осей координат и их сдвиг для того, чтобы построить эллипс в старой системе.

Построим:

Проверка: при х = 0: 8у 2 - 56у + 80 = 0 у 2 – 7у + 10 = 0. Отсюда у 1,2 = 5; 2

При у =0: 5х 2 – 32х + 80 = 0 Здесь нет корней, т. е. нет точек пересечения с осью х !

Приведение квадратичной формы к каноническому виду.

Канонический и нормальный вид квадратичной формы.

Линейные преобразования переменных.

Понятие квадратичной формы.

Квадратичные формы.

Определение: Квадратичной формой от переменных называется однородный многочлен второй степени относительно этих переменных.

Переменные можно рассматривать как аффинные координаты точки арифметического пространства А n или как координаты вектора n-мерного пространства V n . Будем обозначать квадратичную форму от переменных как.

Пример 1:

Если в квадратичной форме уже выполнено приведение подобных членов, то коэффициенты при обозначаются, а при () – . Т.о., считается, что. Квадратичную форму можно записать следующим образом:

Пример 2:

Матрица системы (1):

– называется матрицей квадратичной формы.

Пример: Матрицы квадратичных форм примера 1 имеют вид:

Матрица квадратичной формы примера 2:

Линейным преобразованием переменных называют такой переход от системы переменных к системе переменных, при котором старые переменные выражаются через новые с помощью форм:

где коэффициенты образуют невырожденную матрицу.

Если переменные рассматривать как координаты вектора в евклидовом пространстве относительно некоторого базиса, то линейное преобразование (2) можно рассматривать как переход в этом пространстве к новому базису, относительно которого этот же вектор имеет координаты.

В дальнейшем мы будем рассматривать квадратичные формы только с действительными коэффициентами. Будем считать, что и переменные принимают только действительные значения. Если в квадратичной форме (1) переменные подвергнуть линейному преобразованию (2), то получится квадратичная форма от новых переменных. В дальнейшем мы покажем, при надлежащем выборе преобразования (2) квадратичную форму (1) можно привести к виду, содержащему только квадраты новых переменных, т.е. . Такой вид квадратичной формы называется каноническим . Матрица квадратичной формы в таком случае диагональная: .

Если все коэффициенты могут принимать лишь одно из значений: -1,0,1 соответствующий вид называется нормальным .

Пример: Уравнение центральной кривой второго порядка с помощью перехода к новой системе координат

можно привести к виду: , а квадратичная форма в этом случае примет вид:

Лемма 1: Если квадратичная форма (1) не содержит квадратов переменных, то с помощью линейного преобразования ее можно привести в форму, содержащую квадрат хотя бы одной переменной.

Доказательство: По условию, квадратичная форма содержит только члены с произведениями переменных. Пусть при каких-либо различных значениях i и j отличен от нуля, т.е. – один из таких членов, входящих в квадратичную форму. Если выполнить линейное преобразование, а все остальные не менять, т.е. (определитель этого преобразования отличен от нуля), то в квадратичной форме появится даже два члена с квадратами переменных: . Эти слагаемые не могут исчезнуть при приведении подобных членов, т.к. каждый из оставшихся слагаемых содержит хотя бы одну переменную, отличную или от или от.

Пример:

Лемма 2: Если квадратная форма (1) содержит слагаемое с квадратом переменной , напримери еще хотя бы одно слагаемое с переменной , то с помощью линейного преобразования , f можно перевести в форму от переменных , имеющую вид: (2), где g – квадратичная форма, не содержащая переменной .

Доказательство: Выделим в квадратичной форме (1) сумму членов, содержащих: (3) здесь через g 1 обозначена сумма всех слагаемых, не содержащих.

Обозначим

(4), где через обозначена сумма всех слагаемых, не содержащих.

Разделим обе части (4) на и вычтем полученное равенство из (3), после приведения подобных будем иметь:

Выражение в правой части не содержит переменной и является квадратичной формой от переменных. Обозначим это выражение через g, а коэффициент через, а тогда f будет равно: . Если произвести линейное преобразование: , определитель которого отличен от нуля, то g будет квадратичной формой от переменных, и квадратичная форма f будет приведена к виду (2). Лемма доказана.

Теорема: Любая квадратичная форма может быть приведена к каноническому виду с помощью преобразования переменных.

Доказательство: Проведем индукцию по числу переменных. Квадратичная форма от имеет вид: , которое уже является каноническим. Предположим, что теорема верна для квадратичной формы от n-1 переменных и докажем, что она верна для квадратично формы от n переменных.

Если f не содержит квадратов переменных, то по лемме 1 ее можно привести к виду, содержащему квадрат хотя бы одной переменной, по лемме 2 полученную квадратичную форму можно представить в виде (2). Т.к. квадратичная форма является зависимой от n-1 переменных, то по индуктивному предположению она может быть приведена к каноническому виду с помощью линейного преобразования этих переменных к переменным, если к формулам этого перехода еще добавить формулу, то мы получим формулы линейного преобразования, которое приводит к каноническому виду квадратичную форму, содержащуюся в равенстве (2). Композиция всех рассматриваемых преобразований переменных является искомым линейным преобразованием, приводящим к каноническому виду квадратичную форму (1).

Если квадратичная форма (1) содержит квадрат какой-либо переменной, то лемму 1 применять не нужно. Приведенный способ называется методом Лагранжа .

От канонического вида, где, можно перейти к нормальному виду, где, если, и, если, с помощью преобразования:

Пример: Привести к каноническому виду методом Лагранжа квадратичную форму:

Т.к. квадратичная форма f уже содержит квадраты некоторых переменных, то лемму 1 применять не нужно.

Выделяем члены, содержащие:

3. Чтобы получить линейное преобразование, непосредственно приводящее форму f к виду (4), найдем сначала преобразования, обратные преобразованиям (2) и (3).

Теперь, с помощью этих преобразований построим их композицию:

Если подставить полученные значения (5) в (1), мы сразу же получим представление квадратичной формы в виде (4).

От канонического вида (4) с помощью преобразования

можно перейти к нормальному виду:

Линейное преобразование, приводящее квадратичную форму (1) к нормальному виду, выражается формулами:

Библиография:

1. Воеводин В.В. Линейная алгебра. СПБ.: Лань, 2008, 416 с.

2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2006, 304 с.

3.Кострикин А.И. Введение в алгебру. часть II. Основы алгебры: учебник для вузов, -М. : Физико-математическая литература, 2000, 368 с.

Лекция №26 (II семестр)

Тема: Закон инерции. Положительно определённые формы.

определяет на плоскости кривую. Группа членов называется квадратичной формой, – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
Матрица называется матрицей квадратичной формы. Здесь a 1 2 =a 2 1 . Чтобы матрицу B привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда , где λ 1 и λ 2 – собственные числа матрицы B.
В базисе из собственных векторов матрицы B квадратичная форма будет иметь канонический вид: λ 1 x 2 1 +λ 2 y 2 1 .
Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.
Канонический вид кривой второго порядка: λ 1 x 2 2 +λ 2 y 2 2 =a , причем:
а) если λ 1 >0; λ 2 >0 – эллипс, в частности, при λ 1 =λ 2 это окружность;
б) если λ 1 >0, λ 2 <0 (λ 1 <0, λ 2 >0) имеем гиперболу;
в) если λ 1 =0 либо λ 2 =0, то кривая является параболой и после поворота осей координат имеет вид λ 1 x 2 1 =ax 1 +by 1 +c (здесь λ 2 =0). Дополняя до полного квадрата, будем иметь: λ 1 x 2 2 =b 1 y 2 .

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение . Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ 1 =-2, λ 2 =8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x 1 2 -2y 1 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x 1 =1: x 1 =(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x 1 .
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
1 ,j 1).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

; . (*)

Вносим выражения x и y в исходное уравнение и, после преобразований, получаем: .
Выделяем полные квадраты : .
Проводим параллельный перенос осей координат в новое начало: , .
Если внести эти соотношения в (*) и разрешить эти равенства относительно x 2 и y 2 , то получим: , . В системе координат (0*, i 1 , j 1) данное уравнение имеет вид: .
Для построения кривой строим в старой системе координат новую: ось x 2 =0 задается в старой системе координат уравнением x-y-3=0, а ось y 2 =0 уравнением x+y-1=0. Начало новой системы координат 0 * (2,-1) является точкой пересечения этих прямых.
Для упрощения восприятия разобьем процесс построения графика на 2 этапа:
1. Переход к системе координат с осями x 2 =0, y 2 =0, заданными в старой системе координат уравнениями x-y-3=0 и x+y-1=0 соответственно.

2. Построение в полученной системе координат графика функции.

Окончательный вариант графика выглядит следующим образом (см. Решение :Скачать решение

Задание . Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение .