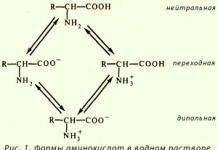
Вращательное движение твердого тела. Вращательным называется движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.

При вращательном движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой осп.

Для определения положения вращающегося тела проведем через ось г две полуплоскости: полуплоскость I - неподвижную и полуплоскость II - связанную с твердым телом и вращающуюся вместе с ним (рис. 2.4). Тогда положение тела в любой момент времени будет однозначно определяться углом j между этими полуплоскостями, взятым с соответствующим знаком, который называется углом поворота тела.

При вращении тела угол поворота j изменяется в зависимости от времени, т. е. является функцией времени t:

Это уравнение называется уравнением вращательного движения твердого тела.

Основными кинематическими характеристи­ками вращательного движения твердого тела явля­ются его угловая скорость w угловое ускорение e.

Если за время Dt = t1 + t тело совершает пово­рот на Dj = j1 –j,то средняя угловая скорость тела за этот промежуток времени будет равна

(1.16)

Для определения значения угловой скорости тела в данный момент времени t найдем предел отношения приращения угла поворота Dj к промежутку времени Dt при стремлении последнего к нулю:

(2.17)

Таким образом, угловая скорость тела в данный момент времени численно равна первой производной от угла поворота по времени. Знак угловой скорости w совпадает со знаком угла поворота тела j: w> 0 при j> 0, и наоборот, если j< 0. то и w < 0. Размерность угловой скорости обычно 1/с, так радиан величина безразмерная.

Угловую скорость можно изобразить в виде вектора w, численная величина которого равна dj/dt который направлен вдоль оси вращения тела в ту строну, откуда вращение видно происходящим против часовой стрелки.

Изменение угловой скорости тела с течением времени характеризует угловое ускорение e. По аналогии с нахождением среднего значения угловой скорости найдем выражение для определения значения среднего ускорения:

(2.18)

Тогда ускорение твердого тела в данный момент времени определится из выражения

(2.19)

т. е. угловое ускорение тела в данный момент времени равно первой произ­водной от угловой скорости или второй производной от угла поворота тела по времени. Размерность углового ускорения 1/с 2 .

Угловое ускорение твердого тела так же, как и угловая скорость, может быть представлено как вектор. Вектор углового ускорения совпадает по на­правлению с вектором угловой скорости при ускоренном движении твердого юла и направлен в противоположную сторону при замедленном движении.

Установив характеристики движения твердого тела в целом, перейдем к изучению движения отдельных его точек. Рассмотрим некоторую точку М твердого тела, находящуюся на расстоянии h от оси вращения г (рис. 2.3).

При вращении тела точка М будет описывать окружное п. радиусом h с центром на оси вращения и лежащую в плоскости, перпендикулярной этой оси. Если за время dtпроисходит элементарный попорот тела па угол dj, то точка М при этом совершает вдоль своей траектории элементарное перемещение dS = h*dj,. Тогда скорость точки М определился из выражения

(2.20)

Скорость называют линейной или окружной скоростью точки М.

Таким образом, линейная скорость точки вращающегося твердого тела численно равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Так как для всех точек тела угловая скорость w; имеет одинаковое значение, то из формулы для линейной скорости следует, что ли­нейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Линейная скорость точки твердого тела является вектором п направлена по касательной к окружности, описываемой точкой М.

Бели расстояние от оси вращения твердого пела до некоторой точки М рассматривать как радиус-вектор h точки М, то вектор линейной скорости точки v можно представить как векторное произведение вектора угловой скорости w радиус-вектор h:

V = w * h (2/21)

Действительно, результатом векторного произведения (2.21) является вектор, равный по модулю произведению w*h и направленный (рис. 2.5) перпендикулярно плоскости, в которой лежат два сомножителя, в ту сторону, откуда ближайшее совмещение первого сомножителя со вторым наблюдается происходящим против часовой стрелки, т. е. по касательной к траектории движения точки M.

Таким образом вектор, являющийся результатом векторного произведе­ния (2.21), по модулю и по направлению соответствует вектору линейной скорости точки M.

Рис. 2.5

Для нахождения выражения для ускорения а точки М выполним дифференцирование по времени выражения (2.21) для скорости точки

(2.22)

Учитывая, что dj/dt=e, a dh/dt = v, выражение (2.22) запишем в виде

где а г и аnсоответственно касательная и нормальная составляющие полного ускорения точки тела при вращательном движении, определяемые из выражений

Касательная составляющая полного ускорения точки тела (касательное ускорение) atхарактеризует изменение вектора скорости по модулю и направ­лена по касательной к траектории движения точки тела в направлении вектора скорости при ускоренном движении либо в противоположном направлении при замедленном движении. Модуль вектора касательного ускорения точки тела при вращательном движении твердого тела определяется выражением

(2,25)

Нормальная составляющая полного ускорения (нормальное ускорение) а„ возникает вследствие изменения направления вектора скорости точки при крашении твердого тела. Как следует из выражения (2.24) для нормального ускорения, это ускорение направлено по радиусу hк центру окружности, по которой перемещается точка. Модуль вектора нормального ускорения точки при вращательном движении твердого тела определяется с учетом (2.20) вы­ражением

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие – нибудь две точки, принадлежащие телу (или неизменно связанные с ним), остаются во все время движения неподвижными (рис. 2.2).

Рисунок 2.2

Проходящая через неподвижные точки А иВ прямая называетсяосью вращения. Так как расстояние между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси будут неподвижны, а все остальные будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направлена осьAz , полуплоскостьІ – неподвижную и полуплоскостьІІ врезанную в само тело и вращающуюся вместе с ним. Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком угломφ между этими плоскостями, который назовемуглом поворота тела. Будем считать уголφ положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца осиAz ), а отрицательным, если по ходу часовой стрелки. Измерять уголφ будем в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость углаφ от времениt , т.е.

.

Это уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ω и угловое ускорениеε.

9.2.1. Угловая скорость и угловое ускорение тела

Величина, характеризующая быстроту изменения угла поворота φ с течением времени, называется угловой скоростью.

Если за промежуток времени
тело совершает поворот на угол
, то численно средней угловой скоростью тела за этот промежуток времени будет
. В пределе при
получим

Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени.

Правило знаков: когда вращение происходит против хода часовой стрелки, ω> 0, а когда по ходу часовой стрелки, тоω< 0.

или, так как радиан – величина безразмерная,
.

В теоретических выкладках удобнее пользоваться вектором угловой скорости , модуль которого равени который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно против хода часовой стрелки. Этот вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.

Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.

Если за промежуток времени
приращение угловой скорости равно
, то отношение
, т.е. определяет значение среднего ускорения вращающегося тела за время
.

При стремлении
получаем величину углового ускорения в моментt :

Таким образом, числовое значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела во времени.

В качестве единицы измерения обычно применяют или, что тоже,
.

Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным , а если убывает, -замедленным. Когда величиныω иε имеют одинаковые знаки, то вращение будет ускоренным, когда разные – замедленным.По аналогии с угловой скоростью угловое ускорение также можно изобразить в виде вектора, направленного вдоль оси вращения. При этом

.

Если тело вращается ускоренно направление совпадает с, и противоположнопри замедленном вращении.

Если угловая скорость тела остается во время движения постоянной (ω= const ), то вращение тела называетсяравномерным .

Из
имеем
. Отсюда, считая, что в начальный момент времени
угол
, и беря интегралы слева отдо, а справа от 0 доt , получим окончательно

.

При равномерном вращении, когда =0,
и
.

Скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость междуn об/мин иω 1/с. При одном обороте тело повернется на 2π, а приn оборотах на 2π n ; этот поворот делается за 1 мин, т.е.t = 1мин=60с. Из этого следует, что

.

Если угловое ускорение тела во все время движения остается постоянным (ε= const ), то вращение называетсяравнопеременным .

В начальный момент времени t =0 угол
, а угловая скорость
(- начальная угловая скорость).
;
=ε
. Интегрируя левую часть отдо, а правую от 0 доt , найдем

Угловая скорость ω этого вращения
. Если ω и ε имеют одинаковые знаки, вращение будетравноускоренным , а если разные –равнозамедленным.

И Савельева .

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин , § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a t и a n .

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость - величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f" (t).

Угловое ускорение - величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f"" (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ об и φ об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие - скорость вращения тела (угловую скорость), но в различных единицах - в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a t и a n , характеризующими движение различных точек этого тела (рис 205).

Если R - расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ - углом поворота тела и s - расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности - совершает криволинейное движение.

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ 0 + ωt.

В частном случае, когда начальный угол поворота φ 0 =0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T - период вращения тела; φ=2π - угол поворота за один период.

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела - частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ 0 + ω 0 t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω 0 + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ 0 , ω 0 и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ 0 + (ω + ω 0)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ 0 + (ω 2 - ω 0 2)/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ 0 =0 и ω 0 =0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

Поступательным называется такое движение твердого тела, при котором любая прямая, неизменно связанная с этим телом, остается параллельной своему начальному положению.

Теорема. При поступательном движении твердого тела все его точки описывают одинаковые траектории и в каждый данный момент имеют равные по модулю и направлению скорости и ускорения.

Доказательство. Проведем через две точки и, поступательно движущегося тела отрезок
и рассмотрим движение этого отрезка в положении
. При этом точкаописывает траекторию
, а точка– траекторию
(рис. 56).

Учитывая, что отрезок
перемещается параллельно самому себе, и длина его не меняется, можно установить, что траектории точекибудут одинаковы. Значит, первая часть теоремы доказана. Будем определять положение точекивекторным способом относительно неподвижного начала координат. При этом эти радиусы – вектора находятся в зависимости
. Так как. ни длина, ни направление отрезка
не меняется при движении тела, то вектор

. Переходим к определению скоростей по зависимости (24):

, получаем
.

Переходим к определению ускорений по зависимости (26):

, получаем
.

Из доказанной теоремы следует, что поступательное движение тела будет вполне определено, если известно движение только одной какой- нибудь точки. Поэтому изучение поступательного движения твердого тела сводится к изучению движения одной его точки, т.е. к задаче кинематики точки.

Тема 11. Вращательное движение твердого тела

Вращательным называется такое движение твердого тела, при котором две его точки остаются неподвижными за все время движения. При этом прямая, проходящая через эти две неподвижные точки, называется осью вращения .

Каждая точка тела, не лежащая на оси вращения, описывает при таком движении окружность, плоскость которой перпендикулярна к оси вращения, и центр ее лежит на этой оси.

Проводим через ось вращения неподвижную плоскость I и подвижную плоскость II, неизменно связанную с телом и вращающуюся вместе с ним (рис. 57). Положение плоскости II, а соответственно и всего тела, по отношению к плоскости I в пространстве, вполне определятся углом . При вращении тела вокруг осиэтот угол является непрерывной и однозначной функцией времени. Следовательно, зная закон изменения этого угла с течением времени, мы сможем определить положение тела в пространстве:

- закон вращательного движения тела . (43)

При этом будем полагать, что угол отсчитывается от неподвижной плоскости в направлении обратном движению часовой стрелки, если смотреть с положительного конца оси. Так как положение тела, вращающегося вокруг неподвижной оси, определяется одним параметром, то говорят, что такое тело имеет одну степень свободы.

Угловая скорость

Изменение угла поворота тела с течением времени называется угловой скоростью тела и обозначается
(омега):

.(44)

Угловая скорость так же, как и линейная скорость, есть величина векторная, и этот вектор строят на оси вращения тела. Он направляется вдоль оси вращения в ту сторону, чтобы, смотря с его конца на его начало, видеть вращение тела против хода часовой стрелки (рис. 58). Модуль этого вектора определяется зависимостью (44). Точку приложенияна оси можно выбирать произвольно, так как вектор можно переносить вдоль линии его действия. Если обозначить орт-вектор оси вращения через, то получим векторное выражение угловой скорости:

. (45)

Угловое ускорение

Быстрота изменения угловой скорости тела с течением времени называется угловым ускорением тела и обозначается (эпсилон):

. (46)

Угловое ускорение есть величина векторная, и этот вектор строят на оси вращения тела. Он направляется вдоль оси вращения в ту сторону, чтобы, смотря с его конца на его начало, видеть направление вращение эпсилон против хода часовой стрелки (рис. 58). Модуль этого вектора определяется зависимостью (46). Точку приложенияна оси можно выбирать произвольно, так как вектор можно переносить вдоль линии его действия.

Если обозначить орт-вектор оси вращения через , то получим векторное выражение углового ускорения:

. (47)

Если угловые скорость и ускорения одного знака, то тело вращается ускоренно , а если разного – замедленно . Пример замедленного вращения показан на рис. 58.

Рассмотрим частные случаи вращательного движения.

1. Равномерное вращение:

,
.

,
,
,

,
. (48)

2. Равнопеременное вращение:

.

,
,
,
,
,
,
,
,

,
,
.(49)

Связь линейных и угловых параметров

Рассмотрим движение произвольной точки
вращающегося тела. При этом траектория движения точки будет окружность, радиуса
, расположенная в плоскости перпендикулярной оси вращения (рис. 59,а ).

Допустим, что в момент времени точка находится в положении
. Предположим, что тело вращается в положительном направлении, т.е. в направлении возрастания угла . В момент времени
точка займет положение
. Обозначим дугу
. Следовательно, за промежуток времени
точка прошла путь
. Ее средняя скорость , а при
,
. Но, из рис. 59,б , видно, что
. Тогда. Окончательно получаем

. (50)

Здесь - линейная скорость точки
. Как было получено ранее, эта скорость направлена по касательной к траектории в данной точке, т.е. по касательной к окружности.

Таким образом, модуль линейной (окружной) скорости точки вращающегося тела равен произведению абсолютного значения угловой скорости на расстояние от этой точки до оси вращения.

Теперь свяжем линейные составляющие ускорения точки с угловыми параметрами.

,
. (51)

Модуль касательного ускорения точки твердого тела, вращающегося вокруг неподвижной оси, равен произведению углового ускорения тела на расстояние от этой точки до оси вращения.

,
. (52)

Модуль нормального ускорения точки твердого тела, вращающегося вокруг неподвижной оси, равен произведению квадрата угловой скорости тела на расстояние от этой точки до оси вращения.

Тогда выражение для полного ускорения точки принимает вид

. (53)

Направления векторов ,,показаны на рисунке 59,в .

Плоским движением твердого тела называется такое движение, при котором все точки тела перемещаются параллельно некоторой неподвижной плоскости. Примеры такого движения:

Движение любого тела, основание которого скользит по данной неподвижной плоскости;

Качение колеса по прямолинейному участку пути (рельсу).

Получим уравнения плоского движения. Для этого рассмотрим плоскую фигуру, движущуюся в плоскости листа (рис. 60). Отнесем это движение к неподвижной системе координат
, а с самой фигурой свяжем подвижную систему координат
, которая перемещается вместе с ней.

Очевидно, что положение движущейся фигуры на неподвижной плоскости определяется положением подвижных осей
относительно неподвижных осей
. Такое положение определяется положением подвижного начала координат, т.е. координатами,и углом поворота, подвижной системы координат, относительно неподвижной, который будем отсчитывать от осив направлении обратном движению часовой стрелки.

Следовательно, движение плоской фигуры в ее плоскости будет вполне определено, если для каждого момента времени будут известны значения ,,, т.е. уравнения вида:

,
,
. (54)

Уравнения (54) являются уравнениями плоского движения твердого тела, так как если эти функции известны, то для каждого момента времени можно из этих уравнений найти соответственно ,,, т.е. определить положение движущейся фигуры в данный момент времени.

Рассмотрим частные случаи:

1.

, тогда движение тела будет поступательным, так как подвижные оси перемещаются, оставаясь параллельными своему начальному положению.

2.

,

. При таком движении меняется только угол поворота, т.е. тело будет вращаться относительно оси, проходящей перпендикулярно плоскости рисунка через точку.

Разложение движения плоской фигуры на поступательное и вращательное

Рассмотрим два последовательных положения и
, которые занимает тело в моменты времении
(рис. 61). Тело из положенияв положение
можно перенести следующим образом. Перенесем сначала телопоступательно . При этом отрезок
переместится параллельно самому себе в положение
, а затемповернем тело вокруг точки (полюса) на угол
до совпадения точеки.

Следовательно, любое плоское движение можно представить как сумму поступательного движения вместе с выбранным полюсом и вращательного движения , относительно данного полюса.

Рассмотрим методы, с помощью которых можно определить скорости точек тела, совершающего плоское движение.

1. Метод полюса. Этот метод основывается на полученном разложении плоского движения на поступательное и вращательное. Скорость любой точки плоской фигуры можно представить в виде двух составляющих: поступательной, со скоростью равной скорости произвольно выбранной точки – полюса , и вращательной вокруг этого полюса.

Рассмотрим плоское тело (рис. 62). Уравнения движения имеют вид:
,
,
.

Определяем из этих уравнений скорость точки (как при координатном способе задания)

,
,
.

Таким образом, скорость точки - величина известная. Принимаем эту точку за полюс и определим скорость произвольной точки
тела.

Скорость
будет складываться из поступательной составляющей, при движении вместе с точкой, и вращательной
, при вращении точки
относительно точки. Скорость точкиперенесем в точку
параллельно самой себе, так как при поступательном движении скорости всех точек равны как по величине, так и по направлению. Скорость
определится по зависимости (50)
, и направлен этот вектор перпендикулярно радиусу
по направлению вращения
. Вектор
будет направлен по диагонали параллелограмма, построенного на векторахи
, а его модуль определиться зависимостью:

, .(55)

2. Теорема о проекциях скоростей двух точек тела.

Проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой.

Рассмотрим две точки тела и(рис. 63). Принимая точкуза полюс, определим направлениепо зависимости (55):
. Проектируем это векторное равенство на линию
и, учитывая, что
перпендикулярно
, получаем

3. Мгновенный центр скоростей.

Мгновенным центром скоростей (МЦС) называется точка, скорость которой в данный момент времени равна нулю.

Покажем, что если тело движется не поступательно, то такая точка в каждый момент времени существует и притом единственная. Пусть в момент времени точкиитела, лежащие в сечении, имеют скоростии, не параллельные друг другу (рис. 64). Тогда точка
, лежащая на пересечении перпендикуляров к векторами, и будет МЦС, так как
.

Действительно, если допустить, что
, то по теореме (56), вектор
должен быть одновременно перпендикулярен
и
, что невозможно. Из этой же теоремы видно, что никакая другая точка сеченияв этот момент времени не может иметь скорость равную нулю.

Применяя метод полюса
- полюс, определим скорость точки(55):, т.к.
,
. (57)

Аналогичный результат можно получить для любой другой точки тела. Следовательно, скорость любой точки тела равна ее вращательной скорости относительно МЦС:

,
,
, т.е. скорости точек тела пропорциональны их расстояниям до МЦС.

Из рассмотренных трех способов определения скоростей точек плоской фигуры видно, что предпочтительным является МЦС, так как здесь скорость сразу определяется как по модулю, так и по направлению одной составляющей. Однако этот способ можно применять, если нам известен или мы можем определить для тела положение МЦС.

Определение положения МЦС

1. Если нам известны для данного положения тела направления скоростей двух точек тела, то МЦС будет точкой пересечения перпендикуляров к этим векторам скоростей.

2. Скорости двух точек тела антипараллельны (рис. 65,а ). В этом случае перпендикуляр к скоростям будет общим, т.е. МЦС находится где-то на этом перпендикуляре. Чтобы определить положение МЦС, надо соединить концы векторов скоростей. Точка пересечения этой линии с перпендикуляром будет искомым МЦС. При таком случае МЦС находится между этими двумя точками.

3. Скорости двух точек тела параллельны, но не равны по величине (рис.65,б ). Процедура получения МЦС аналогична описанной в пункте 2.

г) Скорости двух точек равны как по величине, так и по направлению (рис.65,в ). Получаем случай мгновенно поступательного движения, при котором скорости всех точек тела равны. Следовательно, угловая скорость тела в данном положении равна нулю:

4. Определим МЦС для колеса, катящегося без скольжения по неподвижной поверхности (рис. 65,г ). Так как движение происходит без скольжения, то в точке контакта колеса с поверхностью скорость будет одинакова и равна нулю, так как поверхность неподвижна. Следовательно, точка контакта колеса с неподвижной поверхностью будет являться МЦС.

Определение ускорений точек плоской фигуры

При определении ускорений точек плоской фигуры прослеживается аналогия с методами определения скоростей.

1. Метод полюса. Так же, как и при определении скоростей, принимаем за полюс произвольную точку тела, ускорение которой нам известно, или мы можем его определить. Тогда ускорение любой точки плоской фигуры равно сумме ускорений полюса и ускорения во вращательном движении вокруг этого полюса:

При этом составляющая
определяет ускорение точкипри ее вращении вокруг полюса. При вращении траектория движения точки будет криволинейной, а значит
(рис. 66).

Тогда зависимость (58) принимает вид
. (59)

Учитывая зависимости (51) и (52), получаем
,
.

2. Мгновенный центр ускорений.

Мгновенным центром ускорений (МЦУ) называется точка, ускорение которой в данный момент времени равно нулю.

Покажем, что в каждый данный момент времени такая точка существует. Принимаем за полюс точку , ускорение которой
нам известно. Находим угол, лежащий в пределах
, и удовлетворяющий условию
. Если
, то
и наоборот, т.е. уголоткладывается по направлению. Отложим от точкипод угломк вектору
отрезок
(рис. 67). Полученная такими построениями точка
будет МЦУ.

Действительно, ускорение точки
равно сумме ускорений
полюсаи ускорения
во вращательном движении вокруг полюса:
.

,
. Тогда
. С другой стороны, ускорение
образует с направлением отрезка
угол
, который удовлетворяет условию
. Знак минус поставлен перед тангенсом угла, так как вращение
относительно полюсапротив хода часовой стрелки, а угол
откладывается по ходу часовой стрелке. Тогда
.

Следовательно,
и тогда
.

Частные случаи определения МЦУ

1.
. Тогда
, и, следовательно, МЦУ не существует. В этом случае тело движется поступательно, т.е. скорости и ускорения всех точек тела равны.

2.
. Тогда
,
. Значит, МЦУ лежит на пересечении линий действия ускорений точек тела (рис.68,а ).

3.
. Тогда,
,
. Значит, МЦУ лежит на пересечении перпендикуляров к ускорениям точек тела (рис.68,б ).

4.
. Тогда
,

. Значит, МЦУ лежит на пересечении лучей, проведенных к ускорениям точек тела под углом(рис.68,в ).

Из рассмотренных частных случаев можно сделать вывод: если принять точку
за полюс, то ускорение любой точки плоской фигуры определится ускорением во вращательном движении вокруг МЦУ:

. (60)

Сложным движением точки называется такое движение, при котором точка одновременно участвует в двух или более движениях. При таком движении положение точки определяют относительно подвижной и относительно неподвижной систем отсчета.

Движение точки относительно подвижной системы отсчета называется относительным движением точки . Параметры относительного движения условимся обозначать
.

Движение той точки подвижной системы отсчета, с которой в данный момент совпадает движущаяся точка относительно неподвижной системы отсчета, называется переносным движением точки . Параметры переносного движения условимся обозначать
.

Движение точки относительно неподвижной системы отсчета называется абсолютным (сложным) движением точки . Параметры абсолютного движения условимся обозначать
.

В качестве примера сложного движения, можно рассмотреть движение человека в движущемся транспорте (трамвай). В этом случае движение человека отнесено к подвижной системе координат – трамваю и к неподвижной системе координат – земле (дороге). Тогда исходя из данных выше определений, движение человека относительно трамвая – относительно, движение вместе с трамваем относительно земли – переносное, а движение человека относительно земли – абсолютное.

Будем определять положение точки
радиусами – векторами относительно подвижной
и неподвижной
систем координат (рис. 69). Введем обозначения:- радиус-вектор, определяющий положение точки
относительно подвижной системы координат
,
;- радиус-вектор, определяющий положение начала подвижной системы координат (точки) (точки);- радиус – вектор, определяющий положение точки
относительно неподвижной системы координат
;
,.

Получим условия (ограничения), соответствующие относительному, переносному и абсолютному движениям.

1. При рассмотрении относительного движения будем считать, что точка
перемещается относительно подвижной системы координат
, а сама подвижная система координат
относительно неподвижной системы координат
не перемещается.

Тогда координаты точки
будут меняться в относительном движении, а орт-вектора подвижной системы координат изменяться по направлению не будут:

,

,

.

2. При рассмотрении переносного движения, будем считать, что координаты точки
по отношению к подвижной системе координат зафиксированы, и точка перемещается вместе с подвижной системой координат
относительно неподвижной
:

,

,

,.

3. При абсолютном движении точка движется и относительно
и вместе с системой координат
относительно неподвижной
:

Тогда выражения для скоростей, с учетом (27), имеют вид

,
,

Сравнивая эти зависимости, получаем выражение для абсолютной скорости:
. (61)

Получили теорему о сложении скоростей точки в сложном движении: абсолютная скорость точки равна геометрической сумме относительной и переносной составляющих скорости.

Используя зависимость (31), получаем выражения для ускорений:

,

Сравнивая эти зависимости, получаем выражение для абсолютного ускорения:
.

Получили, что абсолютное ускорение точки не равно геометрической сумме относительной и переносной составляющих ускорений. Определим составляющую абсолютного ускорения, стоящую в скобках, для частных случаев.

1. Переносное движение точки поступательное
. В этом случае оси подвижной системы координат
перемещаются все время параллельно самим себе, тогда.

,

,

,
,
,
, тогда
. Окончательно получаем

. (62)

Если переносное движение точки поступательное, то абсолютное ускорение точки равно геометрической сумме относительной и переносной составляющей ускорения.

2. Переносное движение точки непоступательное. Значит, в этом случае подвижная система координат
вращается вокруг мгновенной оси вращения с угловой скоростью(рис. 70). Обозначим точку на конце векторачерез. Тогда, используя векторный способ задания (15), получаем вектор скорости этой точки
.

С другой стороны,
. Приравнивая правые части этих векторных равенств, получаем:
. Поступая аналогично, для остальных орт векторов, получаем:
,
.

В общем случае абсолютное ускорение точки равно геометрической сумме относительной и переносной составляющей ускорения плюс удвоенное векторное произведение вектора угловой скорости переносного движения на вектор линейной скорости относительного движения.

Удвоенное векторное произведение вектора угловой скорости переносного движения на вектор линейной скорости относительного движения называется ускорением Кориолиса и обозначается

. (64)

Ускорение Кориолиса характеризует изменение относительной скорости в переносном движении и изменение переносной скорости в относительном движении.

Направляется
по правилу векторного произведения. Вектор ускорения Кориолиса всегда направлен перпендикулярно плоскости, которую образуют вектораи, таким образом, чтобы, смотря с конца вектора
, видеть поворотк, через наименьший угол, против хода часовой стрелки.

Модуль ускорения Кориолиса равен.

Вращением твердого тела вокруг неподвижной оси (оси вращения) называется такое его движение, при котором точки тела, лежащие на оси вращения, остаются неподвижными в течение всего времени движения.

Пусть осью вращения является ось , которая может иметь в пространстве любое направление. Одно направление оси принимается за положительное (рис. 28).

Через ось вращения проведем неподвижную плоскость и подвижную , скрепленную с вращающимся телом. Пусть в начальный момент времени обе плоскости совпадают. Тогда в момент времени положение подвижной плоскости и самого вращающегося тела можно определить двугранным углом между плоскостями и соответствующим линейным углом между прямыми, расположенными в этих плоскостях и перпендикулярными оси вращения. Угол называется углом поворота тела .

Положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени, если задано уравнение

где – любая, дважды дифференцируемая функция времени. Это уравнение называют уравнением вращения твердого тела вокруг неподвижной оси .

У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла .

Угол считается положительным, если он откладывается против часовой стрелки, и отрицательным – в противоположном направлении, если смотреть с положительного направления оси . Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных оси вращения.

Для характеристики вращательного движения твердого тела вокруг неподвижной оси введем понятия угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени называют первую производную по времени от угла поворота в этот момент, т.е. . Она является величиной положительной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.

Модуль угловой скорости обозначают . Тогда

Алгебраическим угловым ускорением тела называют первую производную по времени от алгебраической скорости, т.е. вторую производную от угла поворота . Модуль углового ускорения обозначим , тогда

Если при , то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону (против часовой стрелки). При и , тело вращается ускоренно в отрицательную сторону. Если при , то имеем замедленное вращение в положительную сторону. При и замедленное вращение совершается в отрицательную сторону.