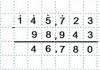
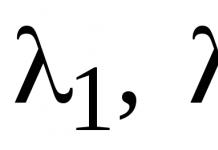Уравнение ван дер ваальса онлайн. Уравнение Ван-дер-Ваальса

Уравнение Ван–дер–Ваальса:

где постоянные поправки а и b зависят от природы газа.

Поправка b учитывает объем, недоступный для движения молекул в силу конечности объема самих молекул и наличия взаимодействия между ними. Величина b составляет примерно учетверенный объем самих молекул.

Поправка а учитывает силы взаимного притяжения. Полагая, что внутреннее давление газа изменяется пропорционально квадрату плотности или обратно пропорционально квадрату удельного объема газа, Ван-дер-Ваальс принял его равным а/J 2 , где а – коэффициент пропорциональности.

Раскрывая скобки в левой части:

Умножая равенство на J 2 и разделив на р :

Полученное уравнение имеет три корня, т.е. при заданных параметрах р и Т имеется три значения переменной J, которые превращают уравнение в тождество.

Рассмотрим в системе координат р–J изотермы, построенные по уравнению Ван-дер-Ваальса.

Первый случай имеет место при высоких температурах, когда изотермы имеют вид кривых гиперболического характера (линия 1-2). Каждому давлению соответствует определенный удельный объем (давлению р а соответствует удельный объем J а). Тело в этом случае при любых давлениях находится в газообразном состоянии.

Второй случай имеет место при сравнительно низких температурах, когда изотермы имеют два перегиба (линия 3-4).

В этом случае между точками e и f находится область, в которой каждому давлению соответствует три значения удельного объема (давлению р а соответствуют удельные объемы J b , J с и J d), которые и являются тремя действительными и различными корнями уравнения Ван-дер-Ваальса.

Участок 3-b соответствует изотермическому сжатию тела, находящегося в газообразном состоянии, причем в точке b оно уже начинает переходить в жидкое состояние.

Точка d соответствует такому состоянию тела, когда оно уже полностью превратилось в жидкость, в соответствии с чем участок d-4 представляет собой изотермическое сжатие жидкости.

Точка с соответствует промежуточному двухфазному состоянию тела. Участок кривой b-f соответствует неустойчивому состоянию пара, а участок d-e – неустойчивому состоянию жидкости.

Что касается участка e-f, то он вообще физического смысла не имеет, поскольку в действительности при изотермическом сжатии тело переходит из газообразного в жидкое состояния при постоянном давлении, т.е. по горизонтальной линии b-d.

Третий случай имеет место при определенной для каждого тела температуре, когда точки b и d, сближаясь с повышением температуры, сливаются в одну точку k, в которой имеет место перегиб соответствующей изотермы, причем касательная к ней в этой точке имеет горизонтальное направление.

Точка k называется критической точкой, выше которой невозможно путем изотермического сжатия добиться перехода газа в жидкое состояние, а соответствующие ей параметры р кр, J кр и Т кр называются критическими параметрами.

Аналитически условия критического состояния тела выражаются уравнениями

Первое из них показывает, что критическая изотерма в точке k имеет горизонтальную касательную, второе – что изотерма имеет в точке k перегиб.

Используя эти уравнения совместно с уравнением состояния, можно определить значения критических параметров состояния газа.

Критические параметры определяются следующим образом .

Преобразуем уравнение Ван-дер-Ваальса:

Дифференцируем:

Определяем вторую производную:

Разделив первое уравнение на второе

и, следовательно ,

откуда

Уравнение Ван-дер-Ваальса можно представить в безразмерном виде с подстановкой.

Наиболее известным уравнением состояния реальных газов, учитывающим собственный объем молекул газа и их взаимодействие, является уравнение (1873г.) нидерландского физика И.Д. Ван-дер-Ваальса (1837–1923). Рассмотрим коротко вывод этого уравнение.

Конечный объем (размеры) молекул увеличивает давление реального газа по сравнению с ИГ, т.к. передача импульса стенкам через пространство сосуда осуществляется быстрее, чем точечными молекулами вследствие прохождения ими между столкновениями меньшего пути. Учитывают только (силы отталкивания) парные столкновения молекул – столкновение двух молекул, когда остальные на них не действуют. Вероятностью и влиянием одновременных тройных, четверных и т.д. столкновений пренебрегают. При расчете давления можно считать, что одна молекула остается неподвижной, а другая движется с удвоенной кинетической энергией. При столкновении центры молекул могут сблизиться на расстояние, меньшее d – диаметр молекулы, поэтому можно считать неподвижную молекулу окруженной сферой ограждения радиуса d , а движущуюся молекулу точечной. Если применить такое приближение к газу из N молекул, то половина молекул N/2 будет покоится (окружена сферами ограждения), а другая половина может рассматриваться как газ из N 1 =N/ 2с температурой T 1 =2T . Этому газу был бы доступен объем сосуда V за исключением объема b всех сфер ограждения N/ 2 покоящихся молекул, т.е. V–b . Тогда согласно уравнению (9.12), давление, оказываемое этими молекулами на стенку сосуда, имеет вид

или для одного моля газа .

Очевидно, что объем b приблизительно равен учетверенному объему всех молекул газа (рис. 13.2). Учтем теперь действие сил притяжения между молекулами газа. Когда молекула находится внутри вещества (газа), то силы притяжения со стороны остальных молекул со всех сторон примерно скомпенсированы. Если же молекула находится в поверхностном слое, то появляется некомпенсированная сила притяжения F , направленная от поверхности внутрь газа. Под действием этих сил молекула может вообще не долететь до стенки сосуда, а отразиться от поверхностного слоя вещества. Действие сил притяжения создает добавочное – внутреннее или молекулярное давление P i ~N сл F , где N сл – число молекул в приповерхностном (пристеночном) слое. Величины N сл и F прямо пропорциональны плотности и обратно пропорциональны объему газа. Для одного моля газа P i =а/V m 2 и реальное давление газа равно , где Р – давление ИГ. Для неплотных газов поправки на силы отталкивания и притяжения можно вводить независимо, тогда обобщая, получим

(13.2)

или для произвольного количества вещества с учетом V =nV m :

. (13.3)

Уравнение (13.3)– уравнение Ван-дер-Ваальса , a и b – константы, поправки Ван-дер-Ваальса.

Уравнение (13.2), рассматриваемое как уравнение для определения объема при данных Т и Р , есть уравнение третьей степени, в преобразованном виде оно имеет вид

. (13.4)

Так как уравнение третьей степени с вещественными коэффициентами может иметь либо один вещественный корень и два комплексно сопряженных, либо три вещественных корня, то на плоскости PV прямая, параллельная оси V , может пересекать изотерму либо в трех точках, либо в одной. Построение по точкам изотермы Ван-дер-Ваальса приводит к семейству кривых, изображенных на рис. 13.3 (теоретически Ван-дер-Ваальс, экспериментально Т. Эндрюс (1813–1885) для СО 2 ).

Левая, круто спадающая ветвь соответствует малому изменению объема при изменении давления, что характерно для жидкого состояния вещества. Правая пологая ветвь соответствует значительному изменению объема при изменении давления, что соответствует газообразному состоянию вещества.

Переход из жидкого в газообразное состояние и обратно происходит не вдоль изотермы Ван-дер-Ваальса, а вдоль изобары АЕ , которая одновременно является и изотермой реального газа. При этом площади фигур АВС и СDЕ равны (правило Максвелла ). Точки изотермы А и Е изображают двухфазные состояния вещества, а между ними существуют одновременно две фазы. Чем ближе изображающая точка G к А , тем больше в системе жидкости, чем ближе к Е – тем больше пара. Если обозначить максимальный объем моля жидкости и минимальный объем пара в системе при температуре Т через V 1 и V 2 соответственно, а объем двухфазной области в точке G через V 0 , то , где х – мольная доля жидкости в состоянии G ; отсюда, зная объем V 0 , можно найти и долю x жидкости. Участки АВ и DЕ изотермы Ван-дер-Ваальса изображают метастабильные состояния вещества: переохлажденную жидкость и пересыщенный пар , которые могут существовать при известных условиях (при очень медленном квазиравновесном проведении процесса и тщательной подготовки, например, удалении всех загрязнений из объема нагреваемой жидкости и со стенок сосуда, т.к. процесс кипения начинается легче на посторонних частицах – включениях). Участок ВD соответствует абсолютно неустойчивым (рост давления при росте объема) состояниям вещества и ни при каких условиях не реализуется. При достаточно низких температурах участок АВС может опускаться ниже оси OV , что адекватно отрицательному давлению, соответствующему состоянию растянутой жидкости (за счет действия сил поверхностного натяжения).

С ростом температур область горбов и впадин на изотерме Ван-дер-Ваальса уменьшается и при температуре Т к – критической температуре – превращается в точку перегиба с горизонтальной касательной. Для этой точки уравнение (13.4) имеет три одинаковых корня и принимает вид . Критические параметры данного газа определяют по формулам

газ плазма кинетика термодинамический

В газе взаимодействие между молекулами слабо. По мере его усиления свойства газа все ближе отклоняются от свойств идеальных газов, и, в конце концов, переходит в концентрированное состояние - жидкость. В жидкости взаимодействие между молекулами велико и, следовательно, свойства жидкости зависят от конкретного рода жидкости. Поэтому невозможно установить какие либо общие формулы, которые количественно описывали бы свойства жидкости. Можно, однако, найти некоторую интерполяционную формулу, качественно описывающую переход между жидкостью и газом. Эта формула должна давать правильные результаты в двух предельных случаях. Для разреженных газов она должна переходить в формулы идеальных газов. При увеличении плотности она должна учитывает ограниченную сжимаемость веществ. Для получения такой формулы исследуем более подробно исследовать отклонение от идеальности при высоких температурах. Будем рассматривать одноатомный газ. По тем же соображениям формулы будут применимы и к многоатомным газам. Описанный ранее характер взаимодействия атомов газа позволяет определить вид первых членов разложения В(Т) относительно степени, обратной Т, при этом будем считать малым отношение U 0 /kT << 1.

Имея в виду, что U 12 есть функция только расстояния r между атомами, имеем. Разбивая область интегрирования по dr на две части, запишем:

Но при значениях r от 0 до 2r 0 потенциальная энергия U 12 очень велика. Поэтому в первом интеграле можно пренебречь членом exp(-U 12 /kT) по сравнению с единицей. Тогда интеграл становится равным положительной величине b = 16рr 0 3 /3 (если для одноатомного газа рассматривать r как радиус атома, то b есть его учетверенный объем). Во втором интеграле везде |U 12 |/kT < U 0 /kT << 1. Поэтому можно разложить подынтегральное выражение по степеням U 12 /kT, ограничиваясь первым неисчезающим членом. Тогда второй интеграл становится равным

где а - положительная постоянная. Таким образом, находим, что

Находим свободную энергию газа

Подставим в это выражение

которое мы получали раньше из статистической суммы для идеального газа. Тогда получим

При выводе формулы для свободной энергии газа мы предполагаем, что газ, недостаточного разрежен для того, чтобы считаться идеальным, однако имеет достаточно большой объем (так, что было можно пренебречь тройными и т.д. взаимодействиями), т.е. расстояние между молекулами значительно больше, чем их размеры. Можно сказать, что объем V газа, во всяком случае, значительно больше, чем Nb. Поэтому

Следовательно

В таком виде эта формула удовлетворяет поставленным выше условиям, т.к. при больших V она переходит в формулу для свободной энергии идеального газа, а при малых V она обнаруживает невозможность беспредельного сжатия газа (при V < Nb аргумент логарифма становится отрицательным). Зная свободную энергию, можно определить давление газа:

Это и есть искомое уравнения состояния реального газа - уравнение Ван-дер-Ваальса. Она является лишь одной из многих возможных интерполяционных формул. Ян Ван-дер-Ваальс вывел это уравнение в 1873 году (нобелевская премия 1910 года).

Энтропия реального газа из (*):

Энергия E = F + TS

Отсюда видно, что теплоемкость Ван-дер-Ваальсовского газа совпадет с теплоемкостью идеального газа (зависит только от Т) и может быть постоянной. Теплоемкость С р, как легко убедиться, зависит не только от Т, но и от V и поэтому не может сводиться к постоянной. Второй член в Е соответствует энергии взаимодействий газа. Он отрицателен, т.к. преобладают силы притяжения.

Приведенное уравнение состояния.

Запишем уравнение Ван-дер-Ваальса для одного моля газа:

Зависимости P(V) при постоянной температуре называются изотермами Ван-дер-Ваальса. Среди различных изотерм есть одна, которой соответствует критическое состояние, математически характеризуемое точкой перегиба. Приравнивая к нулю первую и вторую производные.

Для реальных газов пользоваться результатами теории идеального газа следует с большой осторожностью. Во многих случаях необходимо переходить к более реалистичным моделям. Одной из большого числа таких моделей может служить газ Ван-дер-Ваальса . В этой модели учитываются собственный объем молекул и взаимодействия между ними. В отличие от уравнения Менделеева - Клапейрона pV= RT, справедливого для идеального газа, уравнение газа Ван-дер-Ваальса содержит два новых параметра а и Ь, не входящих в уравнение для идеального газа и учитывающих межмолекулярные взаимодействия (параметр а) и реальный (отличный от нуля) собственный объем (параметр Ь) молекул. Предполагается, что учет взаимодействия между молекулами в уравнении состояния идеального газа сказывается на величине давления р, а учет их объема приведет к уменьшению свободного для движения молекул пространства - объема V, занимаемого газом. Согласно Ван-дер-Ваальсу уравнение состояния одного моль такого газа записывается в виде:

где Ум - молярный объем величины (а/Ум) и Ь описывают отклонения газа от идеальности.

Величина a/V^, по размерности соответствующая давлению, описывает взаимодействие молекул между собой на больших (по сравнению с размерами самих молекул) расстояниях и представляет так называемое добавочное к внешнему «внутреннее давление» газа р. Константа Ъ в выражении (4.162) учитывает суммарный объем всех молекул газа (равна учетверенному объему всех молекул газа).

Рис. 4.24. К определению константы b в уравнении Ван-дер-Ваальса

Действительно, на примере двух молекул (рис. 4.24) можно убедиться, что молекулы (как абсолютно жесткие шары) не могут сблизиться друг с другом на расстояние, меньшее, чем 2г между их центрами,

т.е. область пространства, «выключенная» из общего объема, занимаемого газом в сосуде, которая приходится на две молекулы, имеет объем

В пересчете на одну молекулу это

ее учетверенный объем.

Поэтому (V M - b) есть доступный для движения молекул объем сосуда. Для произвольного объема V и массы т газа с молярной массой М уравнение (4.162) имеет вид

Рис. 4.25.

где v = т/М - число моль газа, а а"= v 2 a и Ь"= vb - константы (поправки) Ван-дер-Ваальса.

Выражение для внутреннего давления газа в (4.162) записано в виде a/Vj, по следующей причине. Как было сказано в подразделе 1.4.4, потенциальная энергия взаимодействия между молекулами в первом приближении хорошо описывается потенциалом Леннард- Джонса (см. рис. 1.32). На сравнительно больших расстояниях этот потенциал может быть представлен в виде зависимости U ~ г~ ь, где г - расстояние между молекулами. Поскольку сила F взаимодействия между молекулами связана с потенциальной энергией U как F - -grad U(r), то F ~ -г 7 . Число молекул в объеме сферы радиуса г пропорционально г 3 , поэтому суммарная сила взаимодействия между молекулами пропорциональна it 4 , а дополнительное «давление» (сила, отнесенная к площади, пропорциональной г 2) пропорционально г ь (или ~ 1/F 2). При малых значениях г проявляется сильное отталкивание между молекулами, которое косвенно учитывается

коэффициентом Ь.

Уравнение Ван-дер-Ваальса (4.162) может быть переписано в виде полиномиального (вириального) разложения по степеням У м (или У):

Относительно V M это уравнение кубическое, поэтому при заданной температуре Т должно иметь либо один вещественный корень, либо три (далее, полагая, что мы по-прежнему имеем дело с одним моль газа, опустим индекс М в V M , чтобы не загромождать формулы).

На рисунке 4.25 в координатахp(V) при различных температурах Т приведены изотермы, которые получаются в качестве решений уравнения (4.163).

Как показывает анализ этого уравнения, существует такое значение параметра Т- Г* (критическая температура), которое качественно разделяет различные типы его решений. При Т > Т к кривые p(V) монотонно спадают с ростом V, что соответствует наличию одного действительного решения (одно пересечение прямой р = const с изотермой p(V)) - каждому значению давления р соответствует только одно значение объема V. Иными словами, при Т > Т к газ ведет себя примерно как идеальный (точного соответствия нет и оно получается только при Т -> оо, когда энергией взаимодействия между молекулами по сравнению с их кинетической энергией можно пренебречь). При низких температурах, когда Т одному значению р соответствует три значения V, и форма изотерм принципиально изменяется. При Г= Т к изотерма Ван-дер-Ваальса имеет одну особую точку (одно решение). Этой точке соответствуют /^(критическое давление) и V K (критический объем). Эта точка соответствует состоянию вещества, названному критическим, и, как показывают эксперименты, в этом состоянии вещество не является ни газом, ни жидкостью (промежуточное состояние).

Экспериментальное получение реальных изотерм может быть осуществлено с помощью простого устройства, схема которого изображена на рис. 4.26. Устройство - это цилиндр с подвижным поршнем и манометром для измерения давления р. Измерение объема V производят по положению поршня. Вещество в цилиндре поддерживается при определенной температуре Т (находится в термостате).

Рис. 4.26.

Меняя его объем (опуская или поднимая поршень) и измеряя при этом давление, получают изотермуp(V).

Оказывается, что полученные таким образом изотермы (сплошные линии на рис. 4.25) заметно отличаются от теоретических (штрихпунктирная линия). При Т = Т и большйх V уменьшение объема приводит к увеличению давления соответственно расчетной кривой до точки N (штрихпунктирная изотерма на рис. 4.25). После этого уменьшение V не приводит к дальнейшему росту р. Иными словами, точка N соответствует началу конденсации, т.е. переходу вещества из состояния пара в состояние жидкости. При уменьшении объема от точки N к точке М давление остается постоянным, меняется только соотношение между количествами жидкого и газообразного вещества в цилиндре. Давление соответствует равновесию между паром и жидкостью и называется давлением насыщенного пара (отмечено на рис. 4.25 как р„. п). В точке М все вещество в цилиндре представляет собой жидкость. При дальнейшем уменьшении объема изотермы резко поднимаются вверх, что соответствует резкому уменьшению сжимаемости жидкости по сравнению с паром.

При увеличении температуры в системе, т.е. при переходе от одной изотермы к другой, длина отрезка MN уменьшается (А/УУ"при Т 2 > Т), и при Т=Т К он стягивается в точку. Огибающая всех отрезков вида MN образует колоколообразную кривую (бинодаль) - пунктирная кривая MKN на рис. 4.25, отделяющую двухфазную область (под колоколом бинодали) от однофазной - пара или жидкости. При Т> Т к никаким увеличением давления газообразное вещество превратить в жидкость уже нельзя. Этим критерием можно воспользоваться для проведения условного различия между газом и паром: при Т вещество может существовать и в виде пара, и в виде жидкости, но при Т > Т к никаким давлением газ в жидкость перевести нельзя.

В тщательно поставленных экспериментах можно наблюдать так называемые метастабильные состояния, характеризуемые участками МО и NL на изотерме Ван-дер-Ваальса при Т= Т (штрихпунктирная кривая на рис. 4.25). Эти состояния отвечают переохлажденному пару (участок МО) и перегретой жидкости (участок NL). Переохлажденный пар - это такое состояние вещества, когда по своим параметрам оно должно находиться в жидком состоянии, но по своим свойствам продолжает следовать газообразному поведению - стремится, например, расшириться при увеличении объема. И наоборот, перегретая жидкость - такое состояние вещества, когда оно по своим параметрам должно быть паром, но по свойствам остается жидкостью. Оба эти состояния метастабильны (т.е. неустойчивы): при небольшом внешнем воздействии вещество переходят в стабильное однофазное состояние. Участок OL (определенный математически из уравнения Ван-дер- Ваальса) соответствует отрицательному коэффициенту сжатия (с увеличением объема растет и давление!), оно не реализуется в опытах ни при каких условиях.

Константы а и b считаются независящими от температуры и являются, вообще говоря, разными для разных газов. Можно, однако, модифицировать уравнение Ван-дер-Ваальса так, чтобы ему удовлетворяли любые газы, если их состояния описываются уравнением (4.162). Для этого найдем связь между константами а и b и критическими параметрами: р к, V K n Т к. Из (4.162) для моль реального газа получаем 1:

Воспользуемся теперь свойствами критической точки. В этой точке величины йр/dV и tfp/dV 2 равны нулю, так эта точка является точкой перегиба. Из этого следует система трех уравнений:

1 Индекс М при объеме моль газа опущен для упрощения записи. Здесь и далее константы а и Ь по-прежнему приведены к одному моль газа.

Эти уравнения справедливы для критической точки. Решение их относительно/>*, У к, Гадает:

и, соответственно,

Из последнего соотношения в этой группе формул, в частности, следует, что для реальных газов постоянная R оказывается индивидуальной (для каждого газа со своим набором рк, У к, Т к она своя), и только для идеального или для реального газа вдали от критической температуры (при Т » Т к) ее можно полагать равной универсальной газовой постоянной R = k b N A . Физический смысл указанного различия кроется в процессах кластерообразования, происходящих в реальных газовых системах в докритических состояниях.

Критические параметры и константы Ван-дер-Ваальса для некоторых газов представлены в табл. 4.3.

Таблица 4.3

Критические параметры и константы Ван-дер-Ваальса

Если теперь подставить эти значения из (4.168) и (4.169) в уравнение (4.162) и выразить давление, объем и температуру в так называемых приведенных (безразмерных) параметрах л = р/р к, со = V/V K , т = Т/Т к, то оно (4.162) перепишется как:

Это уравнение Ван-дер-Ваальса в приведенных параметрах универсальное для всех ван-дер-ваальсовых газов (т.е. реальных газов, подчиняющихся уравнению (4.162)).

Уравнение (4.170) позволяет сформулировать закон, связывающий три приведенные параметра - закон соответственных состояний: если у каких-либо различных газов совпадают два из трех (л, со, т) приведенных параметров, то должны совпадать и значения третьего параметра. Говорят, что такие газы находятся в соответственных состояниях.

Запись уравнения Ван-дер-Ваальса в виде (4.170) позволяет также распространить связанные с ним представления на случай произвольных газов, которые уже ван-дер-ваальсовскими не являются. Уравнение (4.162), записанное в виде (4.164): p(V) = RT/(V-b)-a/V 2 , напоминает по форме разложение функции р(У) в ряд по степеням V (до второго члена включительно). Если считать (4.164) первым приближением, то уравнение состояния любого газа можно представить в универсальном виде:

где коэффициенты А„(Т) называются вириальными коэффициентами.

При бесконечном числе членов этого разложения оно может точно описать состояние любого газа. Коэффициенты А„(Т) являются функциями температуры. В различных процессах используются различные модели, и для их расчета теоретически оценивается, каким количеством членов этого разложения необходимо пользоваться в случаях разного рода газов для получения желаемой точности результата. Конечно, все модели реальных газов зависят от выбранного вида межмолекулярного взаимодействия, принятого при рассмотрении конкретной задачи.

Предложена в 1873 г. голландским физиком Я.Д. Ван-дер-Ваальсом.

Уравнение Менделеева - Клапейрона является уравнением состояния идеального газа и довольно точно описывает поведение реальных газов при небольшой плотности, т.е. достаточно низком давлении и высокой температуре ( ).

При понижении температуры и увеличении давления, плотность газа увеличивается, а расстояние между его молекулами уменьшается, поэтому пренебрегать их объёмом и взаимо-

Рис. 23 действием мы не можем.

Силы взаимного притяжения между молекулами направлены внутрь газа, т. е. в сторону наибольшего окружения периферийных молекул (рис.23).

Действие этих сил подобно наличию некоторого добавочного давления на газ, называемого внутренним.

В связи с тем, что молекулы газа занимают конечные размеры, они занимают суммарный объём V / . Поэтому объём, предоставленный для передвижений молекулам, будет меньше на величину V" . Таким образом, для описания состояния реальных газов необходимо сделать две поправки:

а ) на дополнительное давление, обусловленное взаимодействием молекул;

б ) на уменьшение объёма, в связи с учётом размеров самих молекул.

Возьмём за основу уравнение состояния идеального газа и, внеся в него соответствующие поправки, получим уравнение состояния реального газа. Для одного моля газа имеем

Внесённые поправки были впервые рассчитаны и предложены Ван-дер-Ваальсом (гол.)

где а и в – постоянные Ван-дер-Ваальса.

Уравнение Ван-дер-Ваальса для одного моля реального газа имеет вид:

. (26)

Учитывая, что и, умножив обе части уравнения на , получим уравнение Ван-дер-Ваальса для любой массы газа: . (27)

Полученные нами уравнения имеют третью степень относительно V , например, для одного моля после преобразования, оно будет иметь вид:

Это означает, что оно может иметь либо три действительных, либо один действительный и два мнимых корня, при чём физический смысл имеют только действительные корни.

Эти особенности уравнения состояния нашли своё отражение в графиках зависимости p (V m ), называемых кривыми Ван-дер-Ваальса (рис. 24).