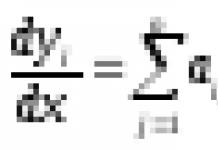Дифференциальное уравнение движения материальной точки под действием силы F можно представить в следующей векторной форме:

Так как масса точки m принята постоянной, то её можно внести под знак производной. Тогда

Формула (1) выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе .

В проекциях на координатные оси (1) можно представить в виде

Если обе части (1) умножить на dt , то получим другую форму этой же теоремы – теорему импульсов в дифференциальной форме:

т.е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.

Проецируя обе части (2) на координатные оси, получаем

Интегрируя обе части (2) в пределах от нуля до t (рис. 1), имеем

где - скорость точки в момент t ; - скорость при t = 0;

S - импульс силы за время t .

Выражение в форме (3) часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени.

В проекциях на координатные оси эту теорему можно представить в следующем виде:

Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.

Теорема об изменении количества движения системы

Количеством движения системы будем называть векторную величину Q , равную геометрической сумме (главному вектору) количеств движения всех точек системы.

Рассмотрим систему, состоящую изn материальных точек. Составим для этой системы дифференциальные уравнения движения и сложим их почленно. Тогда получим:

Последняя сумма по свойству внутренних сил равна нулю. Кроме того,

Окончательно находим:

Уравнение (4) выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил.

Найдём другое выражение теоремы. Пусть в момент t = 0 количество движения системы равно Q 0 , а в момент времени t 1 становится равным Q 1 . Тогда, умножая обе части равенства (4) на dt и интегрируя, получим:

Или , где:

(S- импульс силы)

так как интегралы, стоящие справа, дают импульсы внешних сил,

уравнение (5) выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.

В проекциях на оси координат будем иметь:

Закон сохранения количества движения

Из теоремы об изменении количества движения системы можно получить следующие важные следствия:

1. Пусть сумма всех внешних сил, действующих на систему, равна нулю:

Тогда из уравнения (4) следует, что при этом Q =const.

Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по 10модулю и направлению.

2. 01Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Ох) равна нулю:

Тогда из уравнений (4`) следует, что при этом Q = const.

Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная.

Эти результаты и выражают закон сохранения количества движения системы. Из них следует, что внутренние силы изменить суммарное количество движения системы не могут.

Рассмотрим некоторые примеры:

· Я в л е н и е о т д а ч и и л и о т к а т а. Если рассматривать винтовку и пулю как одну систему, то давление пороховых газов при выстреле будет силой внутренней. Эта сила не может изменить суммарное количество движения системы. Но так как пороховые газы, действуя на пулю, сообщают ей некоторое количество движения, направленное вперед, то они одновременно должны сообщит винтовке такое же количество движения в обратном направлении. Это вызовет движение винтовки назад, т.е. так называемую отдачу. Аналогичное явление получается при стрельбе из орудия (откат).

· Р а б о т а г р е б н о г о в и н т а (п р о п е л л е р а). Винт сообщает некоторой массе воздуха (или воды) движение вдоль оси винта, отбрасывая эту массу назад. Если рассматривать отбрасываемую массу и самолет (или судно) как одну систему, то силы взаимодействия винта и среды как внутренние не могут изменить суммарное количество движения этой системы. Поэтому при отбрасывании массы воздуха (воды) назад самолет (или судно) получают соответствующую скорость движения вперед, такую, что общее количество движения рассматриваемой системы остается равным нулю, так как оно было нулем до начала движения.

Аналогичный эффект достигается действием весел или гребных колес.

· Р е а к т и в н о е д в и ж е н и е. В реактивном снаряде (ракете) газообразные продукты горения топлива с большой скоростью выбрасываются из отверстия в хвостовой части ракеты (из сопла реактивного двигателя). Действующие при этом силы давления будут силами внутренними и они не могут изменить суммарное количество движения системы ракета- пороховые газы. Но так как вырывающиеся газы имеют известное количество движения,направленное назад, то ракета получает при этом соответствующую скорость движения вперед.

Теорема моментов относительно оси.

Рассмотрим материальную точку массы m , движущуюся под действием силы F . Найдем для неё зависимость между моментом векторов mV и F относительно какой-нибудь неподвижной оси Z.

m z (F) = xF - уF (7)

Аналогично для величины m (mV) , если вынести m за скобку будет

m z (mV) = m(хV - уV) (7`)

Беря от обеих частей этого равенства производные по времени, находим

В правой части полученного выражения первая скобка равна 0, так как dx/dt=V и dу /dt = V , вторая же скобка согласно формуле (7) равна

m z (F) , так как по основному закону динамики:

Окончательно будем иметь (8)

Полученное уравнение выражает теорему моментов относительно оси: производная по времени от момента количества движения точки относительно какой-нибудь оси равна моменту действующей силы относительно той же оси. Аналогичная теорема имеет место и для моментов относительно любого центра О.

Количество движения системы, как векторная величина, определяется формулами (4.12) и (4.13).

Теорема. Производная от количества движения системы по времени равна геометрической сумме всех действующих на нее внешних сил.

В проекциях декартовые оси получим скалярные уравнения.

Можно записать векторное

(4.28)

и скалярные уравнения

Которые выражают теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов за тот же промежуток времени. При решении задач чаще используются уравнения (4.27)

Закон сохранения количества движения

Теорема об изменении кинетического момента

Теорема об изменении момента количества движения точки относительно центра: производная по времени от момента количества движения точки относительно неподвижного центра равна векторному моменту, действующей на точку силы относительно того же центра.

Или (4.30)

Сравнивая (4.23) и (4.30), видим, что моменты векторов и связаны такой же зависимостью, какой связаны сами векторы и (рис. 4.1). Если спроектировать равенство на ось , проходящую через центр О, то получим

(4.31)

Это равенство выражает теорему момента количества движения точки относительно оси.

Рис. 4.1.

Теорема об изменении главного момента количества движения или кинетического момента механической системы относительно центра: производная по времени от кинетического момента системы относительно некоторого неподвижного центра равно сумме моментов всех внешних сил относительно того же центра.

(4.32)

Если спроектировать выражение (4.32) на ось , проходящей через центр О, то получим равенство, характеризующее теорему об изменении кинетического момента относительно оси.

(4.33)

Подставляя (4.10) в равенство (4.33) можно записать дифференциальное уравнение вращающегося твердого тела (колес, осей, валов, роторов и т.д.) в трех формах.

(4.34)

(4.35)

(4.36)

Таким образом, теорему об изменении кинетического момента целесообразно использовать для исследования весьма распространенного в технике движения твердого тела, его вращения вокруг неподвижной оси.

Закон сохранения кинетического момента системы

1. Пусть в выражении (4.32) .

Тогда из уравнения (4.32) следует, что , т.е. если сумма моментов всех приложенных к системе вешних сил относительно данного центра равно нулю, то кинетический момент системы относительно этого центра будет численно и по направлению будет постоянен.

2. Если , то . Таким образом, если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то кинетический момент системы относительно этой оси будет величиной постоянной.

Эти результаты выражают собой закон сохранения кинетического момента.

В случае вращающегося твердого тела из равенства (4.34) следует, что, если , то . Отсюда приходим к следующим выводам:

Если система неизменяема (абсолютно твердое тело), то , следовательно, и и твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью.

Если система изменяема, то . При увеличении (тогда отдельные элементы системы удаляются от оси вращения) угловая скорость уменьшается, т.к. , а при уменьшении увеличивается, таким образом, в случае изменяемой системы с помощью внутренних сил можно изменить угловую скорость.

Вторая задача Д2 контрольной работы посвящена теореме об изменении кинетического момента системы относительно оси.

Задача Д2

Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R, где R = 1,2м) массой кг вращается с угловой скоростью вокруг вертикальной оси z, отстоящей от центра масс C платформы на расстоянии OC = b (рис. Д2,0 – Д2,9, табл. Д2); размеры для всех прямоугольных платформ показаны на рис. Д2,0а (вид сверху).

В момент времени по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой кг по закону , где s выражено в метрах, t - в секундах. Одновременно на платформы начинает действовать пара сил с моментом M (задан в ньютонометрах; при M < 0 его направление противоположно показанному на рисунках).

Определить, пренебрегая массой вала, зависимость т.е. угловую скорость платформы, как функцию времени.

На всех рисунках груз D показан в положении, при котором s > 0 (когда s < 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии OC = b от центра C.

Указания. Задача Д2 – на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость груза складывается из относительной и переносной скоростей, т.е. . Поэтому и количество движения этого груза . Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой ; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д2.

При решении задачи полезно изобразить на вспомогательном чертеже вид на платформу сверху (с конца z), как это сделано на рис. Д2,0,а – Д2,9, а.

Момент инерции пластины с массой m относительно оси Cz, перпендикулярной пластине и проходящей через ее центр масс, равен: для прямоугольной пластины со сторонами и

;

Для круглой пластины радиуса R

Номер условия	b	s = F(t)	M
	R R/2 R R/2 R R/2 R R/2 R R/2	-0.4 0.6 0.8 10 t 0.4 -0.5t -0.6t 0.8t 0.4 0.5	4t -6 -8t -9 6 -10 12

	Рис. Д2.0		Рис. Д2.0а

	Рис. Д2.1		Рис. Д2.1а

	Рис. Д2.2		Рис. Д2.2а

	Рис. Д2.3		Рис. Д2.3а

	Рис. Д2.4
		Рис. Д2.4а

		Рис. Д2.5а
	Рис. Д2.5

	Рис. Д2.6		Рис. Д2.6а

	Рис. Д2.7		Рис. Д2.7а

	Рис. Д2.8		Рис. Д2.8а

	Рис. Д2.9		Рис. Д2.9а

	Рис. Д2

Пример Д2 . Однородная горизонтальная платформа (прямоуголь­ная со сторонами 2l и l), имеющая массу жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угло­вой скоростью (рис. Д2а). В момент времени на вал начинает действовать вращающий момент М, направленный противо­положно ; одновременно груз D массой , находящийся в желобе АВ в точке С, начинает двигаться по желобу (под действием внутрен­них сил) по закону s = CD = F(t).

Дано: m 1 = 16 кг, т 2 = 10 кг, l = 0,5 м, = 2 , s = 0,4t 2 (s - в метрах, t - в секундах), М = kt, где k =6 Нм/с. Опре­делить: - закон изменения угловой скорости платформы.

Решение. Рассмотрим механическую систему, состоящую из плат­формы и груза D. Для определения w применим теорему об изменении кинетического момента системы относительно оси z:

(1)

Изобразим действующие на систему внешние силы: силы тяжести реакции и вращающий момент M. Так как силы и параллельны оси z, а реакции и эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление (т. е. против хода часовой стрелки), получим и уравнение (1) примет такой вид.

Состоящую из n материальных точек. Выделим из этой системы некоторую точку M j с массой m j . На эту точку, как известно, действуют внешние и внутренние силы .

Приложим к точке M j равнодействующую всех внутренних сил F j i и равнодействующую всех внешних сил F j e (рисунок 2.2). Для выделенной материальной точки M j (как для свободной точки) запишем теорему об изменении количества движения в дифференциальной форме (2.3):

Запишем аналогичные уравнения для всех точек механической системы (j=1,2,3,…,n) .

Рисунок 2.2

Сложим почленно все n уравнений:

∑d(m j ×V j)/dt = ∑F j e + ∑F j i , (2.9)

d∑(m j ×V j)/dt = ∑F j e + ∑F j i . (2.10)

Здесь ∑m j ×V j =Q – количество движения механической системы;
∑F j e = R e – главный вектор всех внешних сил, действующих на механическую систему;
∑F j i = R i =0 – главный вектор внутренних сил системы (по свойству внутренних сил он равен нулю).

Окончательно для механической системы получаем

dQ/dt = R e . (2.11)

Выражение (2.11) представляет собой теорему об изменении количества движения механической системы в дифференциальной форме (в векторном выражении): производная по времени от вектора количества движения механической системы равна главному вектору всех внешних сил, действующих на систему .

Проецируя векторное равенство (2.11) на декартовы оси координат, получаем выражения для теоремы об изменении количества движения механической системы в координатном (скалярном) выражении:

dQ x /dt = R x e ;

dQ y /dt = R y e ;

dQ z /dt = R z e , (2.12)

т.е. производная по времени от проекции количества движения механической системы на какую-либо ось равна проекции на эту ось главного вектора всех действующих на эту механическую систему внешних сил .

Умножая обе части равенства (2.12) на dt , получим теорему в другой дифференциальной форме:

dQ = R e ×dt = δS e , (2.13)

т.е. дифференциал количества движения механической системы равен элементарному импульсу главного вектора (сумме элементарных импульсов) всех внешних сил, действующих на систему .

Интегрируя равенство (2.13) в пределах изменения времени от 0 до t , получаем теорему об изменении количества движения механической системы в конечной (интегральной) форме (в векторном выражении):

Q — Q 0 = S e ,

т.е. изменение количества движения механической системы за конечный промежуток времени равно полному импульсу главного вектора (сумме полных импульсов) всех внешних сил, действующих на систему за тот же промежуток времени .

Проецируя векторное равенство (2.14) на декартовы оси координат, получим выражения для теоремы в проекциях (в скалярном выражении):

т.е. изменение проекции количества движения механической системы на какую-либо ось за конечный промежуток времени равно проекции на эту же ось полного импульса главного вектора (сумме полных импульсов) всех действующих на механическую систему внешних сил за тот же промежуток времени .

Из рассмотренной теоремы (2.11) – (2.15) вытекают следствия:

1. Если R e = ∑F j e = 0 , то Q = const – имеем закон сохранения вектора количества движения механической системы: если главный вектор R e всех внешних сил, действующих на механическую систему, равен нулю, то вектор количества движения этой системы остается постоянным по величине и направлению и равным своему начальному значению Q 0 , т.е. Q = Q 0 .
2. Если R x e = ∑X j e =0 (R e ≠ 0) , то Q x = const – имеем закон сохранения проекции на ось количества движения механической системы: если проекция главного вектора всех действующих на механическую систему сил на какую-либо ось равна нулю, то проекция на эту же ось вектора количества движения этой системы будет величиной постоянной и равной проекции на эту ось начального вектора количества движения, т.е. Q x = Q 0x .

Дифференциальная форма теоремы об изменении количества движения материальной системы имеет важные и интересные приложения в механике сплошной среды. Из (2.11) можно получить теорему Эйлера.

Так как масса точки постоянна, а ее ускорение то уравнение (2), выражающее основной закон динамики, можно представить в виде

Уравнение (32) выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил

Пусть движущаяся точка имеет в момент времени скорость а в момент - скорость Умножим тогда обе части равенства (32) на и возьмем от них определенные интегралы. При этом справа, где интегрирование идет по времени, пределами интеграла будут а слева, где интегрируется скорость, пределами интеграла будут соответствующие значения скорости

Так как интеграл от равен то в результате получим

Стоящие справа интегралы, как следует из формулы (30), представляют собой импульсы действующих сил. Поэтому окончательно будет

Уравнение (33) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.

При решении задач вместо векторного уравнения (33) часто пользуются уравнениями в проекциях. Проектируя обе части равенства (33) на координатные оси, получим

В случае прямолинейного движения, происходящего вдоль оси теорема выражается первым из этих уравнений.

Решение задач. Уравнения (33) или (34) позволяют, зная как при движении точки изменяется ее скорость, определить импульс действующих сил (первая задача динамики) или, зная импульсы действующих сил, определить, как изменяется при движении скорость точки (вторая задача динамики). При решении второй задачи, когда заданы силы, надо вычислить их импульсы, Как видно из равенств (30) или (31), это можно сделать лишь тогда, когда силы постоянны или зависят только от времени.

Таким образом, уравнения (33), (34) можно непосредственно использовать для решения второй задачи динамики, когда в задаче в число данных и искомых величин входят: действующие силы, время движения точки и ее начальная и конечная скорости (т. е. величины ), причем силы должны быть постоянными или зависящими только от времени.

Задача 95. Точка, масса которой кг, движется по окружности с численно постоянной скоростью Определить импульс действующей на точку силы за время, в течение которого точка проходит четверть окружности

Решение. По теореме об изменении количества движения Строя геометрически разность этих количеств движения (рис. 222), находим из полученного прямоугольного треугольника

Но по условиям задачи следовательно,

Для аналитического подсчета можно, используя первые два из уравнений (34), найти

Задача 96. Грузу, имеющему массу и лежащему на горизонтальной плоскости, сообщают (толчком) начальную скорость Последующее движение груза тормозится постоянной силой F. Определить, через сколько времени груз остановится,

Решение. По данным задачи видно, что для определения времени движения можно воспользоваться доказанной теоремой. Изображаем груз в произвольном положении (рис. 223). На него действуют сила тяжести Р, реакция плоскости N и тормозящая сила F. Направляя ось в сторону движения, составляем первое из уравнений (34)

В данном случае - скорость в момент остановки), а . Из сил проекцию на ось дает только сила F. Так как она постоянна, то где - время торможения. Подставляя все эти данные в уравнение (а), получаем откуда искомое время

Просмотр: эта статья прочитана 14066 раз

Pdf Выберите язык... Русский Украинский Английский

Краткий обзор

Полностью материал скачивается выше, предварительно выбрав язык

Количество движения

Количество движения материальной точки - векторная величина, равная произведению массы точки на вектор ее скорости.

Единицей измерения количества движения является (кг м/с).

Количество движения механической системы - векторная величина, равная геометрической сумме (главному вектору) количества движения механической системы равняется произведению массы всей системы на скорость ее центра масс.

Когда тело (или система) движется так, что ее центр масс неподвижен, то количество движения тела равняется нулю (например, вращение тела вокруг неподвижной оси, проходящей через центр масс тела).

В случае сложного движения, количество движения системы не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения характеризует только поступательное движение системы (вместе с центром масс).

Импульс силы

Импульс силы характеризует действие силы за некоторый промежуток времени.

Импульс силы за конечный промежуток времени определяется как интегральная сумма соответствующих элементарных импульсов.

Теорема об изменении количества движения материальной точки

(в дифференциальной форм е ):

Производная по времени от количества движения материальной точки равна геометрической сумме действующих на точки сил.

(в интегральной форме ):

Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за этот промежуток времени.

Теорема об изменении количества движения механической системы

(в дифференциальной форме ):

Производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.

(в интегральной форме ):

Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов внешних сил, действующих на систему за этот промежуток времени.

Теорема позволяет исключить из рассмотрения заведомо неизвестные внутренние силы.

Теорема об изменении количества движения механической системы и теорема о движении центра масс являются двумя разными формами одной теоремы.

Закон сохранения количества движения системы

1. Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным по направлению и по модулю.
2. Если сумма проекций всех действующих внешних сил на любую произвольную ось равна нулю, то проекция количества движения на эту ось является величиной постоянной.

Выводы :

1. Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.
2. Теорема об изменении количества движения механической системы не характеризует вращательное движение механической системы, а только поступательное.

Приведен пример: Определить количество движения диска определенной массы, если известна его угловая скорость и размер.

Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.

Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.

Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается

Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается

Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы

Определение скорости и ускорения точки по заданным уравнениям движения
Пример решение задачи на определение скорости и ускорения точки по заданным уравнениям движения

Определение скоростей и ускорений точек твердого тела при плоскопараллельном движении
Пример решения задачи на определение скоростей и ускорений точек твердого тела при плоскопараллельном движении

Определение усилий в стержнях плоской фермы
Пример решения задачи на определение усилий в стержнях плоской фермы методом Риттера и методом вырезания узлов

Применение теоремы об изменении кинетического момента
Пример решения задачи на применение теоремы об изменении кинетического момента для определения угловой скорости тела, совершающего вращение вокруг неподвижной оси.