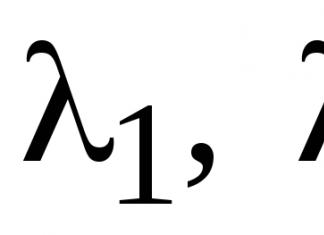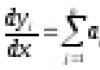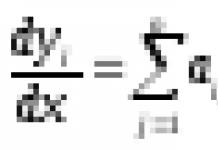Зачем нужна производная в жизни. Применение производной в физике, технике, биологии, жизни

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Всероссийский конкурс исследовательских работ учащихся

"ЮНОСТЬ, НАУКА, КУЛЬТУРА”

Творческая работа

Тема: "Применение производной в различных областях науки"

Калужский Михаил МБОУ "СОШ № 60 им. В. Завьялова"

Научный руководитель:

Минина М.Н.

г. Барнаул 2013/2014

Оглавление

Введение
Глава I
1.1 Исторические сведения
Глава II . Применение физического смысла производной при решении физических задач
1.1 Производная в механике
Глава III . Решение химических и биологических задач с помощью производной
3.1 Производная в химии
3.2 Производная в биологии
Глава IV . Решение задач с географическим, экономическим содержанием
4.1 Производная в географии
4.2 Производная в экономике
Заключение
Приложение

Введение

Тема "Производная функции" считается самой сложной в курсе школьной математики. Однако, "сложность" этой темы заключается в непонимании учащимися её нужности. Область применения производной остается непознанной даже студентам вузов. В связи с этим я решил провести опрос.

Смысл производной	Область применения дифференцированного исчисления	Нужна ли в жизни	Нужна ли в профессиональной деятельности
Геометрический	Строительство, экономика, высшая математика
Геометрический
	Строительство
	Математика
Физический, геометрический, алгебраический
Геометрический, физический
Физический
Геометрический	Математика

Данный опрос показал, что большинство людей не имеют полного представления о производной и обширной области её применения. Моя работа раздвигает рамки обыденного, она дает возможность разобраться в теме "производная функции", понять что производная встречается повсюду и очень важно знать что это такое и как это устроено.

производная функция математика наука

Глава I

1.1 Исторические сведения

Производная - одно из фундаментальных понятий математики. Оно возникло в 18 веке. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали теорию дифференциального исчисления.

Исаак Ньютон (1643-1727) - один из создателей дифференциального исчисления. Главный его труд - "Математические начала натуральной философии". - оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.

Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Г.В. Лейбниц. (1646-1716) - создатель Берлинской академии наук. Основоположник дифференциального исчисления, ввёл большую часть современной символики математического анализа.

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл. В самом деле для любой функции y=f (x) в системе координат, на ее области определения можно построить график. Если взять точку на оси абсцисс то, соответственно этой точки можно найти точку на графике функции. В этой точке может быть построена касательная, которая образует с положительным направлением оси абсцисс угол б.

Но это не говорит о том, …

…что до них эти вопросы не изучались. Задолго до этого Архимед (287 до н.э. - 212 до н. э) не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.

Эпизодически понятие касательной встречалось в работах итальянского математика И. Тартальи (1499-1557).

В 17в. на основе учения Г. Галилея (1564-1642) активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р. Декарта (1596-1650), французского математика Ж. Роберваля (1602-1675), английского учёного Д. Грегори (1638-1675), в работах И. Барроу (1630-1677).

Большой вклад в изучение дифференциального исчисления внесли Лопиталь (1661-1704), Бернулли (1744-1807), Лагранж (1736-1813), Гаусс (1777-1855), Коши (1789-1857). Необходимо сказать, что ни Ньютон ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа.

Глава II. Применение физического смысла производной при решении физических задач

Применение производной в физике очень обширно. Рассмотрим несколько примеров применения производной в физических задачах.

1.1 Производная в механике

Механическое движение - это изменение положения тела в пространстве относительно других тел с течением времени.

Основной характеристикой механического движения служит скорость.

Алгоритм нахождения скорости тела с помощью производной.

Если закон движения тела задан уравнением s = s (t), то для нахождения мгновенной скорости тела в какой-нибудь определенный момент времени надо:

1. Найти производную s" = f " (t).

2. Подставить в полученную формулу заданное значение времени.

Задание. Автомобиль приближается к мосту со скоростью 72 км/ч. У моста висит дорожный знак "36 км/ч". За 7 сек до въезда на мост, водитель нажал на тормозную педаль. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой s=20t-tІ

Да, т.к. скорость через 7 сек. будет равна 6м/с (21,6 км/ч).

1.2 Производная в электротехнике

В наших домах, на транспорте, на заводах: всюду работает электрический ток.

Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Задание.

Заряд, протекающий через проводник, меняется по закону

Найти силу тока в момент времени t=5 cек.

Сила тока равна 2 А

Сила есть производная работы по перемещению,

т.е. F=A / (x )

Теплоемкость - есть производная теплоты по температуре, т.е. C (t) = Q / (t)

d (l ) =m / (l ) - линейная плотность

K (t) = l / (t) - коэффициент линейного расширения

щ (t) = ц / (t) - угловая скорость

а (t) = щ / (t) - угловое ускорение

N (t) = A / (t) - мощность

Задание : теплота .

1. Пусть Q (t) количество теплоты, которое необходимо для нагревания тела массой 1 кг от 0 0 С до температуры t 0 (по Цельсию), известно, что в диапазоне 0 0 до 95 0 , формула Q (t) = 0,396t+2,08110 -3 t 2 -5,02410 -7 t 3 дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.

Решение . C (t) = Q / (t) = 0,396 + 4,16210 - 3 t - 15,07210 - 7 t 2

Глава III. Решение химических и биологических задач с помощью производной

3.1 Производная в химии

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Химия - это наука о веществах, о химических превращениях веществ.

Химия изучает закономерности протекания различных реакций.

Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.

Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Если C (t ) - закон изменения количества вещества, вступившего в химическую реакцию, то скорость v (t ) химической реакции в момент времени t равна производной:

Предел этого отношения при стремлении Дt к нулю - есть скорость химической реакции в данный момент времени V (t) = c ` (t)

Найти скорость реакции в момент времени t = 10 сек, если концентрация исходного продукта меняется по закону

3.2 Производная в биологии

Популяция - это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Задача по биологии.

По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t.

Понятие на языке биологии	Обозначение	Понятие на языке математики
Численность в момент времени t 1
Интервал времени		Приращение аргумента
Изменение численности популяции	X = x (t 2) - x (t 1)	Приращение функции
Скорость изменения численности популяции		Отношение приращения функции к приращению аргумента
Относительный прирост в данный момент		Производная

Глава IV. Решение задач с географическим, экономическим содержанием

4.1 Производная в географии

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N (t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Пусть у = у (t) - численность населения.

Рассмотрим прирост населения за t = t-t 0

y = k y t,

где к = к р - к с - коэффициент прироста (к р - коэффициент рождаемости,

к с - коэффициент смертности)

y: t=k y

При t0 получим lim y/ t=у"

у"= к у

4.2 Производная в экономике

Современный экономист должен хорошо владеть количественными методами анализа. К такому выводу нетрудно прийти практически с самого начала изучения экономической теории. При этом важны как знания традиционных математических курсов (математический анализ, линейная алгебра, теория вероятностей), так и знания, необходимые непосредственно в практической экономике и экономических исследованиях (математическая и экономическая статистика, теория игр, эконометрика и др.).

Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.

Ф. Энгельс в своё время заметил, что "лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но и процессы: движение". Поэтому целью моей работы является выяснить, каков экономический смысл производной, какие новые возможности для экономических исследований открывает дифференциальное исчисление, а также исследовать применение производной при решении различных видов задач по экономической теории.

П (t) = х / (t) - производительность труда, где х (t) - объем продукции J (x) = y / (x) - предельные издержки производства, где y - издержки производства в зависимости от объема выпускаемой продукции x.

Задание.

Оборот предприятия за истекший год описывается через функцию U (t) =0,15tі - 2tІ + 200, где t - месяцы, U-миллионы.

Исследуйте оборот предприятия за 9 и 10 месяцы.

Решение. Исследуем оборот предприятия с помощью производной: U" (t) =0,45tІ - 4t

Меньший оборот был на девятом месяце - 0,45. На 10 месяце - 5.

Заключение

Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д. Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

Список используемых источников

1. http://ru. wikipedia.org/

2. http://www.calameo.com/

3. http://rudocs. exdat.com/

4. http://www.rae.ru/

5. А. Фуше "Педагогики математики"

Приложение

Го м тфрид Ви м льгельм Ле м йбниц (нем. Gottfried Wilhelm Leibniz); 21 июня (1 июля) 1646 - 14 ноября 1716) - немецкий философ, логик,математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии наук

Сэр Исаа м к Нью м тон (англ. Sir Isaac Newton, 4 января 1643 года - 31 марта 1727 года) - английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда "Математические начала натуральной философии", в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета и многие другие математические и физические теории.

Размещено на Allbest.ru

...

Подобные документы

Понятие производной, правила её применения, геометрический и физический смысл производной. Применение производной в науке и технике и о решении задач в этой области. Актуальность дифференциального исчисления в связи с научно-техническим прогрессом.

реферат , добавлен 17.05.2009

Определение производной, понятие интеграла и определение предела функции. Дифференцирование и применение производной к решению задач. Исследование функции, вычисление интегралов и доказательство неравенств. Порядок вычисления пределов, Правило Лопиталя.

курсовая работа , добавлен 01.06.2014

Производная функция. Касательная к кривой. Геометрический смысл производной. Производные от элементарных функций. Изучение функций с помощью производной. Максимум и минимум функции. Точки перегиба. Дифференциал.

статья , добавлен 11.01.2004

Осуществление интерполяции с помощью полинома Ньютона. Уточнение значения корня на заданном интервале тремя итерациями и нахождение погрешности вычисления. Применение методов Ньютона, Сампсона и Эйлера при решении задач. Вычисление производной функции.

контрольная работа , добавлен 02.06.2011

Предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится к нулю. Обозначения производной. Понятие дифференцирования функции производной и ее геометрический смысл. Уравнение касательной к кривой.

презентация , добавлен 21.09.2013

Геометрический смысл производной. Анализ связи между непрерывностью и дифференцируемостью функции. Производные основных элементарных функций. Правила дифференцирования. Нахождение производной неявно заданной функции. Логарифмическое дифференцирование.

презентация , добавлен 14.11.2014

Поиск производной сложной функции как равной производной функции по промежуточному аргументу, умноженной на его производную по независимой переменной. Теорема о связи бесконечно малых величин с пределами функций. Правило дифференцирования сложной функции.

презентация , добавлен 21.09.2013

Определение производной функции, геометрический смысл ее приращения. Геометрический смысл заданного отношения. Физический смысл производной функции в данной точке. Число, к которому стремится заданное отношение. Анализ примеров вычисления производной.

презентация , добавлен 18.12.2014

Некоторые применения производной. Использование основных теорем дифференциального исчисления к доказательству неравенств. Первообразная и интеграл в задачах элементарной математики. Монотонность интеграла. Некоторые классические неравенства.

курсовая работа , добавлен 11.01.2004

Понятие производной, ее геометрический и физический смысл, дифференциал. Исследование функций и построение графиков. Разложение на множители, упрощение выражений. Решение неравенств, систем уравнений и доказательство тождеств. Вычисление пределов функции.

Тема «Производная» - это один из важнейших разделов курса математического анализа, так как это понятие является основным в дифференциальном исчислении и служит исходной базой при построении интегрального исчисления. Но часто, ученики, сталкиваясь с этим понятием в первый раз, не понимают для чего нужно его изучать. Они не видят практического применения этой темы. Поэтому данный проект «Применение производной» направлен на то, чтобы ученики выяснили, зачем нужно изучать производную, где можно использовать знания, связанные с производной в жизни, а также в других предметах.

Задумаемся над вопросом: А так ли часто в нашей речи мы используем слово - производная?

Скачать:

Предварительный просмотр:

https://accounts.google.com

Подписи к слайдам:

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу. Их, великих, загадочность окружающего мира притягивала, а исследование увлекало.

О великом Ньютоне! Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. А.Поуг. Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления. Главный его труд- «Математические начала натуральной философии».-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания. Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

О Лейбнице. «Предупреждаю, чтобы остерегались отбрасывать dx ,-ошибка, которую часто допускают и которая препятствует продвижению вперёд». Г.В.Лейбниц. (1646-1716) Создатель Берлинской академии наук. Основоположник дифференци - ального исчисления, ввёл большую часть современной символики матема - тического анализа. Лейбниц пришёл к понятию производной решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Николо Тарталья Галилео Галилей Рене Декарт Роберьваль Барроу

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

«Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.»

С какой силой давит на землю кобра длиной L и массой M, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v? Пусть за время Δt голова змеи поднялась на Δl , центр тяжести поднялся на высоту (1/2) Δl . Тогда скорость движения центра масс vц.м = (1/2)v. Изменение импульса змеи ΔP = Δmvц.м = FΔt , где Δt − время движения массы Δm . Поскольку Δm = (m/l) vΔt , то ΔP = (m/l) vΔt (v/2) = mv2/(2l) = FΔt . Тогда сила давления на землю будет равна: F = mv2/(2l) + mg . Так как змея поднимается вверх со скоростью v, то центр тяжести змеи поднимается вверх, обеспечивая добавочную к силе тяжести силу давления F, которую мы и рассчитаем.

Кривые роста знаний. “Он очень мало знает, но у него положительная производная”.

Предварительный просмотр:

Подписи к слайдам:

Презентацию подготовила: Егорова Дарья. Предмет: Алгебра Преподаватель: Орлова Ирина Анатольевна П рименение производной в физике

Направление производной в физике: Скорость материальной точки Мгновенная скорость как физический смысл производной Мгновенное значение силы переменного тока Мгновенное значение ЭДС электромагнитной индукции Максимальная мощность

Пусть зависимость пути s от времени t в данном прямолинейном движении материальной точки выражается уравнением s = f(t) и t 0 -некоторый момент времени. Рассмотрим другой момент времени t, обозначим ∆t = t - t 0 и вычислим приращение пути:∆ s = f(t 0 + ∆t) - f(t 0). Отношение ∆s / ∆t называют средней скоростью движения за время ∆t, протекшее от исходного момента t 0 . Скоростью называют предел этого отношения при ∆t → 0. Среднее ускорение неравномерного движения в интервале (t; t + ∆t) - это величина =∆v / ∆t. Мгновенным ускорением материальной точки в момент времени t будет предел среднего ускорения: То есть первая производная по времени (v"(t)). Скорость материальной точки

Задача. Зависимость пройденного телом пути от времени задается уравнением: s = A+Bt + Ct 2 +Dt 3 (C = 0,1 м / с, D = 0,03 м / с 2). Определить время после начала движения, через которое ускорение тела будет равно 2 м/с 2 . Решение: v(t) = s"(t) = B + 2Ct + 3Dt 2 ; a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2; 1,8 = 0,18t; t = 10 c Пример решения задач

Физический смысл производной x `(t) от непрерывной функции x (t) в точке t 0 – есть мгновенная скорость изменения величины функции, при условии, что изменение аргумента Δ t стремится к нулю. М гновенная скорость (величина пути, пройденного за мгновение) и есть производная величина от функции, описывающей путь самолёта по времени. Мгновенная скорость - это и есть физический смысл производной Мгновенная скорость как физический смысл производной

Согласно закону электромагнитной индукции: Например, при равномерном вращении проводящего контура площадью S в однородном магнитном поле с индукцией B c угловой скоростью магнитный поток, пронизывающий данный контур, изменяется по закону Тогда Мгновенное значение ЭДС электромагнитной индукции

Например, при электромагнитных колебаниях, возникающих в колебательном контуре заряд на обкладках конденсатора изменяется по закону Тогда Мгновенное значение силы переменного тока

Мощность тока Известно, что функция имеет экстремум (m ax или min) в точке в которой ее производная равна нулю. В данном случае Из решения полученного уравнения следует, что максимальная мощность при нагрузке может быть достигнута, если ее сопротивление R равно внутреннему сопротивлению источника тока r. Т.е. Максимальная мощность

Задач Решение задач

Задача. Вычислить количество теплоты, которое необходимо для того, чтобы нагреть 1 кг вещества от 0 градусов до t градусов (по Цельсию). Теплота

Решение Пусть Q=Q(t) . Рассмотрим малый отрезок , на этом отрезке Q=c(t) t c(t)= Q/t При t 0 lim Q/t =Q ′(t) t 0 c(t)=Q ′(t)

Заряд Задача. Вычислить силу тока I , который несет на себе заряд, заданный зависимостью q = q m cos ω 0 t (Кл) через поперечное сечение проводника.

Таким образом, применение производной довольно широко. В связи с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальным в решении как простых, так и сверхсложных задач.

Предварительный просмотр:

Подписи к слайдам:

ПРОИЗВОДНАЯ В БИОЛОГИИ

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Решение: Понятие на языке биологии Обозначение Понятие на языке математики Численность в момент времени t 1 x = x(t) Функция Интервал времени ∆t = t 2 – t 1 Приращение аргумента Изменение численности популяции ∆x = x(t 2) – x(t 1) Приращение функции Скорость изменения численности популяции ∆x/∆t Отношение приращения функции к приращению аргумента Относительный прирост в данный момент Lim ∆ x/∆t t 0 Производная Р = х ‘ (t)

Предварительный просмотр:

Подписи к слайдам:

Использование производной В экономике 1 Использование производной в экономике Проект подготовили: Ученики средней школы № 657 Кузнецова Александра Конькин Глеб Учитель: Орлова И.А.

Цели и задачи работы Узнать, что такое производная Изучить экономический смысл углового коэффициента Увидеть приложение скорости в экономической теории Прорешать задачи с помощью производной. 2

Производная и ее связь с экономикой Производной от функции у = f (x) в точке х 0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (D x → 0). Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление- аппарат для экономического анализа. Базовая задача экономического анализа- изучение связей экономических величин в виде функций. 3

Производная решает важные вопросы. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления. Также с помощью экстремума функции(производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки. Поэтому, производная важна для экономики, и мы рассмотрим основные аспекты. 4

Экономическое приложение производной В экономической теории используется понятие «маржинальный», то есть «предельный». Введение понятия в XIX веке позволило создать новый инструмент описания экономических явлений, посредством которого стало возможно решать научные проблемы. Экономическая теория Смита имела дело со средними величинами: средняя цена, средняя производительность труда. Но сложился иной подход. Существенные закономерности можно обнаружить и в области предельных величин. Предельные величины характеризуют не состояние, а изменение экономического объекта. Следовательно, производная выступает как интенсивность изменения экономического объекта. 5

Рассмотрим ситуацию: пусть y - издержки производства, а х - количество продукции, тогда x1 - прирост продукции, а y1 - приращение издержек производства. В этом случае производная выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции. Где: MC - предельные издержки (marginal costs); TC - общие издержки (total costs); Q - количество. 6 Решение задач. №1

№ 2. Производительность труда Через производную можно определить и производительность труда: Пусть функция u = u (t) выражает количество произведенной продукции u за время t . Необходимо найти производительность труда в момент tο . За период времени от tο до tο + Δt количество произведенной продукции изменится от значения uο = u (tο) до значения uο + Δu = u (tο + Δt). Тогда средняя производительность труда за этот период времени Zср = Δu: Δt . Очевидно, что производительность труда в момент tο можно определить как предельное значение средней производительности за период времени от tο до tο + Δt при Δt → 0, т.е. z = lim Zср = lim Δu/Δt = u "(t) при Δt →0 7

Задача по экономической теории. Предприятие производит Х единиц некоторой однородной продукции в месяц. Установлено, что зависимость финансовых накопления предприятия от объема выпуска выражается формулой f (x)=-0,02x^3+600x -1000. Исследовать потенциал предприятия. Функция исследуется с помощью производной. Получаем, что при Х=100 функция достигает максимума. Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению финансовых накоплений. Таким образом, задачи,решаемые с помощью производной, широко используются в производстве. 8

Предельный анализ в экономике. Эластичность функций Применение производной в экономике позволяет получать так называемые предельные характеристики экономических процессов. Анализ состояния и изменения экономического объекта - проблема, стоящая перед специалистами в этой области. Цель этого исследования - рассмотреть примеры применения предельных характеристик экономических процессов с помощью производной. Эластичность функции. Пусть дана функция y = f (x), для которой существует производная y " = f(x) . Эластичностью функции y = f (x) относительно переменной x называют предел E x (y) = x / y = . Эластичность относительно x - процентный прирост функции, соответствующий приращению независимой переменной на 1%. 9

Производственные издержки Производственные издержки - это денежное выражение затрат производственных факторов, используемых в производстве и реализации. Они бывают: постоянные - не зависимые от объема и структуры производства. переменные - зависят от объема производства. Средние или удельные - на единицу продукции Предельные или маржинальные - это отношение прироста переменных издержек к вызванному ими приросту продукции. 10

Ценовая эластичность спроса. Реакция величины спроса на изменение цены товара – это ценовая эластичность спроса. Спрос эластичен по цене, если процентное изменение объема спроса превышает процентное изменение цены. Если процентное изменение объема спроса отстает от процентного изменения цены, то спрос по цене неэластичен. Например, если все сорта растительного масла подорожают на 49 %, а объем спроса снизится только на 19%, то спрос на растительное масло неэластичен по цене. При эластичном спросе доход продавца и цена товара изменяются в противоположных направлениях. 11

Неэластичный спрос Если спрос на товар неэластичен, цены и доход изменяются в одном направлении. Данные величины измеряются формулой: где Е р D - эластичность спроса по цене; ДQd - относительное изменение спроса (в процентах); ДP - относительное изменение цены (в процентах). где Q 1 , Q 0 - величина спроса до и после изменения цены; P 1 , P 0 - цена до и после изменения. Е р D берут по модулю. С увеличением цены объем спроса снижается. 12

Д ополнительно. Информация о эластичности или неэластичности спроса на товар очень важна для предпринимателей, целью которых является увеличение дохода, или выручки от продажи товара, которую можно подсчитать, умножив цену одной единицы товара на количество реализованных товаров: Y = P*Q . Где Y - доход, или выручка от продажи товаров, P - цена единицы товара, Q - количество проданного товара. 13

Ценовая эластичность предложения ценовая эластичность предложения- это реакция на изменение цены со стороны производителей. Эластичность предложения определяет степень реагирования производителей различной продукции на цены. Ценовая эластичность предложение показывает, на сколько изменится в З процентом соотношении величина предложения при изменении цены товара (услуги) на 1%. Предложение эластично, если при изменении цены на 1% его объем изменится более чем на 1% Например, при повышении цены на мороженое на 10 % величина предложения его вырастет на 15% Предложение неэластично, если при изменении цены товара на 1 % объем его предложения изменится менее чем на 1 %. Например, если цена на нефть вырастет на 40 % , а объем предложения увеличится на 32 % 14

Формула для расчета Ц.Э.П. Показатель (коэффициент) ценовой эластичности предложения рассчитывается по формуле: где ∆Q – изменение величины предложения товара; ∆ р – изменение цены товара Если Е р S >1, то предложение эластично по цене т. е. величина предложения гибко реагирует на изменение цены Если Е р S = 1, то предложение с единичной эластичностью Если Е р S

Вывод: Э кономическое приложение производной помогает как экономистам и бизнесменам, так и обычным гражданам в распоряжении бюджетом. 16

17 Спасибо за внимание!!!

Предварительный просмотр:

Подписи к слайдам:

Производная и ее применение в алгебре

Понятие производной Пусть y = f (x) есть непрерывная функция аргумента x , определенная в промежутке (a ; b), и пусть х0 - произвольная точка этого промежутка Дадим аргументу x приращение ∆ x , тогда функция y = f (x) получит приращение ∆ y = f (x + ∆ x) - f (x). Предел, к которому стремится отношение ∆ y / ∆ x при ∆ x → 0, называется производной от функции f (x). y "(x)=

k = f ′(x o) = tg α – это угловой коэффициент касательной. f(x o) Касательная к графику дифференцируемой в точке х 0 функции f – это прямая, проходящая через точку (х о; f(x о)) и имеющая угловой коэффициент f ′ (х о). х у х о y = kx + b α y = f(x) 0

Приближенные вычисления f(x) ≈ f(x o) + f ′(x o)∆x (1) √ 1 + ∆x ≈ 1 + ∆x 1 2 (2) (1 + ∆x) n ≈ 1 + n∆x (3)

Общий вид уравнения касательной y = f ′(x o)(x – x o) + f(x o) Алгоритм составления уравнения касательной 1 о Находим значение функции в точке х о: f(x o) . 2 о Дифференцируем функцию: f′(x) . 3 о Находим значение производной в точке х о: f′(x o) . 4 о Подставляем эти данные в общее уравнения касательной: y = f′(x o)(x – x o) + f(x o) .

Правила дифференцирования и таблица производных

x o Максимум функции Точка х о называется точкой максимума функции f(x) , если существует такая окрестность точки х о, что для всех х ≠ х о из этой окрестности выполняется неравенство f(x)

Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Монотонность функций 1) Если f′(x) > 0 внутри промежутка I, то функция f возрастает на этом промежутке. 2) Если f′(x) 0  f(x) возрастает при х  R 2 о f(x) = – 2x 5 – 6x f ′(x) = – 10x 4 – 6

Алгоритм исследования функции на монотонность 1 о Дифференцируем функцию: f′(x) . 2 о Находим критические точки из уравнения: f′(x) = 0 . 3 о Решаем неравенства: f′(x) > 0 и f′(x)

Алгоритм исследования функции на экстремумы 1 о Дифференцируем функцию: f′(x) . 2 о Находим критические точки из уравнения: f′(x) = 0 . 3 о Решаем неравенства: f′(x) > 0 и f′(x)

Нахождение наибольшего и наименьшего значения функции на заданном отрезке 1 о Выясняем существование функции на данном отрезке . 2 о Дифференцируем функцию: f′(x) . 3 о Находим критические точки из уравнения: f′(x) = 0 . 4 о Отбираем те точки, которые принадлежат заданному промежутку . 5 о Находим значение функции в этих точках и на концах промежутка: f(a) ; f(b) ; f(x 1) ; f(x 2) ; и т. д. 6 о Выбираем среди полученных значений наибольшее или наименьшее.

Предварительный просмотр:

Подписи к слайдам:

Применение производной в географии.

ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ. Изучить математическую величину в сфере естественной науки, их связь. Просмотреть, какие процессы регулирует производная в географии. Решить задачу, которая пригодится и для переписи населения. Детская страничка: производная в картинках.

Производная помогает рассчитать: Некоторые значения в сейсмографии Особенности электромагнитного поля земли Радиоактивность ядерно- геоифзичексих показателей Многие значения в экономической географии Вывести формулу для вычисления численности населения на территории в момент времени t .

План местности.

Численность населения. Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N (t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Решение задач. №1 Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t . Пусть у = у(t)- численность населения. Рассмотрим прирост населения за  t = t - t 0  y = k y  t , где к = к р – к с –коэффициент прироста (к р – коэффициент рождаемости, к с – коэффициент смертности)  y:  t = k y При  t  0 получим lim  y /  t =у’.

Интерполяция. Интерполяцией называется приближенное вычисление значений функции по нескольким данным ее значениям. Интерполяция широко используется в картографии, геологии, экономике и других науках. Самым простым вариантом интерполяции является форма Лагранжа, но когда узловых точек много и интервалы между ними велики, либо требуется получить функцию, кривизна которой минимальна.

Интерполяционная формула Лагранжа. Пример:

Спасибо за внимание!!!

Предварительный просмотр:

Подписи к слайдам:

Производная в химии.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. Как используют производную в химии?

Например, инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства, а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. Поэтому в реальной жизни для решения производственных задач в медицинской, сельскохозяйственной и химической промышленности просто необходимо знать скорости реакций химических веществ.

Скоростью химической реакции в химии называется изменение концентрации реагирующих веществ в единицу времени или производная от концентрации реагирующих веществ по времени (на языке математике концентрация была бы функцией, а время – аргументом) Определение

Если P (t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v (t) химической реакции в момент времени t равна производной: V (t) = p ‘(t) Формула производной в химии

Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: р (t) = t 2 /2 + 3 t –3 (моль) Найти скорость химической реакции через 3 секунды. Пример задачи по химии:

р (t) = t 2 /2 + 3 t –3 (моль) 1. Найдем производную функции: Р ’(t) = t +3 2. Подставим значение t = 3 сек: P’(3) = 3 + 3 = 6 (моль/сек) Ответ: 6 Решение:

Понятие на языке химии Обозначение Понятие на языке математики Количество в- ва в момент времени t 0 p = p(t 0) Функция Интервал времени ∆t = t– t 0 Приращение аргумента Изменение количества в-ва ∆p= p(t 0 + ∆ t) – p(t 0) Приращение функции Средняя скорость химической реакции ∆p/∆t Отношение приращёния функции к приращёнию аргумента V (t) = p ‘(t)

Понятие производной очень важно в химии при определении скорости течения реакции. Заключение

Предварительный просмотр:

1. Введение.

2. История изучения производной

3. Применение производной в математике

4. Применение производной в физике

5. Применение производной в химии

6. Применение производной в экономике

7. Применение производной в биологии

8. Применение производной в географии

9. Заключение

ВВЕДЕНИЕ

Задумаемся над вопросом: А так ли часто в нашей речи мы используем слово - производная»? Обратимся к информационным источникам.

12.01.11 - Советская Россия

«Качество жизни и процветание – это производная не только от экономики. Можно все больше богатеть, но если неприятие действительности в обществе растет, благополучие обязательно падает», – таково авторитетное мнение директора Центра политических технологий Игоря Бунина.

27.12.10 - Полит.ру

Очевидно, что в обоих случаях можно увидеть результаты изменения демографической политики государства. Однако на данный момент нельзя сделать заключение о наличии или отсутствии синергетического эффекта от одновременного применения мер направленных на снижение смертности и повышение рождаемости.

09.01.11 - Woman.ru - интернет для женщин

Поэтому здесь все наоборот - эта тема главная в жизни человека. а все остальные второстепепенные производные и малозначительные по сравнению с главной. Так что Девочки, которые разговаривают об отношениях между Мужчиной и Женщиной разговаривают о самом Главном в жизни.

В интервью, опубликованном в декабре прошлого года журналом "Компания", владелец банка "Тинькофф Кредитные системы" назвал Александра Лебедева " производной коррупции, плотью от плоти коррупционной системы".

Актуальность темы “Производная в школьном курсе математики” следует из того, что человек в повседневной деятельности постоянно сталкивается с решением задач, которые могут быть полностью описаны с помощью функций на математическом языке, а между тем производная является мощным орудием исследования функций.

Цель исследования

распознавать, обследовать и разрешать проблемные ситуации из области математики, привлекая знания из разных областей науки;
самостоятельно, критически мыслить;
прогнозировать результаты;
практически применять полученные знания;
формировать навыки работы в команде, навыки публичного выступления;
расширять свои знания;
развивать аналитическое мышление;
приобрести навыки самостоятельной работы;
работать творчески, конструировать, моделировать, проектировать и т.д.
использовать определение производной при решении практических задач.

Задачи исследования

Как используется производная на практике? Как используется производная при решении физических, геометрических, экономических, географических задач?

Практическая значимость

Нужна ли производная для будущей профессии?

Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными

Применение производной для решения задач требует от учащихся нетрадиционного мышления. Следует отметить, что знание нестандартных методов и приемов решения задач способствует развитию нового, нешаблонного мышления, которое можно успешно применять также и в других сферах человеческой деятельность (вычислительная техника, экономика, физика, химия и т.д.) Это доказывает актуальность данной работы.

Целью работы было: изучение применения производной для решения задач по алгебре и началам анализа, физике, экономике; углубление и расширение знаний по теме «Производная». При изучении изменяющихся величин очень часто возникает вопрос о скорости, о быстроте происходящего изменения. Так мы говорим о скорости движения самолета, поезда, автобуса, ракеты, о скорости падения камня, вращения шкива и т.д. Можно говорить о скорости выполнения определенной работы, о скорости протекания химической реакции, о быстроте роста населения в данном городе. О скорости можно говорить по отношению к любой величине, которая изменяется с течением времени. Для всего этого используется понятие производной.

История изучения производной

Производная – одно из фундаментальных понятий математики.
Оно возникло в 18 веке. Независимо друг от друга И.Ньютон и
Г. Лейбниц разработали теорию дифференциального исчисления.

О Ньютоне.

Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. А.Поуг.
Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии».- оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Интересно: Исаак Ньютон был так же и богословом. Он написал труды о Святой Троице, а также толкование на книгу пророка Даниила. Интересно, что он высоко ценил именно свои богословские сочинения. Всегда, произнося имя Божие, Ньютон снимал шляпу.

О Лейбнице

«Предупреждаю, чтобы остерегались отбрасывать dx,-ошибка, которую часто допускают и которая препятствует продвижению вперёд». Г.В.Лейбниц. (1646-1716)
Создатель Берлинской академии наук. Основоположник дифференци- ального исчисления, ввёл большую часть современной символики матема- тического анализа.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл.
Но это не говорит о том, что до них эти вопросы не изучались.

Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.

Эпизодически понятие касательной встречалось в работах итальянского математика И.Тартальи .

В 17в. на основе учения Г.Галилея активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р.Декарта , французского математика Роберваля , английского учёного Д.Грегори , в работах И.Барроу .

Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс, Коши. Необходимо сказать, что ни Ньютон ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа.

(Презентация «История производной»)

Применение производной в математике

При исследовании функции очень часто приходится применять производные. Одной из основных задач при исследовании функции является определение промежутков возрастания и убывания функции. Это исследование очень легко можно произвести с помощью производной функции.

Признаки возрастания функции

Если f’(x)>0 на некотором промежутке, то функция f(x) возрастает на данном промежутке

Признак убывания функции

Если f’(x)

Строгое доказательство этих двух признаков изучается в курсе математического анализа, здесь же мы его приводить не будем.

Помимо, определения промежутков возрастания и убывания функции, с помощью производной при исследовании функции находят точки максимума и минимума этой функции.

Точки максимума и минимума функции называют еще точками экстремума.

Для отыскания точек экстремума существует отдельный признак.

Достаточное условие существование экстремума в точке.

Пусть f(x) некоторая дифференцируемая на интервале (a;b) функция. Точка х0 принадлежит этому интервалу и f’(x0)=0.

Тогда:

1. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «плюса» на «минус», тогда точка х0 является точкой максимума функции.
2. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «минуса» на «плюс», тогда точка х0 является точкой минимума функции

Геометрический смысл производной

Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x ) в этой точке.

Рассмотрим график функции y = f (x ):

Из рис.1 видно, что для любых двух точек A и B графика функции: xf(x0+ x)−f(x0)=tg , где - угол наклона секущей AB .
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B , то x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС .
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A .

Применение производной в физике.

Направление производной в физике:

Скорость материальной точки

Мгновенная скорость как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальная мощность

Скорость материальной точки.

Пусть зависимость пути s от времени t в данном прямолинейном движении

материальной точки выражается уравнением s = f(t) и t0 -некоторый

момент времени. Рассмотрим другой момент времени t, обозначим ∆t = t - t0 и вычислим приращение пути:∆s = f(t0 + ∆t) - f(t0). Отношение ∆s / ∆t называют средней скоростью движения за время ∆t, протекшее от исходного момента t0. Скоростью называют предел этого отношения при ∆t → 0.

Среднее ускорение неравномерного движения в интервале (t; t + ∆t) - это величин

То есть первая производная по времени (v"(t)).

Пример решения задач.

Задача. Зависимость пройденного телом пути от времени задается уравнением:

s = A+Bt + Ct2 +Dt3 (C = 0,1 м/с, D = 0,03 м/с2).

Определить время после начала движения, через которое ускорение тела будет равно 2 м/с2.

Решение:

v(t) = s"(t) = B + 2Ct + 3Dt2;

a(t) = v"(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 c .

Мгновенная скорость как физический

смысл производной.

Мгновенная скорость (величина пути, пройденного за мгновение) и есть производная величина от функции, описывающей путь самолёта по времени. Мгновенная скорость - это и есть физический смысл производной.

Мгновенное значение ЭДС электромагнитной индукции.

Согласно закону электромагнитной индукции:

Например, при равномерном вращении проводящего контура площадью S в однородном магнитном поле с индукцией B c угловой скоростью магнитный поток, пронизывающий данный контур, изменяется по закону

Тогда

Мгновенное значение силы переменного тока. Например, при электромагнитных колебаниях, возникающих в колебательном контуре заряд на обкладках конденсатора изменяется по закону

Тогда

Максимальная мощность.

Мощность тока

Известно, что функция имеет экстремум (max или min) в точке в которой ее производная равна нулю. В данном случае из решения полученного уравнения следует, что максимальная мощность при нагрузке может быть достигнута, если ее сопротивление R равно внутреннему сопротивлению источника тока r. Т.е.

Решение задач.

Теплота.

Задача. Вычислить количество теплоты, которое необходимо для того, чтобы нагреть 1 кг вещества от 0 градусов до t градусов (по Цельсию).

Решение. Пусть Q=Q(t).

Рассмотрим малый отрезок , на этом отрезке

DQ=c(t) Dt

c(t)= DQ/Dt

При Dt®0 lim DQ/Dt =Q′(t) Dt®0

c(t)=Q′(t)

Заряд.

Задача. Вычислить силу тока I, который несет на себе заряд, заданный зависимостью q=qm cos ω0t (Кл) через поперечное сечение проводника.

Производная в химии.

Как используют производную в химии?

Определение

Скоростью химической реакции в химии называется изменение концентрации реагирующих веществ в единицу времени

ИЛИ

производная от концентрации реагирующих веществ по времени (на языке математике концентрация была бы функцией, а время – аргументом).

Формула производной в химии

Если P(t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v(t) химической реакции в момент времени t равна производной:

V (t) = p ‘(t)

Пример задачи по химии:

Пусть количество вещества, вступившего в химическую реакцию, задается зависимостью:

р(t) = t2/2 + 3t –3 (моль)

Найти скорость химической реакции через 3 секунды.

Решение:

Найдем производную данной функции:

p(t) = t + 3

Подставим значение времени 3 с в производную:

p(3) = 3 + 3 = 6 (моль/с)

Ответ: 6 моль в секунду.

Понятие на языке химии Обозначение Понятие на языке математики

Количество в-ва в момент времени t0 p = p(t 0) Функция

Интервал времени ∆t = t– t0 Приращение аргумента

Изменение количества в-ва ∆p= p(t0+ ∆ t) – p(t0) Приращение функции

Средняя скорость химической реакции ∆p/∆t Отношение приращёния функции к приращёнию аргумента

Заключение

Таким образом, мы можем видеть, понятие производной очень важно в химии при

определении скорости течения реакций.

Производная в экономике

Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.

Ф.Энгельс в своё время заметил, что "лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но и процессы: движение". Поэтому целью моей работы является выяснить, каков экономический смысл производной, какие новые возможности для экономических исследований открывает дифференциальное исчисление, а также исследовать применение производной при решении различных видов задач по экономической теории.

Экономика – основа жизни, а в ней важное место

занимает дифференциальное исчисление- аппарат для экономического анализа. Базовая задача экономического анализа- изучение связей экономических величин в виде функций.

Производная решает важные вопросы.

В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию?

Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.

Также с помощью экстремума функции(производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

Поэтому, производная важна для экономики, и мы рассмотрим основные аспекты.

Экономическое приложение производной.

В экономической теории используется понятие «маржинальный», то есть «предельный». Введение понятия в XIX веке позволило создать новый инструмент описания экономических явлений,посредством которого стало возможно решать научные проблемы. Экономическая теория Смита имела дело со средними величинами: средняя цена, средняя производительность труда. Но сложился иной подход. Существенные закономерности можно обнаружить и в области предельных величин. Предельные величины характеризуют не состояние, а изменение экономического объекта. Следовательно, производная выступает как интенсивность изменения экономического объекта

Решение задач. №1

Рассмотрим ситуацию: пусть y - издержки производства, а х - количество продукции, тогда x1- прирост продукции, а y1 - приращение издержек производства.

В этом случае производная выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции.

Где:

MC - предельные издержки (marginal costs);

TC - общие издержки (total costs);

Q – количество

№ 2. Производительность труда

Через производную можно определить и производительность труда:

Пусть функция u = u(t) выражает количество произведенной продукции u за время t. Необходимо найти производительность труда в момент tο.

За период времени от tο до tο + Δt количество произведенной продукции изменится от значения uο = u(tο) до значения uο + Δu = u(tο + Δt). Тогда

средняя производительность труда за этот период времени Zср = Δu:Δt. Очевидно, что производительность труда в момент tο можно определить как предельное значение средней производительности за период времени от tο до tο + Δt при Δt → 0, т.е.

z = lim Zср = lim Δu/Δt = u"(t) при Δt→0

Задача по экономической теории.

Предприятие производит Х единиц некоторой однородной продукции в месяц. Установлено, что зависимость финансовых накопления предприятия от объема выпуска выражается формулой f(x)=-0,02x^3+600x -1000. Исследовать потенциал предприятия.

Функция исследуется с помощью производной. Получаем, что при Х=100 функция достигает максимума.

Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению финансовых накоплений.

Таким образом, задачи,решаемые с помощью производной, широко используются в производстве

Предельный анализ в экономике. Эластичность функций.

Применение производной в экономике позволяет получать так называемые предельные характеристики экономических процессов.

Анализ состояния и изменения экономического объекта - проблема, стоящая перед специалистами в этой области. Цель этого исследования - рассмотреть примеры применения предельных характеристик экономических процессов с помощью производной.

Эластичность функции. Пусть дана функция y = f(x), для которой существует производная y" =f(x) .Эластичностью функции y = f(x) относительно переменной x называют предел Ex (y) = x / y = .

Эластичность относительно x -процентный прирост функции, соответствующий приращению независимой переменной на 1 %.

Ценовая эластичность спроса.

Реакция величины спроса на изменение цены товара – это ценовая эластичность спроса.

Спрос эластичен по цене, если процентное изменение объема спроса превышает процентное изменение цены. Если процентное изменение объема спроса отстает от процентного изменения цены, то спрос по цене неэластичен. Например, если все сорта растительного масла подорожают

на 49 %, а объем спроса снизится только на 19%, то спрос на растительное масло неэластичен по цене.

При эластичном спросе доход продавца и цена товара изменяются в противоположных направлениях.

Неэластичный спрос.

Если спрос на товар неэластичен, цены и доход изменяются в одном направлении. Данные величины измеряются формулой:

где ЕрD - эластичность спроса по цене;

ДQd - относительное изменение спроса (в процентах);

ДP - относительное изменение цены (в процентах).

где Q1 , Q0 - величина спроса до и после изменения цены;

P1 , P0 - цена до и после изменения. ЕрD берут по модулю.

С увеличением цены объем спроса снижается

Дополнительно.

Информация о эластичности или неэластичности спроса на товар очень важна для предпринимателей, целью которых является увеличение дохода, или выручки от продажи товара, которую можно подсчитать, умножив цену одной единицы товара на количество реализованных товаров: Y = P*Q .

Где Y - доход, или выручка от продажи товаров, P - цена единицы товара, Q - количество проданного товара.

Ценовая эластичность предложения.

Ценовая эластичность предложения- это реакция на изменение цены со стороны производителей. Эластичность предложения определяет степень реагирования производителей различной продукции на цены.

Ценовая эластичность предложение показывает, на сколько изменится в З процентом соотношении величина предложения при изменении цены товара (услуги) на 1%.

Предложение эластично, если при изменении цены на 1% его объем изменится более чем на 1%

Например, при повышении цены на мороженое на 10 % величина предложения его вырастет на 15%

Предложение неэластично, если при изменении цены товара на 1 % объем его предложения изменится менее чем на 1 %.

Например, если цена на нефть вырастет на 40 % , а объем предложения увеличится на 32 %.

Формула для расчета Ц.Э.П.

Показатель (коэффициент) ценовой эластичности предложения рассчитывается по формуле:

где ∆Q – изменение величины предложения товара; ∆р – изменение цены товара

Если ЕрS >1, то предложение эластично по цене т. е. величина предложения гибко реагирует на изменение цены

Если ЕрS = 1, то предложение с единичной эластичностью

Если ЕрS

Вывод: Экономическое приложение производной помогает как экономистам и бизнесменам, так и обычным гражданам в распоряжении бюджетом.

Производная в географии.

Изучить математическую величину в сфере естественной науки, их связь.

Просмотреть, какие процессы регулирует производная в географии.

Решить задачу, которая пригодится и для переписи населения.

Некоторые значения в сейсмографии

Особенности электромагнитного поля земли

Радиоактивность ядерно- геоифзичексих показателей

Многие значения в экономической географии

Вывести формулу для вычисления численности населения на территории в момент времени t.

План местности.

Аналоговые (графические) копии карт и планов являются производными

от соответствующих цифровых оригиналов.

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Пусть у = у(t)- численность населения.

Рассмотрим прирост населения за  t = t-t 0

 y = k y  t, где к = к р – к с –коэффициент прироста (к р – коэффициент рождаемости,

к с – коэффициент смертности)

 y:  t=k y

При  t  0 получим lim  y/  t=у’

у’= к у

Производная в биологии

Понятие на языке биологии	Обозначение	Понятие на языке математики
Численность в момент времени t 1	x = x(t)	Функция
Интервал времени	∆t = t 2 – t 1	Приращение аргумента
Изменение численности популяции	∆x = x(t 2 ) – x(t 1 )	Приращение функции
Скорость изменения численности популяции	∆x/∆t	Отношение приращения функции к приращению аргумента
Относительный прирост в данный момент	Lim ∆x/∆t	Производная

Задача: По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t.

Решение проблемных поисковых задач.

1.С какой силой давит на землю кобра длиной L и массой M , когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v ? Применим 2-й закон Ньютона к движению змеи в целом. Сила N – сила реакции земли, равная по величине искомой силе давления змеи на землю, а импульс р = тv , т = уh - масса поднимающегося вертикального участка змеи высотой h , у = М/L , – заданная постоянная скорость подъёма. Соответственно N = Мg + dp/dt = Мg + у dh/dt v =Mg + yv 2 =M(g+ v 2 /L).

2. Пароход "Челюскин" в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли "Челюскин" на север и раздавили.

Вот описание катастрофы: "Крепкий металл корпуса поддался не сразу, – сообщал по радио начальник экспедиции О.Ю. Шмидт. – Видно было, как льдина вдавливается в борт, и как над ней листы обшивки пучатся, изгибаясь наружу. Лед продолжал медленное, но неотразимое наступление. Вспученные железные листы обшивки корпуса разорвались по шву. С треском летели заклепки. В одно мгновение левый борт парохода был оторван от носового трюма до кормового конца палубы…"

Почему произошла катастрофа?

Сила Р давления льда (рис. на доске – плакат) разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – a – угол наклона борта к вертикали. Q – сила трения льда о борт. Q = 0,2 R (0,2 – коэффициент трения). Если Q F, то трение мешает скольжению льдины, и лед может смять и продавить борт. 0,2R 0,2Q 110. Наклон бортов корабля к вертикали под углом a > 110 обеспечивает безопасное плавание во

Вывод:

Тема “Производная и ее применения” является одним из основных разделов начал математического анализа. При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Слова «производная» и «произошло» имеют похожие части слова, да и смысл похож: производная происходит от исходной функции (переложив на отношения человека: исходная функция - «мама», её производная «дочь»). Производная - часть математической науки, одно из её звеньев. Нет этого звена - прерваны связи между многими понятиями.

Производную применяют для исследования функции и построения ее графика, для нахождения наибольшего и наименьшего значений функции.

Оказывается также, что с помощью производной можно упрощать алгебраические и тригонометрические выражения, раскладывать на множители, доказывать тождества и неравенства и, даже, решать ворос о существовании корней квадратного уравнения.

Производная нужна также и с в экономике. В экономической теории активно используется понятие «маржинальный», что означает «предельный». Введение этого понятия в научный оборот в XIX веке позволило создать совершенно новый инструмент исследования и описания экономических явлений - инструмент, по средством которого стало возможно ставить и решать новый класс научных проблем.

Классическая экономическая теория Смита, Рикардо, Милля обычно имела дело со средними величинами: средняя цена, средняя производительность труда и т.д. Но постепенно сложился иной подход. Существенные закономерности оказалось можно обнаружить в области предельных величин. Предельные или пограничные величины характеризуют не состояние (как суммарная или средняя величины.), а процесс, изменение экономического объекта. Следовательно, производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

Можно сделать вывод, что производная – одно из самых важных понятий математического анализа. Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре, геометрии и других науках.

Министерство образования Саратовской области

Государственное автономное профессиональное образовательное учреждение Саратовской области «Энгельсский политехникум»

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В РАЗНИЧНЫХ ОБЛАСТЯХ НАУКИ

Выполнила: Саркулова Нургуля Сергеевна

студентка группы КШИ-216/15

(Конструирование, моделирование и

технология швейных изделий)

Научный руководитель:

Вербицкая Елена Вячеславовна

преподаватель математики ГАПОУ СО

«Энгельсский политехникум»

2016

Введение

Роль математики в различных областях естествознания очень велика. Недаром говорят «Математика – царица наук, физика ее правая рука, химия – левая».

Предмет исследования – производная.

Ведущая цель - показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.

Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

Ключевой и тематический вопросы данного реферата:

1. История возникновения производной.

2. Зачем изучать производные функций?

3. Где используются производные?

4. Применение производных в физике, химии, биологии и других науках.

5. Выводы

Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.

В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.

Применение производной в различных областях науки

Из курса алгебры старших классов мы уже знаем, что производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.

Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.

Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Физический смысл производной: производная функции y = f (x ) в точке x 0 – это скорость изменения функции f (x ) в точке x 0 .

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.

Геометрический смысл производной состоит в том, что производная функция в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .

Термин производная и современные обозначения y " , f " ввёл Ж.Лагранж в 1797г.

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.

Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.

Производная в алгебре:

1. Касательная к графику функции

Касательная к графику функции f, дифференцируемой в точке x о , - это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).

y = f (x о ) + f ′(x о ) (x – x о )

2. Поиск промежутков возрастания и убывания функции

Функция y=f(x) возрастает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X , если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

3. Поиск точек экстремума функции

Точку называют точкой максимума функции y=f(x) , если для всех x . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки понимают интервал , где - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

4. Поиск промежутков выпуклости и вогнутости функции

График функции , является на этом интервале выпуклым , лежит не выше любой своей касательной (рис. 1).

График функции , дифференцируемой на интервале , является на этом интервале вогнутым , если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2).

Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

5. Поиск точек изгиба функции

Производная в физике:

1. Скорость как производная пути

2. Ускорение как производная скорости a =

3. Скорость распада радиоактивных элементов 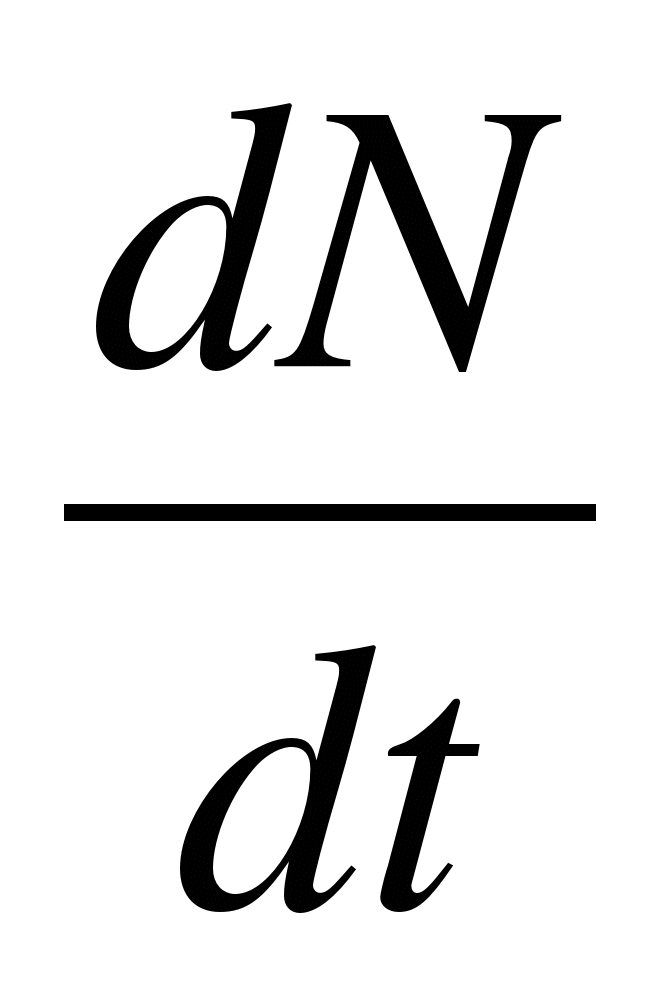= - λN

А так же в физике производную применяют для вычисления:

Скорости материальной точки

Мгновенной скорости как физический смысл производной

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

Производная в химии:

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Количество

в-ва в момент времени t 0

p = p(t 0 )

Функция

Интервал времени

∆t = t– t 0

Приращение аргумента

Изменение количества в-ва

∆p= p(t 0 + ∆ t) – p(t 0 )

Приращение функции

Средняя скорость химической реакции

∆p/∆t

Отношение приращёния функции к приращёнию аргумента

Производная в биологии:

Р = х‘ (t)

Производная в географии:

1. Некоторые значения в сейсмографии

2. Особенности электромагнитного поля земли

3. Радиоактивность ядерно- геоифзичексих показателей

4.Многие значения в экономической географии

5.Вывести формулу для вычисления численности населения на территории в момент времени t.

у’= к у

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует

Производная в электротехнике:

В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Производная в экономике:

Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.

Производная в экономике решает важные вопросы:

1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?

2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни

Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Список используемой литературы:

1. Богомолов Н.В., Самойленко И.И. Математика. - М.: Юрайт, 2015.

2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. - М.: Академия, 2014.

3. Баврин И.И. Основы высшей математики. - М.: Высшая школа, 2013.

4. Богомолов Н.В. Практические занятия по математике. - М.: Высшая школа, 2013.

5. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2013.

6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.

7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.: Издательский центр «Академия», 2010

8 . Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016

Периодические источники:

Газеты и журналы: «Математика», «Открытый урок»

Использование ресурсов сети Интернет, электронных библиотек:

www:egetutor.ru

matematika-na5.norod.ru

Задача. Функция издержек имеет вид , а доход при производстве х единиц товара определяется следующим образом:

Определить оптимальное для производителя значение выпуска х0.

Решение:

Прибыль Р(х) = D (x ) - С(х), где D (x ) - доход от производства х единиц продукта.

Функция прибыли имеет вид:

Найдем производную функции прибыли:

Очевидно, Р"(х)> 0 при х < 100, так что наибольшее значение прибыли на отрезке есть Р (100) = 399 900. Найдем теперь наибольшее значение прибыли на интервале (100; + ∞). Имеется одна критическая точка х= 200. При этом Р"(х) > 0 при 100 < x < 200 и Р " (х) < 0 при x > 200, т. е. х= 200- максимальное значение Р(х) на интервале (100; + ∞).

Р (200) = 419 900 > Р (100), таким образом, x опт = 200 (ед.).

Задача. Цементный завод производит Х т. цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т. цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т. в день.

Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:

К=-х3+98х2+200х . Удельные затраты составят К/х=-х2+98х+200

Решение:

Задача сводится к отысканию наибольшего и наименьшего значения функции

у= - х2+98х+200 . На промежутке .

DIV_ADBLOCK1021">

6 Применение производной в медицине

Применение дифференциального исчисления в медицине сводится к вычислению скорости. Например, скорости восстановительных реакций и скорости релаксационного процесса.

Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, изменении температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенного лекарства, его дозы. С помощью производной можно вычислить, при какой дозе лекарства реакция организма максимальна. С помощью второй производной можно определить условия, при которых скорость процесса наиболее чувствительна к каким-либо воздействиям

Задача Предположим, что х обозначает дозу назначенного лекарства, у - функция степени реакции. у=f(x)=x²(a-x), где а - некоторая положительная постоянная. При каком значении х реакция максимальна?

Решение:

https://pandia.ru/text/80/244/images/image137_6.gif" width="116" height="24">. Тогда при ..gif" width="49" height="42"> - тот уровень дозы, который дает максимальную реакцию.

Точки перегиба важны в биохимии , так как они определяют условия, при которых некоторая величина, например скорость процесса, наиболее (или наименее) чувствительна к каким-либо воздействиям.

Задача. В результате значительной потери крови содержание железа в крови уменьшилось на 210 мг. Недостаток железа вследствие его восстановления с течением времени t уменьшается по закону мг(t – сутки). Найти зависимость скорости восстановления железа в крови от времени. Вычислить эту скорость в момент t =0 и через 7 суток.

Решение:

Скорость восстановления железа:

https://pandia.ru/text/80/244/images/image144_5.gif" width="33" height="18"> скорость восстановления равна 30 мг/сутки. Через 7 суток скорость восстановления равна 11,1 мг/сут:

Релаксационный процесс – это процесс возвращения системы к состоянию устойчивого равновесия, из которого она была выведена. Во многих случаях (особенно при однократном воздействии) этот процесс описывается экспоненциальным уравнением https://pandia.ru/text/80/244/images/image147_6.gif" width="13" height="15 src="> – постоянная времени. Ее физический смысл: - это время, в течение которого начальное отклонение Научно-исследовательская деятельность" href="/text/category/nauchno_issledovatelmzskaya_deyatelmznostmz/" rel="bookmark">научно-производственной деятельности . Например, инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства , а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. В реальной жизни для решения производственных задач, в медицинской, сельскохозяйственной и химической промышленности важно знать скорости реакций химических веществ.

Пусть дана функция m=m(t), где m -количество некоторого вещества, вступившего в химическую реакцию в момент времени t . Приращению времени Δt будет соответствовать приращение Δm величины m . Отношение Δm/Δt - есть средняя скорость химической реакции за промежуток времени Δt . Предел этого отношения при стремлении Δt к нулю - есть скорость химической реакции в данный момент времени.

Задача. Зависимость между массой х вещества, получаемого в результате некоторой химической реакции и временем t выражается уравнением https://pandia.ru/text/80/244/images/image151_5.gif" width="283" height="30 src=">

Задача. Концентрация раствора изменяется с течением времени по закону: . Найти скорость растворения.

Решение:

Скорость растворение вычислим с помощью производной:

https://pandia.ru/text/80/244/images/image154_4.gif" width="139" height="42 src=">. Получите формулу для скорости роста численности популяции.

Решение:

Задача. Зависимость суточного удоя y в литрах от возраста коров х в годах определяется уравнением , где х>2 . Найдите возраст дойных коров, при котором суточный удой будет наибольшим.

Решение:

https://pandia.ru/text/80/244/images/image161_4.gif" width="77" height="23 src=">

(лет)- точка максимума, возраст дойных коров, при котором суточный удой будет наибольшим.

Заключение

В данной работе рассмотрено одно из важнейших понятий математического анализа - производная функции с точки зрения её практического применения. С помощью производной можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных возможно подробное исследование функций, более точное построение их графиков, решение уравнений и неравенств, доказательство тождеств и неравенств, нахождение наибольших и наименьших значений величин.

По всем вышеперечисленным областям применения производной подобрано и сведено в сборник около двухсот задач. Каждый раздел сборника начинается с краткого изложения теоретических основ, содержит типовые задачи с решениями и наборы упражнений для самостоятельного решения. Эти задачи расширяют кругозор и повышают интерес к производной. Они могут быть интересны и полезны студентам, увлекающимся математикой.

Литература

1. Богомолов задач по математике: учеб пособие для ссузов. – М.: Дрофа, 2005.

2. Богомолов: учеб. для ссузов / , – М.: Дрофа, 2010.

3. Богомолов. Дидактические задания: учеб. пособие для ссузов / , – М.: Дрофа, 2005.

4. Истомина: вопросы и ответы: учеб. пособие для вузов. – Ростов н/Д: Феникс, 2002.

5. Лисичкин: учеб. пособие для техникумов / , - М.:Высш. шк.,1991.

6. Никольский математического анализа: учеб. пособие для студ. ссузов.- М.: Дрофа, 2012.

7. Омельченко: учеб. пособие для ссузов. – Ростов н/Д: Феникс, 2007.

8. Филимонова: учеб. пособие для ссузов. – Ростов н/Д: Феникс, 2013.

ФГОУ СПО

Новосибирский аграрный колледж

Реферат

по дисциплине "математика"

"Применение производной в науке и технике"

С. Раздольное 2008 г.

Введение

1. Теоретическая часть

1.1 Задачи, приводящие к понятию производной

1.2 Определение производной

1.3 Общее правило нахождения производной

1.4 Геометрический смысл производной

1.5 Механический смысл производной

1.6 Производная второго порядка и её механический смысл

1.7 Определение и геометрический смысл дифференциала

2. Исследование функций с помощью производной

Заключение

Литература

Введение

В первой главе моего реферата речь пойдёт о понятии производной, правилах её применения, о геометрическом и физическом смысле производной. Во второй главе моего реферата речь пойдёт о применении производной в науке и технике и о решении задач в этой области.

1. Теоретическая часть

1.1 Задачи, приводящие к понятию производной

При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.

Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница.

Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).

Как известно, равномерным движением называют такое движение, при котором тело в равные промежутки времени проходит равные по длине отрезки пути. Путь, пройденный телом в единицу времени, называют скоростью равномерного движения.

Однако чаще всего на практике мы имеем дело с неравномерным движением. Автомобиль, едущий по дороге, замедляет движение у переходов и ускоряет его на тех участках, где путь свободен; самолёт снижает скорость при приземлении и т.д. Поэтому чаще всего нам приходится иметь дело с тем, что за равные отрезки времени тело проходит различные по длине отрезки пути. Такое движение называют неравномерным. Его скорость нельзя охарактеризовать одним числом.

Часто для характеристики неравномерного движения пользуются понятием средней скорости движения за время ∆t٫ которое определяется соотношением где ∆s – путь, пройденный телом за время ∆t.

Так, при свободном падении тела средняя скорость его движения за первые две секунды есть

Практически такая характеристика движения, как средняя скорость, говорит о движении очень мало. Действительно, при 4,9 м/с, а за 2-ю – 14,7 м/с, в то время как средняя скорость за первые две секунды составляет 9,8 м/с. Средняя скорость в течение первых двух секунд не даёт никакого представления о том, как происходило движение: когда тело двигалось быстрее, а когда медленнее. Если же задать средние скорости движения для каждой секунды в отдельности, то мы будем знать, например, что во 2-ю секунду тело двигалось значительно быстрее, чем в 1-ю. Однако в большинстве случаев значительно быстрее, чем нас мало устраивает. Ведь нетрудно понять, что в течение этой 2-й секунды тело также движется по-разному: в начале медленнее, в конце быстрее. А как оно движется где-то в середине этой 2-й секунды? Иными словами, как определить мгновенную скорость?

Пусть движение тела описывается законом Рассмотрим путь, пройденный телом за время от t 0 до t 0 + ∆t, т.е. за время, равное ∆t. В момент t 0 телом пройден путь , в момент – путь . Поэтому за время ∆t тело прошло путь и средняя скорость движения тела за этот промежуток времени составит.

Чем меньше промежуток времени ∆t, тем точнее можно установить, с какой скоростью движется тело в момент t 0 , так как движущееся тело не может значительно изменить скорость за малый промежуток времени. Поэтому средняя скорость при стремлении ∆t к нулю приближается к действительной скорости движения и в пределе даёт скорость движения в данный момент времени t 0 (мгновенную скорость).

Таким образом,

Определение 1. Мгновенная скорость прямолинейного движения тела в данный момент времени t 0 называется предел средней скорости за время от t 0 до t 0 + ∆t, когда промежуток времени ∆t стремится к нулю.

Итак, чтобы найти скорость прямолинейного неравномерного движения в данный момент, нужно найти предел отношения приращения пути ∆ к приращению времени ∆t при условии т.е. Лейбниц пришёл к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной своим уравнением.

Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к её траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на её орбите сводится, к определению направления касательной к кривой.

Определение касательной как прямой, имеющей с кривой только одну общую точку, справедливое для окружности, непригодно для многих других кривых.

Ниже представленное определение касательной к кривой, не только соответствует интуитивному представлению о ней, но и позволяет фактически находить её направление, т.е. вычислять угловой коэффициент касательной.

Определение 2. Касательной к кривой в точке М называется прямая МТ, которая является предельным положением секущей ММ 1 , когда точка М 1 , перемещаясь по кривой, неограниченно приближается к точке М.

1.2 Определение производной

Заметим, что при определении касательной к кривой и мгновенной скорости неравномерного движения, по существу, выполняются одни и те же математические операции:

1. Заданному значению аргумента дают приращение и вычисляют новое значение функции, соответствующее новому значению аргумента.

2. Определяют приращение функции, соответствующее выбранному приращению аргумента.

3. Приращение функции делят на приращение аргумента.

4. Вычисляют предел этого отношения при условии, что приращение аргумента стремится к нулю.

К предельным переходам такого типа приводят решения многих задач. Возникают необходимость сделать обобщение и дать название этому предельному переходу.

Скорость изменения функции в зависимости от изменения аргумента можно, очевидно, охарактеризовать отношением . Это отношение называется средней скоростью изменения функции на отрезке от до . Сейчас нужно рассмотреть предел дроби Предел этого отношения при стремлении приращения аргумента к нулю (если этот предел существует) представляет собой некоторую новую функцию от . Эту функцию обозначают символами y’, называют производной данной функции так как она получена (произведена) из функции Сама же функция называется первообразной функцией по отношению к своей производной

Определение 3. Производной функции в данной точке называют предел отношения приращения функции ∆y к соответствующему приращению аргумента ∆x при условии, что ∆x→0, т.е.

1.3 Общее правило нахождения производной

Операцию отыскания производной некоторой функции называют дифференцированием функции, а раздел математики, изучающий свойства этой операции, – дифференциальным исчислением.

Если функция имеет производную в точке x=a, то говорят, что она дифференцируема в этой точке. Если функция имеет производную в каждой точке данного промежутка, то говорят, что она дифференцируема на этом промежутке .

Определение производной не только с исчерпывающей полнотой характеризует понятие скорости изменения функции при изменении аргумента, но и даёт способ фактического вычисления производной данной функции. Для этого необходимо выполнить следующие четыре действия (четыре шага), указанные в самом определении производной:

1. Находят новое значение функции, представив в данную функцию вместо x новое значение аргумента : .

2. Определяют приращение функции, вычитывая данное значение функции из её нового значения: .

3. Составляют отношение приращения функции к приращению аргумента: .

4. Переходят к пределу при и находят производную: .

Вообще говоря, производная – это «новая» функция, произведённая от данной функции по указанному правилу.

1.4 Геометрический смысл производной

Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, состоит в следующем: значение производной функции в точке x равно угловому коэффициенту касательной, проведённой к графику функции в той же точке x, т.е.

Уравнение касательной, как всякой прямой, проходящей через данную точку в данном направлении, имеет вид – текущие координаты. Но и уравнение касательной запишется так: . Уравнение нормали запишется в виде .

1.5 Механический смысл производной

Механическое истолкование производной было впервые дано И. Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е. Таким образом, если закон движения материальной точки задан уравнением , то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени нужно найти производную и подставить в неё соответствующее значение t.

1.6 Производная второго порядка и её механический смысл

Получим (уравнение из проделанного в учебнике Лисичкин В.Т. Соловейчик И.Л. «математика» с. 240):

Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента. В этом и заключается механический смысл второй производной.

1.7 Определение и геометрический смысл дифференциала

Определение 4. Главная часть приращения функции, линейная относительно приращения функции, линейная относительно приращения независимой переменой, называется дифференциалом функции и обозначается знаком d, т.е. .

Дифференциал функции геометрически изображается приращением ординаты касательной, проведённой в точке M ( x ; y ) при данных значениях x и ∆x.

Вычисление дифференциала – .

Применение дифференциала в приближённых вычислениях – , приближённое значение приращения функции совпадает с её дифференциалом.

Теорема 1. Если дифференцируемая функция возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.

Теорема 2. Если производная функция положительна (отрицательна) в не котором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).

Сформулируем теперь правило нахождения интервалов монотонности функции

1. Вычисляют производную данной функции.

2. Находят точки, в которых равна нулю или не существует. Эти точки называются критическими для функции

3. Найденными точками область определения функции разбивается на интервалы, на каждом из которых производная сохраняет свой знак. Эти интервалы являются интервалами монотонности.

4. Исследуют знак на каждом из найденных интервалов. Если на рассматриваемом интервале , то на этом интервале возрастает; если же , то на таком интервале убывает.

В зависимости от условий задачи правило нахождения интервалов монотонности может упрощаться.

Определение 5. Точка называется точкой максимума (минимума) функции , если имеет место неравенство соответственно для любого x из не которой окрестности точки .

Если – точка максимума (минимума) функции , то говорят, что (минимум) в точке . Максимум и минимум функции объединяют название экстремум функции, а точки максимума и минимума называют точками экстремума (экстремальными точками).

Теорема 3. (необходимый признак экстремума). Если и производная в этой точке существует, то она равна нулю: .

Теорема 4. (достаточный признак экстремума). Если производная при переходе x через a меняет знак, то a является точкой экстремума функции .

Основные моменты исследования производной:

1. Находят производную .

2. Находят все критические точки из области определения функции.

3. Устанавливают знаки производной функции при переходе через критические точки и выписывают точки экстремума.

4. Вычисляют значения функции в каждой экстремальной точке.

2. Исследование функций с помощью производной

Задача №1 . Объём бревна. Круглым деловым лесом называют брёвна правильной формы без дефектов древесины с относительно небольшой разницей диаметров толстого и тонкого концов. При определении объёмов круглого делового леса обычно применяют упрощённую формулу , где – длина бревна, – площадь его среднего сечения. Выясните, завершается или занижается при этом реальный объём; оцените относительную погрешность.

Решение . Форма круглого делового леса близка к усечённому конусу. Пусть – радиус большего, меньшего конца бревна. Тогда его почти точный объём (объём усеченного конуса) можно, как известно, найти по формуле . Пусть – значение объёма, вычисленное по упрощённой формуле. Тогда ;

Т.е. . Значит, упрощённая формула даёт занижение величины объёма. Положим теперь . Тогда . Отсюда видно, что относительная погрешность не зависит от длины бревна, а определяется отношением . Поскольку при возрастает на промежутке . Поэтому , а значит, относительная погрешность не превосходит 3,7%. В практике лесоведения такая погрешность считается вполне допустимой. С большей точностью практически невозможно измерить ни диаметры торцов (ведь они несколько отличаются от кругов), ни длину бревна, поскольку измеряют не высоту, а образующую конуса (длина бревна в десятки раз больше диаметра, и это не приводит к большим погрешностям). Таким образом, на первый взгляд неправильная, но более простая формула для объёма усечённого конуса в реальной ситуации оказывается вполне правомерной. Многократно проводившиеся с помощью специальных методов проверки показали, что при массовом учёте делового леса относительная погрешность при использовании рассматриваемой формулы не превосходит 4%.

Задача №2 . При определении объёмов ям, траншей вёдер и других ёмкостей, имеющих форму усечённого конуса, в с/х практике иногда пользуются упрощённой формулой , где – высота, – площади оснований конуса. Выясните, завышается или занижается при этом реальный объём, оцените относительную погрешность при естественном для практики условии: ( – радиусы оснований, .

Решение . Обозначив через истинное значение объёма усечённого конуса, а через значение, вычисленное по упрощённой формуле, получим: , т.е. . Значит, упрощённая формула даёт завышение величины объёма. Повторив далее решение предыдущей задачи, найдём, что относительная погрешность будет не больше 6,7%. Вероятно, такая точность допустима при нормировании землеройных работ – ведь ямы не будут идеальными конусами, да и соответствующие параметры в реальных условиях замеряют весьма грубо.

Задача №3 . В специальной литературе для определения угла β поворота шпинделя фрезерного станка при фрезеровании муфт с зубьями выводится формула , где . Так как эта формула сложна, то рекомендуется отбросить её знаменатель и пользоваться упрощённой формулой . При каких ( – целое число, ) можно пользоваться этой формулой, если при определении угла допускается погрешность в ?

Решение. Точную формулу после несложных тождественных преобразований можно привести к виду . Поэтому при использовании приближённой формулы допускается абсолютная погрешность , где . Исследуем функцию на отрезке . При этом 0,06, т.е. угол принадлежит первой четверти. Имеем: . Заметим, что на рассматриваемом промежутке, а значит, функция на этом промежутке убывает. Поскольку далее , то при всех рассматриваемых . Значит, . Так как радиан, то достаточно решить неравенство . Решая это неравенство подбором, находим, что , . В силу того, что функция убывает, следует, что .

Заключение

Применение производной довольно широко, и его можно полностью охватить в работе такого типа, однако я попытался раскрыть основные базовые моменты. В наше время, в связь с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальными в решении как простых, так и сверхсложных задач.

Литература

1. В.А. Петров «Математический анализ в производственных задачках»

2. Соловейчик И.Л., Лисичкин В.Т. «Математика»

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Введение

Глава I

1.1 Исторические сведения

Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

Но это не говорит о том, …

Эпизодически понятие касательной встречалось в работах итальянского математика И. Тартальи (1499-1557).

Глава II. Применение физического смысла производной при решении физических задач

Применение производной в физике очень обширно. Рассмотрим несколько примеров применения производной в физических задачах.

1.1 Производная в механике

Механическое движение - это изменение положения тела в пространстве относительно других тел с течением времени.

Основной характеристикой механического движения служит скорость.

Алгоритм нахождения скорости тела с помощью производной.

Если закон движения тела задан уравнением s = s (t), то для нахождения мгновенной скорости тела в какой-нибудь определенный момент времени надо:

1. Найти производную s" = f " (t).

2. Подставить в полученную формулу заданное значение времени.

Да, т.к. скорость через 7 сек. будет равна 6м/с (21,6 км/ч).

1.2 Производная в электротехнике

В наших домах, на транспорте, на заводах: всюду работает электрический ток.

Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Задание.

Заряд, протекающий через проводник, меняется по закону

Найти силу тока в момент времени t=5 cек.

Сила тока равна 2 А

Сила есть производная работы по перемещению,

т.е. F=A / (x )

Теплоемкость - есть производная теплоты по температуре, т.е. C (t) = Q / (t)

d (l ) =m / (l ) - линейная плотность

K (t) = l / (t) - коэффициент линейного расширения

щ (t) = ц / (t) - угловая скорость

а (t) = щ / (t) - угловое ускорение

N (t) = A / (t) - мощность

Задание : теплота .

Решение . C (t) = Q / (t) = 0,396 + 4,162*10 - 3 t - 15,072*10 - 7 t 2

Глава III. Решение химических и биологических задач с помощью производной

3.1 Производная в химии

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Химия - это наука о веществах, о химических превращениях веществ.

Химия изучает закономерности протекания различных реакций.

Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.

Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Если C (t ) - закон изменения количества вещества, вступившего в химическую реакцию, то скорость v (t ) химической реакции в момент времени t равна производной:

3.2 Производная в биологии

Задача по биологии.

По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t.

Глава IV. Решение задач с географическим, экономическим содержанием

4.1 Производная в географии

Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Пусть у = у (t) - численность населения.

Рассмотрим прирост населения за t = t-t 0

y = k y t,

где к = к р - к с - коэффициент прироста (к р - коэффициент рождаемости,

к с - коэффициент смертности)

y: t=k y

При t0 получим lim y/ t=у"

у"= к у

4.2 Производная в экономике

Задание.

Оборот предприятия за истекший год описывается через функцию U (t) =0,15tі - 2tІ + 200, где t - месяцы, U-миллионы.

Исследуйте оборот предприятия за 9 и 10 месяцы.

Решение. Исследуем оборот предприятия с помощью производной: U" (t) =0,45tІ - 4t

Меньший оборот был на девятом месяце - 0,45. На 10 месяце - 5.

Заключение

Список используемых источников

Приложение

Подобные документы

Скачать:

Предварительный просмотр:

Подписи к слайдам:

Предварительный просмотр:

Подписи к слайдам:

Предварительный просмотр:

Подписи к слайдам:

Предварительный просмотр:

Подписи к слайдам:

Предварительный просмотр:

Решение . C (t) = Q / (t) = 0,396 + 4,16210 - 3 t - 15,07210 - 7 t 2