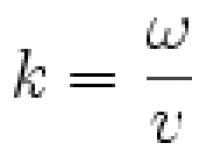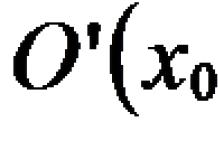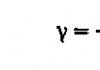Центростремительное ускорение - компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение , характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение ». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой .

Наиболее простым примером центростремительного ускорения является вектор ускорения при равномерном движении по окружности (направленный к центру окружности).

Осестремительное ускорение в проекции на плоскость, перпендикулярную оси, предстаёт как центростремительное.

Энциклопедичный YouTube

• 1 / 5

  A n = v 2 R {\displaystyle a_{n}={\frac {v^{2}}{R}}\ } a n = ω 2 R , {\displaystyle a_{n}=\omega ^{2}R\ ,}

  где a n {\displaystyle a_{n}\ } - нормальное (центростремительное) ускорение, v {\displaystyle v\ } - (мгновенная) линейная скорость движения по траектории, ω {\displaystyle \omega \ } - (мгновенная) угловая скорость этого движения относительно центра кривизны траектории, R {\displaystyle R\ } - радиус кривизны траектории в данной точке. (Связь между первой формулой и второй очевидна, учитывая v = ω R {\displaystyle v=\omega R\ } ).

  Выражения выше включают абсолютные величины. Их легко записать в векторном виде, домножив на e R {\displaystyle \mathbf {e} _{R}} - единичный вектор от центра кривизны траектории к данной её точке:

  a n = v 2 R e R = v 2 R 2 R {\displaystyle \mathbf {a} _{n}={\frac {v^{2}}{R}}\mathbf {e} _{R}={\frac {v^{2}}{R^{2}}}\mathbf {R} } a n = ω 2 R . {\displaystyle \mathbf {a} _{n}=\omega ^{2}\mathbf {R} .}

  Эти формулы равно применимы к случаю движения с постоянной (по абсолютной величине) скоростью, так и к произвольному случаю. Однако во втором надо иметь в виду, что центростремительное ускорение не есть полный вектор ускорения, а лишь его составляющая, перпендикулярная траектории (или, что то же, перпендикулярная вектору мгновенной скорости); в полный же вектор ускорения тогда входит еще и тангенциальная составляющая (тангенциальное ускорение ) a τ = d v / d t {\displaystyle a_{\tau }=dv/dt\ } , по направлению совпадающее с касательной к траектории (или, что то же, с мгновенной скоростью) .

  Мотивация и вывод

  То, что разложение вектора ускорения на компоненты - одну вдоль касательного к траектории вектора (тангенциальное ускорение) и другую ортогональную ему (нормальное ускорение) - может быть удобным и полезным, довольно очевидно само по себе. При движении с постоянной по модулю скоростью тангенциальная составляющая становится равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, как можно увидеть ниже, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Не говоря уже о важном частном случае движения по окружности.

  Формальный вывод

  Разложение ускорения на тангенциальную и нормальную компоненты (вторая из которых и есть центростремительное или нормальное ускорение) можно найти, продифференцировав по времени вектор скорости , представленный в виде v = v e τ {\displaystyle \mathbf {v} =v\,\mathbf {e} _{\tau }} через единичный вектор касательной e τ {\displaystyle \mathbf {e} _{\tau }} :

  a = d v d t = d (v e τ) d t = d v d t e τ + v d e τ d t = d v d t e τ + v d e τ d l d l d t = d v d t e τ + v 2 R e n , {\displaystyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d(v\mathbf {e} _{\tau })}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {e} _{\tau }+v{\frac {d\mathbf {e} _{\tau }}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {e} _{\tau }+v{\frac {d\mathbf {e} _{\tau }}{dl}}{\frac {dl}{dt}}={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {e} _{\tau }+{\frac {v^{2}}{R}}\mathbf {e} _{n}\ ,}

  Здесь использовано обозначение для единичного вектора нормали к траектории и l {\displaystyle l\ } - для текущей длины траектории ( l = l (t) {\displaystyle l=l(t)\ } ); в последнем переходе также использовано очевидное

  d l / d t = v {\displaystyle dl/dt=v\ }

  и, из геометрических соображений,

  d e τ d l = e n R . {\displaystyle {\frac {d\mathbf {e} _{\tau }}{dl}}={\frac {\mathbf {e} _{n}}{R}}.} v 2 R e n {\displaystyle {\frac {v^{2}}{R}}\mathbf {e} _{n}\ }

  Нормальным (центростремительным) ускорением. При этом его смысл, смысл входящих в него объектов, а также доказательство того факта, что он действительно ортогонален касательному вектору (то есть что e n {\displaystyle \mathbf {e} _{n}\ } - действительно вектор нормали) - будет следовать из геометрических соображений (впрочем, то, что производная любого вектора постоянной длины по времени перпендикулярна самому этому вектору, - достаточно простой факт; в данном случае мы применяем это утверждение для d e τ d t {\displaystyle {\frac {d\mathbf {e} _{\tau }}{dt}}}

  Замечания

  Легко заметить, что абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости.

  Приведенные здесь способы или их варианты могут быть использованы для введения таких понятий, как кривизна кривой и радиус кривизны кривой (поскольку в случае, когда кривая - окружность, R {\displaystyle R} совпадает с радиусом такой окружности; не слишком трудно также показать, что окружность в плоскости e τ , e n {\displaystyle \mathbf {e} _{\tau },\,e_{n}} с центром в направлении e n {\displaystyle e_{n}\ } от данной точки на расстоянии R {\displaystyle R} от неё - будет совпадать с данной кривой - траекторией - с точностью до второго порядка малости по расстоянию до данной точки).

  История

  Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс . Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач и т.д.

  Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).

  К XIX веку рассмотрение центростремительного ускорения становится уже совершенно рутинным как для чистой науки, так и для инженерных приложений.

  Позволяет нам существовать на этой планете. Как можно понять, что представляет собой центростремительное ускорение? Определение этой физической величины представлено ниже.

  Наблюдения

  Самый простой пример ускорения тела, движущегося по окружности, можно наблюдать, вращая камень на веревке. Вы тянете веревку, а веревка тянет камень к центру. В каждый момент времени веревка сообщает камню некоторое количество движения, и каждый раз - в новом направлении. Можно представить движение веревки в виде серии слабых рывков. Рывок - и веревка изменяет свое направление, еще рывок - еще раз изменение, и так по кругу. Если вы внезапно отпустите веревку, рывки прекратятся, а вместе с ними и прекратится изменение направления скорости. Камень будет двигаться в направлении касательной к кругу. Возникает вопрос: "С каким ускорением будет двигаться тело в это мгновение?"

  Формула центростремительного ускорения

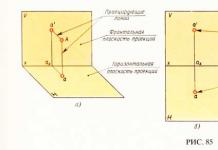
  Прежде всего стоит заметить, что движение тела по окружности является сложным. Камень участвует в двух видах движения одновременно: под действием силы он движется к центру вращения, и одновременно по касательной к окружности, от этого центра удаляется. Согласно Второму закону Ньютона, сила, удерживающая камень на веревке, направлена к центру вращения вдоль этой веревки. Туда же будет направлен вектор ускорения.

  Пусть за некоторое время t наш камень, равномерно двигаясь со скоростью V, попадает из точки A в точку B. Предположим, что в момент времени, когда тело пересекало точку B, на него перестала действовать центростремительная сила. Тогда за промежуток времени оно попало бы в точку K. Она лежит на касательной. Если бы в тот же момент времени на тело действовали бы только центростремительные силы, то за время t, двигаясь с одинаковым ускорением, оно оказалось бы в точке O, которая расположена на прямой, представляющей собой диаметр окружности. Оба отрезка являются векторами и подчиняются правилу векторного сложения. В результате суммирования этих двух движений за отрезок времени t получаем результирующую движения по дуге AB.

  

  Если промежуток времени t взять пренебрежимо малым, то дуга AB будет мало отличаться от хорды AB. Таким образом, можно заменить движение по дуге движением по хорде. В этом случае перемещение камня по хорде будет подчиняться законам прямолинейного движения, то есть пройденное расстояние AB будет равно произведению скорости камня на время его движения. AB = V х t.

  Обозначим искомое центростремительное ускорение буквой a. Тогда пройденный только под действием центростремительного ускорения путь можно рассчитать по формуле равноускоренного движения:

  Расстояние AB равно произведению скорости и времени, то есть AB = V х t,

  AO - вычислено ранее по формуле равноускоренного движения для перемещения по прямой: AO = at 2 / 2.

  Подставляя эти данные в формулу и преобразуя их, получаем простую и изящную формулу центростремительного ускорения:

  Словами это можно выразить так: центростремительное ускорение тела, двигающегося по окружности, равно частному от деления линейной скорости в квадрате на радиус окружности, по которой вращается тело. Центростремительная сила в таком случае будет выглядеть так, как на картинке ниже.

  

  Угловая скорость

  Угловая скорость равна частному от деления линейной скорости на радиус окружности. Верно и обратное утверждение: V = ωR, где ω - угловая скорость

  Если подставить это значение в формулу, можно получить выражение центробежного ускорения для угловой скорости. Оно будет выглядеть так:

  Ускорение без изменения скорости

  И все же, отчего тело с ускорением, направленным к центру, не движется быстрее и не перемещается ближе к центру вращения? Ответ кроется в самой формулировке ускорения. Факты говорят о том, что движение по окружности реально, но для его поддержания требуется ускорение, направленное к центру. Под действием силы, вызванной данным ускорением, происходит изменение количества движения, в результате чего траектория движения постоянно искривляется, все время меняя направление вектора скорости, но не изменяя ее абсолютной величины. Двигаясь по кругу, наш многострадальный камень устремляется внутрь, в противном случае он продолжал бы двигаться по касательной. Каждое мгновение времени, уходя по касательной, камень притягивается к центру, но не попадает в него. Еще одним примером центростремительного ускорения может стать водный лыжник, описывающий небольшие круги на воде. Фигура спортсмена наклонена; он как бы падает, продолжая движение и наклонившись вперед.

  

  Таким образом, можно сделать вывод о том, что ускорение не увеличивает скорость тела, так как векторы скорости и ускорения перпендикулярны друг к другу. Добавляясь к вектору скорости, ускорение лишь меняет направление движения и удерживает тело на орбите.

  Превышение запаса прочности

  В предыдущем опыте мы имели дело с идеальной веревкой, которая не рвалась. Но, допустим, наша веревка самая обычная, и даже можно вычислить усилие, после которого она просто порвется. Для того чтобы рассчитать эту силу, достаточно сопоставить запас прочности веревки с нагрузкой, которую она испытывает в процессе вращения камня. Вращая камень с большей скоростью, вы сообщаете ему большее количество движения, а значит, и большее ускорение.

  

  При диаметре джутовой веревки около 20 мм ее прочность на разрыв равна около 26 кН. Примечательно, что длина веревки нигде не фигурирует. Вращая груз размером в 1 кг на веревке радиусом в 1 м, можно вычислить, что линейная скорость, необходимая для ее разрыва равна 26 х 10 3 = 1кг х V 2 / 1 м. Таким образом, скорость, которую опасно превышать, будет равна √26 х 10 3 = 161 м/с.

  Сила тяжести

  При рассмотрении опыта мы пренебрегали действием силы тяжести, так как при таких больших скоростях ее влияние пренебрежимо мало. Но можно заметить, что при раскручивании длинной веревки тело описывает более сложную траекторию и постепенно приближается к земле.

  Небесные тела

  Если перенести законы движения по окружности в космос и применить их к движению небесных тел, можно заново открыть несколько давно знакомых формул. Например, сила, с которой тело притягивается к Земле, известна по формуле:

  В нашем случае множитель g и является тем самым центростремительным ускорением, которое было выведено из предыдущей формулы. Только в этом случае роль камня будет выполнять небесное тело, притягивающееся к Земле, а роль веревки - сила земного притяжения. Множитель g будет выражен через радиус нашей планеты и скорость ее вращения.

  

  Итоги

  Сущность центростремительного ускорения состоит в тяжелой и неблагодарной работе удержания движущегося тела на орбите. Наблюдается парадоксальный случай, когда при постоянном ускорении тело не изменяет величины своей скорости. Для неподготовленного ума такое заявление довольно парадоксально. Тем не менее и при расчете движения электрона вокруг ядра, и при вычислении скорости вращения звезды вокруг черной дыры, центростремительной ускорение играет не самую последнюю роль.

  Два луча, исходящие из нее, формируют угол. Его значение может быть определено как в радианах, так и в градусах. Теперь на некотором расстоянии от точки-центра мысленно проведем окружность. Мера угла, выраженная в радианах, в таком случае представляет собой математическое отношение длины дуги L, отделенной двумя лучами, к значению расстояния между центральной точкой и линией окружности (R), то есть:

  Если теперь представить описанную систему материальной, то к ней можно применить не только понятие угла и радиуса, но также центростремительное ускорение, вращение и т.д. Большинство из них описывают поведение точки, находящейся на вращающейся окружности. Кстати, сплошной диск также может быть представлен набором окружностей, различие которых лишь в расстоянии от центра.

  Одна из характеристик подобной вращающейся системы - это период обращения. Он указывает на значение времени, за которое точка на произвольной окружности возвратится к начальному положению или, что также верно, обернется на 360 градусов. При неизменной скорости вращения выполняется соответствие T = (2*3.1416) / Ug (здесь и далее Ug - угол).

  Частота вращения указывает на количество полных оборотов, выполняемых за 1 секунду. При неизменной скорости получаем v = 1 / T.

  Зависит от времени и так называемого угла поворота. То есть, если взять за начало отсчета произвольную точку А на окружности, то при вращении системы эта точка сместится до А1 за время t, образовав угол между радиусами А-центр и А1-центр. Зная время и угол, можно вычислить угловую скорость.

  А раз есть окружность, движение и скорость, значит, присутствует и центростремительное ускорение. Оно представляет собой одну из составляющих, описывающих перемещение в случае криволинейного движения. Термины «нормальное» и «центростремительное ускорение» идентичны. Отличие в том, что второй применяют для описания перемещения по кругу, когда вектор ускорения направлен к центру системы. Поэтому всегда необходимо знать, как именно двигается тело (точка) и его центростремительное ускорение. Определение его следующее: оно является быстротой изменения скорости, вектор которого направлен перпендикулярно направлению вектору и изменяет направленность последнего. В энциклопедии указано, что изучением данного вопроса занимался Гюйгенс. Формула центростремительного ускорения, предложенная им, выглядит как:

  Acs = (v*v) / r,

  где r - радиус кривизны пройденного пути; v - скорость перемещения.

  Формула, по которой рассчитывают центростремительное ускорение, до сих пор вызывает жаркие споры среди энтузиастов. К примеру, недавно была озвучена любопытная теория.

  Гюйгенс, рассматривая систему, исходил из того, что тело перемещается по кругу радиуса R со скоростью v, замеренной в начальной точке А. Так как вектор инерции направлен по то получается траектория в виде прямой АБ. Однако центростремительная сила удерживает тело на кругу в точке С. Если обозначить центр за О и провести линии АБ, БО (сумма БС и СО), а также АО, то получается треугольник. В соответствии с законом Пифагора:

  БС=(a*(t*t)) / 2, где а - ускорение; t - время (a*t*t - это и есть скорость).

  Если теперь использовать формулу Пифагора, то:

  R2+t2+v2 = R2+(a*t2*2*R) / 2+ (a*t2/2)2, где R - радиус, а буквено-цифровое написание без знака умножения - степень.

  Гюйгенс допустил, что, так как время t мало, то его можно в расчетах не учитывать. Преобразовав предыдущую формулу, она пришел к известной Acs = (v*v) / r.

  Однако так как время взято в квадрате, то возникает прогрессия: чем больше t, тем выше погрешность. Например, для 0.9 оказывается неучтенными почти итогового значения 20%.

  Понятие центростремительного ускорения важно для современной науки, но, очевидно, что в этом вопросе еще рано ставить точку.

  Пусть материальная точка равномерно движется по окружности. Тогда модуль ее скорости не изменяется ($v=const$). Но это не значит, что ускорение материальной точки равно нулю. Вектор скорости направлен по касательной к траектории движения точки. При перемещении по окружности скорость изменяет свое направление постоянно. Значит, точка движется с ускорением.

  Рассмотрим точки A и B принадлежащие траектории движения рассматриваемого тела. Вектор изменения скорости для этих точек равен:

  \[\Delta \overline{v}={\overline{v}}"-\overline{v}\left(1\right).\]

  Если время движения, между точками A и B мало, то дуга AB мало отличается от хорды AB. Треугольники AOB и BMN подобны, следовательно:

  \[\frac{\Delta v}{v}=\frac{\Delta l}{r}=\alpha \left(2\right).\]

  Модуль среднего ускорения найдем как:

  \[\left\langle a\right\rangle =\frac{\Delta v}{\Delta t}=\frac{v\Delta l}{r\Delta t}\left(3\right).\]

  Величину мгновенного ускорения можно получить, перейдя к пределу при $\Delta t\to 0\ $ от $\left\langle a\right\rangle $:

  Вектор среднего ускорения составляет с вектором скорости угол равный:

  \[\beta =\frac{\pi +\alpha }{2}\left(5\right).\]

  При $\Delta t\to 0\ $ угол $\alpha \to 0.$ Получается, что вектор мгновенного ускорения составляет с вектором скорости угол $\frac{\pi }{2}$.

  Мы получили, что материальная точка, равномерно движущаяся по окружности, имеет ускорение, направленное к центру траектории движения (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности. Такое ускорение называют центростремительным или нормальным , обозначают его обычно ${\overline{a}}_n$.

  где $\omega $ - угловая скорость движения материальной точки ($v=\omega \cdot r$).

  Определение центростремительного ускорения

  Определение

  И так, центростремительное ускорение (в общем случае) - это составляющая полного ускорения материальной точки, которая характеризует, как быстро изменяется направление вектора скорости при криволинейном перемещении. Другой компонентой полного ускорения является тангенциальное ускорение, оно отвечает за изменение величины скорости.

  Центростремительное ускорение равно:

  \[{\overline{a}}_n=\frac{v^2}{r^2}\overline{r\ }\left(7\right),\]

  где $e_r=\frac{\overline{r\ }}{r}$ - единичный вектор, направленный от центра кривизны траектории к рассматриваемой точке.

  Впервые верные формулы для центростремительного ускорения были получены Х. Гюйгенсом.

  Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:

  \[\left=\frac{м}{с^2}.\]

  Примеры задач с решением

  Пример 1

  Задание. Диск вращается вокруг неподвижной оси. Закон изменения угла поворота радиуса диска задает уравнение: $\varphi =5t^2+7\ (рад)$. Чему равно центростремительное ускорение точки A диска, которая находится на расстоянии $r=$0,5 м от оси вращения к окончанию четвертой секунды от начала вращения?

  Решение. Сделаем рисунок.

  

  Модуль центростремительного ускорения равен: \

  Угловую скорость вращения точки найдем как:

  \[\omega =\frac{d\varphi }{dt}\ (1.2)\]

  уравнение изменения угла поворота в зависимости о времени:

  \[\omega =\frac{d\left(5t^2+7\right)}{dt}=10t\ \left(1.3\right).\]

  В конце четвертой секунды угловая скорость равна:

  \[\omega \left(t=4\right)=10\cdot 4=40\ \left(\frac{рад}{с}\right).\]

  Используя выражение (1.1) найдем величину центростремительного ускорения:

  Ответ. $a_n=800\frac{м}{с^2}$.

  Пример 2

  Задание. Движение материальной точки задается при помощи уравнения: $\overline{r}\left(t\right)=0,5\ (\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin (\omega t)\ }\ })$, где $\omega =2\ \frac{рад}{с}$. Какова величина нормального ускорения точки?

  Решение. За основу решения задачи примем определение центростремительного ускорения в виде:

  Из условий задачи видно, что траекторией движения точки является окружность. В параметрическом виде уравнение: $\overline{r}\left(t\right)=0,5\ (\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin (\omega t)\ }\ })$, где $\omega =2\ \frac{рад}{с}$ можно представить как:

  \[\left\{ \begin{array}{c} x=0,5{\cos \left(2t\right);;\ } \\ y=0,5{\sin \left(2t\right).\ } \end{array} \right.\]

  Радиус траектории можно найти как:

  Компоненты скорости равны:

  \ \

  Получим модуль скорости:

  Подставим величину скорости и радиус окружности в выражение (2.2), имеем:

  Ответ. $a_n=2\frac{м}{с^2}$.