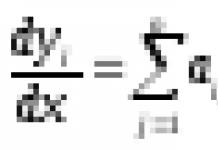Кроме рассмотренного выше аналитического метода определения перемещения балки, существуют другие аналитические и графоаналитические методы, применимые для более сложных систем, например, конструкций с ломаной осью и статически неопределимых систем.

Один из таких методов основан на интеграле Мора и правиле Верещагина. Сущность метода заключается в приложении в направлении интересующего нас перемещения единичной нагрузки (силы или момента силы) и вычислении интеграла Мора. Выражение для интеграла Мора выводится на основе теоремы Кастильяно, которая формулируется здесь без доказательства.

Теорема Кастильяно. Производная потенциальной энергии деформации по обобщенной силе рана обобщенному перемещению.

Потенциальная энергия деформации изогнутой балки выражается формулой

На основании теоремы Кастильяно обобщенное (линейное или угловое) перемещение Д определяется, как

Если обобщенную силу Q 06 приравнять к единице, то частная производная будет численно равна моменту М° единичной нагрузки

в сечении г балки (частные производные моментов других сил равны нулю, так как эти моменты от единичной нагрузки не зависят). В результате получается формула, называемая интегралом Мора.

Для отдельного участка конструкции интеграл Мора записывается в виде

где Д - обобщенное (линейное или угловое) перемещение; / - длина участка; М - уравнение моментов внешних сил; М° - уравнение моментов единичной нагрузки; ?7 - жесткость участка конструкции.

Для определения линейного перемещения к участку прикладывается единичная безразмерная сила, а для определения углового перемещения - единичный безразмерный момент. Для конструкции с постоянной жесткостью ее можно вынести за знак интеграла, тогда

В качестве примера вычислим интеграл Мора для балки, показанной на рис. 6.27

Рис. 6.27

Так как функции изгибающих моментов графически выражаются эпюрами моментов, то представляется возможным выразить интеграл Мора через площади и ординаты эпюр по правилу Верещагина , иначе называемому методом перемножения эпюр. Это правило формулируется так: искомый интеграл равен произведению площади грузовой эпюры М на расположенную под ее центром тяжести ординату единичной эпюры. Грузовой названа эпюра изгибающих моментов внешних сил.

Площади и ординаты эпюр берутся со знаками плюс или минус, а положительный результат означает, что направление искомого перемещения совпадает с направлением единичной нагрузки. Если рассматриваемая конструкция имеет несколько участков, то расчеты проводятся для каждого участка в отдельности, а результат суммируется.

В качестве примера определим по правилу Верещагина линейное перемещение и угол поворота концевого сечения балки, изображенной на рис. 6.24.

Для определения линейного перемещения свободного конца балки приложим к ее концу вертикальную единичную силу и рассмотрим грузовую эпюру и эпюру моментов единичной силы. Тогда

что совпадает с выражением для у в, полученным в Примере 6.8.

Для определения угла поворота концевого сечения балки приложим к ее концу единичный момент и построим эпюру. Тогда

Положительные ответы означают, что направления единичных нагрузок и перемещений совпадают. Тот же результат мы получим, если перемножим площадь единичной эпюры на ординату грузовой эпюры, расположенную над центром тяжести площади единичной эпюры.

Для раскрытия статической неопределимости системы следует отбросить одну из опор, заменить ее реакциями, приложить единичную нагрузку, а затем построить грузовую и единичную эпюры. Перемножив эпюры по правилу Верещагина и приравняв полученное перемещение к нулю, получим дополнительное уравнение, необходимое для раскрытия статической неопределимости системы.

Пример 6.11

Раскрыть статическую неопределимость двухопорной рамы квадратной формы со стороной /, показанной на рис. 6.28, а.

Решение. Отбросим опоры, заменив их реакциями Х ь Y u Х 2 , Y 2 . Составив уравнение моментов относительно опор и решая их, получим Y 2 -P , Y x = -Р . Уравнение проекции на горизонтальную ось Р-Х х +Х 2 = 0 имеет два неизвестных. Приложим к правому концу рамы единичную силу, как показано на рис. 6.28, д и построим эпюру единичных моментов. На рис. 6.28, виг построены грузовые эпюры изгибающих моментов. Перемножив по правилу

Рис. 6.28

Верещагина грузовые и единичную эпюры, получим дополнительное уравнение, необходимое для раскрытия статической неопределимости рамы.

Знак минус в третьем слагаемом возникает потому, что эпюры активной силы Р и единичной силы расположены по разные стороны от оси стержня.

Произведя вычисления, получим , откуда. Минус в ответе означает то, что реакция Х 2 направлена в противоположную сторону. Далее находим

Определение перемещений. Метод О. Мора в сочетании со способом (формулой) Симпсона

Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение , и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила , а если требуется найти угол поворота , то приложить следует сосредоточенную пару.

Далее в одном и том же произвольном сечении обоих состояний (то есть и действительного, и вспомогательного) составляются аналитические выражения изгибающего момента, которые подставляются в формулу, называемую «интегралом Мора»:

где: знак Σ распространяется на все участки балки,

а EI – изгибная жесткость на участке.

Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр . Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:

Здесь обозначено: a , b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М ,

– крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния.

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака ), то перед их произведением мы должны поставить знак «плюс : а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Следует иметь в виду, что способы «перемножения» эпюр (кроме способа Симпсона известен еще способ Верещагина ) применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI = Const ),
2. Одна из двух эпюр моментов на этом участке должна быть обязательно линейной . При этом обе эпюры не должны в пределах данного участка иметь перелома.

При наличии нескольких участков на балке, удовлетворяющих указанным двум условиям, формула для определения перемещений принимает вид:

Если результат вычисления получается положительным , то, следовательно, направление искомого перемещения совпадает с направлением «единичного силового фактора» (), а если результат отрицательный, значит искомое перемещение происходит в направлении, противоположном этому фактору.

Формула Симпсона, записанная через моменты , выглядит следующим образом: перемещения (прогиб или угол поворота) равны

где li – длина участка ;

EIi – жесткость балки на участке;

M F – значения изгибающих моментов с грузовой эпюры , соответственно участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

При перемножении эпюр будет полезным для определения ординат эпюр изгибающих моментов:

, где

Задача

Определить угол поворота сечения на левой опоре φ А

1) Находим опорные реакции действительного состояния .

2) Строим эпюру моментов действительного состояния М .

3) Выбираем вспомогательное состояние для определения угла поворота φ А.

4) Находим опорные реакции вспомогательного состояния

«Реагируем» на знак «минус».

5) Строим эпюру моментов вспомогательного состояния :

6) «Перемножаем» эпюры

Поскольку одна из них (а именно) линейна на всем пролете и не имеет перелома, а эпюра М тоже без перелома, то в формуле Симпсона будет всего один участок, и тогда

Знак «плюс» говорит о том, что сечение А поворачивается в сторону «единичного момента»

prosopromat.ru

Формула Симпсона для определения перемещений

Для определения перемещения по формуле Симпсона необходимо:

1. Построить грузовую эпюру моментов (эпюру моментов от действия всех внешних нагрузок).
2. Построить единичную эпюру моментов. Для этого в сечении, где нужно определить линейное перемещение (прогиб) приложить единичную силу, а для определения углового перемещения - единичный момент, и от данного единичного фактора построить эпюру изгибающих моментов.
3. Перемножить эпюры (грузовую и единичную) по формуле, которая называется формулой Симпсона:

где l i – длина участка ;

EI i – жесткость балки на участке ;

грузовой эпюры, соответственно

– значения изгибающих моментов с единичной эпюры, соответственно

Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».

prosopromat.ru

2.8 Основные варианты перемножения эпюр

Очевидно, что разнообразие приложенных
нагрузок и геометрических схем
конструкций приводит к различным, с
точки зрения геометрии, перемножаемым
эпюрам. Для реализации правила Верещагина
нужно знать площади геометрических
фигур и координаты их центров тяжести.
На рис.29 представлены некоторые основные
варианты, возникающие в практических
расчетах.

Для перемножения эпюр сложной формы
их необходимо разбивать на простейшие.
Например, для перемножения двух эпюр,
имеющих вид трапеции, нужно одну из них
разбить на треугольник и прямоугольник,
умножить площадь каждого из них на
ординату второй эпюры, расположенную
под соответствующим центром тяжести,
и результаты сложить. Аналогично
поступают и для умножения криволинейной
трапеции на любую линейную эпюру.

Если указанные выше действия проделать
в общем виде, то получим для таких
сложных случаев формулы, удобные для
использования в практических расчетах
(рис.30). Так, результат перемножения
двух трапеций (рис.30,а):

Рис. 29

По формуле (2.21) можно перемножить и
эпюры, имеющих вид “перекрученных”
трапеций (рис.30,б), но при этом произведение
ординат, расположенных по разные стороны
от осей эпюр, учитывается со знаком
минус.

Если одна из перемножаемых эпюр очерчена
по квадратной параболе (что соответствует
нагружению равномерно распределенной
нагрузкой), то для перемножения со
второй (обязательно линейной) эпюрой
ее рассматривают как сумму (рис.30,в) или
разность (рис.30,г) трапециидальной и
параболической эпюр. Результат
перемножения в обоих случаях определяется
формулой:

но значение f при этом определяется
по-разному (рис. 30, в, г).

Рис. 30

Возможны случаи, когда ни одна из
перемножаемых эпюр не является
прямолинейной, но хотя бы одна из них
ограничена ломаными прямыми линиями.
Для перемножения таких эпюр их
предварительно разбивают на участки,
в пределах каждого из которых по крайней
мере одна эпюра являетя прямолинейной.

Рассмотрим использование правила
Верещагина на конкретных примерах.

Пример 15. Определить прогиб в
середине пролета и угол поворота левого
опорного сечения балки, нагруженной
равномерно распределенной нагрузкой
(рис.31,а), способом Верещагина.

Последовательность расчета способом
Верещагина – такая же, как и в методе
Мора, поэтому рассмотрим три состояния
балки: грузовое – при действии
распределенной нагрузки q; ему
соответствует эпюра M q (рис.31,б),
и два единичных состояния – при действии
силы
приложенной в точке С (эпюра
,
рис.31,в), и момента
,
приложенного в точке В (эпюра
,
рис.31,г).

Прогиб балки в середине пролета:

Аналогичный результат был получен
ранее методом Мора (см. пример 13). Следует
обратить внимание на тот факт, что
перемножение эпюр выполнялось для
половины балки, а затем, в силу симметрии,
результат удваивался. Если же площадь
всей эпюры M q умножить на
расположенную под ее центром тяжести
ординату эпюры
(
на
рис.31,в), то величина перемещения будет
совершенно иной и неправильной так как
эпюра
ограничена ломаной линией. На
недопустимость такого подхода уже
указывалось выше.

А при вычислении угла поворота сечения
в точке В можно площадь эпюры M q умножить на расположенную под ее центром
тяжести ординату эпюры
(
,
рис.31,г), так как эпюра
ограничена прямой линией:

Этот результат также совпадает с
результатом, полученным ранее методом
Мора (см. пример 13).

Рис. 31

Пример 16. Определить горизонтальное
и вертикальное перемещения точки А в
раме (рис.32,а).

Как и в предыдущем примере, для решения
задачи необходимо рассмотреть три
состояния рамы: грузовое и два единичных.
Эпюра моментов M F , соответствующая
первому состоянию, представлена на
рис.32,б. Для вычисления горизонтального
перемещения прикладываем в точке А по
направлению искомого перемещения (т.е.
горизонтально) силу
,
а для вычисления вертикального
перемещения силу
прикладываем вертикально (рис.32,в,д).
Соответствующие эпюры
и
показаны на рис.32,г,е.

Горизонтальное перемещение точки А:

При вычислении

на участке АВ трапеция (эпюра M F)
разбита на треугольник и прямоугольник,
после чего треугольник с эпюры
“умножен”
на каждую из этих фигур. На участке ВС
криволинейная трапеция разделена на
криволинейный треугольник и прямоугольник,
а для перемножения эпюр на участке СД
использована формула (2.21).

Знак ” – “, полученный при вычислении

,
означает, что точка А перемещается по
горизонтали не влево (в этом направлении
приложена сила
),
а вправо.

Здесь знак ” – ” означает, что точка
А перемещается вниз, а не вверх.

Отметим, что единичные эпюры моментов,
построенные от силы

,
имеют размерность длины, а единичные
эпюры моментов построенные от момента
,
являются безразмерными.

Пример 17. Определить вертикальное
перемещение точки А плоско-пространственной
системы (рис.33,а).

Рис.23

Как известно (см. гл.1), в поперечных
сечениях стержней плоско-пространственной
системы возникают три внутренних
силовых фактора: поперечная сила Q y ,
изгибающий момент M x и крутящий
момент M кр. Так как влияние
поперечной силы на величину перемещения
незначительно (см. пример 14,
рис.27), то при вычислении перемещения
методом Мора и Верещагина из шести
слагаемых остаются только два.

Для решения задачи построим эпюры
изгибающих моментов M x,q и крутящих
моментов М кр,q от внешней нагрузки
(рис.33,б), а затем в точке А приложим силу
по направлению искомого перемещения,
т.е. вертикального (рис.33,в), и построим
единичные эпюры изгибающих моментов
и крутящих моментов
(рис.33,г).
Стрелками на эпюрах крутящих моментов
показаны направления закручивания
соответствующих участков
плоско-пространственной системы.

Вертикальное перемещение точки А:

При перемножении эпюр крутящих моментов
произведение берется со знаком “+”,
если стрелки, указывающие направление
кручения, сонаправленны, и со знаком ”
– ” – в противном случае.

studfiles.net

Перемножение эпюр способом Верещагина

Для вы­числения необходимо провести сле­дующие операции:

1. Построить эпюры изгибающих моментов Мр и Мк соответственно от заданного и единичного нагружений балки. При сложном нагружении балки (фиг. 19, а) следует: либо эпюру Мр разбить на простейшие части, для которых величина площади и по­ложение центра тяжести известны (фиг. 19, б), либо (предпочтительно) построить эпюру Мр в расслоенном виде (фиг. 19, в).

Если балка ступенчато переменного сечения, эпюра Мр должна быть, кроме того, разбита на участки, в пре­делах которых жесткость сечения по­стоянна.

2. На каждом участке помножить площадь ω одной из эпюр (например, эпюры Мр) на ординату Мс другой эпюры (например, эпюры Мк) под центром тяжести первой эпюры и по­лученное произведение разделить на коэффициент ступенчатости j.

При этом ордината Мс должна быть взята на эпюре, которая на рассматриваемом участке меняется по линейному закону (без излома). Если же эпюра является лома­ной, ее следует разбить на участки, в пределах которых она окажется линейной.

3. Вычислить сумму слагаемых, ука­занных в п. 2.

Формула для определения переме­щения по рассматриваемому способу

где суммирование производят по всем участкам балки

Площади и координаты центров тя­жести некоторых эпюр даны в табл. 11. Результаты перемножения часто встре­чающихся грузовых и единичных эпюр приведены в табл. 12.

Пример. Определить угол поворота се­ чения В ступенчатой балки (см.фиг. 19, а).

Определив опорные реакций Аи В, построим эпюру Мр на фиг. 19, б и в изо­бражены нерасслоенная и расслоенная эпю­ры Мр. Приложив к точке В освобожденной от нагрузки балки единичный момент, по­строим единичную эпюру М1 (фиг, 19. г).

Используя расслоенную эпюру Мр,по формуле 36 и табл. 12 определяем искомый угол поворота сечения В:

Фиг. 20

Пример. Определить прогиб в точке К балки постоянного поперечного сечения (фиг. 20, а).

Приложив к точке К,освобожденной от заданной нагрузки балки, единичную силу, построим единичную эпюру изгибающих мо­ментов Мк (фиг. 20, б).
Определив опорные реакции от заданной нагрузки

отрежем консоль и заменим ее силой qa и моментом (фиг. 20, в).

Построим, эпюру М расслоенной (от каждого вида нагрузки в отдельности), под­ходя к месту излома единичной эпюры Мк с двух сторон (фиг. 20, i ).

По формуле (36) с использованием табл. 12 определяем искомое перемещение

Заказать решение Способ оплаты

funnystudy.ru

Определение перемещений в балке по формуле Симпсона

Для балки определить линейные и угловые перемещения в точках A, B, C, предварительно подобрав сечение двутавра из условия прочности.

Дано: a =2 м, b =4 м, с=3 м, F =20 кН, М=18 кН м, q =6 кН/м, σ adm =160 МПа, Е=2 10 5 МПа

1) Вычерчиваем схему балки, определяем опорные реакции. В жёсткой заделке возникает 3 реакции - вертикальная и горизонтальная , а так же опорный момент. Поскольку горизонтальных нагрузок нет – соответствующая реакция равна нулю. Для того, чтобы найти реакции в точке E, составим уравнения равновесия.

∑F y = 0 q7-F+R E =0

R E =-q7+F=-67+20=-22кН (знак говорит о том, что

Найдем опорный момент в жесткой заделке , для чего решим уравнение моментов относительно любой выбранной точки.

∑M C: -M E -R E 9-F6-q77/2-M=0

M E =-18-229+649/2=-18-198+147=-69кНм (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)

2) Строим грузовую эпюру M F – эпюру моментов от заданной нагрузки.

Для построения эпюр моментов найдем моменты в характерных точках . В точке В определяем моменты как от правых, так и от левых сил , поскольку в этой точке приложен момент.

Для построения эпюры момента на линии действия распределенной нагрузки (участки АВ и ВС ) нам нужны дополнительные точки для построения кривой. Определим моменты в серединах этих участков. Это моменты в серединах участков АВ и ВС 15,34 кНм и 23,25кНм . Строим грузовую эпюру.

3) Для определения линейных и угловых перемещений в точке необходимо приложить в этой точке, в первом случае, единичную силу (F=1) и построить эпюру моментов, во втором случае, единичный момент (M=1 ) и построить эпюру моментов. Строим эпюры от единичных нагрузок для каждой точки – А, В и С.

4) Для нахождения перемещений мы используем формулу Симпсона.

где l i – длина участка;

EI i – жесткость балки на участке;

M F – значения изгибающих моментов с грузовой эпюры , соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры , соответственно в начале, в середине и в конце участка.

Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».

Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.

Рассмотрим применение формулы Симпсона на примере определения перемещений в точке А.

Определим прогиб, перемножив грузовую эпюру на эпюру от единичной силы.

Прогиб получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением единичной силы (направлено вверх).

Определим угол поворота , перемножив грузовую эпюру на эпюру от единичного момента.

Угол поворота получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного момента (направлен против часовой стрелки).

5) Для определения конкретных значений перемещений требуется подобрать сечение. Подберем сечение двутавра

где M max – это максимальный момент на грузовой эпюре моментов

Подбираем по сортаменту двутавр №30 с W x =472см 3 и I x = 7080см 4

6) Определяем перемещения в точках, раскрывая жесткость сечения: E – модуль продольной упругости материала или модуль Юнга (2 10 5 МПа), J x – осевой момент инерции сечения

Прогиб в точке А (вверх)

Угол поворота (против часовой стрелки)

Если требуется построить изогнутую ось балки , то балка вычерчивается без нагрузки, и в точках откладываются прогибы в соответствующие стороны - строится плавная кривая – изогнутая ось балки.

prosopromat.ru

Перемножение эпюр по правилу, методу или способу Мора-Верещагина

Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем, это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.

Что нужно знать для успешного освоения материалов данного урока?

Обязательно нужно знать, как строится эпюра изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.

Верещагин и его метод, правило или способ

А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:​

\({ V={ M }_{ F } }\cdot \overline { M } ={ \omega }_{ C }\cdot { \overline { M } }_{ C } \)​

Проиллюстрировано перемножение эпюр по Верещагину: C - центр тяжести первой эпюры, ωс - площадь первой эпюры, Mc - ордината второй эпюры под центром тяжести первой.

Площадь и центр тяжести эпюр

При использовании метода Верещагина, берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.

Любую эпюру можно расслоить всего на три фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.

Перемножение эпюр по Верещагину

В этом блоке статьи покажу частные случаи перемножения эпюр по Верещагину.

Прямоугольник на прямоугольник

​\({ V={ M }_{ F } }\cdot \overline { M } ={ b\cdot h\cdot c } \)​

Прямоугольник на треугольник

​\({ V={ M }_{ F } }\cdot \overline { M } ={ b\cdot h\cdot \frac { 1 }{ 2 } \cdot c } \)​

Треугольник на прямоугольник

​\({ V={ M }_{ F } }\cdot \overline { M } ={ \frac { 1 }{ 2 } \cdot b\cdot h\cdot c } \)​

Сегмент на прямоугольник

​\({ V={ M }_{ F } }\cdot \overline { M } ={ \frac { q\cdot { l }^{ 3 } }{ 12 } \cdot c } \)​

Сегмент на треугольник

​\({ V={ M }_{ F } }\cdot \overline { M } ={ \frac { q\cdot { l }^{ 3 } }{ 12 } \cdot \frac { 1 }{ 2 } \cdot c } \)​

Частные случаи расслоения эпюр на простые фигуры

В этом блоке статьи покажу частные случаи расслоения эпюр на простые фигуры, для возможности их перемножения по Верещагину.

Прямоугольник и треугольник

Два треугольника

Два треугольника и сегмент

Треугольник, прямоугольник и сегмент

Пример определения перемещений: прогибов и углов поворотов по Верещагину

Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.

Построение эпюры изгибающих моментов

В первую очередь, рассчитываем и строим эпюру изгибающих моментов:

Построение единичных эпюр моментов

Теперь для каждого искомого перемещений необходимо приложить единичную нагрузку (безразмерную величину равную единице) и построить единичные эпюры:

• Для прогибов, прикладываются единичные силы.
• Для углов поворотов, прикладываются единичные моменты.

Причем направление этих нагрузок не важно! Расчет покажет верное направление перемещений.

Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой силы. Тоже самое касается и углов поворотов.

Перемножение участков эпюры по Верещагину

После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.

Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов , в этом уроке будем придерживаться этого же правила.

Определение прогиба сечения С

Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора - Верещагина:

\[ { V }_{ C }=\frac { 1 }{ E{ I }_{ x } } (\frac { 1 }{ 2 } \cdot 6\cdot 3\cdot \frac { 2 }{ 3 } \cdot 2+\frac { 1 }{ 2 } \cdot 6\cdot 2\cdot \frac { 2 }{ 3 } \cdot 2)=\frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } \]

Представим, что рассчитываемая балки имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:

\[ { V }_{ C }=\frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } =\frac { 20\cdot { 10 }^{ 9 }Н\cdot { см }^{ 3 } }{ 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 3460{ см }^{ 4 } } =0.289см \]

Определение угла поворота сечения С

Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора - Верещагина:

\[ { \theta }_{ C }=\frac { 1 }{ E{ I }_{ x } } (-\frac { 1 }{ 2 } \cdot 6\cdot 3\cdot \frac { 1 }{ 3 } \cdot 1)=-\frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } \]

\[ { { \theta } }_{ C }=-\frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } =-\frac { 3\cdot { 10 }^{ 7 }Н\cdot { см }^{ 3 } }{ 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 3460{ см }^{ 4 } } =-0.0004рад \]

sopromats.ru

Формулы трапеций и Симпсона

Воспользуемся
правилом Верещагина для перемножения
двух прямолинейных эпюр, имеющих вид
трапеций. Разобьем обе трапеции на
треугольники, у которых площади и
положения центров тяжести легко
определяются.

Эпюра
M F

ω 1

C 1 C 2

ω 2

Эпюра

Мы
получили формулу
трапеций,
согласно
которой произведения соответствующих
левых и правых ординат эпюр необходимо
удвоить, а произведения перекрестных
ординат взять одинарными, и полученную
сумму умножить на одну шестую длины
эпюр.

Рассмотрим
случай, когда грузовая эпюра представлена
квадратной параболой, а единичная эпюра
– трапецией.

ω П.С.

Наряду
с крайними ординатами укажем и средние.

Разобьем
криволинейную эпюру на трапецию и
параболический сегмент.

Произведем
перемножение соответствующих фигур.

Выражение
I Т
у нас имеется. Найдем
.

Площадь
параболического сегмента:

Ордината
единичной эпюры под центром тяжести
параболического сегмента:

После
подстановки получаем формулу
Симпсона:

Произведение
двух эпюр равно сумме произведений
крайних ординат и учетверенному
произведению средних ординат, умноженной
на одну шестую длины эпюр.

§7. Силовой расчет статически неопределимых стержневых систем (снс).

Статически
неопределимые системы (СНС) имеют
преимущества и недостатки по сравнению
со статически определимыми системами
(СОС).

Достоинства:

СНС
обладают большей живучестью при
эксплуатации под нагрузкой, чем СОС. В
СОС все элементы практически
равнонапряжены, и поэтому они имеют
резервы прочности только в пределах
коэффициента запаса k
=1,5
– 2. Если хотя бы один элемент перейдет
в предельное состояние, вся конструкция
получит недопустимые с точки зрения
норм расчета деформации или разрушится.
СНС – это неравнонапряженная конструкция
и при переходе наиболее напряженного
элемента в предельное состояние,
происходит перераспределение усилий
от возросшей нагрузки на менее напряженные
элементы.

СНС,
в силу наличия лишних связей и избыточной
жесткости отдельных элементов, менее
деформативны, чем СОС, т.е. в них меньше
линейные угловые перемещения.

Недостатки:

СНС
более сложны в расчете, чем СОС, что
объясняется наличием избыточных
(лишних) связей. Трудоемкость расчета
СНС пропорциональна третьей степени
количества лишних связей, т.е.
.
Например, если для двух системn 1 =1,
n 2 =4 ,
то
t 1 = α ,
t 2 =64α ,
т.е. время расчета возрастает в 64 раза.

В
СНС распределение усилий в элементах
зависит от их геометрических размеров,
определение которых, в свою очередь,
является основной задачей сопротивления
материалов. Таким образом, возникает
необходимость априорного назначения
изгибных жесткостей и поперечных
сечений отдельных стержней: (EY ) k =α k (EY ),
что приводит к неоднозначности
конструктивных решений.

Более
удачные назначения жесткостей, зависящие
от понимания сущности задач сопротивления
материалов, приведет к созданию более
оптимальных конструкций.

В
СНС возможно появление трудно
предсказуемого по величине
напряженно-деформированного состояния,
вызванного температурными изменениями
и независимой осадкой опор. Изменение
температуры одного из элементов вызывает
появление температурных напряжений
во всех стержнях СНС. Равно как неточность
изготовления одного из стержней или
смещение одной связи вызывает появление
монтажных напряжений во всех стержнях.
В СОС таких напряжений не возникает.

Рассмотрим
основные методы расчета СНС при
статическом воздействии нагрузок.

Определение перемещений в системах, состоящих из прямолинейных элементов постоянной жесткости, можно значительно упростить путем применения специального приема вычисления интеграла вида . В связи с тем что в подынтегральное выражение входит произведение усилий являющихся ординатами эпюр, построенных для единичного и действительного состояний, этот прием называют способом перемножения эпюр.

Его можно использовать в случае, когда одна из перемножаемых эпюр, например прямолинейна; в этом случае (рис. Вторая эпюра может иметь любое очертание (прямолинейное, ломаное или криволинейное).

Подставим значение в выражение

где - дифференциал площади эпюры (рис. 17.11).

Интеграл представляет собой статический момент площади эпюры относительно оси (рис. 17.11).

Этот статический момент можно выразить иначе:

где - абсцисса центра тяжести площади эпюры

Но так как (см. рис. 17.11)

(26.11)

Таким образом, результат перемножения двух эпюр равен произведению площади одной из них на ординату другой (прямолинейной) эпюры, взятую под центром тяжести площади первой эпюры.

Способ перемножения эпюр предложен в 1925 г. студентом Московского института инженеров железнодорожного транспорта А. Н. Верещагиным, а потому он называется правилом (или способом ) Верещагина.

Заметим, что левая часть выражения (26.11) отличается от интеграла Мора отсутствием в ней жесткости сечения . Следовательно, результат выполненного по правилу Верещагина перемножения эпюр для определения искомого перемещения надо разделить на величину жесткости.

Очень важно отметить, что ордината должна быть взята обязательно из прямолинейной эпюры. Если обе эпюры прямолинейны, то ординату можно взять из любой эпюры. Так, если требуется перемножить прямолинейные эпюры и (рис. 18.11, а), то не имеет значения, что взять: произведение площади эпюры на ординату под ее центром тяжести из эпюры или произведение Qkyt площади Q эпюры на ординату под (или над) ее центром тяжести из эпюры

Когда перемножаются две эпюры, имеющие вид трапеции, то не надо находить положение центра тяжести площади одной из них. Следует одну из эпюр разбить на два треугольника и умножить площадь каждого из них на ординату под его центром тяжести из другой эпюры. Например, в случае, приведенном на рис. 18.11, б, получим

(27.11)

В круглых скобках этой формулы произведение левых ординат обеих эпюр и произведение правых ординат берутся с коэффициентом, равным двум, а произведения ординат, расположенных с разных сторон, - с коэффициентом, равным единице.

С помощью формулы (27.11) можно перемножать эпюры, имеющие вид «перекрученных» трапеций; при этом произведения ординат, имеющих одинаковые знаки, берутся со знаком плюс, а разные - минус. В случае, например, показанном на рис. 18.11, б, результат перемножения эпюр в виде «перекрученной» и обычной трапеций равен , а в случае, показанном на рис. 18.11, г, равен

Формула (27.11) применима и тогда, когда одна или обе перемножаемые эпюры имеют вид треугольника. В этих случаях треугольник рассматривается как трапеция с одной крайней ординатой, равной нулю. Результат, например, перемножения эпюр, показанных на рис. 18.11, д, равен

Умножение эпюры в виде «перекрученной» трапеции на любую другую эпюру можно производить и расчленяя «перекрученную трапецию на два треугольника, как показано на рис. 18.11, е.

Когда одна из эпюр (рис. 19.11) очерчена по квадратной параболе (от равномерно распределенной нагрузки q), то ее для перемножения с другой эпюрой рассматривают как сумму (в случае, показанном на рис. 19.11, а) или разность (в случае, показанном на рис. 19.11,б) трапецеидальной и параболической эпюр

Результат перемножения эпюр, показанных на рис. 19.11, а, равен после подстановки в него получаем

Результат перемножения эпюр, показанных на рис. 19.11,б, равен после подстановки в него - и получаем

В обоих полученных выражениях в скобках стоят суммы произведений крайних ординат обеих эпюр с учетверенным произведением средних ординат.

Встречаются случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но одна из них (или обе) ограничена ломаными прямыми линиями. В этих случаях для перемножения эпюр предварительно разбивают их на такие участки, в пределах каждого из которых по крайней мере одна эпюра прямолинейна. Так, например, при перемножении эпюр, показанных на рис. 20.11, а,б, можно разбить их на два участка и представить результат перемножения в виде суммы Можно, перемножая эти же эпюры, разбить их на три участка, как показано на рис. 20.11, в,г; в этом случае результат перемножения эпюр равен

При использовании правила Верещагина приходится вычислять площади различных геометрических фигур и определять положения их центров тяжести. В связи с этим в табл. 1.11 приведены значения площадей и координаты центров тяжести наиболее часто встречающихся геометрических фигур.

В качестве примера рассмотрим применение способа Верещагина для определения прогиба точки С (под силой ) балки, изображенной на рис. 16.11, а; при этом учтем действие изгибающих моментов и поперечных сил.

Единичное состояние балки, а также эпюры внутренних усилий в ней, вызванных нагрузкой и единичной силой показаны на рис. 16.11,б,б,г,д,е.

По формуле (24.11), используя способ Верещагина при перемножении эпюр, находим

Этот результат совпадает с результатом, полученным путем интегрирования.

Определим теперь горизонтальное смещение точки С рамы, изображенной на рис. 21.11, а. Моменты инерции поперечных сечений стоек рамы и ригеля указаны на рисунке; .

Действительное состояние рамы изображено на рис. 21.11, а. Эпюра изгибающих моментов для этого состояния (грузовая эпюра) показана на рис. 21.11, б.

В единичном состоянии к точке С рамы приложена в направлении искомого перемещения (т. е. горизонтального) сила, равная единице.

Таблица 1.11

(см. скан)

Эпюра изгибающих моментов М для этого состояния (единичная эпюра) изображена на рис. 21.11, в.

Знаки изгибающих моментов на эпюрах могут не указываться, так как известно, что ординаты эпюр отложены со стороны сжатых волокон каждого элемента.

Перемножив по способу Верещагина грузовую эпюру с единичной (рис. 21.11,б, в) и учтя при этом различные значения моментов инерции поперечных сечений стоек и ригеля рамы, найдем искомое перемещение точки С:

Знак минус при перемножении эпюр взят потому, что эпюры и М расположены с различных сторон элементов рамы, и, следовательно, изгибающие моменты и М имеют разные знаки.

Отрицательное значение полученного перемещения точки С означает, что эта точка смещается не по направлению единичной силы (рис. 21.11, в), а в противоположную сторону, т. е. вправо.

Приведем теперь некоторые практические указания по применению интеграла Мора к различным случаям вычисления перемещений.

Определение перемещений в балках, жесткость сечений которых постоянна по всей длине или в пределах отдельных участков, целесообразно производить, вычисляя интеграл Мора по правилу Верещагина. То же относится и к рамам из прямолинейных стержней постоянной или ступенчато-переменной жесткости.

При жесткости сечений элемента конструкции, непрерывно изменяющейся по его длине, перемещения должны определяться путем непосредственного (аналитического) вычисления интеграла Мора. Такую конструкцию можно рассчитать приближенно, заменив ее системой с элементами ступенчато-переменной жесткости, после чего для определения перемещений использовать способ Верещагина.

Способ Верещагина может применяться не только при определении перемещений, но и при определении потенциальной энергии.

УО «БГУИР»

кафедра инженерной графики

«ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА. ПРАВИЛО ВЕРЕЩАГИНА»

МИНСК, 2008

Рассмотрим теперь общий метод определения перемещений, пригодный для любой, линейно деформируемой системы при любой нагрузке. Этот метод предложен выдающимся немецким ученым О. Мором.

Пусть, например, требуется определить вертикальное перемещение точки А балки, представленной на рис. 7.13, а. Заданное (грузовое) состояние обозначим буквой к. Выберем вспомогательное состояние той же балки с единичной

силой, действующей в точке A и в направлении искомого перемещения. Вспомогательное состояние обозначим буквой i (рис. 7.13,6).

Вычислим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.

Работа внешних сил будет равна произведению единичной силы на искомое перемещение ya

а работа внутренних сил по абсолютной величине равна интегралу

(1)

Формула (7.33) и есть формула Мора (интеграл Мора), которая дает возможность определить перемещение в любой точке линейно-деформируемой системы.

В этой формуле подынтегральное произведение MiMk положительно, если оба изгибающих момента имеют одинаковый знак, и отрицательно, если Mi и Мк имеют разные знаки.

Если бы мы определяли угловое перемещение в точке А, то в состоянии i следовало бы приложить в точке А момент, равный единице (без размерности).

Обозначая буквой Δ любое перемещение (линейное или угловое), формулу (интеграл) Мора напишем в виде

(2)

В общем случае аналитическое выражение Mi и Мк может быть различным на разных участках балки или вообще упругой системы. Поэтому вместо формулы (2) следует пользоваться более общей формулой

(3)

Если стержни системы работают не на изгиб, а на растяжение (сжатие), как, например, в фермах, то формула Мора имеет вид

(4)

В этой формуле произведение NiNK положительно, если оба усилия растягивающие или оба сжимающие. Если стержни одновременно работают и на изгиб и на растяжение (сжатие), то в обычных случаях, как показывают сравнительные расчеты, перемещения можно определять, учитывая лишь изгибающие моменты, так как влияние продольных сил весьма мало.

По тем же соображениям, как отмечалось ранее, в обычных случаях можно не учитывать влияния поперечных сил.

Вместо непосредственного вычисления интеграла Мора можно пользоваться графо-аналитическим приемом «способом перемножения эпюр», или правилом Верещагина.

Рассмотрим две эпюры изгибающих моментов, из которых одна Мк имеет произвольное очертание, а другая Мi прямолинейна (Рис 7.14, а и б).

(5)

Величина MKdz представляет собой элементарную площадь dωk эпюры Мк (заштрихована на рисунке). Таким образом,

(6)

следовательно,

(8)

Но представляет собой статический момент площади эпюры Мк относительно некоторой оси у, проходящей через точку О, равный ωkzc, где ωk - площадь эпюры моментов; zс - расстояние от оси у до центра тяжести эпюры Мк. Из чертежа видно, что

где Мсi - ордината эпюры Mi, расположенная под центром тяжести эпюры Мк (под точкой С). Следовательно,

(10)

т. е. искомый интеграл равен произведению площади эпюры Мк (любой по очертанию) на расположенную под ее центром тяжести ординату прямолинейной эпюры Мсi. Значение величины ωкМсi считается положительным, если обе эпюры располагаются по одну сторону стержня, и отрицательным, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента).

Необходимо помнить, что ордината Мсi берется обязательно в прямолинейной эпюре. В том частном случае, когда обе эпюры прямолинейные, можно умножить площадь любой из них на соответствующую ординату другой.

Для стержней переменного сечения правило Верещагина перемножения эпюр неприменимо, так как в этом случае уже нельзя выносить величину EJ из-под знака интеграла. В этом случае следует выразить EJ как функцию абсциссы сечения и затем уже вычислять интеграл Мора (1).

При ступенчатом изменении жесткости стержня интегрирование (или перемножение эпюр) производят для каждого участка отдельно (со своим значением EJ) и затем суммируют результаты.

В табл. 1 приведены значения площадей некоторых простейших эпюр и координат их центра тяжести.

Таблица 1

Вид эпюры	Площадь эпюры	Расстояние до центра тяжести

Для ускорения вычислений можно использовать готовые таблицы перемножения эпюр (табл.2).

В этой таблице, в клетках на пересечении соответствующих элементарных эпюр, приведены результаты перемножения этих эпюр.

При разбивке сложной эпюры на элементарные, представленные в табл. 1 и 7.2, следует иметь в виду, что параболические эпюры получены от действия только одной распределенной нагрузки.

В тех случаях, когда в сложной эпюре криволинейные участки получаются от одновременного действия сосредоточенных моментов, сил и равномерно распределенной нагрузки, во избежание ошибки следует сложную эпюру предварительно «расслоить», т. е. разбить ее на ряд самостоятельных эпюр: от действия сосредоточенных моментов, сил и от действия равномерно распределенной нагрузки.

Можно также применить другой прием, не требующий расслоения эпюр, а требующий лишь выделения криволинейной части эпюры по хорде, соединяющей крайние ее точки.

Покажем оба способа на конкретном примере.

Пусть, например, требуется определить вертикальное перемещение левого конца балки (рис. 7.15).

Суммарная эпюра от нагрузки представлена на рис. 7.15, а.

Таблица 7.2

Эпюра от действия единичной силы в точке А представлена на рис. 7.15, г.

Для определения вертикального перемещения в точке А необходимо перемножить эпюру от нагрузки на эпюру от единичной силы. Однако замечаем, что на участке ВС суммарной эпюры криволинейная эпюра получена не только от действия равномерно распределенной нагрузки, но также и от действия сосредоточенной силы Р. В результате на участке ВС уже будет не элементарная параболическая эпюра, приведенная в таблицах 7.1 и 7.2, а по существу сложная эпюра, для которой данные этих таблиц недействительны.

Поэтому необходимо произвести расслоение сложной эпюры по рис. 7.15, а на элементарные эпюры, представленные на рис. 7.15, б и 7.15, в.

Эпюра по рис. 7.15, б получена только от сосредоточенной силы, эпюра по рис. 7.15, в - только от действия равномерно распределенной нагрузки.

Теперь можно перемножить эпюры, используя табл. 1 или 2.

Для этого необходимо перемножить треугольную эпюру по рис. 7.15, б на треугольную эпюру по рис. 7.15, г и добавить к этому результат перемножения параболической эпюры на рис. 7.15, в на трапециевидную эпюру участка ВС по рис. 7.15, г, так как на участке АВ ординаты эпюры по рис. 7.15, в равны нулю.

Покажем теперь второй способ перемножения эпюр. Рассмотрим снова эпюру по рис. 7.15, а. Примем начало отсчета в сечении В. Покажем, что в пределах кривой LMN изгибающие моменты могут быть получены как алгебраическая сумма изгибающих моментов, соответствующих прямой LN, и изгибающих моментов параболической эпюры LNML, такой же, как и для простой балки длиной а, загруженной равномерно распределенной нагрузкой q:

Наибольшая ордината посредине будет равна .

Для доказательства напишем фактическое выражение изгибающего момента в сечении на расстоянии z от точки В

(А)

Напишем теперь выражение изгибающего момента в том же сечении, полученное как алгебраическая сумма ординат прямой LN и параболы LNML.

Уравнение прямой LN

где k - тангенс угла наклона этой прямой

Следовательно, уравнение изгибающих моментов, полученное как алгебраическая сумма уравнения прямой LN и параболы LNMN имеет вид

что совпадает с выражением (А).

При перемножении эпюр по правилу Верещагина следует перемножить трапецию BLNC на трапецию из единичной эпюры на участке ВС (см. рис. 7.15, г) и вычесть результат перемножения параболической эпюры LNML (площадью ) на ту же трапецию из единичной эпюры. Такой способ расслоения эпюр особенно выгоден, когда криволинейный участок эпюры находится на одном из средних участков балки.

Пример 7.7. Определить вертикальное и угловое перемещения консольной балки в месте приложения нагрузки (рис. 7.16).

Решение. Строим эпюру изгибающих моментов для грузового состояния (рис. 7.16, а).

Для определения вертикального перемещения выбираем вспомогательное состояние балки с единичной силой в точке приложения нагрузки.

Строим эпюру изгибающих моментов от этой силы (рис. 7.16, б). Определяем вертикальное перемещение по способу Мора

Значение изгибающего момента от нагрузки

Значение изгибающего момента от единичной силы

Подставляем эти значения МР и Mi под знак интеграла и интегрируем

Этот же результат был ранее получен другим способом.

Положительное значение прогиба показывает, что точка приложения нагрузки Р перемещается вниз (в направлении единичной силы). Если бы мы единичную силу направили снизу вверх, то имели бы Mi = 1z и в результате интегрирования получили бы прогиб со знаком минус. Знак минус показывал бы, что перемещение происходит не вверх, а вниз, как это и есть в действительности.

Вычислим теперь интеграл Мора путем перемножения эпюр по правилу Верещагина.

Так как обе эпюры прямолинейны, то безразлично, из какой эпюры брать площадь и из какой - ординату.

Площадь грузовой эпюры равна

Центр тяжести этой эпюры расположен на расстоянии 1/3l от заделки. Определяем ординату эпюры моментов от единичной силы, расположенную под

центром тяжести грузовой эпюры. Легко убедиться, что она равна 1/3l.

Следовательно.

Тот же результат получается и по таблице интегралов. Результат перемножения эпюр положителен, так как обе эпюры располагаются снизу стержня. Следовательно, точка приложения нагрузки смещается вниз, т. е. по принятому направлению единичной силы.

Для определения углового перемещения (угла поворота) выбираем вспомогательное состояние балки, в котором на конце балки действует сосредоточенный момент, равный единице.

Строим эпюру изгибающих моментов для этого случая (рис. 7.16, в). Определяем угловое перемещение, перемножая эпюры. Площадь грузовой эпюры

Ординаты эпюры от единичного момента везде равны единице., Следовательно, искомый угол поворота сечения равен

Так как обе эпюры расположены снизу, то результат перемножения эпюр положителен. Таким образом, концевое сечение балки поворачивается по часовой стрелке (по направлению единичного момента).

Пример: Определить по способу Мора - Верещагина прогиб в точке D для балки, изображенной на рис. 7.17..

Решение. Строим расслоенную эпюру моментов от нагрузки, т. е. строим отдельные эпюры от действия каждой нагрузки. При этом для удобства перемножения эпюр целесообразно строить расслоенные (элементарные) эпюры относительно сечения, прогиб которого определяется в данном случае относительно сечения D.

На рис. 7.17, а представлена эпюра изгибающих моментов от реакции А (участок AD) и от нагрузки Р = 4 Т (участок DC). Эпюры строятся на сжатом волокне.

На рис. 7.17, б представлены эпюры моментов от реакции В (участок BD), от левой равномерно распределенной нагрузки (участок AD) и от равномерно распределенной нагрузки, действующей на участке ВС. Эта эпюра изображена на рис. 7.17, б на участке DC снизу.

Далее выбираем вспомогательное состояние балки, для чего в точке D, где определяется прогиб, прикладываем единичную силу (рис. 7.17, в). Эпюра моментов от единичной силы изображена на рис. 7.17, г. Теперь перемножим эпюры с 1 по 7 на эпюры 8 и 9, пользуясь таблицами перемножения эпюр, с учетом знаков.

При этом эпюры, расположенные с одной стороны балки, перемножаются со знаком плюс, а эпюры, расположенные по разные стороны балки, перемножаются со знаком минус.

При перемножении эпюры 1 и эпюры 8 получим

Перемножая эпюру 5 на эпюру 8, получим

Перемножение эпюр 2 и 9 дает

Перемножаем эпюры 4 и 9

Перемножаем эпюры 6 и 9

Суммируя результаты перемножения эпюр, получим

Знак минус показывает, что точка D перемещается не вниз, как направлена единичная сила, а вверх.

Этот же результат был получен ранее по универсальному уравнению.

Конечно, в данном примере можно было расслоить эпюру только на участке AD, так как на участке DB суммарная эпюра прямолинейная и ее незачем расслаивать. На участке ВС расслоения не требуется, так как от единичной силы на этом участке эпюра равна нулю. Расслоение эпюры на участке ВС необходимо для определения прогиба в точке С.

Пример. Определить вертикальное, горизонтальное и угловое перемещения сечения А ломаного стержня, представленного на рис. 7.18, а. Жесткость сечения вертикального участка стержня - EJ1 жесткость сечения горизонтального участка - EJ2.

Решение. Строим эпюру изгибающих моментов от нагрузки. Она представлена на рис. 7.18, б (см. пример 6.9). Для определения вертикального перемещения сечения А выбираем вспомогательное состояние системы, представленное на рис. 7.18, в. В точке А приложена единичная вертикальная сила, направленная вниз.

Эпюра изгибающих моментов для этого состояния представлена на рис. 7.18, в.

Определяем вертикальное перемещение по методу Мора, используя способ перемножения эпюр. Так как на вертикальном стержне во вспомогательном состоянии эпюра М1 отсутствует, то перемножаем только эпюры, относящиеся к горизонтальному стержню. Площадь эпюры берем из грузового состояния, а ординату - из вспомогательного. Вертикальное перемещение равно

Так как обе эпюры расположены снизу, то результат перемножения берем со знаком плюс. Следовательно, точка А перемещается вниз, т. е. так, как направлена единичная вертикальная сила.

Для определения горизонтального перемещения точки А выбираем вспомогательное состояние с горизонтальной единичной силой, направленной влево (рис. 7.18, г). Эпюра моментов для этого случая представлена там же.

Перемножаем эпюры МP и М2 и получаем

Результат перемножения эпюр положителен, так как перемножаемые эпюры располагаются на одной и той же стороне стержней.

Для определения углового перемещения выбираем вспомогательное состояние системы по рис. 7.18,5 и строим эпюру изгибающих моментов для этого состояния (на том же рисунке). Перемножаем эпюры МР и М3:

Результат перемножения положителен, так как перемножаемые эпюры располагаются с одной стороны.

Следовательно, сечение A поворачивается по часовой стрелке

Те же результаты получились бы и при использовании таблиц
перемножения эпюр.

Вид деформированного стержня показан на рис. 7.18, е, при этом перемещения сильно увеличены.

ЛИТЕРАТУРА

Феодосьев В.И. Сопротивление материалов. 1986

Беляев Н.М. Сопротивление материалов. 1976

Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем. 1991

Работнов Ю.Н. Механика деформируемого твердого тела. 1988

Степин П.А. Сопротивление материалов. 1990

А его собственноручные записки оказались в руках дьяка Посольского приказа, от которого и были получены. Иные сведения биографического характера извлекаются только из самого текста «Хожения». Почему же Афанасий Никитин назвал свое произведение «Хожением за три моря»? Автор сам дает нам ответ на этот вопрос: «Се написах свое грешное «Хожение за три моря», 1-е море Дербеньское (Каспийское), дория...

Отмечает, что непременным условием реализации любого коммуникативного акта должно быть «обоюдное знание реалий говорящим и слушающим, являющееся основой языкового общения», они получили в лингвистике название «фоновых знаний». По ее правильному замечанию «значение слова, употребляемого в данном туземном языке для обозначения таких совершенно различных с точки зрения среднеевропейской культуры...

Для балок и стержневых систем, состоящих из прямых стержней, внутренние усилия единичных состояний N k , M k и Q k являются линейными функциями или на всем протяжении каждого стержня, или на его отдельных участках. Внутренние усилия грузового состояния Np, М Р и Q P могут иметь произвольные законы изменения по длине стержней. Если балки и стержни имеют при этом постоянные или ступенчато-постоянные жесткости EF, EJ и GF, то вычисление интегралов в формуле Мора может быть произведено с помощью эпюр внутренних усилий.

Рассмотрим, например, эпюры изгибающих моментов М Р и М к в прямом стержне постоянной жесткости (рис. 8.31). Грузовая эпюра М Р является произвольной, а единичная эпюра М к - линейной. Начало отсчета координат поместим в точке пересечения линии эпюры М к с осью Ох. При этом изгибающий момент М к изменяется по закону М к = xtga. Вынося постоянную величину tga/ЕУв формуле (8.22) из-под знака интеграла и производя интегрирование по длине стержня, получим

Величина M P dx = dQ. P является элементом площади грузовой эпюры М р. При этом сам интеграл можно рассматривать как статический момент площади эпюры М Р относительно оси Оу, который равен

где Q. p - площадь эпюры х с - абсцисса ее центра тяжести. Учитывая, что x c tga = у с, получаем окончательный результат:

где у с - ордината в линейной эпюре М к под центром тяжести площади криволинейной эпюры М р (рис. 8.31).

Способ вычисления интегралов в формуле Мора с помощью формулы (8.23) называется правилом Верещагина или правилом «перемножения» эпюр. Согласно формуле (8.23) результат «перемножения» двух эпюр равен произведению площади нелинейной эпюры на ординату под ее центром тяжести в линейной эпюре. Если обе эпюры на рассматриваемом участке являются линейными, то при «перемножении» можно брать площадь любой из них. Результат «перемножения» однозначных эпюр является положительным, а разнозначных - отрицательным.

Результат «перемножения» двух трапеций (рис. 8.32) можно представить в виде следующей формулы:

При использовании правила Верещагина сложные эпюры надо разбить на простые фигуры, у которых известны площадь и положение центра тяжести. Чаще всего элементами разбиения являются треугольники и квадратные параболы (в случае действия равномерно распределенных нагрузок). Примеры разбиения эпюр приведены на рис. 8.33.

Однозначные или разнозначные трапеции можно разбить на два треугольника (рис. 8.33, а). Квадратная парабола с ординатами а и b в начале и конце участка разбивается на два однозначных или разнозначных треугольника и квадратную параболу с нулевыми начальным и конечным значениями (рис. 8.33, б). Ее площадь определяется по формуле

где q - интенсивность равномерно распределенной нагрузки.

Правило Верещагина нельзя применять в случае, когда обе эпюры являются нелинейными (например, для стержней с криволинейной осью), а также для стержней с переменной жесткостью EJ. В этом случае при определении перемещений методом Мора производится аналитическое или численное вычисление интегралов в формуле (8.20).

Пример 8.7. Для консольной балки постоянной жесткости EJ= const (рис. 8.34, а ) определим прогиб в сечении В и угол поворота сечения С.

Построим эпюру изгибающих моментов М Р от действия заданных нагрузок (рис. 8.34, б). Для определения искомых перемещений приложим в сечении В единичную силу Р = 1, в сечении С - единичный момент М = 1 и построим единичные эпюры М, и М 2 (рис. 8.34, в, г). Грузовую эпюру М р на втором участке разобьем на треугольник и квадратную параболу.

«Перемножим» грузовую и единичные эпюры между собой с помощью правила Верещагина. При «перемножении» эпюр М р и М х на первом участве используем формулу (8.24). В результате вычислений получим:

Направления перемещений совпадают с направлениями действия единичных нагрузок. Прогиб балки в сечении В происходит вниз, а сечение С поворачивается по ходу часовой стрелки.

Пример 8.8. Для шарнирно опертой балки постоянной жесткости (рис. 8.35, а) определим прогиб в сечении Си угол поворота сечения В.

Грузовая эпюра М р приведена на рис. 8.35, б. Приложим в сечении С единичную силу, в сечении В - единичный момент и построим единичные эпюры М х и М 2 (рис. 8.35, в, г). «Перемножив» грузовую эпюру М р с единичными эпюрами, найдем искомые перемещения:

При «перемножении» эпюр на втором участке использована формула (8.24). Сечение В

Пример 8.9. Для шарнирно опертой балки с консолью постоянной жесткости (рис. 8.36, а) определим прогиб в сечении С и угол поворота сечения D.

Определим опорные реакции от действия заданных нагрузок:

Построим грузовую эпюру М р (рис. 8.36, б). Соответствующие единичные эпюры приведены jHa рис. 8.36, в , г. «Перемножая» эпюру М Р с эпюрами М х и М 2 , найдем искомые перемещения:

Сечение С перемещается вверх, сечение D поворачивается против хода часовой стрелки.

Пример 8.10. Для балки ступенчато-постоянной жесткости с промежуточным шарниром (рис. 8.37, а) определим взаимный угол поворота и прогиб в сечении В.

Разобьем балку на несущую и несомую части (рис. 8.37, б) и определим опорные реакции для балки ЛВ

Грузовая эпюра М р и соответствующие единичные эпюры приведены на рис. 8.37, в , г, д. Отметим, что для определения взаимного угла поворота сечений в промежуточном шарнире приложен парный единичный момент (слева и справа от шарнира).

«Перемножая» эпюру М Р с единичными эпюрами и учитывая ступенчатое изменение жесткости на участках АВ и ВС, найдем:

Пример 8.11. Для консольной рамы со стержнями различной жесткости (рис. 8.38, я) определим вертикальное и горизонтальное перемещения точки С и угол поворота сечения В.

Эпюра МрОТ внешней нагрузки показана на рис. 8.38, б. Влияние продольных и поперечных сил при определении перемещений не учитываем.

Эпюры М х, М 2 и М 3 от единичных сил и момента, приложенных в сечениях С и В, показаны на рис. 8.38, в, г, д. «Перемножая» грузовую эпюру М р с единичными эпюрами в пределах длины каждого стержня, определим искомые перемещения:

Поворот сечения В происходит против хода часовой стрелки. Горизонтальное перемещение точки С равно нулю.

Пример 8.12. Для шарнирно опертой рамы со стержнями различной жесткости (рис. 8.39, а) определим вертикальное перемещение точки С и горизонтальное перемещение точки В.

Определим опорные реакции:

Грузовая и соответствующие единичные эпюры приведены на рис. 8.39, б, в, г. «Перемножив» эпюры в пределах длины каждого стержня, найдем:

В заключение приведем значения прогибов и углов поворота для консольных и шарнирно опертых балок при простых нагрузках.