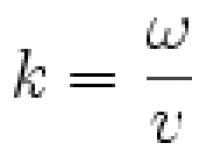Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где - некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде

где , и - некоторые числа.

Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний - это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус - периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем

Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).

Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.

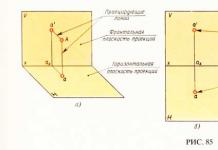
В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического ) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника

где - длина нити, - ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.

Чтобы найти циклическую частоту колебаний груза в задаче 11.1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с - это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c -1 (ответ 2 ). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний - 0,1 с -1 (ответ 1 ).

Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3 ), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия - одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону - вторая, назад в положение равновесия - третья, из положения равновесия в начальную точку - четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода - две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4 ).

Величина перемещения тела - расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3 ).

По определению фаза колебаний - это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 - 3 .

Период - это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (задача 11.1.6 ) тело затрачивает четвертую часть периода (ответ 3 ).

Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2 . Функция же - тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4 ).

При гармонических колебаниях скорость тела изменяется по закону , где - амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени
(задача 11.1.8 ). Используя далее известную тригонометрическую формулу, получаем

Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2 ).

За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9 ) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ 2 ).

Амплитуду колебаний скорости (задача 11.1.10 ) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где - коэффициент жесткости пружины, - амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где - масса тела, - скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим

(ответ 4 ).

Из формулы (11.5) заключаем (задача 11.2.2 ), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1 ).

Часы - это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3 ). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ 3 ).

Чтобы найти амплитуду колебаний в задаче 11.2.4 , необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим

где - такой угол, что . Из этой формулы следует, что амплитуда колебаний тела - (ответ 4 ).

Важнейшим параметром, характеризующим механические, звуковые, электрические, электромагнитные и все другие виды колебаний, является период - время, в течение которого совершается одно полное колебание. Если, например, маятник часов-ходиков делает за 1 с два полных колебания, период каждого колебания равен 0,5с. Период колебаний больших качелей около 2 с, а период колебаний струны может составлять от десятых до десятитысячных долей секунды.

Рисунок 2.4 - Колебание

где: φ – фаза колебания, I – сила тока, Ia – амплитудное значение силы тока (амплитуда)

Т – период колебания силы тока (период)

Другим параметром, характеризующим колебания, является частота (от слова «часто») - число, показывающее, сколько полных колебаний в секунду совершают маятник часов, звучащее тело, ток в проводнике и т.п. Частоту колебаний оценивают единицей, носящей название герц (сокращенно пишут Гц): 1 Гц-это одно колебание в секунду. Если, например, звучащая струна совершает 440 полных колебаний в 1 с (при этом она создает тон «ля» третьей октавы), говорят, что частота ее колебаний 440 Гц. Частота переменного тока электроосветительной сети 50 Гц. При этом токе электроны в проводах сети в течение секунды текут попеременно 50 раз в одном направлении и столько же раз в обратном, т.е. совершают за 1 с 50 полных колебаний.

Более крупные единицы частоты - килогерц (пишут кГц), равный 1000 Гц и мегагерц (пишут МГц), равный 1000 кГц или 1 000 000 Гц.

Амплитуда - максимальное значение смещения или изменения переменной величины при колебательном или волновом движении. Неотрицательная скалярная величина, измеряется в единицах, зависящих от типа волны или колебания.

Рисунок 2.5 - Синусоидальное колебание.

где, y - амплитуда волны, λ - длина волны.

Например:

амплитуда для механического колебания тела (вибрация), для волн на струне или пружине - это расстояние и записывается в единицах длины;

амплитуда звуковых волн и аудио-сигналов обычно относится к амплитуде давления воздуха в волне, но иногда описывается как амплитуда смещения относительно равновесия (воздуха или диафрагмы говорящего). Её логарифм обычно измеряется в децибелах (дБ);

для электромагнитного излучения амплитуда соответствует величине электрического и магнитного поля.

Форма изменения амплитуды называется огибающей волной .

Звуковые колебания

Как возникают звуковые волны в воздухе? Воздух состоит из невидимых глазам частиц. При ветре они могут переноситься на большие расстояния. Но они, кроме того, могут и колебаться. Например, если в воздухе сделать резкое движение палкой, то мы почувствуем легкий порыв ветра и одновременно услышим слабый звук. Звук это - результат колебаний частиц воздуха, возбужденных колебаниями палки.

Проведем такой опыт. Оттянем струну, например, гитары, а потом отпустим ее. Струна начнет дрожать - колебаться около своего первоначального положения покоя. Достаточно сильные колебания струны заметны на глаз. Слабые колебания струны можно только почувствовать как легкое щекотание, если прикоснуться к ней пальцем. Пока струна колеблется, мы слышим звук. Как только струна успокоится, звук затихнет. Рождение звука здесь - результат сгущения и разрежения частиц воздуха. Колеблясь из стороны в сторону, струна теснит, как бы прессует перед собой частицы воздуха, образуя в некотором его объеме области повышенного давления, а сзади, наоборот, области пониженного давления. Это и есть звуковые волны . Распространяясь в воздухе со скоростью около 340 м/с , они несут в себе некоторый запас энергии. В тот момент, когда до уха доходит область повышенного давления звуковой волны, она надавливает на барабанную перепонку, несколько прогибая ее внутрь. Когда же до уха доходит разреженная область звуковой волны, барабанная перепонка выгибается несколько наружу. Барабанная перепонка все время колеблется в такт с чередующимися областями повышенного и пониженного давления воздуха. Эти колебания передаются по слуховому нерву в мозг, и мы воспринимаем их как звук. Чем больше амплитуды звуковых волн, тем больше энергии несут они в себе, тем громче воспринимаемый нами звук.

Звуковые волны, как и водяные или электрические колебания, изображают волнистой линией - синусоидой. Ее горбы соответствуют областям повышенного давления, а впадины-областям пониженного давления воздуха. Область повышенного давления и следующая за нею область пониженного давления образуют звуковую волну.

По частоте колебаний звучащего тела можно судить о тоне или высоте звука. Чем больше частота, тем выше тон звука, и наоборот, чем меньше частота, тем ниже тон звука. Наше ухо способно реагировать на сравнительно небольшую полосу (участок) частот звуковых колебаний - примерно от 20 Гц до 20 кГц . Тем не менее эта полоса частот вмещает всю обширнейшую гамму звуков, создаваемых голосом человека, симфоническим оркестром: от очень низких тонов, похожих на звук жужжания жука, до еле уловимого высокого писка комара. Колебания частотой до 20 Гц, называемые инфразвуковыми , и свыше 20 кГц, называемые ультразвуковыми , мы не слышим. А если бы барабанная перепонка нашего уха оказалась способной реагировать и на ультразвуковые колебания, мы могли бы тогда услышать писк летучих мышей, голос дельфина. Дельфины издают и слышат ультразвуковые колебания с частотами до 180 кГц.

Но нельзя путать высоту, т.е. тон звука с его силой. Высота звука зависит не от амплитуды, а от частоты колебаний. Толстая и длинная струна музыкального инструмента, например, создает низкий тон звука, т.е. колеблется медленнее, чем тонкая и короткая струна, создающая высокий тон звука (рис. 1).

Рисунок 2.6 - Звуковые волны

Чем больше частота колебаний струны, тем короче звуковые волны и выше тон звука.

В электро - и радиотехнике используют переменные токи частотой от нескольких герц до тысяч гигагерц. Антенны широковещательных радиостанций, например, питаются токами частотой примерно от 150 кГц до 100 МГц.

Эти быстропеременные колебания, называемые колебаниями радиочастоты, и являются тем средством, с помощью которого осуществляется передача звуков на большие расстояния без проводов.

Весь огромный диапазон переменных токов принято подразделять на несколько участков - поддиапазонов.

Токи частотой от 20 Гц до 20 кГц, соответствующие колебаниям, воспринимаемым нами как звуки разной тональности, называют токами (или колебаниями) звуковой частоты , а токи частотой выше 20 кГц - токами ультразвуковой частоты .

Токи частотой от 100 кГц до 30 МГц называют токами высокой частоты ,

Токи частотой выше 30 МГц - токами ультравысокой и сверхвысокой частоты.

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна - это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

Так и к ангармоническим строго периодическими колебаниям (а приближенно - с тем или иным успехом - и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием , под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: T {\displaystyle T} (хотя могут применяться и другие, наиболее часто это τ {\displaystyle \tau } , иногда Θ {\displaystyle \Theta } и т. д.).

Для волновых процессов период связан кроме того очевидным образом с длиной волны λ {\displaystyle \lambda }

где v {\displaystyle v} - скорость распространения волны (точнее - фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта - например, частицы - есть частота колебаний его волновой функции).

Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно - и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы , секундомеры , частотомеры , стробоскопы , строботахометры, осциллографы . Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса . Для волн можно померить период косвенно - через длину волны, для чего применяются интерферометры , дифракционные решетки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Энциклопедичный YouTube

• 1 / 5

  Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

  Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .

  Периоды колебаний слышимого человеком звука находятся в диапазоне

  От 5·10 −5 до 0,2

  (четкие границы его несколько условны).

  Периоды электромагнитных колебаний, соответствующих разным цветам видимого света - в диапазоне

  От 1,1·10 −15 до 2,3·10 −15 .

  Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекания в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней - период колебаний волновой функции самой тяжелой из известных сейчас частиц ().

  В любом случае границей снизу может служить планковское время , которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено , но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже намного порядков больших, а границей сверху - время существования Вселенной - более десяти миллиардов лет.

  Периоды колебаний простейших физических систем

  Пружинный маятник

  Математический маятник

  T = 2 π l g {\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}

  где l {\displaystyle l} - длина подвеса (к примеру, нити), g {\displaystyle g} - ускорение свободного падения .

  Период малых колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью равен 2 секундам.

  Физический маятник

  T = 2 π J m g l {\displaystyle T=2\pi {\sqrt {\frac {J}{mgl}}}}

  где J {\displaystyle J} - момент инерции маятника относительно оси вращения, m {\displaystyle m} -

  1. Вспомним, что называется частотой и периодом колебаний.

  Время, за которое маятник совершает одно полное колебание, называют периодом колебаний.

  Период обозначают буквойT и измеряют в секундах (с).

  Число полных колебаний за одну секунду, называют частотой колебаний. Частоту обозначают буквой n.

  1 Гц = .

  Единица частоты колебаний в Ш - герц (1 Гц ).

  1 Гц - это частота таких колебаний, при которых за 1 с совершается одно полное колебание .

  Частота колебаний и период связаны соотношением:

  n = .

  2. Период колебаний рассмотренных нами колебательных систем - математического и пружинного маятников - зависит от характеристик этих систем.

  Выясним, от чего зависит период колебаний математического маятника. Для этого проделаем опыт. Будем менять длину нити математического маятника и измерять время нескольких полных колебаний, например 10. В каждом случае определим период колебаний маятника, разделив измеренное время на 10. Опыт показывает, что чем больше длина нити, тем больше период колебаний.

  Теперь поместим под маятником магнит, увеличивая тем самым силу тяжести, действующую на маятник, и измерим период его колебаний. Заметим, что период колебаний уменьшится. Следовательно, период колебаний математического маятника зависит от ускорения свободного падения: чем оно больше, тем меньше период колебаний.

  Формула периода колебаний математического маятника имеет вид:

  T = 2p,

  где l - длина нити маятника, g - ускорение свободного падения.

  3. Определим экспериментально, от чего зависит период колебаний пружинного маятника.

  Будем подвешивать к одной и той же пружине грузы разной массы и измерять период колебаний. Заметим, что чем больше масса груза, тем больше период колебаний.

  Затем будем к пружинам разной жесткости подвешивать один и тот же груз. Опыт показывает, что чем больше жесткость пружины, тем меньше период колебаний маятника.

  Формула периода колебаний пружинного маятника имеет вид:

  T = 2p,

  где m - масса груза, k - жесткость пружины.

  4. В формулы периода колебаний маятников входят величины, характеризующие сами маятники. Эти величины называют параметрами колебательных систем.

  Если в процессе колебаний параметры колебательной системы не меняются, то период (частота) колебаний остается неизменным. Однако в реальных колебательных системах действуют силы трения, поэтому период реальных свободных колебаний с течением времени уменьшается.

  Если же предположить, что трение отсутствует и система совершает свободные колебания, то период колебаний меняться не будет.

  Свободные колебания, которые могла бы совершать система в отсутствие трения, называют собственными колебаниями.

  Частота таких колебаний называется собственной частотой . Она зависит от параметров колебательной системы.

  Вопросы для самопроверки

  1. Что называют периодом колебаний маятника?

  2. Что называют частотой колебаний маятника? Какова единица частоты колебаний?

  3. От каких величин и как зависит период колебаний математического маятника?

  4. От каких величин и как зависит период колебаний пружинного маятника?

  5. Какие колебания называют собственными?

  Задание 23

  1. Каков период колебаний маятника, если 20 полных колебаний он совершает за 15 с?

  2. Чему равна частота колебаний, если период колебаний равен0,25 с?

  3. Какой должна быть длина маятника в маятниковых часах, чтобы период его колебаний был равен 1 с? Считать g = 10 м/с 2 ; p 2 = 10.

  4. Чему равен период колебаний маятника, длина нити которого равна 28 см, на Луне? Ускорение свободного падения на Луне 1,75 м/с 2 .

  5. Определите период и частоту колебаний пружинного маятника, если жесткость его пружины равна 100 Н/м, а масса груза 1 кг.

  6. Во сколько раз изменится частота колебаний автомобиля на рессорах, если в него положить груз, масса которого равна массе ненагруженного автомобиля?

  Лабораторная работа № 2

  Изучение колебаний
  математического и пружинного маятников

  Цель работы:

  исследовать, от каких величин зависит, а от каких не зависит период колебаний математического и пружинного маятников.

  Приборы и материалы:

  штатив, 3 груза разной массы (шарик, груз массой 100 г, гирька), нить длиной 60 см, 2 пружины разной жесткости, линейка, секундомер, полосовой магнит.

  Порядок выполнения работы

  1. Изготовьте математический маятник. Наблюдайте его колебания.

  2. Исследуйте зависимость периода колебаний математического маятника от длины нити. Для этого определите время 20 полных колебаний маятников длиной 25 и 49 см. Вычислите период колебаний в каждом случае. Результаты измерений и вычисленийс учетом погрешности измерений занесите в таблицу 10. Сделайте вывод.

  Таблица 10

  l , м	n	t д Dt, с	T д DT, с
  0,25	20
  0,49	20

  3. Исследуйте зависимость периода колебаний маятника от ускорения свободного падения. Для этого под маятником длиной 25 см поместите полосовой магнит. Определите период колебаний, сравните его с периодом колебаний маятника в отсутствие магнита. Сделайте вывод.

  4. Покажите, что период колебаний математического маятника не зависит от массы груза. Для этого к нити неизменной длины подвешивайте грузы разной массы. Для каждого случая определите период колебаний, сохраняя одинаковой амплитуду. Сделайте вывод.

  5. Покажите, что период колебаний математического маятника не зависит от амплитуды колебаний. Для этого маятник отклоните сначала на 3 см, а затем на 4 см от положения равновесия и определите период колебаний в каждом случае. Результаты измерений и вычислений занесите в таблицу 11. Сделайте вывод.

  Таблица 11

  A , см	n	t + Dt , с	T + DT , с

  6. Покажите, что период колебаний пружинного маятника зависит от массы груза. Прикрепляя к пружине грузы разной массы, определите период колебаний маятника в каждом случае, измерив время 10 колебаний. Сделайте вывод.

  7. Покажите, что период колебаний пружинного маятника зависит от жесткости пружины. Сделайте вывод.

  8. Покажите, что период колебаний пружинного маятника не зависит от амплитуды. Результаты измерений и вычислений занесите в таблицу 12. Сделайте вывод.

  Таблица 12

  A , см	n	t + Dt , с	T + DT , с

  Задание 24

  1 э. Исследуйте область применимости модели математического маятника. Для этого изменяйте длину нити маятника и размеры тела. Проверьте, зависит ли период колебаний от длины маятника, если тело имеет большие размеры, а длина нити мала.

  2. Вычислите длины секундных маятников, установленных на полюсе (g = 9,832 м/с 2), на экваторе (g = 9,78 м/с 2), в Москве (g = 9,816 м/с 2), в Санкт‑Петербурге (g = 9,819 м/ с 2).

  3 * . Как влияют изменения температуры на ход маятниковых часов?

  4. Как изменится частота маятниковых часов при подъеме в гору?

  5 * . Девочка качается на качелях. Изменится ли период колебаний качелей, если на них сядут две девочки? Если девочка будет качаться не сидя, а стоя?

  Лабораторная работа № 3*

  Измерение ускорения свободного падения
  с помощью математического маятника

  Цель работы:

  научиться измерять ускорение свободного падения, используя формулу периода колебаний математического маятника.

  Приборы и материалы:

  штатив, шарик с прикрепленной к нему нитью, измерительная лента, секундомер (или часы с секундной стрелкой).

  Порядок выполнения работы

  1. Подвесьте к штативу шарик на нити длиной 30 см.

  2. Измерьте время 10 полных колебаний маятника и вычислите его период колебаний. Результаты измерений и вычисления занесите в таблицу 13.

  3. Пользуясь формулой периода колебаний математического маятника T = 2p, вычислите ускорение свободного падения по формуле: g = .

  4. Повторите измерения, изменив длину нити маятника.

  5. Вычислите относительную и абсолютную погрешность изменения ускорения свободного падения для каждого случая по формулам:

  dg ==+ ; Dg = g dg .

  Считайте, что погрешность измерения длины равна половине цены деления измерительной ленты, а погрешность измерения времени - цене деления секундомера.

  6. Запишите значение ускорения свободного падения в таблицу 13 с учетом погрешности измерений.

  Таблица 13

  № опыта	l д Dl , м	n	t д Dt , с	T д DT , с	g , м/с2	Dg , м/с2	g д Dg , м/с2

  Задание 25

  1. Изменится ли, и если да, то как, погрешность измерения периода колебаний маятника, если увеличить число колебаний с 20 до 30?

  2. Как влияет на точность измерения ускорения свободного падения увеличение длины маятника? Почему?