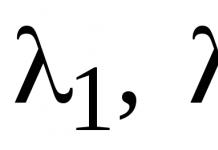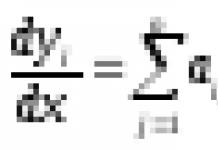7.1. Понятие устойчивости САУ

Понятие устойчивости является важнейшей качественной оценкой динамических свойств САР. Устойчивость САР связана с характером её поведения после прекращения внешнего воздействия, которое может быть оценено решением дифференциального уравнения, описывающего работу системы. Общая теория устойчивости разработана А.М. Ляпуновым. Линейная система называется устойчивой, если ее выходная координата остается ограниченной при любых ограниченных по абсолютной величине входных воздействиях. Устойчивость линейной системы определяется ее характеристиками и не зависит от действующих воздействий.
В общем случае решение уравнения имеет вид: y(t)= y B (t) + y n (t)
где y B (t) - решение однородного уравнения (переходная или свободная составляющая); y n (t) - установившееся значение регулируемой величины (вынужденная составляющая) - решение уравнения с правой частью. Устойчивость работы системы определяется переходной составляющей. Если переходная составляющая процесса управления после прекращения внешнего воздействия стремится к нулю, то такая система является устойчивой. Другими словами устойчивость системы - это есть затухание ее переходных процессов.
Если свободная составляющая стремится к конечному значению или имеет вид гармонических колебаний с постоянной амплитудой, то система считается нейтральной. В том случае, если свободная составляющая неограниченно возрастает или имеет вид гармонических колебаний с возрастающей амплитудой, то система считается неустойчивой.
Оценка устойчивости производится на основе результатов исследования свободной составляющей, которая представляет собой решение однородного дифференциального уравнения (характеристического уравнения): D(p) = a 0 p n + a 1 p n-1 + ... + a n = 0 (4.1)
Переходная составляющая решения уравнения в общем виде y ni (t) = A i e α i t * sin(β i t + φ i) , где α i ± jβ i - корни характеристического уравнения; A i ,Φ i - постоянные.
При этом переходная составляющая с ростом времени стремится к нулю, если вещественные части корней α i отрицательны, в противном случае амплитуда колебаний переходной составляющей возрастает (рис.4.1).

Рис.4.1. Графики переходных составляющих

Пара мнимых корней (α i =0) характеристического уравнения позволяет получить переходную составляющую в виде автоколебаний с постоянной амплитудой:

Полученные корни характеристического уравнения могут быть представлены в виде точек на комплексной плоскости (рис.4.2.).

Рис.4.2. Расположение корней САУ на комплексной плоскости корней

Для устойчивых систем необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости корней. Если хотя бы один вещественный корень или пара комплексных сопряженных корней находится справа от мнимый оси, то система является неустойчивой. Если имеется нулевой корень или пара чисто мнимых корней, то система считается нейтральной (находящейся на границе устойчивости и неустойчивости). Таким образом, мнимая ось комплексной плоскости является границей устойчивости.

С целью упрощения анализа устойчивости систем разработаны ряд специальных методов, которые получили название критерии устойчивости. Критерии устойчивости делятся на две разновидности: алгебраические (критерий Гурвица ) и частотные (критерии Михайлова и Найквиста ). Алгебраические критерии являются аналитическими, а частотные - графоаналитическими. Критерии устойчивости позволяют также оценить влияние параметров системы на устойчивость.

Алгебраический критерий Гурвица находит широкое применение при анализе САР. Первоначально, из коэффициентов уравнения (4.1) составляется матрица главного определителя:

По диагонали матрицы от верхнего левого угла записываются по порядку все коэффициенты уравнения (4.1.), начиная с а1. Затем каждый столбец матрицы дополняется таким образом, чтобы вверх от диагонали индексы коэффициентов увеличивались, а вниз - уменьшались.
Для устойчивости системы необходимо и достаточно, чтобы при а0>0 все угловые определители (миноры) были также положительными, т.е.

и т.д.

Последний определитель Гурвица, как видно из приведенной выше матрицы, равен Δ n =a n *Δ n-1 . Поэтому его положительность сводится при Δ n-1 >0 к условию a n >0. Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов ai. Если определитель Δ n =0, то система находится на границе устойчивости. Из условия Δ n-1 =0 можно определить параметры, при которых система находится на границе устойчивости, например, критический коэффициент усиления разомкнутой САУ К кр.

Критерий Михайлова предполагает построение годографа на комплексной плоскости. Для построения годографа из характеристического уравнения замкнутой системы (4.1) путем подстановки p=jω получают аналитическое выражение вектора M(jω):
M(jω)=a 0 (jω) n +a 1 (jω) n-1 +...+a n (4.2)
Уравнение (4.2) является комплексным и может быть представлено в виде:

Построение годографа производится по уравнению вектора M(jω) при изменении часты от 0 до + . Оценка устойчивости системы осуществляется по углу поворота годографа при изменении частоты 0<ω< , т.е. по приращению Δ аргумента M(jω)

, (4.3)

где m - число правых корней характеристического полинома; n - порядок характеристического уравнения системы.
Тогда для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента годографа M(jω) при изменении от 0 до + равнялось n , так как m=0 для обеспечения устойчивости системы.
Критерий Михайлова формулируется так: система устойчива, если годограф Михайлова M(jω) при изменении от 0 до + , начинаясь на положительной части действительной оси, обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов и в n-м квадранте уходил в .
Если годограф начинается в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной. В этом случае P(ω) = 0 и Q(ω) = 0.
Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости (критические значения). На рис.4.3 приведены годографы Михайлова для устойчивых и неустойчивых САУ.

Рис.4.3. Годографы Михайлова

Имеется вторая формулировка критерия Михайлова: для устойчивости системы необходимо и достаточно, чтобы корни уравнений P(ω) = 0 и Q(ω) = 0 перемежались (чередовались), т.е. годограф последовательно пересекал оси комплексной плоскости. Этой формулировкой удобно пользоваться для исследования устойчивости систем до пятого порядка включительно. По уравнению (4.3) можно определить количество правых корней в неустойчивых системах.

7.4. Частотный критерий устойчивости Найквиста

Критерий Найквиста - частотный критерий, позволяющий по виду амплитудно-фазовой частотной характеристики разомкнутой системы оценить устойчивость работы замкнутой системы. АФЧХ может быть получена экспериментально или аналитически. Аналитическое построение АФЧХ производится обычными методами. Критерий Найквиста формулируется по разному в зависимости от того, устойчива разомкнутая система или нет.
Если разомкнутая система устойчивая, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до не охватывала точку с координатами -I, j0. Если АФЧХ разомкнутой системы проходит через точку с координатами -I, j0, то система будет нейтральной. На рис.4.4 представлены АФЧХ разомкнутых статических систем. Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы.

Рис.4.4. АФЧХ разомкнутых САУ

АФЧХ астатической системы, начинаясь на вещественной положительной полуоси, при ω->0 дугой бесконечно большого радиуса перемещается на угол, равный -ν , где ν - порядок астатизма. На рис.4.5 изображена АФЧХ устойчивой в замкнутом состоянии астатической системы первого порядка.

Рис.4.5. АФЧХ астатической САУ первого порядка

Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы охватывала точку с координатами (-1, j0) и при изменении частоты от 0 до оборачивалась вокруг нее против часовой стрелки m раз, где m - число правых полюсов разомкнутой системы.
Существуют два класса САУ: абсолютно устойчивые и условно устойчивые. В первом классе систем только увеличение коэффициента усиления разомкнутой системы может привести к потере устойчивости, а условно устойчивая система может стать неустойчивой как при увеличении, так и при уменьшении коэффициента усиления.
Для абсолютно устойчивых систем вводится понятие запаса устойчивости по амплитуде (модулю) и запаса устойчивости по фазе. Запасы устойчивости определяют на частоте среза ω ср, на которой A(ω ср)=1.
Запас устойчивости по амплитуде задается некоторой величиной 1/а (рис.4.6), которая показывает, во сколько раз можно увеличить коэффициент усиления разомкнутой системы, чтобы САУ оказалась на границе устойчивости.

Рис.4.6. АФЧХ абсолютно устойчивой системы

Запас устойчивости по фазе задается некоторым углом φ (рис.4.6). В хорошо демпфированных системах запас устойчивости по амплитуде составляет примерно 6-20 дБ, что составляет 2÷10 в линейном масштабе, а запас по фазе от 30 до 60°.
Наиболее удобно для исследования устойчивости использовать построенные л.а.х. и л.ф.х., располагая их друг под другом так, чтобы оси ординат совмещались и выбирая одинаковые масштабы оси абсцисс (рис.4.7).

Рис.4.7. ЛЧХ абсолютно устойчивой системы

По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе φ зап отсчитывается по л.ф.х. на частоте среза ω ср и равен φ зап =π - φ(ω ср), а запас по амплитуде L зап соответствует значению л.а.х. на частоте, при которой л.ф.х. равна -π (рис.4.7). Если φ(ω ср)=-&pi, то система находится на границе устойчивости. Критический коэффициент усиления разомкнутой системы K кр определяется из выражения 20*lg(K кр)=20*lg(K раз) + L зап.
Критерием Найквиста удобно пользоваться для исследования устойчивости систем с запаздыванием. В этом случае строятся ЛЧХ разомкнутой САУ с запаздыванием W τ (jω) = W(jω) * e -jωτ . Логарифмическая частотная характеристика не изменяется, а л.ф.х. сдвигается вниз на величину -ω i τ, где ω i - значение частоты в конкретной точке. Критическое значение времени чистого запаздывания τ кр, при котором САУ будет на границе устойчивости, находится по формуле: .
Чтобы спроектировать систему с заданными показателями качества, строят запретную область вокруг точки с координатами (-1, j0), в которую не должна заходить АФЧХ разомкнутой системы, как показано на рис.4.8.

7.5. Логарифмический частотный критерий.

Логарифмический критерий – это частотный критерий, позволяющий судить об устойчивости замкнутой САУ по виду логарифмической характеристики разомкнутой системы. Этот критерий основан на однозначной связи ЛФЧХ и АФЧХ систем автоматического управления. При этом рассматриваются САУ, базирующиеся на использовании устойчивых разомкнутых систем. Кроме того, рассматриваются системы с астатизмом не выше второго порядка.

Как следует из критерия устойчивости Найквиста в устойчивых САУ фазовый сдвиг может достигать значения только при модулях комплексной передаточной функции, меньшем чем единица. Это позволяет легко определить устойчивость по виду ЛАЧХ и ЛФЧХ.

Формулировка критерия : для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы в диапазоне частот, где ЛАЧХ разомкнутой системы больше нуля число переходов фазовой характеристики прямой снизу верх превышало на число переходов сверху вниз, где а – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

В частном случае для устойчивой разомкнутой системы (а=0) необходимым и достаточным условием замкнутой системы является необходимость выполнения следующего условия. В диапазоне частот, где , фазовая частотная характеристика не должна пересекать прямой , или пересекать ее одинаковое число раз снизу вверх и сверху вниз.

Рис. 6. ЛФЧХ устойчивой и неустойчивой САУ

Критическим значением коэффициента преобразования называется такое его значение, при котором АФЧХ проходит через точку (-1, j0) и система находится на границе устойчивости.

Запасом по модулю называется величина в децибеллах, на которую нужно изменить коэффициент преобразования САУ, чтобы привести ее к границе устойчивости.

,

где - частота, при которой фазовая характеристика равна .

Запасом устойчивости по фазе называется угол, на который нужно повернуть амплитудно-фазовую характеристику разомкнутой системы, чтобы замкнутая САУ оказалась на границе устойчивости.

,

где – значение ФЧХ на частоте среза системы, для которой выполняется условие .

В этом разделе рассматриваются важнейшие характеристики качества управляемых систем. Этими характеристиками являются устойчивость систем, точность и помехоустойчивость.

Понятие устойчивости относится к ситуации, когда входные сигналы системы равны нулю, т.е. внешние воздействия отсутствуют. При этом правильно построенная система должна находиться в состоянии равновесия (покоя) или постепенно приближаться к этому состоянию. В неустойчивых системах даже при нулевых входных сигналах возникают собственные колебания и, как следствие, – недопустимо большие ошибки.

Понятие точности связано с качеством работы управляемых систем при изменяющихся входных сигналах. В правильно спроектированных системах управления величина рассогласования между заданным законом управления g(t) и выходным сигналом x(t) должна быть мала.

Наконец, для характеристики влияния помех на системы управления используют дисперсию или среднее квадратическое отклонение составляющей ошибки за счет действия помех.

Понятие устойчивости

Одним из первых вопросов, возникающих при исследовании и проектировании линейных систем управления, является вопрос об их устойчивости. Линейная система называется устойчивой , если при выведении ее внешними воздействиями из состояния равновесия (покоя) она возвращается в него после прекращения внешних воздействий. Если после прекращения внешнего воздействия система не возвращается к состоянию равновесия, то она является неустойчивой . Для нормального функционирования системы управления необходимо, чтобы она была устойчивой, так как в противном случае в ней возникают большие ошибки.

Определение устойчивости обычно проводят на начальном этапе создания системы управления. Это объясняется двумя причинами. Во-первых, анализ устойчивости довольно прост. Во-вторых, неустойчивые системы могут быть скорректированы, т.е. преобразованы в устойчивые с помощью добавления специальных корректирующих звеньев.

Анализ устойчивости с помощью алгебраических критериев

Устойчивость системы связана с характером ее собственных колебаний. Чтобы пояснить это, предположим, что система описывается дифференциальным уравнением

или, после преобразования Лапласа,

где g(p) – входное воздействие.

Устойчивая система возвращается в состояние покоя, если входное воздействие g(p) 0 . Таким образом, для устойчивой системы решение однородного дифференциального уравнения должно стремиться к нулю при t стремящемся к бесконечности.

Если найдены корни p1, p2, ... , pn характеристического уравнения , то решение однородного уравнения запишется в виде .

В каких же случаях система устойчива?

Предположим, что pk = ak – действительный корень.

Ему соответствует слагаемое ck. При ak < 0 это слагаемое будет стремиться к нулю, если t стремится к бесконечности. Если же ak > 0, то x(t) , когда t стремится к бесконечности; . Наконец, в том случае, когда ak = 0, рассматриваемое слагаемое не изменяется и при t стремящемся к бесконечности,

Допустим теперь, что – комплексный корень характеристического уравнения. Заметим, что в этом случае также будет корнем характеристического уравнения. Двум комплексно-сопряженным корням будут соответствовать слагаемые вида , .

При этом, если ak < 0, то в системе имеются затухающие колебания. При ak > 0 – колебания возрастающей амплитуды, а при ak = 0 -колебания постоянной амплитуды сk.

Таким образом, система устойчива, если действительные части всех корней характеристического уравнения отрицательны. Если хотя бы один корень имеет действительную часть ak ³ 0, то система неустойчива. Говорят, что система находится на границе устойчивости, если хотя бы один корень характеристического уравнения имеет нулевую действительную часть, а действительные части всех остальных корней отрицательны.

Это определение хорошо иллюстрируется геометрически. Представим корни характеристического уравнения точками на комплексной плоскости (рис. 15).

Если все корни лежат в левой полуплоскости комплексного переменного, то система устойчива. Если хотя бы один корень лежит в правой полуплоскости комплексного переменного - система неустойчива. Если же корни находятся на мнимой оси и в левой полуплоскости, то говорят, что система находится на границе устойчивости.

Рассмотрим в качестве примера замкнутую систему управления c одним интегрирующим звеном. В этом случае H(p) = , , а передаточная функция замкнутой системы

.

Выходной сигнал системы x(p) = W(p)g(p) или . Заметим, что характеристическое уравнение p+k=0 записывается с помощью приравнивания к нулю знаменателя передаточной функции замкнутой системы управления. В данном случае имеется один корень p1= -k < 0 и поэтому система управления всегда устойчива. Предположим теперь, что . Тогда . Характеристическое уравнение p2 + + k = 0. Поэтому p1,2=. Система находится на границе устойчивости. В ней существуют незатухающие колебания.

Анализ устойчивости с помощью частотных критериев

Основным недостатком рассмотренного алгебраического подхода к анализу устойчивости является то, что в сложных системах управления трудно установить связь между корнями знаменателя рk , k=1, 2, …, n, и параметрами элементарных звеньев, составляющих систему управления. Это приводит к трудностям коррекции неустойчивых систем. Для того, чтобы упростить анализ устойчивости, желательно проводить этот анализ по передаточной функции H(p) разомкнутой системы управления.

В 1932 г. американский ученый Найквист разработал эффективный метод анализа устойчивости усилителей с обратной связью. В 1938 г. советский ученый А.В. Михайлов обобщил метод Найквиста на замкнутые системы автоматического управления.

Критерий Найквиста основан на построении годографа передаточной функции H(jw) разомкнутой системы управления. Годографом передаточной функции H(j w ) называется кривая, прочерчиваемая концом вектора H(jw) =|H(jw)|ejj(w) на комплексной плоскости при измерении частоты w от 0 до бесконечности.

Наиболее просто формулируется критерий устойчивости Найквиста: замкнутая система управления устойчива, если годограф передаточной функции H(jw) разомкнутой системы не охватывает на комплексной плоскости точку c координатами (-1, j0). На рисунках показаны примеры годографов устойчивой (рис. 16,а) и неустойчивой (рис. 16,б) систем управления.

Если годограф проходит через точку -1, то говорят, что система находится на границе устойчивости. В этом случае на некоторой частоте H(jw0)= -1 и в системе могут существовать незатухающие колебания частоты w0. В неустойчивых системах уровень сигнала x(t) будет нарастать со временем. В устойчивых - уменьшаться.

Запас устойчивости

Еще одним достоинством рассматриваемого критерия является возможность определения запаса устойчивости системы управления. Запас устойчивости характеризуют двумя показателями: запасом устойчивости по усилению и запасом устойчивости по фазе .

Запас устойчивости по усилению определяется величиной g =1/|H(jw0)|, где w0 - частота, на которой (рис. 17,а). Запас устойчивости g показывает, во сколько раз должен измениться (увеличиться) модуль передаточной функции разомкнутой системы управления, чтобы замкнутая система оказалась на границе устойчивости. Требуемый запас устойчивости зависит от того, насколько в процессе работы может возрастать коэффициент передачи системы по сравнению с расчетным.

Запас устойчивости по фазе оценивается величиной угла , где частота wсp , называемая частотой среза , определяется условием |H(jwcp)|=1 (рис. 17, б).

Величина Dj показывает, насколько должна измениться фазовая характеристика разомкнутой системы управления, чтобы замкнутая система оказалась на границе устойчивости. Запас устойчивости по фазе обычно считается достаточным, если
|Dj| ³ 30o.

Анализ устойчивости с помощью логарифмических амплитудно-частотных характеристик

Во многих случаях разомкнутую систему управления можно представить в виде последовательного соединения n типовых звеньев с передаточными функциями . При этом передаточная функция разомкнутой системы определяется произведением . Логарифмическая амплитудно-частотная характеристика будет равна сумме ЛАХ отдельных звеньев:

.

Поскольку ЛАХ многих элементарных звеньев могут быть аппроксимированы отрезками прямых линий, то ЛАХ разомкнутой системы управления также будет представлена в виде отрезков прямых линий, имеющих наклоны к оси частот, кратные 20 децибелам на декаду.

Пример. Пусть передаточная функция разомкнутой системы имеет следующий вид

.

Такая система содержит два интегратора, форсирующее звено с передаточной функцией и апериодическое звено с передаточной функцией . Представим ЛАХ отдельных звеньев такой системы в виде графиков на рис. 18, а. Суммируя представленные графики, получим ЛАХ разомкнутой системы (рис. 18, б).

Как следует из приведенных рисунков, построение суммарной ЛАХ осуществляется достаточно просто. Необходимо лишь учитывать изменение наклона ЛАХ в точках и , соответствующих сопрягающим частотам форсирующего и апериодического звеньев.

Для проверки условий устойчивости замкнутой системы автоматического управления необходимо в таком же логарифмическом масштабе по оси частот построить фазочастотную характеристику . Однако опыт инженерных расчетов показывает, что замкнутая САУ, как правило, устойчива и обладает запасом устойчивости, если ЛАХ разомкнутой системы вблизи часто-

ты среза имеет наклон –20 дБ/дек. При этом запас устойчивости тем больше, чем больше протяженность этого участка ЛАХ. Обычно считают, что, протяженность участка с наклоном - 20 дБ/дек должна составлять не менее 1 декады. Существуют устойчивые САУ с наклоном ЛАХ большим, чем - 20 дБ/дек, но для таких систем, как правило, очень мал запас устойчивости.

Предположим, что исследуемая САУ имеет наклон около частоты среза больший, чем - 20 дБ/дек (рис. 19)

Учитывая, что при последовательном соединении звеньев САУ их ЛАХ суммируются, нужно включить в САУ такое звено, которое обеспечит устойчивость системы. В рассматриваемом случае таким звеном может быть звено с ЛАХ, показанной на рис. 20.

Действительно, после суммирования ЛАХ системы управления (рис. 19) и дополнительного звена получим ЛАХ, имеющую постоянный наклон - 20 дБ/дек на всех частотах, в том числе и на

частоте среза. В рассматриваемом примере передаточная функция дополнительного корректирующего звена Hф(jw) =1+jwTф, причем w1 = 1/Tф. Введение дополнительных звеньев для обеспечения устойчивости систем управления называется коррекцией САУ, а сами звенья – корректирующими.

В этом разделе были рассмотрены методы исследования одного из важнейших показателей качества систем управления - устойчивости линейных систем. Применение этих методов для анализа конкретных систем обычно осуществляется следующим образом. Вначале строят ЛАХ разомкнутой системы управления. Если система неустойчива, то подбирают и вводят в нее корректирующие звенья таким образом, чтобы наклон ЛАХ на частоте среза составлял - 20 дБ/дек и обеспечивался необходимый запас устойчивости. После этого обязательно исследуют устойчивость скорректированной системы с помощью критерия Найквиста-Михайлова и определяют точные значения запасов устойчивости по усилению и по фазе. При необходимости после этого изменяются параметры системы управления для обеспечения заданного запаса устойчивости.

10.1. Понятие структурной устойчивости. АФЧХ астатических САУ

САУ может быть неустойчивой по двум причинам: неподходящий состав динамических звеньев и неподходящие значения параметров звеньев.

САУ, неустойчивые по первой причине называются структурно неустойчивыми . Это означает, что изменением параметров САУ нельзя добиться ее устойчивости, нужно менять ее структуру.

Например, если САУ состоит из любого количества инерционных и колебательных звеньев, она имеет вид, показанный на рис.72. При увеличении коэффициента усиления САУ K каждая точка ее АФЧХ удаляется от начала координат, пока при некотором значении K крит АФЧХ не пересечет точку (-1, j0 ). При дальнейшем увеличении K , САУ будет неустойчива. И наоборот, при уменьшении K такую САУ в принципе возможно сделать устойчивой, поэтому ее называют структурно устойчивой .

Если САУ астатическая, то при ее размыкании характеристическое уравнение можно представить в виде: pD 1 p(p) = 0 , где n - порядок астатизма , равный количеству последовательно включенных интеграторов. Это уравнение имеет нулевые корни, поэтому при 0 , АФЧХ стремится к (рис.71в и 71г). Например, пусть W р (p) = , здесь = 1 , тогда АФЧХ разомкнутой САУ:

W(j) = = P() + jQ().

Так как порядок знаменателя больше порядка числителя, то при 0 имеем P() - , Q() -j . Подобная АФЧХ представлена на рис.73.

Так как АФЧХ терпит разрыв, трудно сказать, охватывает ли она точку (-1,j0) . В этом случае пользуются следующим приемом: если АФЧХ терпит разрыв, уходя в бесконечность при 0 , ее дополняют мысленно полуокружностью бесконечного радиуса, начинающейся на положительной вещественной полуоси и продолжающейся до АФЧХ в отрицательном направлении. После этого можно применить критерий Найквиста. Как видно из рисунка, САУ, имеющая одно интегрирующее звено, является структурно устойчивой.

Если САУ имеет два интегрирующих звена (порядок астатизма = 2 ), ее АФЧХ уходит в бесконечность во втором квадранте (рис.74). Например, пусть W р (p) = , тогда АФЧХ САУ:

W(j) = = P() + jQ().

При 0 имеем P() -, Q() + j. Такая САУ не будет устойчива ни при каких значениях параметров, то есть она структурно неустойчива.

Структурно неустойчивую САУ можно сделать устойчивой, включив в нее корректирующие звенья (например, дифференцирующие или форсирующие) или изменив структуру САУ, например, с помощью местных обратных связей.

10.2. Понятие запаса устойчивости

В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости .

Запас устойчивости по модулю характеризует удаление годографа АФЧХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием h от критической точки до точки пересечения годографом оси абсцисс (рис.75).

Запас устойчивости по фазе характеризует удаление годографа от критической точки по дуге окружности единичного радиуса и определяется углом между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.

Как уже отмечалось, с ростом коэффициента передачи разомкнутой САУ растет модуль каждой точки АФЧХ и при некотором значении K = K кр АФЧХ пройдет через критическую точку (рис.76) и попадет на границу устойчивости, а при K > K кр замкнутая САУ станет неустойчива. Однако в случае “клювообразных” АФЧХ (получаются из-за наличия внутренних обратных связей) не только увеличение, но и уменьшение K может привести к потере устойчивости замкнутых САУ (рис.77). В этом случае запас устойчивости определяется двумя отрезками h 1 и h 2 , заключенными между критической точкой и АФЧХ.

Обычно при создании САУ задаются требуемыми запасами устойчивости h и , за пределы которых она выходить не должна. Эти пределы выставляются в виде сектора, вычерчиваемого вокруг критической точки, в который АФЧХ разомкнутой САУ входить не должна (рис.78).

10.3. Анализ устойчивости по ЛЧХ

Оценку устойчивости по критерию Найквиста удобнее производить по ЛЧХ разомкнутой САУ. Очевидно, что каждой точке АФЧХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.

Пусть известны частотные характеристики двух разомкнутых САУ (1 и 2), отличающихся друг от друга только коэффициентом передачи K 1 2 . Пусть первая САУ устойчива в замкнутом состоянии, вторая нет.(рис.79).

Если W 1 (p) - передаточная функция первой САУ, то передаточная функция второй САУ W 2 (p) = KW 1 (p) , где K = K 2 /K 1 . Вторую САУ можно представить последовательной цепочкой из двух звеньев с передаточными функциями K (безынерционное звено) и W 1 (p) , поэтому результирующие ЛЧХ строятся как сумма ЛЧХ каждого из звеньев.

Поэтому ЛАЧХ второй САУ: L 2 () = 20lgK + L 1 () ,

а ЛФЧХ: 2 () = 1 () .

Пересечениям АФЧХ вещественной оси соответствует значение фазы = - . Это соответствует точке пересечения ЛФЧХ = - линии координатной сетки. При этом, как видно на АФЧХ, амплитуды A 1 () 2 () > 1 , что соответствует на САЧХ значениям L 1 () = 20lgA 1 () 2 () > 0 .

Сравнивая АФЧХ и ЛФЧХ можно заключить, что система в замкнутом состоянии будет устойчива, если значению ЛФЧХ = - будут соответствовать отрицательные значения ЛАЧХ и наоборот. Запасам устойчивости по модулю h 1 и h 2 , определенным по АФЧХ соответствуют расстояния от оси абсцисс до ЛАЧХ в точках, где = - , но в логарифмическом масштабе.

Особыми точками являются точки пересечения АФЧХ с единичной окружностью. Частоты c1 и c2 , при которых это происходит называют частотами среза .

В точках пересечения A() = 1 = > L() = 0 - ЛАЧХ пересекает горизонтальную ось. Если при частоте среза фаза АФЧХ c1 > - (рис.79а кривая 1), то замкнутая САУ устойчива. На рис.79б это выглядит так, что пересечению ЛАЧХ горизонтальной оси соответствует точка ЛФЧХ, расположенная выше линии = - . И наоборот для неустойчивой замкнутой САУ (рис.79а кривая 2) c2 -, поэтому при = c2 ЛФЧХ проходит ниже линии = - . Угол 1 = c1 -(-) является запасом устойчивости по фазе. Этот угол соответствует расстоянию от линии = - до ЛФЧХ.

В каком квадранте уходит в бесконечность АФЧХ разомкнутой САУ если порядок астатизма равен трем? Является ли такая САУ структурно устойчивой в замкнутом состоянии:

Как сделать устойчивой структурно неустойчивую САУ?

Что называется запасом устойчивости по модулю?

Что называется запасом устойчивости по фазе?

В чем особенность определения запасов устойчивости для клювообразных САУ?

Как влияет коэффициент усиления САУ на запасы устойчивости?

Чему соответствуют на АФЧХ пересечение ЛАЧХ оси w?

Чему соответствуют на АФЧХ пересечение ЛФЧХ значения j = -p?

Что называется частотой среза?

Сформулируйте критерий Найквиста для логарифмических характеристик.

В чем особенность логарифмических характеристик, если АФЧХ имеет клювообразный характер?

PAGE \* MERGEFORMAT 14

Лекция №4

Устойчивость САУ

Свойство системы приходить в исходное состояние после снятия возмущения называется устойчивостью.

Определение.

Кривые 1 и 2 характеризуют устойчивую систему, кривые 3 и 4 характеризуют системы неустойчивые.ε

Системы 5 и 6 на границе устойчивости  5 - нейтральная система, 6 - колебательная граница устойчивости.

Пусть дифференциальное уравнение САУ в операторной форме имеет вид 

Тогда решение дифференциального уравнения (движение системы) состоит из двух частей  Вынужденное движение того же вида что и входное воздействие.

При отсутствии кратных корней где С i -постоянные интегрирования, определяемые из начальных условий,

 1 ,  2 …,  n – корни характеристического уравнения

Расположение корней характеристического

уравнения системы на комплексной плоскости

Корни характеристического уравнения не зависят ни от вида возмущения, ни от

начальных условий, а определяются только коэффициентами а 0 , а 1 , а 2 ,…,а n , то есть параметрами и структурой системы.

1-корень действительный, больше нуля;

2-корень действительный, меньше нуля;

3-корень равен нулю;

4-два нулевых корня;

5-два комплексных сопряженных корня, действительная часть которых

Положительна;

6-два комплексных сопряженных корня, действительная часть которых отрицательная;

7-два мнимых сопряженных корня.

Методы анализа устойчивости :

1. Прямые (основаны на решении дифференциальных уравнений);
2. Косвенные (критерии устойчивости).

Теоремы А.М. Ляпунова.

Теорема 1.

Теорема 2.

Примечания:

1. Если среди корней характеристического уравнения имеется два и более нулевых корня, то система неустойчива.
2. Если один корень нулевой, а все остальные находятся в левой полуплоскости, то система нейтральна.
3. Если 2 корня мнимые сопряженные, а все остальные в левой полуплоскости, то система на колебательной границе устойчивости.

Критерии устойчивости САУ.

Критерий устойчивости - это правило, позволяющее выяснить устойчивость системы без вычисления корней характеристического уравнения.

В 1877г. Раус установил:

1. Критерий устойчивости Гурвица

Критерий разработан в 1895г.

Пусть определено характеристическое уравнение замкнутой системы: уравнение приводим к виду, чтобы a 0 >0.

Составим главный определитель Гурвица по следующему правилу:

по главной диагонали записываются коэффициенты уравнения, начиная со второго по последний, столбцы вверх от диагонали заполняются коэффициентами с возрастающими индексами, а столбцы вниз от диагонали - коэффициентами с убывающими индексами. В случае отсутствия в уравнении какого-либо коэффициента и вместо коэффициентов с индексами меньше 0 и больше n пишут нуль.

Выделим диагональные миноры или простейшие определители в главном определителе Гурвица:

Формулировка критерия.

Для систем выше второго порядка кроме положительности всех коэффициентов характеристического уравнения необходимо выполнение следующих неравенств:

1. Для систем третьего порядка:
2. Для систем четвертого порядка:
3. Для систем пятого порядка:

1. Для систем шестого порядка:

Пример. Дано характеристическое уравнение исследовать устойчивость системы по Гурвицу.

Для устойчивых систем необходимо и

2. Критерий Рауса

Критерий Рауса используется при исследовании устойчивости систем высокого порядка.

Формулировка критерия:

Таблица Рауса.

Алгоритм заполнения таблицы: в первой и второй строках записываются коэффициенты уравнения с четными и нечетными индексами; элементы остальных строк вычисляются по следующему правилу:

Достоинство критерия: можно исследовать устойчивость систем любого порядка.

2. Критерий устойчивости Найквиста

Принцип аргумента

В основе частотных методов лежит принцип аргумента.

Проведем анализ свойств многочлена вида:

Где  i - корни уравнения

На комплексной плоскости каждому корню соответствует вполне определенная точка. Геометрически каждый корень  i можно изобразить в виде вектора, проведенного из начала координат в точку  i : |  i | - длина вектора, arg  i - угол между вектором и положительным направлением оси абсцисс. Отобразим D(p) в пространство Фурье, тогда где j  -  i - элементарный вектор.

Концы элементарных векторов находятся на мнимой оси.

Модуль вектора, а аргумент (фаза)

Направление вращения вектора против часовой стрелки принимают за ПОЛОЖИТЕЛЬНОЕ. Тогда при изменении  от до каждый элементарный вектор ( j  -  i ) повернется на угол +  , если  i лежит в левой полуплоскости.

Пусть D ( )=0 имеет m корней в правой полуплоскости и n - m корней в левой, тогда при возрастании  от до изменение аргумента вектора D(j  ) (угол поворота D(j  ), равный сумме изменений аргументов элементарных векторов) будет

Принцип аргумента:

Критерий Найквиста базируется на частотных характеристиках разомкнутой цепи САУ, так как по виду частотных характеристик разомкнутой цепи можно судить об устойчивости замкнутой системы.

Критерий Найквиста нашел широкое применение в инженерной практике по следующим причинам:

1. Устойчивость системы в замкнутом состоянии исследуют по частотной передаточной функции ее разомкнутой цепи, а эта функция, чаще всего состоит из простых сомножителей. Коэффициентами являются реальные параметры системы, что позволяет выбирать их из условий устойчивости.
2. Для исследования устойчивости можно использовать экспериментально полученные частотные характеристики наиболее сложных элементов системы (объект регулирования, исполнительный орган), что повышает точность полученных результатов.
3. Исследовать устойчивость можно по ЛЧХ, построение которых несложно.
4. Удобно определять запасы устойчивости.

1. Система, устойчивая в разомкнутом состоянии

Пусть введем вспомогательную функцию заменим p  j  , тогда

Согласно принципа аргумента изменение аргумента D(j  ) и D з (j  ) при 0<  <  равно Тогда то есть годограф W 1 (j  ) не должен охватывать начало координат.

Для упрощения анализа и расчетов сместим начало радиуса-вектора из начала координат в точку (-1, j 0), а вместо вспомогательной функции W 1 (j  ) используем АФХ разомкнутой системы W (j  ).

Формулировка критерия №1

Примеры.

Отметим, что разность числа положительных и отрицательных переходов АФХ левее точки (-1, j 0) равна нулю.

2. Система, имеющая полюсы на мнимой оси в разомкнутом состоянии

Для анализа устойчивости системы АФХ дополняют окружностью бесконечно большого радиуса при  0 против часовой стрелки до положительной вещественной полуоси при нулевых полюсах, а в случае чисто мнимых корней - полуокружностью по часовой стрелке в точке разрыва непрерывности АФХ.

Формулировка критерия №2

1. Система с неустойчивой разомкнутой цепью

Более общий случай - знаменатель передаточной функции разомкнутой системы содержит корни, лежащие в правой полуплоскости. Появление неустойчивости разомкнутой системы вызывается двумя причинами:

1. Следствием наличия неустойчивых звеньев;
2. Следствием потери устойчивости звеньев, охваченных положительной или отрицательной обратными связями.

X отя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным и его надо избегать, стремясь использовать только устойчивые местные обратные связи. Это объясняется наличием нежелательных свойств, в частности появлением условной устойчивости, которая при имеющихся обычно в системе нелинейностях может в некоторых режимах привести к потере устойчивости и появлению автоколебаний. Поэтому, как правило, при расчете системы выбирают такие местные обратные связи, которые были бы устойчивыми при разомкнутой главной обратной связи .

Пусть характеристический многочлен D (p ) разомкнутой системы имеет m корней с положительной вещественной частью.

Тогда

Вспомогательная функция при замене p  j  согласно принципа аргумента для устойчивых замкнутых систем должна иметь следующее изменение аргумента при

Формулировка критерия №3

Формулировка Я.З. Цыпкина

Критерий Найквиста для ЛЧХ

Примечание: фазовая характеристика ЛЧХ астатических систем дополняется монотонным участком +  /2 при  0.

Пример 1. Здесь m =0  система устойчива, но при уменьшении k система может быть неустойчива, поэтому такие системы называются условно-устойчивыми.

Пример 2. 20 lgk 1/ T 0 Здесь При любых k система неустойчива. Такие системы называются структурно-неустойчивыми.

Пример 3. АФХ охватывает точку с координатами (-1, j 0) 1/2 раза, следовательно замкнутая система устойчива.

Пример 4. при  0 АФХ имеет разрыв, и поэтому ее нужно дополнить дугой бесконечно большого радиуса от отрицательной вещественной полуоси. На участке от -1 до -  имеется один положительный переход и полтора отрицательных. Разность между положительными и отрицательными переходами равна -1/2, а для устойчивости замкнутой системы требуется +1/2, так как характеристический полином разомкнутой системы имеет один положительный корень - система неустойчива.

Абсолютно-устойчивой называют систему, которая сохраняет устойчивость при любом уменьшении коэффициента усиления разомкнутой цепи, иначе система условно- устойчивая.

Системы, которые можно сделать устойчивыми путём изменения их параметров, называются структурно-устойчивыми , иначе – структурно-неустойчивыми.

Запасы устойчивости

Для нормального функционирования всякая САР должна быть удалена от границы устойчивости и иметь достаточный запас устойчивости. Необходимость этого обусловлена следующими причинами:

1. Уравнения элементов САР, как правило, идеализированы, при их составлении не учитывают второстепенные факторы;
2. При линеаризации уравнений погрешности приближения дополнительно увеличиваются;
3. Параметры элементов определяют с некоторой погрешностью;
4. Параметры однотипных элементов имеют технологический разброс;
5. При эксплуатации параметры элементов изменяются вследствие старения.

В практике инженерных расчетов наиболее широко используют определение запаса устойчивости на основе критерия НАЙКВИСТА, по удалению АФХ разомкнутой системы от критической точки с координатами (-1, j 0), что оценивают двумя показателями: запасом устойчивости по фазе  и запасом устойчивости по модулю (по амплитуде) H .

Для того чтобы САР имела запасы устойчивости не менее  и H , АФХ ее разомкнутой цепи при удовлетворении критерия устойчивости не должна заходить в часть кольца, заштрихованного на рис. 1, где H определяется соотношением

Если устойчивость определяется по ЛЧХ условно-устойчивых систем, то для обеспечения запасов устойчивости не менее  и h необходимо, чтобы:

а) при h  L  - h фазо-частотная характеристика удовлетворяла неравенствам θ > -180  +  или θ < -180  -  , т.е. не заходила в заштрихованную область 1 на рис. 2;

б) при -180  +   θ  -180  -  амплитудно-частотная характеристика удовлетворяла неравенствам L < - h или L > h , т.е. не заходила в заштрихованные области 2" и 2"" на рис. 2.

Для абсолютно устойчивой системы запасы устойчивости  и h определяют так, как показано на рис. 3:

1. Запас по фазе

1. Запас по модулю h =- L (ω -π ), где ω -π – частота, при которой θ=-180 ˚ .

Необходимые значения запасов устойчивости зависит от класса САР и требований к качеству регулирования. Ориентировочно должно быть  =30  60  и h =6  20дБ.

Минимально допустимые запасы устойчивости по амплитуде должны быть не менее 6дБ (то есть передаточный коэффициент разомкнутой системы в два раза меньше критического), а по фазе не менее 25  30  .

Устойчивость системы со звеном чистого запаздывания

Если АФХ разомкнутой системы проходит через точку (-1, j 0), то система на грани устойчивости.

Систему с чистым запаздыванием можно сделать устойчивой, если в схему включить безынерционное звено с передаточным коэффициентом, меньшим 1. Возможны и другие виды корректирующих устройств.

Структурно-устойчивые и структурно-неустойчивые системы

Один из способов изменения качества системы (в смысле устойчивости) – это изменить передаточный коэффициент разомкнутой системы.

При изменении k L ( ) поднимется либо опускается. Если k увеличивать, L ( ) поднимается и  ср будет возрастать, а система останется неустойчивой. Если k уменьшать, то систему можно сделать устойчивой. Это один из способов коррекции системы.

Системы, которые можно сделать устойчивыми путем изменения параметров системы, называются СТРУКТУРНО-УСТОЙЧИВЫМИ.

Для этих систем есть критический передаточный коэффициент разомкнутой системы. K крит. – это такой передаточный коэффициент, когда система на грани устойчивости.

Существуют системы СТРУКТУРНО-НЕУСТОЙЧИВЫЕ – это такие системы, которые невозможно сделать устойчивыми изменением параметров системы, а требуется для устойчивости изменять структуру системы.

Пример.

Рассмотрим три случая:

1. Пусть

Тогда

Проверим работу системы на устойчивость.

Δ = а 3 Δ 2 >0.

Для определения k рс.кр. приравняем нулю  2 .

Тогда

При при

Рассматриваемая система СТРУКТУРНО-УСТОЙЧИВАЯ, так как ее можно стабилизировать путем изменения параметров звеньев.

1. Пусть и те же, что в первом случае.

Теперь Статической ошибки по каналу управления нет.

Условия устойчивости по Гурвицу:

Пусть  2 =0, тогда если то система неустойчивая.

Данная система с астатизмом 1-го порядка СТРУКТУРНО-УСТОЙЧИВАЯ.

1. Пусть

Всегда система неустойчива. Эта система СТРУКТУРНО-НЕУСТОЙЧИВАЯ.

Устойчивость САУ, общие понятия устойчивости

Наименование параметра	Значение
Тема статьи:	Устойчивость САУ, общие понятия устойчивости
Рубрика (тематическая категория)	Математика

Устойчивость системы автоматического управления является одной из важнейших характеристик системы, т.к. от нее зависит работоспособность системы. Система, у которой отсутствует устойчивость, не может качественно решать задачу управления. Отсутствие устойчивости также может привести к разрушению самой системы в процессе управления или разрушению объекта управления, в связи с этим использование неустойчивых систем нецелœесообразно.

Устойчивость системы автоматического управления - это свойство системы воз-

вращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему состояния первоначального равновесия.

Примером устойчивых и неустойчивых систем могут служить системы из шарика, расположенного на вогнутой и выпуклой поверхности, представленные на рисунке 60.

Рис.60. Примеры систем: а) устойчивой; б) неустойчивой

На рисунке 60а шарик, расположенный на вогнутой поверхности и смещенный в сторону определœенным усилием, после окончания внешнего воздействия возвратится в положение первоначального равновесия. При отсутствии трения о поверхность или его минимальном значении шарик будет совершать непродолжительные колебания около положения равновесия до возвращения в первоначальное положение равновесия (кривая 1- затухающий колебательный процесс). При большом трении шарик возвратится в положение первоначального равновесия без колебаний (кривая 2 - апериодический процесс). При очень большом значении трения шарик может не вернуться в положение первоначального равновесия (кривая 3), но возвратится в область, близкую к положению равновесия. В рассмотренном случае налицо наличие устойчивой системы. В устойчивых САУ возникают подобные переходные процессы (затухающие колебательные и апериодические).

На рисунке 60б шарик, расположенный на выпуклой поверхности и смещенный в сторону определœенным усилием, не возвратится в положение первоначального равновесия (кривая 4), в связи с этим система является неустойчивой. В неустойчивых системах возникают переходные процессы виде расходящихся колебаний (кривая 5) или апериодические (кривая 4).

Неустойчивость САУ, как правило, возникает из-за очень сильного действия обратной связи. Причинами динамической неустойчивости обычно являются значительные инœерционные характеристики звеньев замкнутой системы, из-за которых сигнал обратной связи в режиме колебаний так отстает от входного сигнала, что оказывается с ним в фазе. Получается, что характер действия отрицательной обратной связи приобретает характер

положительной.

Составим математическое описание устойчивости и неустойчивости. Так как устойчивость системы зависит только от характера ее свободного движения, то данное свободное движение системы можно описать однородным дифференциальным уравнением:

характеристическое уравнение, которого будет представлено следующим выражением:

Общее решение однородного дифференциального уравнения (2.19.) представим в следующем виде:

где C k – постоянные, зависящие от начальных условий, p k – корни характеристического уравнения.

Корни характеристического уравнения бывают комплексными (p k = α k ± jβ k ), действительными (p k = α k ) или мнимыми (p k = jβ k ). Комплексные корни всœегда попарно сопряжены между собой, ᴛ.ᴇ. если имеется корень уравнения с положительной мнимой частью, то обязательно будет существовать корень с такой же по модулю, но отрицательной мнимой частью. y(t) при t → ∞ из (2.21.) будет стремиться к нулю лишь тогда, когда каждое слагаемое С к е p k t → 0. Характер данной функции будет зависеть от вида корня. Возможные случаи расположения корней p k на комплексной плоскости и соответствующие им функции y(t) = С к е p k t представлены на рисунке 61. Вид функций показан внутри эллипсов.

Рис.61. Влияние расположения корней характеристического уравнения на

составляющие свободного движения системы

На рисунке 61 видно, что если каждому действительному корню p k = α k для выражения (2.21.) будет соответствовать слагаемое:

y к (t) = С к е α k t (2.22.)

тогда приα к < 0 (корень p 1) функция при t → ∞ будет стремиться к нулю, при α к > 0 (корень p 3 ) функция будет неограниченно возрастать, а при α к = 0 (корень p 2)функция будет оставаться постоянной.

В случае если характеристическое уравнение будет иметь комплексные корни, то каждой паре сопряженных комплексных корней p k, k+1 = α k ± jβ k , будут соответствовать два слагаемых, которые можно объединить и представить в виде следующего выражения:

Данная функция представляет собой синусоиду с изменяющейся по экспоненте амплитудой и частотой β k . При отрицательной действительной части двух комплексных корней α к, к+1 < 0 , (корни p 4 и p 5 )колебательная составляющая функции будет затухать, а при положительной действительной части α к, к+1 > 0 , (корни p 8 и p 9 ) амплитуда колебаний будет увеличиваться неограниченно. При отсутствии действительной части комплексных корней α к, к+1 = 0 (корни p 6 и p 7 ), ᴛ.ᴇ. наличии только мнимых корней, функция будет представлять собой незатухающую синусоиду с частотой β k .

Исходя из определœения устойчивости, в случае если первоначальное положение равновесия принимается за ноль, то у устойчивых систем величина выходного параметра с течением времени должна стремиться к нулю, ᴛ.ᴇ. система сама возвратится в положение равновесия. Необходимым и достаточным условием этого является, чтобы всœе слагаемые решения дифференциального уравнения (2.21.) с течением времени стремились к нулю, что должна быть достигнуто при отрицательных действительных корнях уравнения, а комплексные корни должны иметь отрицательную действительную часть. Существование хотя бы одного положительного действительного корня или пары комплексных корней с положительной действительной частью приведет к тому, что величина выходного параметра системы не возвратится к первоначальному значению, ᴛ.ᴇ. система будет неустойчивой.

Анализируя местоположение корней характеристического уравнения на комплексной плоскости, представленное на рисунке 62, можно заметить, что САУ является устойчивой, в случае если всœе корни характеристического уравнения находятся в левой полуплоскости и всœе они являются действительными отрицательными или комплексными с отрицательной действительной частью. Наличие хотя бы одного корня в правой полуплоскости будет характеризовать неустойчивость системы.

Устойчивость системы является внутренним свойством системы, зависящим только от вида корней характеристического уравнения, описывающего свойства системы, и не зависящим от внешнего воздействия. Необходимым и достаточным условием устойчивости системы является положение всœех корней уравнения в левой (отрицательной) полуплоскости.

Положительную и отрицательную полуплоскости, в которых находятся положительные или отрицательные корни характеристического уравнения, обеспечивающие устойчивость или неустойчивость системы, разделяет мнимая ось ± jβ . Данная ось является границей устойчивости, в связи с этим если у характеристического уравнения есть одна пара чисто мнимых корней p k, k+1 =± jβ k , а другие корни находятсяв отрицательной полуплоскости, то система характеризуется наличием незатухающих колебаний с частотой ω = β к. Принято считать, что в таком случае система находится на колебательной границе устойчивости .

Точка β = 0 на мнимой оси соответствует нулевому корню. Считается, что уравнение, имеющее один нулевой корень, находится на апериодической границе устойчивости , а при наличии двух нулевых корней система неустойчива.

Рис.62. Расположение корней характеристического уравнения устойчивой системы на

комплексной плоскости

Не стоит забывать, что уравнения почти всœех реальных САУ не являются линœейными, а приведены к линœейным уравнениям с помощью линœеаризации, в связи с этим допущения, сделанные при линœеаризации, могут повлиять на правильность определœения устойчивости системы.

А. М. Ляпунов в 1892 ᴦ. в своей работе ʼʼОбщая задача об устойчивости движенияʼʼ привел доказательство теоремы, в которой были сделаны следующие выводы для линœеаризованных уравнений:

1. В случае если всœе действительные корни характеристического уравнения системы являются отрицательными, то система считается устойчивой.

2. В случае если хотя бы один действительный корень характеристического уравнения системы положительный, то система считается неустойчивой.

3. В случае если характеристическое уравнение линœеаризованной системы имеет хотя бы один нулевой корень или одну пару мнимых корней, то нельзя судить об устойчивости реальной системы по линœеаризованному уравнению.

Следовательно, вывод об устойчивости реальных систем крайне важно делать на базе анализа исходного нелинœейного уравнения и для определœения неустойчивости или устойчивости системы будет достаточно выявить положительность (отрицательность) действительных корней характеристического уравнения.

Критериями устойчивости называют определœенные правила, по которым в теории автоматического управления определяют знаки корней характеристического уравнения, не решая его. Различают алгебраические и частотные критерии устойчивости.

Алгебраическими критериями устойчивости системыназывают крайне важно е и достаточное условие отрицательности корней при определœенных значениях коэффициентов в характеристическом уравнении.

Частотными критериями устойчивости системы установлена зависимость устойчивости системы от формы частотных характеристик системы.

Устойчивость САУ, общие понятия устойчивости - понятие и виды. Классификация и особенности категории "Устойчивость САУ, общие понятия устойчивости" 2017, 2018.