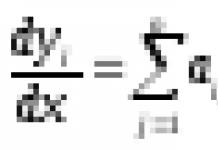Обозначим через J момент инерции маятника относительно оси О. Пусть точка С является центром масс. Силу тяжести можно разложить на две составляющие, одна из которых уравновешивается реакцией оси. Маятник приходит в движение под действием другой составляющей , величина, которой:

Для малых углов sin a » a и выражение (1) запишем:

Знак минус означает, что сила направлена в сторону, противоположную отклонению маятника от положения равновесия.

Основное уравнение динамики вращательного движения для физического маятника запишется:

Момент силы относительно оси О с учетом (2):

где l – расстояние от центра масс С до оси О.

Угловое ускорение маятника:

Поставив (4) и (5) в уравнение (3), получим:

откуда

Обозначив

получим:

По структуре уравнение (6) является дифференциальным уравнением гармонических колебаний с циклической частотой w . Период колебаний физического маятника равен:

Отсюда момент инерции физического маятника:

Величина

называется приведенной длиной физического маятника, равной длине математического маятника, имеющего тот же период колебаний, что и физический, т.е.

Точка О 1 , лежащая на прямой, проведенной через точку подвеса О и центр масс С, на расстоянии приведенной длины l 0 от оси вращения, называется центром качания маятника (рис.1). Центр качания лежит всегда ниже центра масс. Точка подвеса О и центр качания О 1 сопряжены друг с другом, т.е. перенос точки подвеса в центр качания не меняет периода колебания маятника. Точка подвеса и центр качания обратимы, а расстояние между этими точками представляет собой приведенную длину l 0 одного из типов физического маятника, так называемого оборотного маятника.

Обозначим через J 0 момент инерции маятника относительно оси, проходящей через его центр масс. На основании теоремы Штейнера момент инерции J относительно любой оси, параллельной первой:

где m – масса маятника, l – расстояние между осями.

Тогда при подвешивании маятника за точку подвеса О период колебаний:

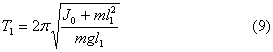
а при подвешивании за центр качания О 1 , когда маятник находится в перевернутом положении, период:

где l 2 и l 1 – расстояние между центром масс и соответствующими осями колебаний.

Из уравнений (9) и (10):

откуда:

Формула (11) остается справедливой при колебаниях маятника относительно двух произвольных осей О и О / , не обязательно сопряженных, но расположенных по разные стороны от центра масс маятника.

Описание рабочей установки и метода измерений.

Для определения ускорения свободного падения применяется прибор ФП-1 (рис.2),

состоящий из настенного кронштейна 1, на котором смонтированы подушки 2 опорных призм и физического маятника представляющего собой однородный металлический стержень 11, на котором крепятся чечевицы 5 и 9. Чечевица 9 закреплена жестко и является неподвижной. Чечевица 5, находящаяся на конце стержня, может перемещаться по шкале 3 с нониусом 4 и фиксируется в нужном положении винтом 6. Маятник можно подвешивать на опорные призмы 7 и 10. В комплект прибора входит специальная подставка для определения положения центра масс маятника. Перемещением чечевицы 5 можно добиться равенства периодов колебаний маятника при подвесе его на опорные призмы 7 и 10, и тогда оси колебаний становятся сопряженными, расстояние между опорными призмами становится равным приведенной длине физического маятника.

Величина ускорения свободного падения определяется на основе формулы (11). Эксперимент сводится к измерению величин Т 1 , Т 2 , l 1 , l 2 . Формула (8) является исходной для определения момента инерции физического маятника.

Ход работы

1) Определение ускорения свободного падения .

1. Подвесить маятник на опорную призму 7, отклоняют на небольшой угол и измеряют секундомером время t 1 30-50 полных колебаний. Опыт повторяют не менее 5 раз и находят среднее значение времени < t 1 > выбранного числа колебаний.

2. Определяют период колебания:

где n – число колебаний.

3. Для нахождения положения центра масс маятника снять его с подушек опорных призм и балансировать на горизонтальном ребре призмы, укрепленном на столе до тех пор, пока моменты сил тяжести, действующие на правую и левую часть маятника окажутся равными. В случае равновесия центр масс маятника будет расположен в стержне против точки опоры. Не снимая маятник с ребра призмы, линейкой измеряют расстояние l 1 между опорой 7 и центром масс.

4. Перевернув маятник, подвешивают его на опорную призму 10. Выбрать то же число колебаний n и, повторить опыт не менее 5 раз, находят период колебания:

При этом измеренные значения периодов Т 1 и Т 2 должны отличаться не более чем на 5%

5. Найтирасстояние l 2 между ребром опорной призмы 10 и центром масс: l 2 = l 0 – l 1 , где l 0 – расстояние между ребрами опорных призм 7 и 10 (для данного маятника l 0 =0,730м ).

6. Вычисляют среднее значение < g > по формуле (11)

7. Оценивают абсолютную погрешность результата, исходя из табличного значения искомой величины g табл для широты г. Братска. Найти относительную погрешность.

8. Результаты измерений и вычислений заносят в таблицу 1.

Таблица 1

2) Определение момента инерции физического маятника .

1. Найти среднее значение момента инерции физического маятника J относительно оси колебаний по формуле (8). Для колебаний маятника, подвешенного на опору 10, Т =Т 2 и l = l 2 . Масса маятника m = 10,65кг.

2. Методом расчета погрешностей косвенных измерений найти абсолютную погрешность результата D J .

3. Данные результатов измерений и вычислений заносят в таблицу 2.

Таблица 2

Вопросы для допуска к работе

1. Какова цель работы?

2. Что называется физическим маятником? Какой маятник называется оборотным?

3. Запишите формулу периода колебаний физического маятника и поясните физический смысл величин, входящих в нее. При каких условиях справедлива эта формула?

4. Опишите рабочую установку и ход эксперимента.

Вопросы для защиты работы

1. Выведите формулу для периода колебаний физического маятника.

2. Получите дифференциальное уравнение гармонических колебаний физического маятника, приведите его решение.

3. Что называется приведенной длиной физического маятника?

4. Сформулируйте теорему Штейнера.

5. Выведите рабочую формулу:

для определения ускорения свободного падения;

для определения момента инерции физического маятника.

6. Получите дифференциальным методом формулу для расчета относительной погрешности D J / J и укажите пути повышения точности результата эксперимента.

Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции. В положении равновесия центр инерции маятника С находится под точкой подвеса маятника O, на одной с ней вертикали (рис. 50). При отклонении маятника от положения равновесия на угол α возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

М = – mglsin(α)

где m – масса маятника, а l – расстояние между точкой подвеса и центром инерции маятника. Знак «–» означает, что вращательный момент стремится вернуть маятник в положение равновесия, т. е. направлен в сторону, противоположную изменения угла Δα. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой J , можно написать:

Введем обозначение:

Тогда для малых отклонений, когда выполняется условие sin(α) ≈ α, получаем уравнение гармонических колебаний:

При малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, циклическая частота которых определяется формулой (137). Соответственно, период колебаний физического маятника равен:

Физический маятник

Из сопоставления формул (139) и (134) следует, что математический маятник с длиной

будет иметь такой период колебаний, как и данный физический маятник. Величину (140) называют приведенной длиной физического маятника. Таким образом,приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку О" на рис. 50).

По теореме Штейнера момент инерции маятника l может быть представлен в виде

J = J 0 + ml 2 , (141)

где J 0 – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника. Подставив (141) в формулу (140), получаем:

Из (142) следует, что приведенная длина всегда больше l , так что точка подвеса и центр качания лежат по разные стороны от центра инерции.

Подвесим маятник в точке, совпадающей с центром качания О". В соответствии с (142) приведенная длина в этом случае будет равна

где l" – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l" = L – l , выражение (143) можно записать следующим образом:

Поскольку J 0 + ml 2 равно моменту инерции относительно первоначальной оси вращения J , и этой же величине, согласно (140) равно выражение mlL , то числитель дроби будет равен нулю. Поэтому L" = L. Это означает, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

Это положение называется

РОСЖЕЛДОР

Государственное образовательное учреждение

«Ростовский государственный университет путей сообщения»

(РГУПС)

Определение момента инерции физического маятника

Методические указания к лабораторной работе по физике

Ростов-на-Дону

Ладакин, Ю. Н.

Определение момента инерции физического маятника: методические указания к лабораторной работе по физике / , ; Рост. гос. ун-т путей сообщения. – Ростов н/Д, 2007. – 10 с. : ил. – Библиогр.: 2 назв.

Содержатся краткие теоретические сведения по разделам «Колебания» и «Динамика твердого тела». Дано описание и принцип действия лабораторной установки, порядок выполнения работы и рекомендуемая литература. Сформулированы контрольные вопросы для закрепления полученных знаний.

Методические указания одобрены к изданию кафедрой «Физика» РГУПС. Предназначены для студентов всех специальностей РГУПС.

Рецензент д-р физ.-мат. наук, проф. (РГУПС)

Учебное издание

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО МАЯТНИКА

Методические указания к лабораторной работе по физике

Редактор

Техническое редактирование и корректура

Подписано к печати 28.12.07. Формат 60´84/16.

Бумага газетная. Ризография. Усл. печ. л. 0.58.

Уч.-изд. л. 0.53. Тираж 50 экз. Изд. № 58. Заказ №

Ростовский государственный университет путей сообщения.

Ризография РГУПС.

Адрес университета: 344038, г. Ростов н/Д, пл. Ростовского Стрелкового Полка Народного Ополчения, 2.

Ó Ростовский государственный университет путей сообщения, 2007

Приборы и принадлежности: маятник Обербека, испытываемое тело (диск), электронный секундомер, штангенциркуль, линейка, отвертка.

Цель работы: определение момента инерции физического маятника экспериментальным и расчетным способами с использованием теоремы Штейнера.

Момент инерции – это физическая величина, количественно характеризующая инерциальные свойства тела при его вращательном движении . Инерция вращения твердого тела зависит не только собственно от массы тела, но и от распределения этой массы в пространстве относительно оси вращения.

Относительно просто рассчитываются моменты инерции геометрически симметричных тел. Аналитический расчет моментов инерции тел произвольной формы представляет собой громоздкую, требующую опыта вычислений задачу.

Твердое тело произвольной формы, совершающее колебания относительно оси, проходящей через точку подвеса (рис. 1), называется физическим маятником . Требуется определить момент инерции этого маятника.

В положении равновесия центр масс https://pandia.ru/text/80/230/images/image006_43.gif" width="40" height="23">.

На маятник действуют две силы: сила тяжести https://pandia.ru/text/80/230/images/image008_41.gif" width="23" height="27"> (полагаем, что силы трения и сопротивления движению маятника отсутствуют). Отклоним маятник от вертикали на угол (угловое смещение ). Дальнейшее движение предоставленного самому себе маятника можно рассматривать как вращательное относительно оси, совпадающей с осью , перпендикулярной к плоскости рисунка.

Согласно основному закону динамики вращательного движения угловое ускорение маятника () относительно оси равно отношению результирующего момента всех сил, действующих на маятник, к его моменту инерции относительно той же оси:

. (1)

Момент силы , условно показанной на , равен нулю (как видно из рисунка – равно нулю плечо этой силы), и, следовательно, результирующий момент сил равен моменту силы тяжести относительно оси :

, (2)

где: – масса физического маятника, – ускорение свободного падения, https://pandia.ru/text/80/230/images/image003_53.gif" width="20" height="21"> и центром масс . Знак минус в формуле (2) указывает, что момент силы тяжести препятствует увеличению углового смещения .

При малых амплитудах (https://pandia.ru/text/80/230/images/image017_28.gif" width="79" height="27"> и из (1) с учетом (2) приходим к линейному дифференциальному уравнению 2-го порядка:

, где . (3)

Это означает, что малые колебания физического маятника являются гармоническими с круговой частотой и периодом (за период фаза колебаний изменяется на ):

. (4)

С помощью формулы (4) можно экспериментально определять момент инерции любого тела путем измерения величин , и :

. (5)

Физический маятник можно получить с помощью маятника Обербека . Он состоит из крестовины, выполненной из 4-х стержней и прикрепленной к втулке, вращающейся на жестко закрепленной горизонтальной оси. Если на одном из стержней закрепить тело, например диск, то полученная система будет представлять собой физический маятник (рис. 2). Ось вращения полученного маятника совпадает с центром масс маятника Обербека.

Непосредственное использование формулы (5) для расчета момента инерции данного маятника затруднительно. Это обусловлено сложностью точного нахождения как положения центра масс , так и массы всего маятника.

Преобразуем уравнение (5) к виду с легко измеряемыми параметрами. Маятник представляет собой систему из двух жестко связанных тел: ненагруженного маятника Обербека с массой и однородного диска с массой (рис. 3).

Так как относительно центра масс векторная сумма моментов масс тел системы равна нулю, получаем:

.

Отсюда расстояние между осью вращения и центром масс полученного маятника равно:

. (6)

Подставим (6) в (5) и, учитывая, что , получаем расчетную формулу для экспериментально определения момента инерции испытываемого физического маятника:

. (7)

В формулах (6) и (7) #ris3">рис. 3). Диск однородный – его центр масс совпадает с геометрическим центром. Все величины в формуле (7) теперь достаточно легко измерить.

С другой стороны, момент инерции маятника можно рассчитать, если известен (относительно оси ) момент инерции ненагруженного маятника Обербека. Действительно, в силу свойства аддитивности момента инерции имеем:

,

где – момент инерции диска радиуса , рассчитанный по теореме Гюйгенса-Штейнера относительно оси ():

.

Таким образом, формула для расчета момента инерции испытываемого нами маятника принимает вид:

. (8)

1 Диск известной массы https://pandia.ru/text/80/230/images/image033_17.gif" width="11 height=23" height="23"> между осью вращения и центром диска получить у преподавателя.

2 Отклонив маятник на малый угол , возбудить его колебания. Измерить время десяти колебаний. Измерения повторить еще 2 раза и их результаты занести в таблицу.

Учреждение образования

кафедра математики и физики

МАЯТНИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ № 1.2

по дисциплине

«ФИЗИКА»

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

кафедра математики и физики

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО

МАЯТНИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №1.2

по дисциплине

«ФИЗИКА»

для студентов всех специальностей

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО

МАЯТНИКА

ЦЕЛЬ РАБОТЫ: определить момент инерции физического маятника и исследовать зависимость момента инерции от положения центра масс маятника относительно оси вращения.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: физический маятник на кронштейне, секундомер, призма на подставке, масштабная линейка.

ЭЛЕМЕНТЫ ТЕОРИИ

Периодические смещения тела относительно некоторого устойчивого положения (положения равновесия) называют колебательным движением или простыми колебаниями . Колебательные движения в общем случае представляют собой сложные физические процессы. Учение о колебаниях служит основой целого ряда прикладных дисциплин (акустика, теория машин, сейсмология и др.).

Простейшим видом колебаний является гармоническое колебательное движение. Гармонические колебания тела возникают при действии на него силы, пропорциональной смещению, т.е. . Эту силу называют возвращающей. Природа возвращающей силы может быть различна (сила упругости, сила тяжести и др.) При гармоническом движении зависимость пути (смещения ) от времени выражается функцией синуса или косинуса:

,

где ‑ максимальное смещение тела от положения равновесия (амплитуда),

‑ круговая или циклическая частота,

‑ время одного полного колебания (период),

‑ начальная фаза колебания.

Ускорение тела, совершающего гармонические колебания, пропорционально смещению и направлено всегда в сторону равновесия, т.е. для каждого момента времени смещение и ускорение имеют противоположные знаки:

. (1)

Гармонические колебания совершают маятники под действием силы тяжести, если углы отклонения от отвесного положения (положения равновесия) малы. Маятники бывают простые и сложные. Тело малых размеров (материальная точка), подвешенное на длинной нити, растяжением и весом которой можно пренебречь, называют простым или математическим маятником . Твердое тело произвольной формы, укрепленное на горизонтальной оси, не проходящей через центр тяжести, представляет собой сложный или физический маятник .

Всякое твердое тело можно рассматривать как совокупность неизменно соединенных материальных точек с массами
,
, . . .,
.

При отклонении физического маятника от положения равновесия на угол (рис.1) на каждый его элемент будет действовать момент силы тяжести относительно оси вращения . Сумма моментов всех этих сил равна моменту равнодействующей сил тяжести
, приложенной к центру тяжести маятника (точки ).

Под действием момента силы тяжести маятник приходит в колебательное движение с угловым ускорением
.

Если обозначить расстояние от оси вращения до центра тяжести через , то момент силы тяжести
выразится так:

или при малых углах

, (2)

где ‑ плечо силы
,

‑ масса маятника,

‑ ускорение свободного падения тела в данном месте.

При колебаниях маятника центр его тяжести движется по дуге круга, поэтому уравнение второго закона Ньютона для вращательного движения применимо и для маятника. Оно запишется в виде:

, (3)

где ‑ момент инерции тела относительно оси вращения.

Моментом инерции материальной точки называют произведение массы (
)на квадрат расстояния () от оси вращения до нее (
). Момент инерции тела равен сумме моментов инерции его частиц относительно этой же оси, то есть

.

Подставив в уравнение (3) значение
и решив его относительно углового ускорения, получим

, (4)

Уравнение (4) отличается от уравнения (1) только тем, что в него входят угловые величины вместо линейных.

Из сравнения уравнений (1) и (4) следует, что
или
, откуда получается формула для периода колебаний физического маятника:

. (5)

Из формулы периода колебаний физического маятника (5) найдем его момент инерции:

, (6)

где
‑ период колебаний маятника.

Это выражение является расчетной формулой для определения момента инерции физического маятника.

МЕТОДИКА ЭКСПЕРИМЕНТА И ОПИСАНИЕ УСТАНОВКИ

Физический маятник в данной работе состоит из стального стержня

ОD, на котором винтами крепится массивное тело В цилиндрической формы (рис.2). При освобождении опорных винтов, тело В можно перемещать по стержню и, следовательно, изменять положение центра тяжести маятника.

Для подвеса маятника служит специальный кронштейн, на который подвешивается маятник в точке .

Для нахождения центра тяжести маятника (точка ) служит специальная призма, укрепленная на устойчивой подставке. Маятник кладется горизонтально на ребро этой призмы и, наблюдая за балансированием, отыскивается такое положение, при котором моменты сил тяжести, действующие на правую и левую части маятника, окажутся равными (рис.3). При таком положении центр тяжести маятника будет расположен в стержне против точки опоры. Расстояние
определяется при помощи масштабной линейки.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

и т.д. для , и r 3.

Зависимость от изображают графически в выбранной системе координат, причем на горизонтальной оси откладывают величину (м ), а на вертикальной (кг  м 2 ).

КОНТРОЛЬНЫЕ ВОПРОСЫ

Определение физического маятника.

Определение момента инерции материальной точки и момента инерции тела.

Дать 2 определения момента силы (через расстояние от центра тяжести до оси вращения и через плечо силы).

Записать II закон динамики для движения маятника и вывести рабочую формулу для периода колебаний физического маятника.

На ось маятника намотать нить подвески и зафиксировать ее.

Проверить, отвечает ли нижняя грань кольца нулю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту. Привинтить верхний кронштейн.

Нажать кнопку «ПУСК» миллисекундомера (сотового телефона).

В момент прохождения маятником нижней точки остановить миллисекундомер.

Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно, один виток рядом с другим.

Фиксировать маятник, обращая внимание на то, чтобы нить в этом положении не была слишком скручена.

Записать измеренное значение времени падения маятника.

Определить замер времени n = 10 раз.

Определить значение среднего времени падения маятника по формуле:

где n – количество выполненных замеров, t i – значение времени, полученное в i – том замере, t – среднее значение времени падения маятника.

По шкале на вертикальной колонке прибора определить расстояние, проходимое маятником за время падения.

Используя формулу (11) и известные значения диаметров d о и d н , определить диаметр оси вместе с намотанной на нее нитью.

По формуле (10) вычислить массу маятника вместе с кольцом, наложенным в данном опыте. Значения масс отдельных элементов нанесены на них.

По формуле (9) определить момент инерции маятника.

Сравнить с теоретическим значением момента инерции

I теор = I о + I м,

где I о – момент инерции оси, I м - момент инерции маховика, которые вычисляются по следующим формулам:

I о = m o r o 2 / 2 ; I к = m м r м 2 / 2 .

Практические данные:

Длина маятника.

Таблица 1.

Подставив все и вычислив получим:

I 1 =(0.00090±0.00001) кг*м 2 .

Вывод: В ходе работы были определены моменты инерции маятника для разных длин намотанной нити и определены погрешности. Сравнение результатов расчётов и экспериментальное значение обнаруживает значительное различие данных.

Вывод: Мы определили экспериментальный и теоретический моменты инерции маятника, которые составили

и сравнили их

1.1. Движение маятника Максвелла представляет собой пример плоского движения твердого тела, при котором траектории всех его точек лежат в параллельных плоскостях. Это движение может быть сведено к поступательному движению маятника и вращательному движению вокруг оси, проходящей через его центр масс перпендикулярно этим плоскостям.

Такой тип движения широко распространен в технике: качение цилиндра по плоскости, колеса автомобиля, катка дорожной машины, движение вращающегося винта вертолета и т. д.

1.2. Целью настоящей лабораторной работы является экспериментальное ознакомление с плоским движением твердого тела на примере маятника Максвелла и определение момента инерции маятника.

2. ОСНОВНЫЕ ПОНЯТИЯ

2.1. Маятник Максвелла представляет собой небольшой маховик. Он может опускаться под действием силы тяжести и силы натяжения нитей, предварительно намотанных на ось маятника (рис.1). Нити во время движения вниз разматываются полностью. Раскрутившийся маховик продолжает вращаться в том же направлении и наматывает нити на ось, вследствие чего поднимается вверх, замедляя при этом свое движение. Дойдя до верхней точки -опять начинает опускаться вниз.

Маховик совершает периодически повторяющееся движение, поэтому он получил название маятника. Итак, движение маятника Максвелла можно разделить на две стадии: опускание и подъем.

2.2. Согласно основным законам динамики поступательного и вращательного движения (для соответственных осей), пренебрегая силами трения о воздух и отклонением нитей от вертикали, запишем

где m - масса маятника, I - момент инерции маятника относительно оси, - радиус оси маятника, N - сила натяжения каждой нити, g - ускорение свободного падения, a - линейное ускорение центра масс маятника, - угловое ускорение. Вследствие нерастяжимости нитей

Эти уравнения применимы как к первой, так и ко второй стадиям движения маятника. Начальные условия на разных стадиях различны: при опускании маятника начальная скорость его центра масс равна нулю, при его подъеме она отлична от нуля.

2.3.Из уравнений (1), (2), (3) следует

(5)

Из зависимости пути от времени при равноускоренном движении с нулевой начальной скоростью можно найти линейное ускорение маятника

где t - время движения маятника от верхней до нижней точки, h - расстояние, проходимое за это время. При имеем ; (7)

Отметим, что направления линейного ускорения и сил натяжения не зависят от того, куда движется маятник - вверх или вниз. За одно полное колебание линейная скорость меняет своё направление в нижней точке на противоположное, а линейное ускорение и силы не меняют. Угловая же скорость, наоборот, не меняет своего направления, а момент сил и угловое ускорение в нижней точке меняют на противоположные.

2.4.При подъеме вверх маятник движется равнозамедленно. Высота h2 , на которую он поднимется, будет меньше, чем та, с которой опускается h1 . Разность этих высот определяет убыль механической энергии, затраченной на преодоление сил деформации нитей при ударе и сил сопротивления движению.

Доля потерянной механической энергии

(9)

ОПИСАНИЕ УСТАНОВКИ

3.1. Схема установки изображена на рис. 2. В основании 1 закреплена колонка 2, на ней держится верхний кронштейн 3, на котором находится электромагнит 4, фотоэлектрический датчик 5 и вороток 6 для выравнивания подвески маятника. К нижнему кронштейну прикреплен второй фотоэлектрический датчик 7. Маховик маятника Максвелла состоит из диска 8, насаженного на ось 9, и прикреплённого к нему массивного кольца 10. Он подвешен на двух параллельных нитях, намотанных на ось. Маятник удерживается в верхнем положении электромагнитом. Высоты опускания и подъёма маятника определяются по миллиметровой линейке 11, находящейся на колонке прибора. Миллисекундомер МС 12 предназначен для измерения времени t движения маятника Максвелла. Начало и окончание отсчёта времени осуществляются автоматически с помощью фотодатчиков, упомянутых выше.

Определение момента инерции маятника Максвелла производится косвенным образом.

Из уравнений (6) и (8) следует, что момент инерции можно рассчитать по формуле

Здесь m – полная масса маятника,

m = m о + m д + m K , (11)

где m о - масса оси, m д - масса диска,.

4. ПОРЯДОК ИЗМЕРЕНИЙ

4.1. Технические данные.

4.1.1. Внести данные установки в табл. 1.

Таблица 1

4.1.2. Занести в табл. 2 значения масс и диаметров элементов маятника. Эти данные указаны на установке.

Таблица 2

4.3. Определение момента инерции маятника Максвелла.

4.2.2. На ось маятника симметрично, виток к витку, намотать нити подвески и зафиксировать маятник. Работать следует очень аккуратно.

4.2.3. Отпустить маятник и запустить отсчёт времени. В нижней точке отсчёт остановить.

4.2.5. Измеренное значение времени движения маятника занести в табл.3. Повторяя операции по пунктам 4.2.2 и 4.2.3, провести измерение времени еще 10 раз и данные занести в табл. 3.

Таблица 3

4.3. Определение убыли механической энергии

4.3.1. По линейке определить высоту h 1 , с которой опускается маятник; занести в табл. 3.

4.3.2. Повторить операции, описанные в п. 4.2.2 и 4.2.3, дать маятнику совершить пять полных колебаний, измерить разность высот d h . Это измерение произвести 1 раз и занести его результат в табл. 3.

5. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

5.1. Определение момента инерции маятника Максвелла.

Вычислить среднее значение времени движения маятника и занести в табл. 3.

Вычислить среднюю квадратичную ошибку в измерении времени движения маятника

(12)

5.1.3. Вычислить абсолютную случайную ошибку

D t сл = 2,1 DS . (13)

5.1.4. Вычислить полную абсолютную ошибку

D t = D t сл + D t приб. (14)

5.1.5. Вычислить относительную ошибку

все вычисленные величины поместить в табл. 3.

5.1.6. По формуле (10) вычислить момент инерции маятника, подставляя в качестве его среднее значение.

5.1.7. Вычислить относительную ошибку момента инерции маятника

, (16)

где D m , D rо , D h1 - приборные погрешности соответственных величин, Dt – полная абсолютнаяпогрешность времени движения; m - суммарная масса маятника, вычисленная по формуле (11).

5.1.8. По полученному значению e J рассчитать величину абсолютной ошибки DJ в определении момента инерции

DJ = e J ·J = . (17)

Округлить DJ до одной значащей цифры, а значения `J до разряда абсолютной ошибки.

5.1.9. Окончательный результат записать в виде

J =`J ± D J = (±) кг × м 2 . (18)

5.2. Определение убыли механической энергии при движении маятника Максвелла.

5.2.1. Формула (9) выражает долю механической энергии, потерянной за пять колебаний маятника Максвелла; за одно колебание доля будет в пять раз меньше:

6. ВОПРОСЫ, выносимые на ЗАЩИТУ РАБОТЫ

1. Основной закон динамики поступательного движения.

3. Как изменяются импульс и осевой момент импульса маятника Максвелла в нижней точке его движения? Объясните причины.

4. Закон сохранения полной энергии для маятника Максвелла.

5. Найти линейную и угловую скорости маятника в нижней точке.

6. Момент инерции твердого тела (определение). От чего зависит его величина?

7. Найти отношение кинетической энергии поступательного движения к кинетической энергии вращательного движения для данного маятника Максвелла.

8. Как меняются линейное и угловое ускорения за период движения маятника Максвелла?

9. Импульс и осевой момент импульса твердого тела.

10. Оценить натяжение нитей при прохождении маятником нижней точки (продолжительность “удара” в ней принять равной Dt »0,05c).

11. Как изменится время движения маятника, если радиус его оси увеличить в два раза?

12. Кинетическая энергия поступательного и вращательного движения твердого тела.

13. Расчет момента инерции диска радиусом R , массой m

14. Какие силы и моменты сил действуют на маятник Максвелла при его движении? Как они изменяются за период?

15. Расчет момента инерции кольца радиусом R , массой m относительно оси, проходящей через центр перпендикулярно его плоскости.

16. Получить формулу (10), исходя из закона сохранения механической энергии. (Учесть, что для маятника Максвелла Е к вр >>Е к пост ).

17. На каком участке движения маятника, верхнем или нижнем, потери механической энергии больше? Объяснить причины.