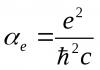1. Ван – дер – Ваальсова химическая связь характерна для электрически нейтральных атомов, не имеющих электрического дипольного момента.

Силу притяжения называют дисперсионной.

Для полярных систем с постоянным дипольным моментом, преобладает ориентационный механизм химической связи Ван – дер – Ваальса.

Для молекул с высокой поляризацией характерен индуцированный электрический момент при сближении молекул на достаточно близкое расстояние. В общем случае могут возникать все три вида механизма химической связи Ван – дер – Ваальса, которая слабее всех остальных видов химической связи на два – три порядка.

Полная энергия взаимодействия молекул с химической связью Ван – дер – Ваальса, равна сумме энергий дисперсионного, ориентационного и индуцированного взаимодействий.

2. Ионная (гетерополярная) химическая связь возникает, если один атом способен передавать другому атому один или несколько электронов.

В результате возникают положительно и отрицательно заряженные ионы, между которыми устанавливается динамическое равновесие. Такая связь характерна для галоидов и щелочных металлов. Зависимость W p (r) для молекул с ионной связью приведена на рис. 8.1. Расстояние r 0 соответствует минимуму потенциальной энергии.

3. Ковалентная (гомеополярная) химическая связь или атомная связь возникает, когда взаимодействуют атомы с близкими свойствами.

При взаимодействии появляются состояния с повышенной плотностью электронного облака и появления обменной энергии.

В квантовой теории показано, что обменная энергия является следствием тождественности близко расположенных частиц.

Характерной особенностью атомной связи является ее насыщаемость, т. е. каждый атом способен образовать ограниченное число связей.

4. В металлической химической связи участвуют все атомы кристалла, и обобществленные электроны свободно перемещаются внутри всей решетки кристалла.

Молекула водорода

Молекулу водорода связывают силы, приводящие к этой связи, являются обменными, т. е. для рассмотрения требуется квантовый подход.

Используя теорию возмущений Гейтлер и Ф. Лондон в 1927 г. решили в приближенном варианте.

В квантовой механике задача о молекуле водорода сводится к решению уравнения Шредингера для стационарного состояния.

Используя адиабатическое приближение, т. е. рассмотрим волновую функцию как функцию только координат электронов, а не атомных ядер.

Полная волновая функция зависит не только от пространственных координат электронов, но и от их спинов и является антисимметричной.

Если учитывать только волновую функцию электрона задачу можно решить, если учесть 2 случая:

1. Спиновая волновая функция антисимметрична, а пространственная волновая функция – симметрична и суммарный спин двух электронов равен нулю (синглетное состояние).

2. Спиновая волновая функция симметрична, а пространственная волновая функция – антисимметрична и суммарный спин двух электронов равен единице и может ориентироваться тремя различными способами (триплетное состояние).

В симметричном состоянии, когда спиновая волновая функция антисимметрична и в нулевом приближении получается симметричная пространственная волновая функция с разделяющимися переменными.

В триплетном состоянии, когда спиновая волновая функция симметрична, получается антисимметричная пространственная волновая функция.

Из-за тождественности электронов, возникает обменное взаимодействие, которое проявляется в вычислениях из-за использования симметричной и антисимметричной пространственных волновых функций.

При сближении атомов в синглетном спиновом состоянии (спины антипараллельны) энергия взаимодействия сначала убывает, а затем быстро растет. В триплетном спиновом состоянии (спины параллельны) минимум энергии не возникает.

Равновесное положение атома существует только в синглетном спиновом состоянии, когда энергия обращается в минимум. Только в этом состоянии и возможно образование атома водорода.

Молекулярные спектры

Молекулярные спектры возникают в результате квантовых переходов между уровнями энергий W * и W ** молекул согласно соотношению

hn = W * - W ** , (1)

где hn - энергия испущенного или поглощаемого кванта частоты n.

Молекулярные спектры сложнее атомных спектров, что определяется внутренним движением в молекулах.

Так как, кроме движения электронов относительно двух и более ядер в молекуле, происходят колебательные движения ядер (вместе с окружающими их внутренними электронами) около положений равновесия и вращательных движений молекул.

Электронному, колебательному и вращательному движениям молекул соответствуют три типа уровней энергии:

W e , W кол и W вр,

и три типа молекулярных спектров.

Согласно квантовой механике энергии всех видов движений молекулы могут принимать только определенные значения (кроме энергии поступательного движения).

Энергия молекулы W, изменение которой определяет молекулярный спектр, может быть представлена в виде суммы квантовых значений энергий:

W = W e + W кол + W вр, (2)

причем по порядку величины:

W e: W кол: W вр = 1: .

Следовательно,

W e >> W кол >> W вр.

DW = DW * - DW ** = DW e + DW кол + DW вр. (3)

Энергия электронов W e имеет порядок нескольких электронвольт:

W кол » 10 - 2 - 10 - 1 эВ, W вр » 10 - 5 - 10 - 3 эВ.

Система уровней энергии молекул характеризуется совокупностью далеко отстоящих друг от друга электронных уровней энергии.

Колебательные уровни расположены значительно ближе друг к другу, а вращательные уровни энергии располагаются еще ближе друг к другу.

Типичные молекулярные спектры - совокупности узких полос (состоящие из большого числа отдельных линий) различной ширины в УФ, видимой и ИК области спектра, четкие с одного края и размытые с другого .

Энергетические уровни а и б соответствуют равновесным конфигурациям 2-х молекул (рис. 2).

Каждому электронному состоянию соответствует определенное значение энергии W e - наименьшее значение, основного электронного состояния (основной электронный уровень энергии молекулы).

Набор электронных состояний молекулы определяется свойствами ее электронной оболочки.

Колебательные уровни энергии

Колебательные уровни энергии можно найти квантованием колебательного движения, которое приближенно считают гармоническим.

Двухатомную молекулу (одна колебательная степень свободы, соответствующая изменению межъядерного расстояния r) можно рассматривать как гармонический осциллятор, квантование которого дает равноотстоящие уровни энергии:

, (4)

где n - основная частота гармонических колебаний молекулы;

v кол = 0, 1, 2, ... - колебательное квантовое число.

Вращательные уровни энергии

Вращательные уровни энергии можно найти квантованием вращательного движения молекулы, рассматривая ее как твердое тело с определенным моментом инерции I.

В случае двухатомной или линейной трехатомной молекулы ее энергия вращения

где I - момент инерции молекулы относительно оси, перпендикулярной оси молекулы; L - момент импульса.

Согласно правилам квантования

, (6)

где J = 0, 1, 2, 3, ... - вращательное квантовое число.

Для вращательной энергии получаем

, (7)

Вращательная постоянная, определяет масштаб расстояния между уровнями энергии.

Многообразие молекулярных спектров обусловлено различием типов переходов между уровнями энергии молекул.

Основная задача теорий химической кинетики - предложить способ расчета константы скорости элементарной реакции и ее зависимости от температуры, используя различные представления о строении реагентов и пути реакции. Мы рассмотрим две простейшие теории кинетики - теорию активных столкновений (ТАС) и теорию активированного комплекса (ТАК).

Теория активных столкновений основана на подсчете числа столкновений между реагирующими частицами, которые представляются в виде твердых сфер. Предполагается, что столкновение приведет к реакции, если выполняются два условия: 1) поступательная энергия частиц превышает энергию активации E A ; 2) частицы правильно ориентированы в пространстве относительно друг друга. Первое условие вводит в выражение для константы скорости множитель exp(-E A /RT ), который равен доле активных столкновений в общем числе столкновений. Второе условие дает так называемый стерический множитель P - константу, характерную для данной реакции.

В ТАС получены два основных выражения для константы скорости бимолекулярной реакции. Для реакции между разными молекулами (A + B продукты) константа скорости равна

Здесь N A - постоянная Авогадро, r - радиусы молекул, M - молярные массы веществ. Множитель в больших круглых скобках - это средняя скорость относительного движения частиц A и B.

Константа скорости бимолекулярной реакции между одинаковыми молекулами (2A продукты) равна:

(9.2)

Из (9.1) и (9.2) следует, что температурная зависимость константы скорости имеет вид:

.

Согласно ТАС, предэкспоненциальный множитель слабо зависит от температуры. Опытная энергия активации E оп, определяемая по уравнению (4.4), связана с аррениусовской, или истинной энергией активации E A соотношением:

E оп = E A - RT /2.

Мономолекулярные реакции в рамках ТАС описывают с помощью схемы Линдемана (см. задачу 6.4), в которой константу скорости активации k 1 рассчитывают по формулам (9.1) и (9.2).

В теории активированного комплекса элементарную реакцию представляют как мономолекулярный распад активированного комплекса по схеме:

Предполагается, что между реагентами и активированным комплексом существует квазиравновесие. Константу скорости мономолекулярного распада рассчитывают методами статистической термодинамики, представляя распад как одномерное поступательное движение комплекса по координате реакции.

Основное уравнение теории активированного комплекса имеет вид:

, (9.3)

где k B = 1.38 . 10 -23 Дж/К - постоянная Больцмана, h = 6.63 . 10 -34 Дж. с - постоянная Планка, - константа равновесия образования активированного комплекса, выраженная через молярные концентрации (в моль/л). В зависимости от того, как оценивают константу равновесия, различают статистический и термодинамический аспекты ТАК.

В статистическом подходе константу равновесия выражают через суммы по состояниям:

, (9.4)

где - полная сумма по состояниям активированного комплекса, Q реаг - произведение полных сумм по состояниям реагентов, - энергия активации при абсолютном нуле, T = 0.

Полные суммы по состояниям обычно разлагают на сомножители, соответствующие отдельным видам движения молекул: поступательному, электронному, вращательному и колебательному:

Q = Q пост. Q эл. . Q вр. . Q кол.

Поступательная сумма по состояниям для частицы массой m равна:

Q пост = .

Эта поступательная сумма имеет размерность (объем) -1 , т.к. через нее выражаются концентрации веществ.

Электронная сумма по состояниям при обычных температурах, как правило, постоянна и равна вырожденности основного электронного состояния: Q эл = g 0 .

Вращательная сумма по состояниям для двухатомной молекулы равна:

Q вр = ,

где m = m 1 m 2 / (m 1 +m 2) - приведенная масса молекулы, r - межъядерное расстояние, s = 1 для несимметричных молекул AB и s =2 для симметричных молекул A 2 . Для линейных многоатомных молекул вращательная сумма по состояниям пропорциональна T , а для нелинейных молекул - T 3/2 . При обычных температурах вращательные суммы по состояниям имеют порядок 10 1 -10 2 .

Колебательная сумма по состояниям молекулы записывается как произведение сомножителей, каждый из которых соответствует определенному колебанию:

Q кол = ,

где n - число колебаний (для линейной молекулы, состоящей из N атомов, n = 3N -5, для нелинейной молекулы n = 3N -6), c = 3 . 10 10 см/с - скорость света, n i - частоты колебаний, выраженные в см -1 . При обычных температурах колебательные суммы по состояниям очень близки к 1 и заметно отличаются от нее только при условии: T > n . При очень высоких температурах колебательная сумма для каждого колебания прямо пропорциональна температуре:

Q i .

Отличие активированного комплекса от обычных молекул состоит в том, что он имеет на одну колебательную степень свободы меньше, а именно: то колебание, которое приводит к распаду комплекса, не учитывается в колебательной сумме по состояниям.

В термодинамическом подходе константу равновесия выражают через разность термодинамических функций активированного комплекса и исходных веществ. Для этого константу равновесия, выраженную через концентрации, переводят в константу, выраженную через давления. Последняя константа, как известно, связана с изменением энергии Гиббса в реакции образования активированного комплекса:

.

Для мономолекулярной реакции, в которой образование активированного комплекса происходит без изменения числа частиц, = и константа скорости выражается следующим образом:

Энтропийный множитель exp (S /R ) иногда интерпретируют как стерический множитель P из теории активных столкновений.

Для бимолекулярной реакции, протекающей в газовой фазе, в эту формулу добавляется множитель RT / P 0 (где P 0 = 1 атм = 101.3 кПа), который нужен для перехода от к :

Для бимолекулярной реакции в растворе константу равновесия выражают через энергию Гельмгольца образования активированного комплекса:

Пример 9-1. Константа скорости бимолекулярной реакции

2NO 2 2NO + O 2

при 627 К равна 1.81 . 10 3 см 3 /(моль. с). Вычислите истинную энергию активации и долю активных молекул, если диаметр молекулы NO 2 можно принять равным 3.55 А, а стерический множитель для этой реакции равен 0.019.

Решение. При расчете будем опираться на теорию активных столкновений (формула (9.2)):

.

Это число представляет собой долю активных молекул.

При расчетах констант скорости с использованием различных теорий химической кинетики необходимо очень аккуратно обращаться с размерностями. Обратите внимание на то, что радиус молекулы и средняя скорость выражены через см для того, чтобы получить константу в см 3 /(моль. с). Коэффициент 100 служит для перевода м/с в см/с.

Истинную энергию активации легко вычислить через долю активных молекул:

Дж/моль = 166.3 кДж/моль.

Пример 9-2. Используя теорию активированного комплекса, определите температурную зависимость константы скорости тримолекулярной реакции 2NO + Cl 2 = 2NOCl при температурах, близких к комнатной. Найдите связь между опытной и истинной энергиями активации.

Решение. Согласно статистическому вариант ТАК, константа скорости равна (формула (9.4)):

.

В суммах по состояниям активированного комплекса и реагентов мы не будем учитывать колебательные и электронные степени свободы, т.к. при низких температурах колебательные суммы по состояниям близки к единице, а электронные - постоянны.

Температурные зависимости сумм по состояниям с учетом поступательного и вращательного движений имеют вид:

Активированный комплекс (NO) 2 Cl 2 - нелинейная молекула, поэтому его вращательная сумма по состояниям пропорциональна T 3/2 .

Подставляя эти зависимости в выражение для константы скорости, находим:

Мы видим, что тримолекулярные реакции характеризуются довольно необычной зависимостью константы скорости от температуры. При определенных условиях константа скорости может даже убывать с ростом температуры за счет предэкспоненциального множителя!

Опытная энергия активации этой реакции равна:

.

Пример 9-3. Используя статистический вариант теории активированного комплекса, получите выражение для константы скорости мономолекулярной реакции.

Решение. Для мономолекулярной реакции

A AN продукты

константа скорости, согласно (9.4), имеет вид:

.

Активированный комплекс в мономолекулярной реакции представляет собой возбужденную молекулу реагента. Поступательные суммы реагента A и комплекса AN одинаковы (масса одинакова). Если предположить, что реакция происходит без электронного возбуждения, то и электронные суммы по состояниям одинаковы. Если предположить, что при возбуждении строение молекулы реагента изменяется не очень сильно, то вращательные и колебательные суммы по состояниям реагента и комплекса почти одинаковы за одним исключением: активированный комплекс имеет на одно колебание меньше, чем реагент. Следовательно, колебание, приводящее к разрыву связи, учитывается в сумме по состояниям реагента и не учитывается в сумме по состояниям активированного комплекса.

Проводя сокращение одинаковых сумм по состояниям, находим константу скорости мономолекулярной реакции:

где n - частота колебания, которое приводит к реакции. Скорость света c - это множитель, который используют, если частота колебания выражена в см -1 . При низких температурах колебательная сумма по состояниям равна 1:

.

При высоких температурах экспоненту в колебательной сумме по состояниям можно разложить в ряд: exp(-x ) ~ 1 - x :

.

Этот случай соответствует ситуации, когда при высоких температурах каждое колебание приводит к реакции.

Пример 9-4. Определите температурную зависимость константы скорости для реакции молекулярного водорода с атомарным кислородом:

H 2 + O . HO . + H . (линейный активированный комплекс)

при низких и высоких температурах.

Решение. По теории активированного комплекса константа скорости для этой реакции имеет вид:

Будем считать, что электронные множители от температуры не зависят. Все поступательные суммы по состояниям пропорциональны T 3/2 , вращательные суммы по состояниям для линейных молекул пропорциональны T , колебательные суммы по состояниям при низких температурах равны 1, а при высоких температурах пропорциональны температуре в степени, равной числу колебательных степеней свободы (3N - 5 = 1 для молекулы H 2 и 3N - 6 = 3 для линейного активированного комплекса). Учитывая все это, находим, что при низких температурах

а при высоких температурах

Пример 9-5. Кислотно-основная реакция в буферном растворе протекает по механизму: A - + H + P. Зависимость константы скорости от температуры дается выражением

k = 2.05 . 10 13. e -8681/T (л. моль -1. с -1).

Найдите опытную энергию активации и энтропию активации при 30 о С.

Решение. Так как бимолекулярная реакция происходит в растворе, для расчета термодинамических функций используем выражение (9.7). В это выражение нужно ввести опытную энергию активации. Поскольку предэкспоненциальный множитель в (9.7) линейно зависит от T , то E оп = + RT . Заменяя в (9.7) на E оп, получим:

.

Отсюда следует, что опытная энергия активации равна E оп = 8681. R = 72140 Дж/моль. Энтропию активации можно найти из предэкспоненциального множителя:

,

откуда = 1.49 Дж/(моль. К).

9-1. Диаметр метильного радикала равен 3.8 А. Какова максимальная константа скорости (в л/(моль. с)) реакции рекомбинации метильных радикалов при 27 о С?(ответ)

9-2. Вычислите значение стерического множителя в реакции димеризации этилена

2C 2 H 4 C 4 H 8

при 300 К, если опытная энергия активации равна 146.4 кДж/моль, эффективный диаметр этилена равен 0.49 нм, а опытная константа скорости при этой температуре равна 1.08. 10 -14 см 3 /(моль. с).

9-7. Определите температурную зависимость константы скорости для реакции H . + Br 2 HBr + Br . (нелинейный активированный комплекс) при низких и высоких температурах.(ответ)

9-8. Для реакции CO + O 2 = CO 2 + O зависимость константы скорости от температуры при низких температурах имеет вид:

k(T ) ~ T -3/2. exp(-E 0 /RT )

(ответ)

9-9. Для реакции 2NO = (NO) 2 зависимость константы скорости от температуры при невысоких температурах имеет вид:

k(T ) ~ T -1 exp(-E 0 /RT )

Какую конфигурацию - линейную или нелинейную - имеет активированный комплекс?(ответ)

9-10. Используя теорию активного комплекса, вычислите истинную энергию активации E 0 для реакции

CH 3 . + C 2 H 6 CH 4 + C 2 H 5 .

при T = 300 K, если опытная энергия активации при этой температуре равна 8.3 ккал/моль.(ответ)

9-11. Выведите соотношение между опытной и истинной энергиями активации для реакции

9-12. Определите энергию активации мономолекулярной реакции при 1000 К, если частота колебаний по разрываемой связи равна n = 2.4 . 10 13 с -1 , а константа скорости равна k = 510 мин -1 .(ответ)

9-13. Константа скорости реакции первого порядка разложения бромэтана при 500 о С равна 7.3 . 10 10 с -1 . Оцените энтропию активации этой реакции, если энергия активации равна 55 кДж/моль. (ответ)

9-14. Разложение перекиси ди-трет -бутила в газовой фазе представляет собой реакцию первого порядка, константа скорости которой (в с -1) зависит от температуры следующим образом:

Используя теорию активированного комплекса, рассчитайте энтальпию и энтропию активации при температуре 200 о С. (ответ)

9-15. Изомеризация диизопропилового эфира в аллилацетон в газовой фазе представляет собой реакцию первого порядка, константа скорости которой (в с -1) зависит от температуры следующим образом:

Используя теорию активированного комплекса, рассчитайте энтальпию и энтропию активации при температуре 400 о С. (ответ)

9-16. Зависимость константы скорости разложения винилэтилового эфира

C 2 H 5 -O-CH=CH 2 C 2 H 4 + CH 3 CHO

от температуры имеет вид

k = 2.7. 10 11. e -10200/T (с -1).

Рассчитайте энтропию активации при 530 о С. (ответ)

9-17. В газовой фазе вещество А мономолекулярно превращается в вещество В. Константы скорости реакции при температурах 120 и 140 о С равны, соответственно, 1.806 . 10 -4 и 9.14 . 10 -4 с -1 . Рассчитайте среднюю энтропию и теплоту активации в этом температурном интервале.

Если не учитывать колебательные движения в молекуле углекислого газа, то средняя кинетическая энергия молекулы равна …

Решение: Средняя кинетическая энергия молекулы равна: , где – постоянная Больцмана, – термодинамическая температура; – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: . Для молекулы углекислого газа число степеней свободы поступательного движения , вращательного – , колебательного – , поэтому Следовательно, средняя кинетическая энергия молекулы равна: .

ЗАДАНИЕ N 2 Тема: Первое начало термодинамики. Работа при изопроцессах

На рисунке представлена диаграмма циклического процесса идеального одноатомного газа: За цикл газ получает количество теплоты (в ), равное …

Решение: Цикл состоит из изохорного нагревания (4–1), изобарного расширения (1–2), изохорного охлаждения (2–3) и изобарного сжатия (3–4). На первых двух этапах цикла газ получает теплоту. Согласно первому началу термодинамики, количество теплоты, получаемое газом, равно , где – изменение внутренней энергии, – работа газа. Тогда . Таким образом, количество теплоты, получаемое газом за цикл, равно

ЗАДАНИЕ N 3 Тема: Второе начало термодинамики. Энтропия

В ходе необратимого процесса при поступлении в неизолированную термодинамическую систему тепла для приращения энтропии верным будет соотношение …

Решение: Отношение в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией системы: . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах: . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса: .

Задание n 4 Тема: Распределения Максвелла и Больцмана

На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала: Для этой функции верными являются утверждения …

			положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы)
			при увеличении числа молекул площадь под кривой не изменяется
			с ростом температуры газа значение максимума функции увеличивается
			для газа с бόльшей молярной массой (при той же температуре) максимум функции расположен в области бόльших скоростей

Решение: Из определения функции распределения Максвелла следует, что выражение определяет долю молекул, скорости которых заключены в интервале скоростей от до (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости (при которой функция максимальна) следует, чтопрямо пропорциональна и обратно пропорциональна , где и – температура и молярная масса газа соответственно.

ЗАДАНИЕ N 5 Тема: Электростатическое поле в вакууме

На рисунках представлены графики зависимости напряженности поля для различных распределений заряда: График зависимости для шара радиуса R , равномерно заряженного по объему, показан на рисунке …

ЗАДАНИЕ N 6 Тема: Законы постоянного тока

На рисунке представлена зависимость плотности тока j , протекающего в проводниках 1 и 2, от напряженности электрического поля Е : Отношение удельных сопротивлений r 1 /r 2 этих проводников равно …

ЗАДАНИЕ N 7 Тема: Магнитостатика

Рамка с током с магнитным дипольным моментом , направление которого указано на рисунке, находится в однородном магнитном поле: Момент сил, действующих на магнитный диполь, направлен …

			перпендикулярно плоскости рисунка к нам
			перпендикулярно плоскости рисунка от нас
			по направлению вектора магнитной индукции
			противоположно вектору магнитной индукции

Реальный контур состоит из катушки индуктивности и конденсатора. Реальная катушка не может считаться только индуктивностью, которая накапливает магнитную энергию. Во-первых, провод обладает конечной проводимостью, во-вторых, между витками накапливается электрическая энергия, т.е. имеет место межвитковая ёмкость. То же самое можно сказать и о емкости. Реальная емкость помимо самой емкости будет иметь в своем составе индуктивности выводов и сопротивление потерь.

Для упрощения задачи рассмотрим модель реального колебательного контура с катушкой индуктивности состоящей всего из двух витков.

Эквивалентная схема будет иметь вид, приведённый на рисунке на рис. 4. ( и - индуктивность и сопротивление одного витка, - межвитковая ёмкость).

Однако, как показывает опыт радиоинженера, в большинстве случаев нет необходимости эту сложную схему.

Уравнение для электрической цепи, изображенной на рис. 5 получим на основе закона Кирхгофа. Используем второе правило: сумма падений напряжений на элементах контура равна алгебраической сумме внешних ЭДС, включенных в этот контур. В нашем случае ЭДС равна нулю, и получим:

Разделим слагаемые на и обозначим

Уравнение для идеального контура примет вид:

Имея модели двух динамических систем, можно уже сделать некоторые выводы.

Простое сравнение уравнений (В.6) и (В.9) показывает, что маятник при малых отклонениях и идеальный контур описываются одним и тем же уравнением, известным как уравнение гармонического осциллятора, которое в стандартной форме имеет вид:

Следовательно, и маятник, и контур как колебательные системы обладают одинаковыми свойствами. Это и есть проявление единства колебательных систем.

Имея эти модели, уравнения, их описывающие, и обобщая полученные результаты, дадим классификацию динамических систем по виду дифференциального уравнения. Системы бывают линейные и нелинейные.

Линейные системы описываются линейными уравнениями (см. (В.11) и (В.15)). Нелинейные системы описываются нелинейными уравнениями (например, уравнение математического маятника (В.9)).

Другим признаком классификации является число степеней свободы . Формальным признаком служит порядок дифференциального уравнения, описывающего движение в системе. Система с одной степенью свободы описывается уравнением 2-го порядка (или двумя уравнениями первого порядка); система с N степенями свободы описывается уравнением или системой уравнений порядка 2N.

В зависимости от того как изменяется энергия колебательного движения в системе, все системы делятся на два класса: консервативные системы – те, у которых энергия остаётся неизменной, и неконсервативные системы – те, у которых энергия изменяется с течением времени. В системе с потерями энергия убывает, однако возможны случаи, когда энергия возрастает. Такие системы называются активными.

Динамическая система может подвергаться и не подвергаться внешнему воздействию. В зависимости от этого различают четыре типа движения.

1.Собственные, или свободные колебания, системы. В этом случае от внешнего источника система получает конечный запас энергии и источник отключается. Движение системы при конечном начальном запасе энергии и представляет собственные колебания.

2.Вынужденные колебания. Система находится под действием внешнего периодического источника. Источник оказывает «силовое» воздействие, т.е. природа источника та же, что и у динамической системы (в механической системе – источник силы, в электрической – ЭДС и т.д.). Колебания обусловленные внешним источником, называются вынужденными. При отключении они исчезают.

3.Параметрические колебания наблюдаются в системах, у которых периодически во времени изменяется какой-либо параметр, например, ёмкость в контуре или длина маятника. Природа внешнего источника который, изменяет параметр, может отличаться от природы самой системы. Например, ёмкость можно изменять механически.

Нужно отметить, что строгое разделение вынужденных и параметрических колебаний возможно лишь для линейных систем.

4.Особый вид движения – автоколебания. Термин впервые введён академиком Андроновым. Автоколебание – это периодическое колебание, период, форма и амплитуда которого зависят от внутреннего состояния системы и не зависят от начальных условий. С энергетической точки зрения автоколебательные системы являются преобразователями энергии некоторого источника в энергию периодических колебаний.

Глава 1.СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЕ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР)

Уравнение такой системы имеет вид:

(примерами могут служить математический маятник при малых углах отклонения и идеальный колебательный контур). Решим уравнение (1.1) подробно, пользуясь классическим методом Эйлера. Ищем частное решение в виде:

где и – постоянные, пока неизвестные константы. Подставим (1.2) в уравнение (1.1)

Разделим обе части уравнения на и получим алгебраическое, так называемое характеристическое, уравнение:

Корни этого уравнения

где – мнимая единица. Корни мнимые и комплексно-сопряжённые.

Как известно, общее решение есть сумма частных, т.е.

Мы полагаем, что есть действительная величина. Чтобы это выполнялось, постоянные и должны быть комплексно сопряженными, т.е.

Две постоянные и определяются из двух начальных условий:

Решение в форме (1.8) преимущественно используется в теории; для прикладных задач оно не удобно, так как и не измеряются. Перейдём к форме решения, которое наиболее употребительно на практике. Представим комплексные постоянные в полярной форме:

Подставим их в (1.8) и воспользуемся формулой Эйлера

где - амплитуда колебаний, - начальная фаза.

И определяются из начальных условий. Заметим, что начальная фаза зависит от начала отсчёта во времени. Действительно, постоянную можно представить в виде:

Если начало отсчёта во времени совпадает с , начальная фаза равна нулю. Для гармонического колебания сдвиг по фазе и сдвиг во времени эквивалентны.

Разложим косинус в (1.13) на косинусоидальную и синусоидальную составляющие. Получим ещё одно представление:

Если и известны, то нетрудно найти амплитуду и фазу колебания, используя следующие соотношения:

Все три формы записи (1.8, 1.12, 1.15) эквивалентны. Использование конкретной формы определяется удобством рассмотрения конкретной задачи.

Анализируя решение, можно сказать , что собственные колебания гармонического осциллятора есть гармоническое колебание, частота которого зависит от параметров системы и не зависит от начальных условий; от начальных условий зависят амплитуда и начальная фаза.

Независимость от начальных условий частоты (периода) собственных колебаний называется изохорностью .

Рассмотрим энергию гармонического осциллятора на примере колебательного контура. Уравнение движения в контуре

Умножим слагаемые этого уравнения на :

После преобразования его можно представить в виде:

Найдем закон изменения энергии в конденсаторе. Ток в емкостной ветви можно найти используя следующее выражение

Подставив (1.28) в формулу для нахождения электрической энергии получим закон изменения электрической энергии на конденсаторе

Таким образом, энергия в каждом элементе контура колеблется с удвоенной частотой. График этих колебаний приведен на рис. 6.

В начальный момент времени вся энергия сосредоточена в емкости, магнитная энергия ровна нулю. По мере разряда емкости через индуктивность электрическая энергия из емкости переходит в магнитную энергию индуктивности. Через четверть периода вся энергия сосредотачивается в индуктивности, т.е. емкость полностью разрядилась. Затем этот процесс периодически повторяется.

Таким образом, колебание в идеальном контуре – это переход электрической энергии в магнитную и обратно, периодически повторяющийся во времени.

Этот вывод справедлив для любых электромагнитных колебательных систем, в частности для объемных резонаторов, где магнитная и электрическая энергия пространственно не разделены.

Обобщая этот результат, можно утверждать, что колебательный процесс в линейной консервативной системе – это периодический переход энергии одного типа в другой. Так, при колебаниях маятника кинетическая энергия переходит в потенциальную и наоборот.